多密钥全同态加密的研究现状与发展趋势

祁正华，何菲菲，张海桃，谭小辉

(南京邮电大学 计算机学院，江苏 南京 210023)

全同态加密（Fully Homomorphic Encryption，FHE）的思想源于“隐私同态”，由Rivest 等［1］在1978 年首次提出。 FHE 指在不解密的情况下对密态数据进行各种运算，其结果在解密后与对明文进行相应运算的结果是一样的（见图1）。 同态加密的本质是图1 所示的交换图表。 FHE 真正从根本上解决了将数据及操作委托给第三方时的保密问题。

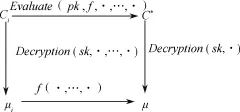
图1 同态加密交换图

随着Rainbow 和SIKE 相继被破解而双双陨落，基于格的密码学成为后量子时代抗量子密码的重要组成部分。 FHE 方案大多是以格上困难问题作为基础，从而FHE 也是后量子密码（Post-Quantum Cryptography，PQC）的组成之一。 目前，基于格的逐渐成为欧美国家在密码领域争夺的“战略制高点”，能够在大数据与云计算等新型服务模式下发挥重要作用［2］。

2009 年，由IBM 实验室的Gentry 构造了第一个真正意义的FHE 方案［3］，方案的设计是基于理想格（Ideal Lattice）上的有界编码问题（Bounded Distance Decoding Problem，BDDP）和稀疏子集和问题（Sparse Subset Sum Problem，SSSP）。

2011 年，Brakerski 等［4］提出BV 方案，首次利用容错学习（Learning with Errors，LWE）假设实现了FHE 并在Ring-LWE 假设下实现了FHE。 BV 方案采用重线性化技术和密钥交换技术降低了密文的噪声，优化了Gentry［3］提出的方案，但同时由于密钥交换技术需要在公钥生成阶段引入额外的信息，也因此使得BV 方案的存储开销增大。 2012 年，Brakerski 等［5］又提出了BGV 方案，该方案同样也使用了密钥交换技术，但不需要压缩解密电路，提高了算法的计算效率，同时也降低了方案的安全性假设。之后，Gentry 等［6］首次利用近似特征向量的方法，提出了密文形式为矩阵的FHE 方案（GSW 方案），且该方案未使用密钥交换技术，因此减少了存储开销，同时由于矩阵相乘不会改变维数，进而不会使得密文相乘的噪声大幅增加。 以上方案都是单密钥加密方案，不能满足不同密钥密文之间的运算，安全多方计算（n个参与方共同计算一个函数，计算完毕后每个参与方只知道自己的输入输出）在全同态加密方面得不到应用。

2012 年，López-Alt 等［7］提出了第一个多密钥全同态加密（MKFHE）方案，支持对不同用户（不同密钥）的密文进行任意的同态运算，且运算之后的结果由参与计算的所有用户联合解密，可以较好地解决多用户密文联合计算的问题。 该方案建立在一个与NTRU 相关的非标准假设上，但该方案的复杂度太高，且复杂度随着用户的增长呈指数增长。 2015年，Clear 等［8］基于GSW 方案［6］构造了一个MKFHE方案，方案的安全性可以规约到LWE 问题，该方案是第一个建立在标准假设上的多密钥全同态加密方案。 2016 年，Mukherjee 等［9］简化了Clear 等［8］的方案，同样是基于GSW 方案［6］、安全性归约到LWE问题假设，不同之处在于Mukherjee 等［9］扩展了方案的结构，使得扩展之后的方案可以进行一轮交互的分布式计算，但不足之处在于该方案只允许单跳运算。 为了解决这个问题，Peikert 等［10］构造了拥有多跳的MKFHE，不必提前获得参与方的信息，且与Mukherjee 等［9］构造的方案相比，方案生成的密文尺寸更短。 与此同时，Brakerski 等［11］同样基于GSW方案［6］设计出了多跳的MKFHE，它允许参与方动态的加入，可支持任意数量的运算以及多项式级别的参与方参与运算。 为提高多跳的MKFHE 的同态运算效率，荀艳梅等［12］基于Peikert 等［10］的MKFHE方案并结合密钥策略属性基全同态加密，构造了一个多跳多策略属性基全同态短密文加密方案，且该方案的密文扩展更容易实现。 2019 年，Li 等［13］基于BGV 方案［5］构造MKFHE 方案，方案对密文长度进行了缩减，提高了运算效率，同时也提出了一个直接解密协议，解除了计算密文只能由所有参与方的私钥解密的限制，但也只限于理论层面，还未投入到实际应用。 为了再次提高全同态加密方案的计算效率，同年，Chen 等［14］基于TFHE 方案提出了一个MKFHE 方案，首次对全同态加密进行了概念验证。

1 基本概念

1．1 符号说明

对于一个自然数n∈N，［n］ 表示｛1，2，…，n｝，⎿n」 表示小于n但最接近于n的整数，「n⏋表示大于n但最接近于n的整数，「n」表示对n四舍五入近似取整，Z 表示整数集，Zq表示模q剩余类。v［i］表示向量中的第i个元素，A［i，j］ 表示矩阵中第i行第j列的元素，［A ｜Ax］ 表示矩阵和向量的水平连接，〈a，b〉表示两个向量的内积。 对于分布B，x←B表示x从分布B中均匀取值。 对于向量x ＝（x1，x2，…，xn），lp范数是指，无穷范数是指‖x‖∞＝max（｜x1｜，｜x2｜，…，｜xn ｜），l1范数是指｜， 若无下标则记为2-范数。

令Φm（x） 为分圆多项式，则Rq ＝R／qR ＝Z（x）／〈Φm（x）〉 表示分圆多项式环，环中元素可表示为

1．2 相关定理

定理1容错学习问题（LWE）。 对于一个秘密向量上的LWE 分布As，χ指的是均匀选取，选取e←χ，输出（A，b ＝A·s ＋emodq）。

定理2判定性容错学习问题（DLWE）。 设为m个相互独立的采样，每个采样都是按照以下两种方式生成的：（1） 从中随机取样；（2） 从分布As，χ中取样。 DLWE 问题是指判定中的每个样本是从哪种方式中取样的。

定理3环上容错学习问题（RLWEΦ，q，χ）。 对于一个秘密向量s∈Rq，RLWE 分布Ls，χ是指定义为Rq ×Rq上按如下方式生成的概率分布，随机选取a∈Rq，e∈R服从概率分布χ，计算（a，b ＝a·s ＋e）。

定理4判定性容错学习问题（DRLWE）。 判断（a，b） 是从分布Ls，χ中采样还是从Rq × Rq中采样。

定理5DSPRΦ，q，χ问题是指难以区分以下两个多项式，一是多项式h ＝2g／f，其中f ＝2f′ ＋1 且在Rq上可逆，f′，g←χ；二是在上随机均匀采样得到多项式h。

定理6一个整数上的分布｛χn｝n∈N， 如果，称该分布是B －有界的，其中negl（λ） 是一个可忽略函数。

定理7设gT＝（1，2，22，…，2l－1） ∈Zl，l ＝「logq⏋，Gadget 矩阵G ＝In⊗gT∈Zn×nl，则对任意的，均存在一个随机有效的可计算函数G－1：同时x为关于参数O（1） 的亚高斯随机向量，且a ＝［Gx］q。 例如，若a ＝(7 1 5)T，有Gadget 矩阵

定理7 很容易扩展到矩阵上，如定理8 所示。

定理8设gT＝（1，2，22，…，2l－1） ∈Zl，l ＝「logq⏋，Gadget 矩阵G ＝In⊗gT∈Zn×nl，则对任意的， 均存在一个随机有效的可计算函数同时矩阵的任意行向量xi均为关于参数O（1） 的亚高斯随机向量，且AT＝［GXT］q。 例如，若Gadget 矩 阵G同 定 理 7， 存 在X ＝且AT＝［GXT］q，或A ＝［XGT］q。

1．3 关键技术

模交换技术（ModulusSwitch（） ）：模交换技术可以将模q下的密文c转换成较小的模p（p ＝qmod 2） 下密文c′，保证在同样私钥正确解密条件下，噪声规模减小p／q倍，即ModulusSwit ch（c，q，p）：输入c∈Rq和一个更小的模数p，输出的一个密文无限接近于c′ ＝（p／q）·c∈Rp且满足c′ ＝cmod 2。

密钥交换技术（SwitchKey（））：将对应的密文由（解密密钥为sk1） 转换成为密文（解密密钥为sk2）。

比特分解技术： 比特分解技术是指用BitDecomp（·） 和Powersof2（·） 这两个函数对数据进行比特位展开。 令l ＝「logq⏋， 则其具体表达分别为

BitDecomp（x∈，q）： 输入多项式x ＝（x1，x2，…，xn）和 模q， 输 出 （x1，0，x1，1，…，x1，l－1，…，xn，0，xn，1，…，xn，l－1） ∈｛0，1｝n－l， 其 中xi，j为xi进行二元比特分解之后的第j比特。

Powersof2（y∈，q）： 输入多项式y ＝（y1，输 出 （y1，2y1，…，2l－1y1，…，yn，

例如， 若x ＝（7，9），y ＝（2，6），l ＝4， 则BitDecomp（x，q）＝（1，1，1，0，1，0，0，1）。

自举（Bootstrapping）技术：当同态操作进行至噪声达到阈值而无法再进行操作时， 将此时的密文与对应私钥的密文进行同态解密的操作。 即将自己解密函数作为FHE．Eval算法中的输入函数，将达到噪声上限的密文与该密文解密秘钥中的每一位加密结果作为FHE．Eval算法中的输入密文，则执行FHE．Eval算法会生成一个与该密文对应相同明文的“新鲜”密文，从而可以继续进行密文同态运算。当密文再次达到噪声上限时，可以再进行一次同态解密运算，依次递归，在KDM 安全假设下，即可获得纯FHE 方案。 自举后可以得到支持继续同态操作的低噪声密文。 自举是目前最有效的消减密文噪声的操作，也是迄今为止实现全同态加密的唯一途径。

自举算法的形式化描述如下：

设加密方案中存在两对密钥对（pk1，sk1） 和（pk2，sk2）、 明文为μ， 则令c1为μ关于sk1的密文、表示用pk2逐比特加密sk1得到， 并将添加至加密方案的公钥中。 令解密电路为D， 自举算法执行流程如图2 所示。

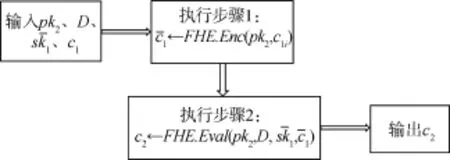
图2 自举算法执行流程图

1．4 格上困难问题

格是指n维空间Rn具有周期性结构的点的集合。

近似最短向量问题：定义格的任意一个格基B，近似因子γ ＝γ（n） ≥1，则近似最短向量问题是指找到一个非零格基向量B·x，使得对于任意的非零y，‖B·x‖≤γ（n）‖B·y‖成立。

近似最近向量问题：给定格的一个格基B、 目标向量t，找出一个格基向量B·x，使得对于任意的y，‖B·x － t‖≤γ‖B·y － t‖成立。

定义格Λ的逐次最小量为λ（Λ）＝inf｛r ｜表示以原点为球心、r为半径的闭球，span（Λ） 表示格Λ生成的线性空间。

最短线性无关向量问题：寻找格中n个线性无关向量v1，v2，…，vn， 使得对于任意的i∈［n］，‖vi‖≤γ·λi（Λ） 成立。

2 全同态加密及多密钥全同态加密

基于全同态加密的多密钥全同态加密的发展过程同全同态加密一样分为3 个阶段，下面分析各阶段的核心方法。

2．1 以Gentry 的突破性工作为基础

这一阶段全同态加密方案构造的思路是：首先构造一个部分（Somewhat）FHE 方案，即方案仅支持低多项式次数的密文同态计算。 然后，在稀疏子集和问题的假设下，通过“压缩解密电路”使方案变成“自举的”，从而通过迭代调用自举技术，对随着同态运算达到噪声阈值的新密文进行同态解密来约减噪声，使其允许至少再进行一次同态运算，最后在循环安全性假设（KDM）下获得真正意义上的FHE方案。

在同态运算过程中噪声的主要来源是同态乘法运算，其产生的噪声呈指数级别增长。 为解决噪声增长过快问题，需要将密文和密钥重新按位加密，之后再将得到的密文输入同态解密电路中，但这要求当同态运算电路深度大于解密电路深度时要通过压缩电路和逐比特加密降低噪声来实现全同态，这也限制了同态解密技术的使用。 由此可见，这一阶段仅实现单密钥全同态加密过程就十分复杂，因此，多密钥全同态加密不适合基于此阶段的方案进行构造。 此 阶 段 的 代 表 性 方 案 有 SV （ 10）［15］、SS（10）［16］、LMSV（11）［17］等。

2．2 基于LWE 和RLWE 的多密钥全同态加密方案

这一阶段全同态加密方案的构造思路是先构造一个层次型的同态加密方案，再通过一定的技术手段达到无限运算。 层次型的加密方案在进行同态乘法运算时同样会使得噪声呈指数级别的增长，例如，n维的数据进行一次同态乘法之后会产生n2维的噪声，两次同态乘之后会产生n4维的噪声，因此需要对噪声做一定的处理才能达到全同态。 2012 年Brakerski 等［5］提出了用密钥交换技术来解决维数膨胀问题，用模交换技术控制噪声从而使其达到全同态，在一定程度上摆脱了对自举的依赖，但最终要实现无限次的运算还需要自举技术。 此阶段出现的方案有Bra（12）［18］、BV（14）［19］等。

以这一阶段的方案作为基础方案构造的多密钥全同态加密方案可分为NTRU 型和BGV 型两大类。NTRU 型的MKFHE 是最早被提出的，BGV 型的MKFHE 是最晚被提出的。

2.2.1 NTRU 型MKFHE 的构造及优化

作为首个被提出的多密钥加密方案类型，对后来MKFHE 的构造起着至关重要的作用，NTRU 型多密钥加密方案［7］的基本构造过程如下。

（1） 初始化NTRU．Setup（1λ）： 安全参数为λ，选择整数n ＝n（λ）， 定义分圆多项式环R ＝Z（x）／xn ＋1， 其中xn ＋1 为2 的幂次阶分圆多项式，n为2 的幂次。 定义多项式环Rq ＝R／qR，R中上界为B ＝B（λ） 的错误分布χ。 定义一系列递减的模数q0＞q1＞…＞qL，令B≪qL，i∈｛0，1，2，…，L｝。

（2） 密钥生成NTRU．KeyGen（1n，1L）： 产生公钥、私钥和同态计算密钥，其中L为运算深度。

（3） 加密NTRU．Enc（pk，μ）： 将明文数据加密为c ＝hs ＋e ＋μ的形式，其中h为公钥，s，e←χ。

（4） 同态运算NTRU．Eval（c1，c2）：此阶段需要计算密钥的参与，用计算密钥结合模交换技术或密钥交换技术进行同态运算。

（5） 解 密NTRU．Dec（sk1，sk2，…，skn，c∗）： 其中c∗为经过同态计算产生的新鲜密文。

其安全性基于DSPRΦ，q，χ和RLWEΦ，q，χ问题。

当前对NTRU 型MKFHE 的优化主要是抑制噪声的增长速度、优化方案的安全性或在同态计算时减少计算密钥的交换次数甚至消除计算密钥的交换等。 李瑞 琪 等［20］便 利 用 工 具 向 量（g ＝（1，ω，其中ω为基，lq ＝「logωq⏋） 和比特分解技术构造了一个同态运算过程不需要计算密钥的层次型的NTRU 型MKFHE，提高了方案的运算效率，构造的方案相比原方案密钥的生成方式没有改变，只是在加密过程中先对“0”进行加密，其具体的优化过程如下。

RNTRU．Enc（pk，μ）：随机抽取lq组si，ei←χ用于计算NTRU．Enc（h，0） 来得到lq个“0 的密文”，然后将lq个0 的密文组成一个向量，最后输出密文

RNTRU．Dec（sk，c）：用联合私钥Fk ＝f1f2…fn（其中，为用户i的私钥） 进行解密，可得明文μ ＝NTRU．Dec（Fk，c［1］）。

此时对进行同态运算之后的密文进行解密便可不再需要计算密钥，直接用私钥与密文做内积即可得到明文。 下面以解密同态乘（cMult ＝c1g－1（c2） ∈为例进行论证，使用f＾＝f1·f2解密cMult时需计算f＾·cMult［1］，因此可令g－1c2得到的矩阵为可得

已知f ＝pf′ ＋1，f′←χ，因此可得f1≡1 modp、f2≡1 modp，又知g［1］＝1、c1，0［1］、c2，0［1］ 是“0”的密 文，因 此f1·c1，0［1］modp ＝0，f2·c2，0［1］modp ＝0，所以可得f＾·cMult［1］modp ＝μ1μ2，因此同态乘法运算过程不需要计算密钥的参与得证，同态加法运算过程同理。

除直接对同态运算过程优化外，还可采用间接方式。 例如，车小亮等［21］通过改变NTRU 型加密方案的底层结构对其安全性和效率进行了优化，将现有方案底层的分圆多项式环扩展到素数次分圆多项式环上，可以抵御更多的子域攻击。 然后通过扩展密文维度消除密钥交换技术，并结合模交换技术构造一个高效的层级的NTRU 型MKFHE。 其具体的优化过程如下。

对安全性的优化：只是将原方案中的分圆多项式用素数次分圆多项式替代，其他多项式时间算法不变。 定义素数次分圆多项式环为R ＝参数n和q ＝q（λ） 为素整数。 根据文献［22］可知，素数次分圆多项式可以抵抗更多的子域攻击。

对效率的优化：上面对安全性的优化只是改变了底层结构，并没有改变同态运算的结构，仍需要密钥交换来完成全同态，且产生的噪声同时受第i层和第i ＋1 层联合解密私钥的影响，导致噪声增长过快。 因此，车小亮等［21］又通过将明文μ转化为向量的形式μ′ ＝（μ，2μ，…，2l－1μ） 扩展密文多项式，并结合比特分解技术，优化NTRU 型多密钥同态运算结构，以消除同态运算过程中的密钥交换操作。NTRU 型MKFHE［7］最初的加密方案与车小亮等［21］所提优化后的方案对比如表1 所示。

表1 原方案与优化后的方案对比表

表1 从密文形式、同态加法和同态乘法3 方面进行对比分析。 从表1 中可以看出二者有两方面的区别，一方面是在密文形式方面的唯一区别：明文是否为向量；另一方面是由于优化的方案引入了比特分解技术，因此同态计算过程中省去了密钥交换，从而也使得同态计算过程更加简便高效。

此外，由于层级的加密方案每层密文维数不同，车小亮等［21］又提出了去尾函数来统一维数。 去尾函数表示去掉向量的li＋1→li项，使li维向量转换成li＋1维向量至此一个可以抵御更多子域攻击、不需要密钥交换的NTRU 型全同态加密被构造完成。

原始的NTRU 型解密是在解密之前先进行密钥交换，再用联合私钥与密文做内积，导致解密噪声较大。 车小亮等［23］便从方案的解密结构入手，设计了两种解密结构来降低解密噪声，一种是降低多项式系数来降低噪声，另外一种是通过扩展密文维度消除密钥交换的过程。 第一种优化的解密形式为（2／q）Fkc ＝μ ＋Error，但这种解密形式依然需要密钥交换；第二种优化的解密形式为Fk（c）＝μ ＋Error，其中c：＝Powersof2（μ）＋hs ＋2e，这一优化需要在解密之前对密文进行比特分解转换。 以同态乘法为例则：cMult＝ BitDecomp（c1）·c2， 设c2）。

2.2.2 BGV 型MKFHE 的构造及优化

BGV 型的多密钥全同态加密方案的密文结构相对比较特殊，密文扩展过程不需要计算密钥的加入，但当前对BGV 型MKFHE［24］的研究还很缺乏。其基本构造流程如下。

（1） 初始化BGV．SetUp（1λ，1L）： 在NTRU 型MKFHE 初始化的基础上增加了电路深度L。

（2） 密钥生成BGV．KeyGen（1n，1L）： 产生公私钥以及生成计算密钥所需的相关密文ems。

（3） 加密BGV．Enc（pk，μ）： 加密形式为c ＝其中

（4） 解密BGV．Dec（sk，c）： 解密形式为μ←modqlmodp， 其中表示用户的私钥合集，cs表示用户集合s的密文。

（5） 密文扩展BGV．Extand（ct，S′）： 输出新鲜密文其中密文组待扩展用户集S′ ＝｛j1，…，jk′｝（s∈s′）。 密文扩展的具体步骤为将cs划分为k个子向量cs ＝（ci，1｜ci，2｜…｜ci，k） ∈，此外令其对应的用户集为S′，如果用户集S′中的用户j也在用户集S中，则令否则

由于BGV 型MKFHE 通常有较大的密钥量且计算密钥的生成过程较为复杂，因此，对该类型多密钥全同态加密方案的优化主要是减少密钥量或简化计算密钥的生成过程。 2019 年，Li等［13］首先通过构造了一个嵌套型的BGV 密文和一个可分离的GSW 扩展密文使扩展密文的尺寸缩小一半， 然后将RBGV 密文和RGSW 密文的混合同态乘法应用于计算密钥的生成过程，以此来减少密文的输入输出，提高运算效率。 优化方案的初始化函数、密钥生成函数、加密函数都同原始的BGV 型函数同理，优化的部分为计算密钥的生成以及解密部分，具体的优化的步骤如下所示。

计算密钥的生成：分为生成扩展密文RBGV、生成扩展密文RGSW 和生成计算密钥3 部分。

（1） 生成扩展密文RBGV．Extand（）： 算法同BGV．Extand（） 一样，只不过原始BGV 型在密文扩展时将密文cs划分为了k个子向量，而本方案中将cs划分为了k ＋1 个子向量。

（2） 生 成 扩 展 密 文RGSW．Extand（）： 与GSW．Extand（） 的一般构造算法的不同之处是密钥生成函数及本方案新加入了一个多项式时间算法EncRand（r，P）。 本方案中私钥sk ＝（1，－ z）T， 公钥其中β ＝；多项式时间算法EncRand（r，P） 表示在密文扩展过程中生成随机性加密，在函数中输入，输出F ＝其中f1［i］＝b［i］ri ＋pe′1［i］＋。 从而可得到加密形式为RGSW．Enc（μ，p）＝C ＝rP ＋pE ＋μG。 输出扩展密文

其中，Ci ＝［Ci，0，Ci，1］为用户i的RGSW．Enc（）型密文，Xj ＝［Xj，0，Xj，1］＝［BitDecomp（bj － bi）Fi］。

（3） 生成计算密钥：用密文RBGV 与密文RGSW 的混合同态乘法替代两个RBGV 型密文相乘可以降低计算过程中产生的噪声，此外用户密钥的系数限制在｛－1，0，1｝之间，从而密钥交换规程中便不再需要比特分解和模交换技术。

定 义 函 数则从 而 可 得 计 算 密 钥evks ＝｛κm，ξ｝。 其中定义RGSW 的密文C2与RBGV 的密文c1的 混 合 同 态 乘 为BitDecomp（c1）C2。

原BGV 方案中ems是由多项式环上的GSW 加密方案来对参与计算的用户的私钥进行加密的，而在本 方 案 中

解密部分的优化：

提出了一个定向解密协议，增强了数据拥有者对自己明文的控制能力，通过在参与同态计算的用户的中间解密结果中添加对“0”的加密来实现。 以用户i要得到解密结果为例说明定向解密协议的执行步骤。 首先，各自解密自己所对应的密文（类似于门限解密）；之后各参与方用用户i的公钥对“0”加密得到密文ci，各参与方计算ci的和以及上一步中各自的部分解密密文得，并发送给用户i；最后用户i对求和并解密C（μ1，…，μk）modqlmodp。

随后车小亮等［25］也对于以上两种问题提出了优化方法，将低位比特丢弃技术（利用比特分解进行多项式乘法运算时，丢弃一定量的低位比特信息不做处理，不影响最终运算结果的正确性，函数DBitDecomp（bj）＝Dk（BitDecomp（bj）） 表示把向量bj的1 →k位舍弃）应用于计算密钥的密文扩展，从而得到一个优化的计算密钥生成算法，进而提高方案的运算效率。 定义优化后的算法为LDA 算法，原算法为BGV 算法则，用LDA 和BGV 的混合同态乘法运算可得到优化的计算密钥，过程如下。

（1） 定义函数Ψl，i［t］ 和函数φl，i［t′］：当t ＝0时，Ψl，i［t］＝BGV．Enc（pl－1，i，1）， 否 则Ψl，i［t］＝当t′ ＝0 时，φl，i［t′］＝LDA．Enc（pl－1，i，1），否则φl，i［t′］＝LDA．Enc（pl－1，i，其中pl－1，i为辅助公钥集、为扩展私钥；LDA．Enc（pl，i，zl，i）：输入私钥多项式zl，i和公钥pl，i ＝（bl，i，al，i）， 输 出 密 文（rl，ibl，i ＋pel，i ＋zl，i，rl，ial，i ＋pe′ l，i）。

（2） 对函数Ψl，i［t］ 和φl，i［t′］ 进行密文扩展，LDA．Extands－1（φl，i［t′］，k）。 其 中k为 用 户 集。LDA．Extand（ci，0，K）： 输 入ci，0（zl，i）、 辅 助 密 文dl，i（zl，i） 和用户公钥集，则对于任意非用户i可进行计算以下3 步，首先计算DBitDecomp（bl，j） ·di，0， 再 计 算μ。

（3） 获 得 计 算 密 钥evk，evk ＝｛km ＝

优化的结果相比原加密方案的公钥尺寸和计算密钥密文量都相对减少，计算密钥的生成效率有所提高。

2．3 基于近似特征向量的多密钥全同态加密方案

第二代全同态加密使用的密钥交换技术是每次在进行同态乘法之前用一个高维矩阵乘以密文，因此需要存储大量的高维矩阵，从而使存储开销增大。第三代全同态加密以GSW 方案［6］为代表，该类型的加密方案将密文加密为矩阵的形式，使得数据的运算全部为简单的矩阵运算，因此不会出现维数膨胀问题。 虽然该种类型的方案在构造的过程中同样也引入了噪声，但不需要密钥交换技术或模交换技术就可以实现全同态，只需要选择合适的参数就能控制噪声，使其达到正确解密的条件。 此阶段出现的加密方案有CM（15）［8］、MW（16）［9］等。 正是此类方案计算简便、结构简单，使得基于近似特征向量的多密钥全同态加密方案［26］被广泛研究，其构造过程如下。

（1） 初始化GSW．SetUp（1λ，1L）：定义安全参数λ、模数q ＝q（λ）、参数n ＝n（λ）、m ＝O（nlogq）∈Z以及错误分布χ ＝χ（λ），其中χ的边界为B，令l ＝「logq⏋、N ＝nl。

（2） 密钥生成GSW．KeyGen（）： 生成公钥和私钥。

（3） 加密GSW．Enc（pk，μ）： 生成密文形式为其中A为公钥矩阵，R为在加密过程中均匀选取的一个随机矩阵，G ＝In⊗gT为工具 矩 阵，In为 单 位 矩 阵，gT＝（1，21，22，…，2l－1）。

（4） 密文扩展GSW．Extand（）： 此种类型的MKFHE 方案在进行同态运算之前要先进行密文扩展，否则无法参与同态运算。

（5） 同态运算GSW．Eval（C1，C2）： 同态加法运算算法为密文矩阵直接相加，即C1＋C2，同态乘法运算需要引入原像函数G，即C1G－1（C2）。

（6） 解密GSW．Dec（sk，C）： 私钥与密文做内积，结果为近似特征向量的形式，即sC ＝eR ＋μsG，其中s为解密密钥，e←χm。

当前对基于近似特征向量构造的MKFHE 的优化主要是对方案计算效率、密钥生成等的优化。2017 年Li 等［27］提出了一种新的密文扩展技术——改进的线性组合程序（iLCP），用于提高方案的运算效率，除了密文扩展算法同GSW 型方案不同外，其他多项式算法均相同。 密文扩展算法的具体构造流程如下。

（2） 定义矩阵函数Ca，b， 当a ＝b时，Ca，b ＝C＃（C＃为对明文处理之前明文的密文）；当a ＝i≠j且b ＝j时，Ca，b ＝X（j）；否则，Ca，b ＝0。 从而扩展密文即为Ca，b的一系列子矩阵。

2020 年，唐春明等［28］又对此类型加密方案公钥生成不具有独立性问题进行了优化。 MW（16）［9］方案中的密文扩展是在CRS 模型下完成的，每个参与方都共享一个随机矩阵B来生成公钥，因此用户与用户之间的独立性不存在。 对此Kim 等［29］提出了KLP（18）方案，尽管本方案的密文扩展操作不需要CRS，但扩展方法操作复杂，致使方案的计算效率较低。 唐春明等［28］便结合以上两种方案的优势并用工具矩阵对随机对角阵进行编码构造了一个高效的MKFHE。 其具体的构造过程如下。

（1） 初始化函数SetUp（）：与上面相同，只是不生成公共随机矩阵B。

（2） 密钥生成函数KeyGen（）： 私钥的生成方式与上面相同，公钥也与前面类似，只不过是原方案从初始化函数中选择B， 而本方案要在这一函数中从中选取矩阵B。

（3） 加密函数Enc（pk，μ）：与原方案相同。

（4） 密文扩展函数Extand（）：此函数共分4 个阶段进行。 首先用工具矩阵对随机对角矩阵R进行编码得；然后用得到的编码生成扩展密文所需的辅助信息之后用私钥tj和辅助信息X做内积的形式对辅助信息 进 行 解 码 操 作， 得AiR）＝tjAiR ＋ej（modq），最后定义扩展密文

3 展望

本文对多密钥全同态加密的发展及其优化过程进行了梳理和分析。 不同学者针对各类型最初的MKFHE 的局限性提出了不同的优化方案［30－32］，李宁波等［31］主要侧重于原始加密体制的构建；文献［32］主要侧重推动多密钥全同态加密发展的自举技术。 原始方案的进一步优化使得优化后的方案具有更高的运算效率、存储开销普遍降低以及加密过程更加简便等优势，对MKFHE 的发展也起着至关重要的作用，文献［33］应用优化后的MKFHE 方案提高电力物联网数据的安全性。 目前优化后的方案仍面临一些问题和挑战：

（1） 提高多密钥加密方案的安全性。 目前构造的大部分方案的安全性均只满足选择密文攻击的不可区分性安全，部分高效的多密钥加密方案只能够抵抗被动敌手攻击的选择明文不可区分性安全。 目前还不存在满足自适应选择密文攻击的不可区分性安全的加密方案。 因此，高效的自适应选择密文攻击的不可区分性安全的多密钥加密方案将会对密码学的发展具有重大意义。 另外，云环境下用户之间的数据“交易”越来越密切，多用户数据之间的安全性分析也成为了信息安全领域重点关注的问题。

（2） 提高方案的综合效率。 综合效率仍是制约多密钥全同态加密发展的一个因素。 将单密钥密文扩张成多密钥密文时扩展操作过于复杂，且扩展后的密文体积也随着参与方的数量随之增大，给计算存储都带来了挑战。 此外只能执行单比特运算，效率偏低。 这些都限制了多密钥全同态加密的实用价值。 下一步，需要在尽可能扩展多密钥全同态加密功能性的基础上，针对如何减小方案中密文的尺寸，尽可能地减少方案的密文量、密钥量以及计算复杂度，进一步提高同态运算效率和存储效率等继续展开研究，将传统的单密钥的成熟的优化技术应用到多密钥之中，从而进一步促进多密钥全同态加密的实用化进程。

（3） 探索多密钥全同态加密在安全多方计算中的应用。 由于格具有天然的抗量子攻击的优势，因而在后量子时代成为安全多方计算协议的设计思路之一。 同时作为安全多方计算重要分支的私有信息检索（PIR），未来具有非常高的研究前景。 将基于格的多密钥加密方案应用于安全多方计算可有效抵御外界的攻击，也是当前密码学研究热点问题之一。如何设计行之有效的全同态密码学算法获得通行轮次更低计算开销更小的安全多方计算协议仍是一个公开问题。

（4） 构建MKFHE 在标准模型下的研究方案。随机语言模型下，MKFHE 方案中涉及到的哈希函数是安全的一个隐患。 满二秩差分编码函数FRD和最新的基于格的可编程哈希函数PHF 的研究成果可为MKFHE 在标准模型下的研究提供良好的帮助。

（5） 提供MKFHE 中多用户身份的验证，将加密方案和签名方案相结合，构建多密钥全同态加密签名一体化方案。 加密签名一体化方案能够公用系统参数，简化方案步骤，进一步提高方案效率。 目前基于格的签密方案研究非常少，也是未来研究的全新挑战。

总之，目前信息安全日益受到更多关注，无论密码学前沿的MKFHE，还是其他安全方案，都迫切需要将理论在实际应用中平稳落地。