微小型金属壳谐振陀螺静电激励电路设计
2023-09-23王靖骁赵文江
韦 任,刘 宁,苏 中,王靖骁,赵文江
(北京信息科技大学高动态导航技术北京市重点实验室,北京 100192)
0 引言
微小型金属壳谐振陀螺(以下简称:金属谐振陀螺)是一种哥氏振动陀螺,因其敏感结构谐振子采用合金制成,不仅具有传统谐振陀螺的惯性品质,而且具有结构强度高、抗高过载、环境适应能力强和动态范围宽等特点,在极端条件下是重要的角速率测量传感器[1-5]。金属谐振陀螺与其他振动陀螺相比,由于金属材质的原因需要高频高压的激励源,因此金属谐振子的激励电路设计成为重点研究方向[6]。
王鑫等提出一种基于两对电极产生静电力的激励方法,得出结论:当直流偏置量和交流信号振幅相等时激励产生的振幅最大[7];周冠卿等研究了基于PZT压电陶瓷压电效应驱动谐振子的方法[8];樊尚春等提出基于频域分离法的单端口静电激励—电容检测方式,利用同一个电极实现对谐振子振动的激励和检测[9];王剑秋研究了一种基于电磁铁的电磁激励谐振子的方法[10]。目前对谐振子的常见激励方式有静电激励、电磁激励和压电激励等[11],其中静电激励属于非接触式激励,因此广泛应用于各种谐振陀螺[12]。
本文提出了一种静电激励电路,采用推挽式升压电路产生正负高压。通过直流逆变电路实现高压直流逆变为高频高压输出,电压幅值可达500 V,频率为200 kHz,对金属谐振子施加足够的静电力驱动振子谐振,维持主振型的驻波振荡。通过搭建高压和直流逆变电路仿真模型,最终确定了电路的最佳性能参数,绘制电路板测试实际电路效果,验证设计的可行性。
1 金属谐振陀螺原理
1.1 金属谐振陀螺敏感器件
金属谐振陀螺敏感器件由金属谐振子和电极基板组成,如图1所示。谐振子选用高强度合金材料制成,平面电极采用稳定的石英材料加工成型,并对表面进行金属化精密处理。在电极基板上等角度分布16个电极片,金属谐振子上有48个唇沿对应各个角度电极片。振子和电极基板通过内部支撑杆完成装配,调节支撑杆高度可精确控制唇沿和电极间距,保证唇沿与平面电极具有微小间隙,形成平面电容对金属谐振子施加静电力进行驱动和检测。

图1 金属谐振陀螺敏感器件结构图
1.2 全角模式
全角模式通过幅度调制把角速率调制到2个振动模态的位移,然后进行幅度解调得到进动角,如图2所示[13]。a为主振型振幅,b为外界角速率Ω产生的从振型振幅,ω为谐振频率,因此进动角α为

(1)
式中k为比例系数。
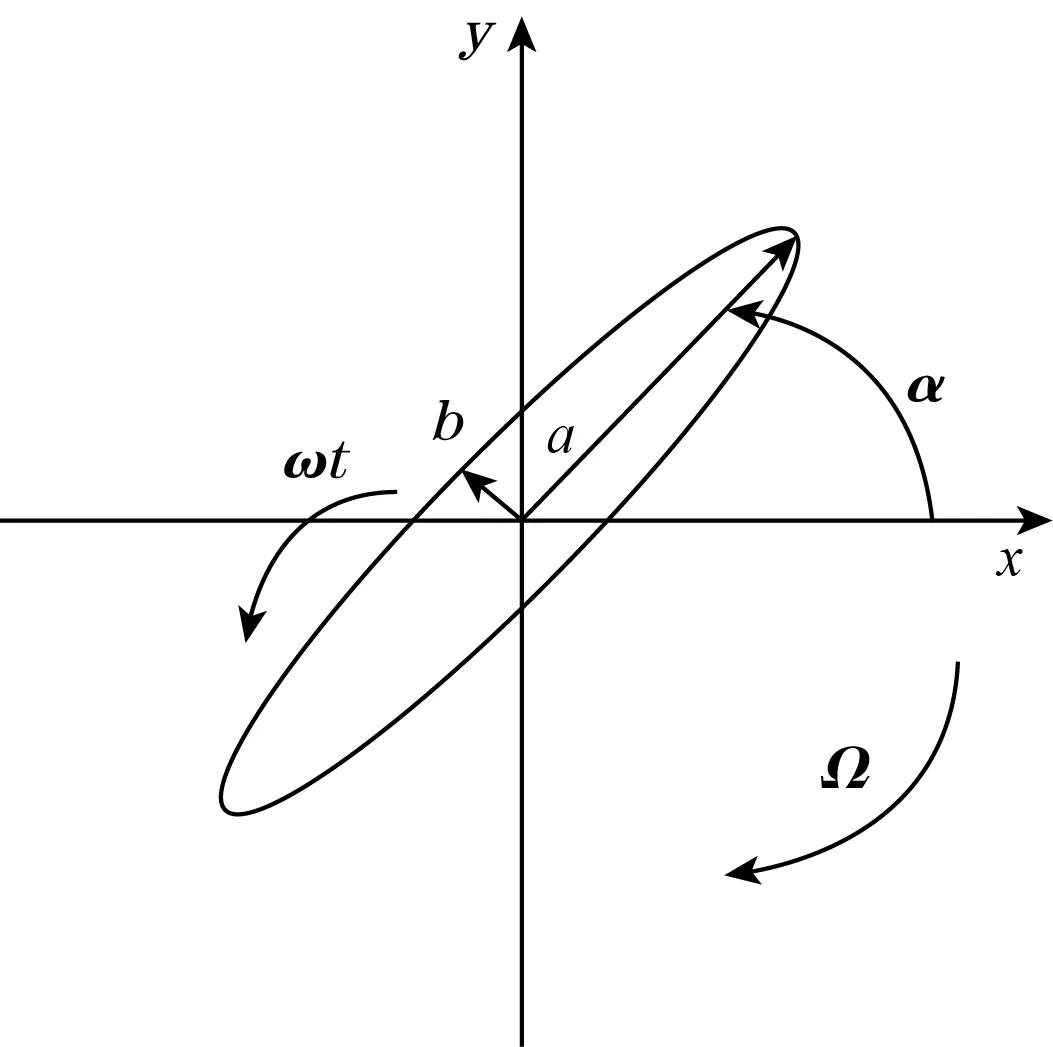
图2 转动谐振图
由式(1)可知,进动角与旋转角度成线性关系,进动角度可以通过解调x(t)、y(t)实现,因此全角模式可直接得出旋转角度,具有较大的测量范围。
1.3 静电力模型
实际工作中存在阻尼损耗,上述全角模式需要主振型维持恒定驻波。金属谐振子唇沿和平面电极可视为一对平行电极板,如图3所示。通过激励电路施加电压,电压产生静电力维持主振型的驻波振荡。

图3 静电力驱动
图3中d为极板目前距离,S为极板相对应面积,x为极板初始距离,Δx为谐振子唇沿的形变量。平行极板之间电荷能量E为
(2)
式中:C为平行板间电容;U为平面电极驱动电压。
静电力F可表式为
(3)
式中静电力为方向向下的吸引力,因此为负。

(4)
式中:Ud为直流电压幅值;Ua为交流电压幅值;ωa为交流电压频率。
由式(4)可知,静电力和驱动电压的平方成正比,因此施加高压可提供充足的静电力激励金属谐振子,保持主振型恒定驻波。
2 静电激励电路设计
静电激励电路的设计需要考虑诸多问题,例如输出频率、静电激励的幅值、器件的选型以及陀螺的灵敏度,谐振陀螺灵敏度Sy公式为
(5)
式中:A为激励幅值;Q1和Q2分别为驱动和检测品质因数;ωd为驱动角频率;ωy为驱动模态固有角频率;m为谐振子质量[14]。
由式(4)可知,通过控制激励电压可控制静电力大小。由式(5)可知,激励幅值A与金属谐振子的灵敏度Sy成正比,因此高压可提高谐振陀螺灵敏度。
研究表明:当激励电压幅值为500 V,频率为200 kHz能够满足金属壳谐振子激励需求。针对产生高频高压的要求,本文采用升压电路将输入电压转化为正负高压,驱动电路将控制信号转化为驱动信号,然后将二者输入逆变电路产生高频高压,整体电路框架如图4所示。
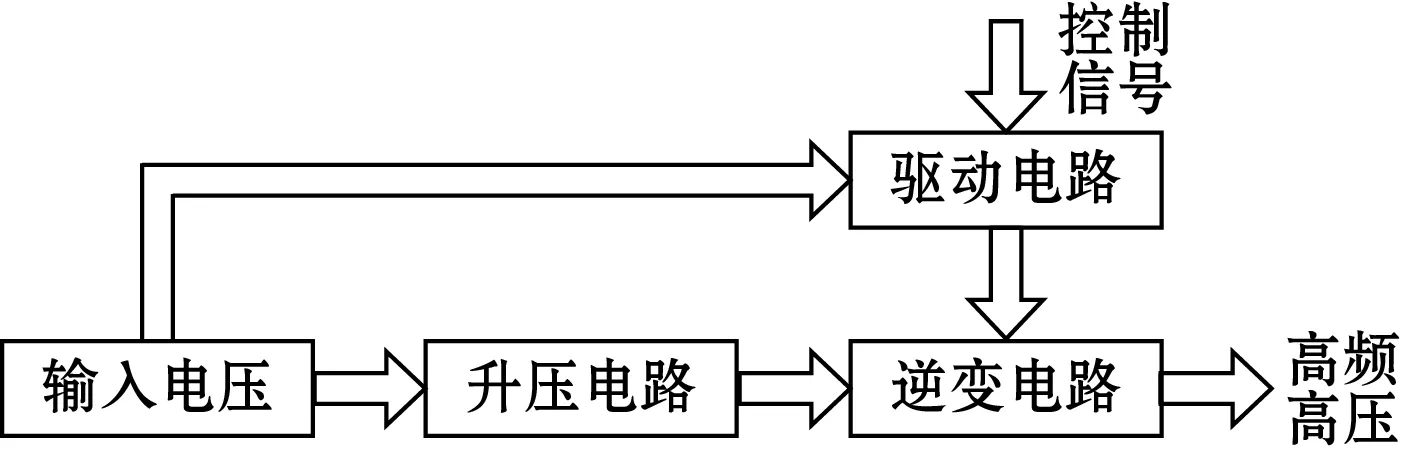
图4 整体电路框架图
2.1 升压电路设计
在电路中为了产生正负高压,通常采用变压器结构,一方面可实现多路输出,调整匝数实现低压-高压的转化,另一方面隔离输入输出回路,提高系统安全性。变压器结构中推挽式变压器效率高、瞬态性能好并且结构简单,只需直流稳压源和驱动2个开关管,变压后可实现双路输出,满足设计需求,如图5所示。

图5 推挽式升压电路结构图
选用DC-DC电源芯片WRF1224S稳定输出24 V电压,提供芯片输入电压和变压器中间抽头电压。变压器设计为推挽式升压电路,因此采用高压PWM控制器芯片LM5030。芯片输出引脚OUT1和OUT分别产生占空比小于50%的PWM波,输出频率可由外接电阻调节,驱动NMOS管N1和N2交替导通在变压器一次侧施加交变方波电压。
由于推挽式电路结构,当一个开关管导通时另一个需承受2倍的输入电压,本文输入电压为24 V因此选用耐压大于48 V的开关管。最后变压器二次侧升压后经过二极管D1和D2半波整流,C1、C2、R1和R2构成阻容滤波平稳电压和滤除毛刺,同时分成U+和U-两路高压输出,提供直流逆变电路使用。与此同时,为保障输出持续稳定,设计变压器反馈线圈产生反馈电压,电压经过反馈电路处理后输入到控制器芯片的反馈引脚,经过内部误差放大后与PWM比较器比较,优化输出引脚占空比,保证输出电压稳定实现闭环调节。
2.2 直流逆变电路设计
为了将直流高压转化为正弦高压,通常采用逆变电路,首先控制信号经过隔离后输入到驱动电路,然后输出的驱动信号控制逆变器交替通断,使得高压交替输出方波,最后方波经过滤波电路最终实现输出高压正弦波形,电路设计如图6所示。
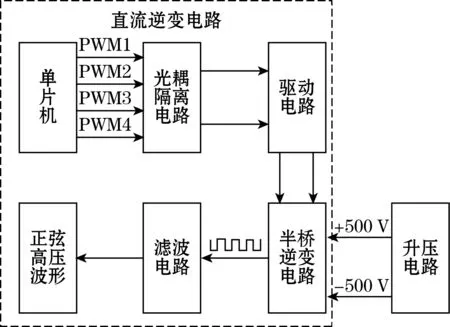
图6 直流逆变电路设计图
控制信号采用单片机输出的4路PWM波,因电路后端驱动高压输出,为防止高压烧毁单片机设计光耦合隔离电路。通过四通道光耦合隔离器,实现每个通道互不影响的同时,实现“电—光—电”之间的转化,使输出端信号对输入端信号不产生影响,因此信号抗干扰能力强,工作稳定性高并且保护单片机。由于光耦合隔离器具有延迟时间,为实现高频输出,设计输入信号PWM1和PMW2互为反相的PWM波,信号经过隔离器后再经过三极管合并为一列交替信号,输出到后端栅极驱动器,PWM3和PMW4同理产生与之反相的信号。
经过光耦合隔离后的信号电流较低,不能驱动后端NMOS管,因此设计驱动模块。设计考虑驱动电压为±500 V,选用最高可耐受600 V高压的栅极驱动器UCC27714D。通过芯片HI和LI引脚输入电平和频率控制HO和LO引脚的输出,驱动后端NMOS管的通断,输出逻辑见表1。

表1 输出逻辑表
针对高压和高频的要求选用IPD70R360P7S,耐压700 V并且开关延时时间在ns级别的NMOS管。HO和LO交替输出使NMOS管交替导通实现DC-AC逆变,如图7所示。因NMOS管DG、GS之间存在结电容,所以并联R3、R4和C3组成阻容电路,释放结电容存储的电荷防止NMOS管损坏。通过并联快速恢复型二极管D2可加快NMOS管开关速度,有益于高频输出。半波整流输出的交变方波由傅里叶展开式(6)可知,其中n为奇数,经过滤波电流滤除高次谐波,可输出高压正弦波。
(6)
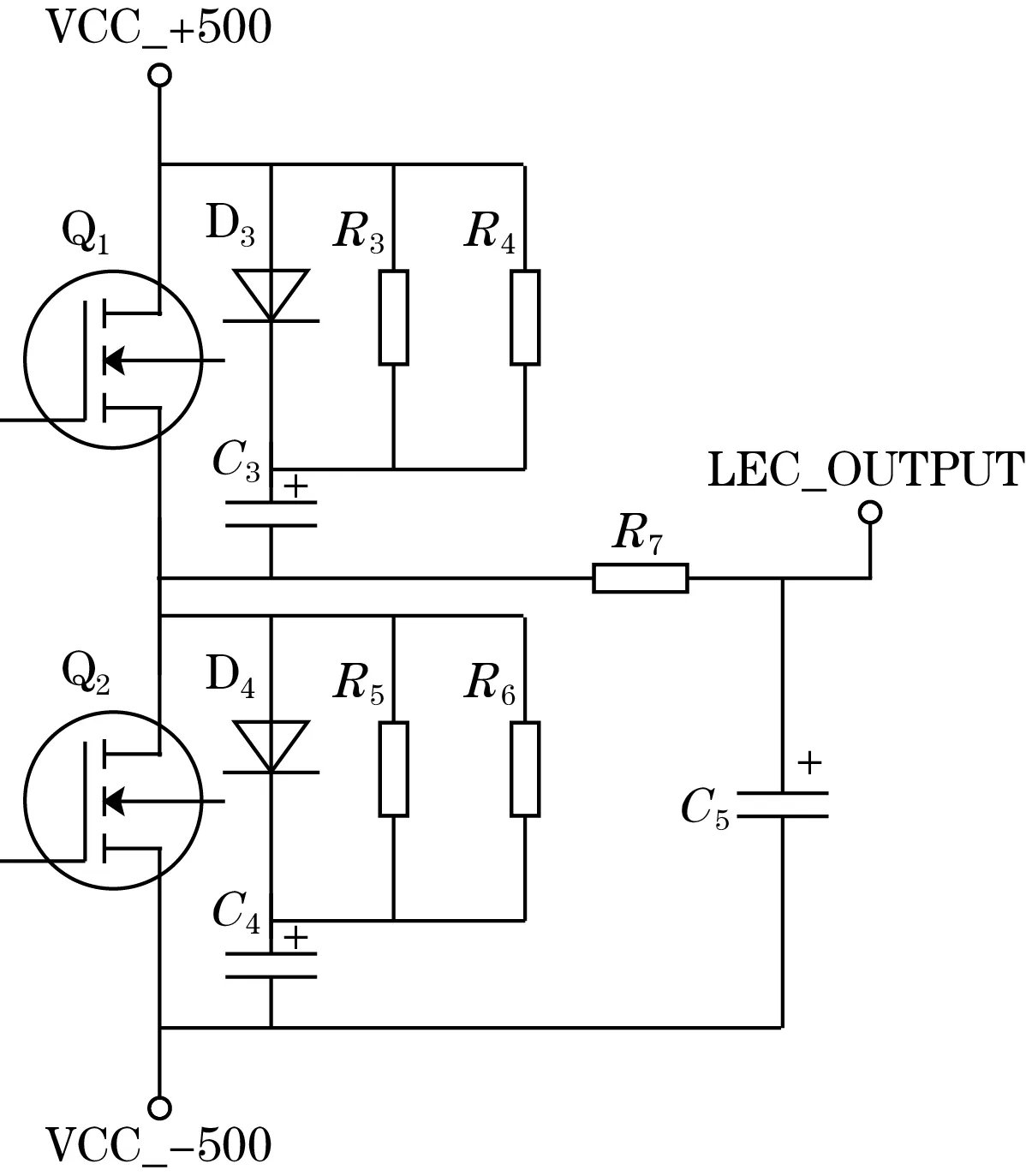
图7 半波整流滤波电路
3 仿真和检测结果
3.1 升压电路仿真
为了验证升压电路设计可行性,使用EDA软件建立仿真模型,模型中使用24 V恒压源代替DC-DC芯片输出,简化模型结构。LM5030输出频率设置为70 kHz,变压器变比为1∶21.7,输出正负高压如图8所示。推挽式升压电路可以同时输出正负两路高压,电路0~1 ms启动阶段无电压产生;1~5 ms处于RC滤波过程电压缓慢上升后回归平稳;5 ms后电路输出趋于稳定。仿真输出达到±500 V,可充分激励谐振子提高灵敏度,符合设计目标。具体稳定输出后纹波电压如图9所示。

图8 正负电压输出

图9 输出电压纹波
由图9可知,稳定输出后电压围绕500 V振荡,产生纹波电压为2.96 V,占输出电压的0.59%,说明输出电压平稳,符合电路要求。
3.2 直流逆变电路仿真
为了验证直流逆变电路设计和物料选型的可行性和准确性,选择理想电路器件建立仿真模型,使用恒压源输出±500 V电压,设置驱动信号的周期为5 μs、脉冲值为3.3 V、脉冲时间分别为0.8 μs和0.5 μs,开关管交替导通后产生交变方波高压,如图10所示。

图10 交变方波高压
由图10可知,方波的幅值为500 V,频率为200 kHz以及周期5 μs与驱动信号周期一致,说明符合电路设计预期,可实现PWM信号控制高频输出。模型在仿真5 μs后开始稳定输出方波,在电压为0 V附近易出现失真,是由于上下开关管交替导通时开启延时和关闭延时造成的问题,对后面低通滤波的结果也会产生一定影响,针对该问题可提高开关管开闭速度进行改善,后续需要进一步优化。
方波高压通过低通滤波转变为正弦波,本文通过改变电阻值改变截止频率,比较200、300、350、400 kHz不同低通截止频率的滤波效果并与幅值500 V、频率为200 kHz正弦波进行对比,因滤波过程中会使得电压幅值降低,所以200 kHz和300 kHz需要提高输入电压保证滤波后输出达到500 V,仿真对比结果见图11。由图11中4种滤波效果对比可知,在-300~300 V时与标准正弦波偏差较小,位于两端电压时偏差较大。为更加量化地对比上述波形图与幅值500 V正弦波的偏差,计算每个时间点对应2条曲线值的差值,然后计算所有差值平均值占电压有效值的百分比,不同频率对应参数和差值百分比结果如表2所示。
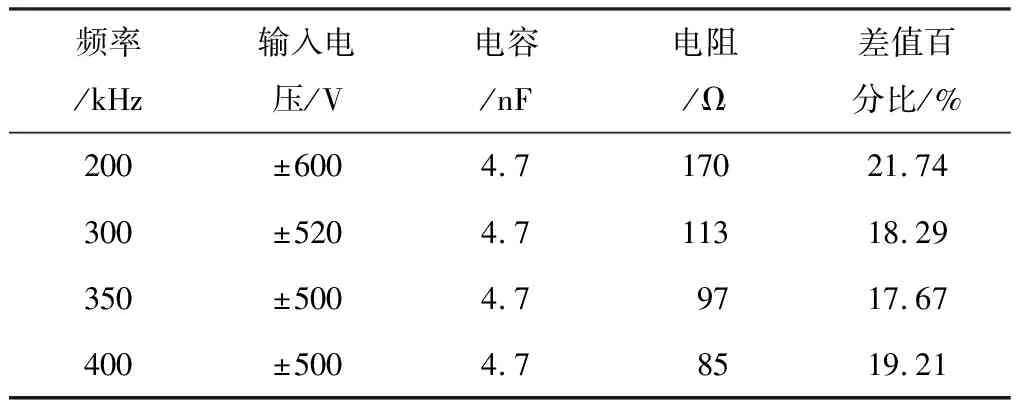
表2 不同截止频率参数对比表
由表2可知,随着截止频率的上升,差值百分比出现先降低后升高的现象。原因是截止频率过低导致幅值衰减,输入电压增加的同时有效信号也被过度衰减,频率过高则不能滤除高次谐波。因此为得到输出频率为200 kHz、幅值为500 V的输出电压,最佳截止频率为350 kHz,差值百分比为17.67%,符合预期设计目标。

(a)200 kHz滤波后波形图
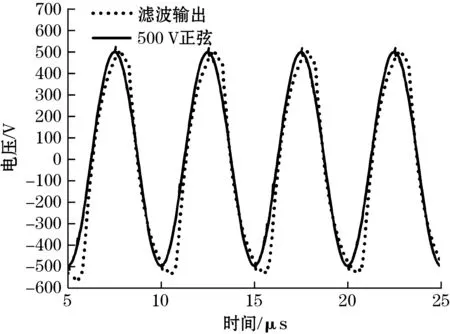
(b)300 kHz滤波后波形图

(c)350 kHz滤波后波形图

(d)400 kHz滤波后波形图
3.3 电路测试
根据金属谐振陀螺敏感器件,制造样品如图12(a)所示。根据上述仿真结果说明各部分电路设计方案可行,高压电路采用推挽式升压电路,直流逆变采用信号源控制半波逆变电路。绘制电路板并装焊器件如图12(b)所示。通过示波器、稳压电源、金属谐振子、测试电路板和信号发生器构建测试系统,如图13所示。

(a)金属谐振陀螺敏感器件

(b)测试电路板
稳压源提供5 V输入电压,信号发生器模拟单片机输入200 kHz方波,观察示波器输出波形。测试结果与仿真一致可实现200 kHz的高频正弦输出。

图13 整体测试系统
4 结束语
本文提出了一种金属谐振陀螺的静电激励电路,利用直流逆变电路对正负高压进行逆变得到高频高压正弦输出,施加到平面电极激励金属谐振子。通过仿真证明升压和直流逆变电路设计的可行性,经过对比不同截止频率的输出结果得出:为了得到频率为200 kHz、幅值为500 V的高压高频输出,最佳截止频率为350 kHz,输出差值百分比为17.67%。最后通过建立测试系统观测电路板输出结果,进一步说明方案的实用性。
