变张力细长柔性立管涡激振动响应特性数值研究

高 云，潘港辉，刘 磊，柴盛林

（1.哈尔滨工业大学（威海）海洋工程学院，山东 威海 264209；2.安徽长江液化天然气有限责任公司，安徽 芜湖 241000；3.西南石油大学油气藏地质与开发工程国家重点实验室，成都 610500）

0 引 言

立管是连接海上浮式平台与海底井口的装置，在深海油气工程中应用广泛。当漩涡流经立管时，在一定的雷诺数范围内会导致立管发生振动，这种现象被称为涡激振动（VIV）[1]。涡激振动是一种非常典型的流固耦合问题[2]。一般认为，VIV 引起的动载荷会导致立管产生疲劳损伤甚至疲劳破坏[3-5]。由于立管处在水下，其维护费用很高，立管若发生疲劳失效，会造成巨大的经济损失。因此，可靠地预测立管涡激振动响应是其结构设计过程中的关键问题之一。在过去的几十年里，许多研究者对VIV问题进行了研究。由于立管VIV 振动具有非常复杂的流固耦合特性，早期的研究大多集中在刚性圆柱上。对刚性圆柱体的研究可以揭示振动问题的许多基本机理，如锁定现象和滞回特性等[6-9]。

近年来，随着深水油气勘探的迅速发展，许多学者对大长径比柔性结构的VIV响应特性展开了研究。根据研究方法，这些研究主要可分为物理实验和数值模拟[10-16]。实验方法虽然能得到丰富可靠的结果，但也存在一定的局限性，如模型规模有限、成本昂贵、复杂流剖面生成困难等。与实验方法相比，数值方法可以克服其中的一些局限性，例如可以显著降低研究成本，更容易实现复杂流剖面。数值计算方法基于流体力的确定方法可分为两种。一种方法是计算流体动力学方法（CFD），它通过直接求解Navier-Stokes 方程来计算流体力；另一种方法是半经验方法，它是根据经验系数来确定流体力。与CFD方法相比，半经验方法的显著优点是计算量小。因此，为了满足对细长柔性结构的VIV响应特性进行复杂多参数敏感性分析的要求，有必要提出一种能快速预报柔性结构VIV 响应特性的数值模型。近些年来，尾流振子法被广泛应用于预测细长柔性结构的VIV响应特性，如表1所示[17-28]。

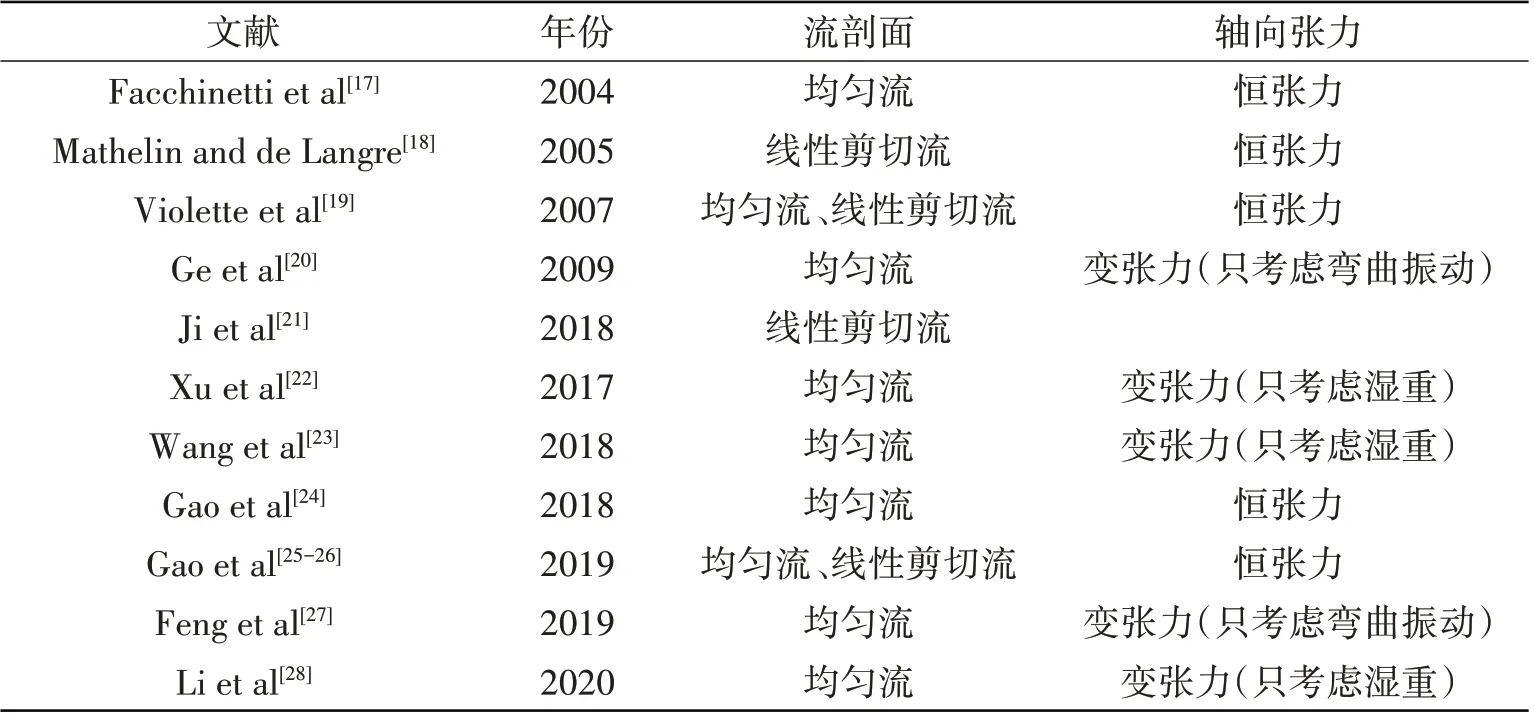
表1 部分基于尾流振子模型的柔性圆柱体VIV响应研究Tab.1 Selected VIV studies of a flexible cylinder using a wake oscillator model

由表1 中最后两栏可以看出：针对柔性立管的研究，根据考虑轴向张力的特征，可分为恒张力研究和变张力研究。在变张力研究中，目前考虑的张力成分均比较单一：其中一部分研究只考虑了湿重，而另一部分研究则只考虑了弯曲振动。而在实际深海工程中，柔性立管轴向张力同时包括由湿重引起的等效张力和因结构弯曲振动而带来的额外张力。此外，在实际深海工程中，真实海流既不是均匀流，也不是线性剪切流，而是阶梯流[29-30]，这种海流的流剖面更接近指数剪切流。综上，准确预报出真实海洋环境中变张力柔性立管的涡激振动响应特性，对海洋立管早期的合理设计和服役期间的安全工作均具有重要的理论和工程价值。

本文从实际海洋工程环境出发，建立变张力柔性立管涡激振动响应模型。考虑立管湿重和弯曲振动的作用计算轴向张力，采用二阶中心差分法编程计算柔性立管的涡激振动响应。基于数值计算结果，系统地比较线性剪切、指数剪切以及真实阶梯流剖面下柔性立管的VIV 响应特性，并进一步阐述三种流剖面作用下柔性立管涡激振动响应特性的特有规律。

1 模型描述

如图1 所示，考虑一初始长度为L、外径为D、内径为d的细长柔性立管在来流作用下引起的横流方向涡激振动响应问题。立管两端采用铰接边界条件，取坐标原点O为立管的下端，X方向为顺流方向，Z方向为铅直方向，Y方向则是横向振动方向，X、Y和Z三个方向形成右手直角坐标系。柔性立管上受到的张力为Θ（Z，T），柔性立管的弯曲刚度为EI，其中E和I分别是弹性模量和横截面惯性矩。

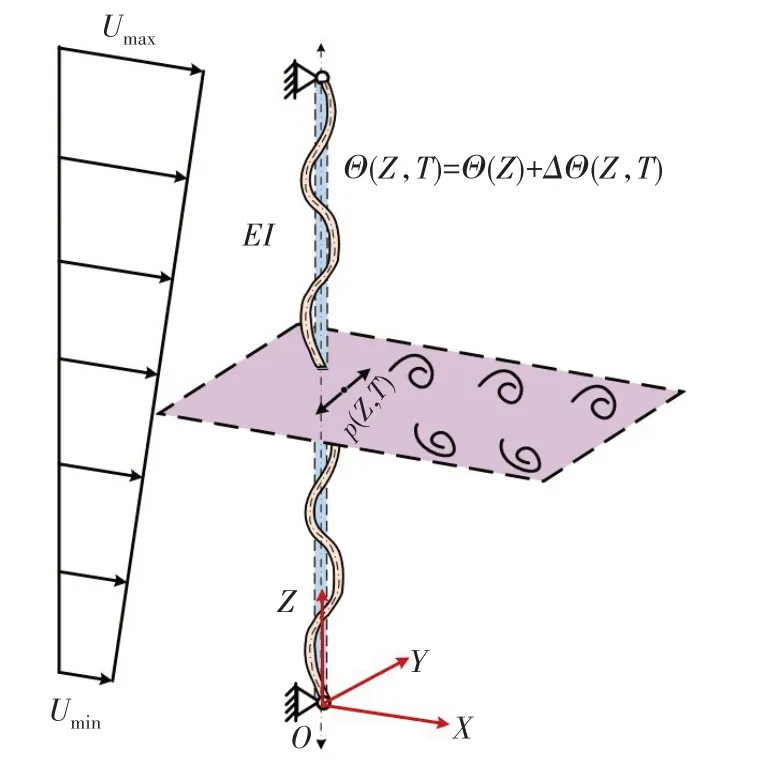
图1 线性剪切流作用下时变张力柔性立管模型Fig.1 Flexible riser with time-dependent varying tension subjected to a linear shear flow

本文中分别计算了三种不同类型的流剖面：线性剪切流、指数剪切流和真实阶梯流剖面。这里为了研究方便，流剖面中最小流速取为最大流速的0.05 倍（即：Umin=0.05Umax）。其中线性剪切流剖面和指数剪切流剖面的计算公式可表示为

式中，U（Z）表示位于Z处流剖面的流速。对于真实阶梯流剖面，通过最大流速乘以归一化流剖面系数得到，该系数来自于Gao等[30]使用的值，如表2所示。将实际阶梯流剖面沿立管轴线分为10个截面，每个截面的流速值呈线性变化特性，Nf为每段截面端点处的归一化系数。由表2 可以看出，对于本文研究的阶梯流，Umin=0.05Umax，这与前面介绍的线性剪切流和指数剪切流中最小流速与最大流速的关系相同。

表2 真实阶梯流剖面归一化系数Tab.2 Normalized coefficients for a real stepped flow

将图1 中的柔性立管看作是细长张力梁模型，建立如下振动方程：

式中：rs和rf分别表示结构阻尼系数以及流体阻尼系数；mtotal为单位长度的振动系统质量，包括柔性立管结构质量、立管内部流体质量和立管外部流体附加质量三部分，可表示为

式中：ρs、ρf和ρw分别为柔性立管材料密度、立管内部流体密度和立管外部流体密度；CM为附加质量系数，对于圆柱体，CM=1.0。这里假设结构阻尼系数rs为0，流体阻尼系数可表示为rf=γΩfρD2，其中：Ωf为根据斯脱哈尔关系式计算得到的局部漩涡脱落频率，Ωf=2πStU（Z）/D，St为斯脱哈尔数；γ为粘滞力系数，γ=--CD/4πSt，--CD为平均拖曳力系数，这里取为1.2。式（2）中，p（Z，T）为单位长度立管受到的升力，可表示为

式中，CL（Z，T）为升力系数，CL（Z，T）=CL0·q（Z，T）/2（CL0为静止圆柱的升力系数，这里取为0.3；q（Z，T）表示圆柱体Z处在Y方向的尾流振子的运动）。式（2）中的Θ（Z，T）表示轴向张力，若同时考虑湿重带来的张力变化以及结构弯曲振动带来的额外张力变化，其表达式可写为

式中，Θ（Z）表示仅考虑湿重时立管的轴向张力。此处引入顶张力系数K，假设立管上端所受张力为Ttop，那么Ttop可表示为Ttop=K×L×Wr，其中Wr为立管结构的湿重，可表示为

式中，g为重力加速度。由图1 可知，坐标系原点位于结构下端，则任意坐标位置Z处的Θ（Z）可由立管上端张力和单位长度结构湿重表示为

式（5）中，ΔΘ（Z，T）为考虑弯曲变形带来的额外张力，可表示为

式中，Ap为立管横截面积（Ap=（D2-d2）π/4），E为杨氏弹性模量，S为结构发生弯曲变形后的瞬时长度。

在立管轴线上任取一个微元段dZ，若忽略顺流X方向振动，只考虑横流Y方向振动，则变形后的微元长度dS可表示为

针对整个立管，在某一瞬时立管的总长度S可由式（9）进行轴向积分得到，并进一步简化为

联立式（5）、（7）、（8）和（10），可得到同时考虑湿重以及弯曲变形情况下立管的轴向张力为

采用改进的Van der Pol方程来满足尾流振子的非线性特征，表示如下：

式中，A和ε为经验参数，A=12，ε=0.3。将式（2）和式（12）转换为无量纲形式，令：

式中，Ωref为依据参考流速Uref计算得到的斯脱哈尔漩涡发放频率，Ωref=2πStUref/D。将式（13）中三个等式分别代入式（2）和式（12）中，整理得到无量纲形式的结构振动方程以及尾流振子方程：

式中，ωf（z）表示流剖面参数，ωf（z）=Ωf/Ωref=U（z）/Uref。这里将流剖面中的最大流速Umax选作Uref。质量比μ、系统无量纲参数ML、无量纲单位长度湿重a、无量纲弯曲刚度b和无量纲变化张力c（z，t）可分别表示为

2 数值方法

假设柔性立管无量纲总长度L/D可划分为M段，计算无量纲总时间ttotal可划分为N段，那么，计算空间步长为Δz=L/（D×M），计算时间步长Δt=ttotal/N。被离散后的M+1 个空间点可表示为：z=zi（i=0，1，2，…，M）；被离散后的N+1 时间点可表示为：t=tj（j=0，1，2，…，N）。假设tn时刻zm位置处对应的无量纲参数y和q可表示为和，那么式中各偏导数项的二阶精度差分格式可表示为

将式（17）中的差分格式代入式（14）和式（15）可得

式（18）中c（zm，tn）表示如下：

由式（16）可以看出，表达式Θ的第二项ΔΘ（z，t）含有积分项，这里为了简化计算，将式（17）中的差分格式代入积分项，并对其进行累加求和处理，可得Θ（zm，tn）的表达式为

将式（18）～（19）中的迭代表达式形式作进一步简化，转化为显性表达式形式表示如下：

假设y的初始条件（t=t0）位移和速度均为0，即y=∂y/∂t=0；q的初始条件设为一个波数的微幅扰动，且∂q/∂t=0，结合式（17）可得到：

将式（24）依次代入式（22）和式（23）中得到t=t1时刻y和q的值，表示如下：

至此求解得到t=t0以及t=t1时刻y和q的值。在t=t2时刻以后，需要使用到边界条件。边界条件设为两端铰接，即y在z=0时刻和L/D处的位移为0，弯矩为0，可表示为

当m=0和m=M时，需要用到位移为0的边界条件，即

当计算m=1和m=M-1时，需要用到弯矩为0的边界条件，由弯矩为0，联立式（17）可得到

对于式（22），先赋予初始条件式（25）和边界条件式（27），即对于t0时刻zm处的y，t1时刻zm处的y，tn时刻z0处的y，以及tn时刻zM处的y在求解开始前都为已知。当n≥1且0≤m≤M时，通过式（22）循环迭代求解y，需要注意当求解m=1 和m=M-1 这两个位置的y时，需要用到式（28）弯矩为0 的边界条件。当tn+1时刻zm处的y已知，便可依据式（23）求得tn+1时刻zm处的q，依此类推对式（22）和式（23）进行迭代求解。本文的数值方法已经在过去的研究中得到了充分的验证［24-26］。因此，在这里并没有再次对数值模型进行相关验证。

3 结果与讨论

在以往的研究中，我们主要研究了具有恒张力模型的柔性圆柱体VIV响应特性。然而，这里我们着重研究柔性立管在时变轴向张力下的VIV 振动响应特性。因此，这里使用的数值模型中轴向张力部分比以往多考虑了湿重和弯曲振动带来的影响[24-26]。研究过程中使用的主要参数与Xu等（2017）[22]使用的参数值相同，如表3所示。

表3 立管模型参数Tab.3 Parameters of the riser model

3.1 涡激振动位移研究

图2给出了三种不同线性剪切流剖面下细长柔性圆柱体的无量纲振动位移响应。三种线性剪切流剖面的最大流速Umax依次为1.5 m/s、2.0m/s 和2.5 m/s，最小流速均为最大流速的0.05 倍，即Umin=0.05Umax。图2中，第一列给出了三种不同最大流速对应的线性流剖面，第二列给出了结构振动位移响应RMS值，第三列给出了结构振动位移响应最大值，第四列给出了结构振动位移响应包络线。由图中的第二列可看出：当最大流速为1.5 m/s、2.0 m/s 和2.5 m/s 时，结构振动主导模态依次为10 阶、13 阶和16 阶，这说明结构振动主导模态阶数随最大流速的增加呈上升趋势。由结构振动位移RMS 值可看出：在结构两端，节点处与腹点处的位移值差别较大，说明此时结构振动位移响应由驻波占主导；与结构两端区域相比，中间区域附近节点处与腹点处的位移值差别相对较小，这说明此时结构振动位移由行波占主导。由图2中第四列的振动位移包络线同样可看出：所有节点处的振动位移均明显不为零，说明沿整个轴线方向上，结构振动位移响应均呈现出明显的行波特性。

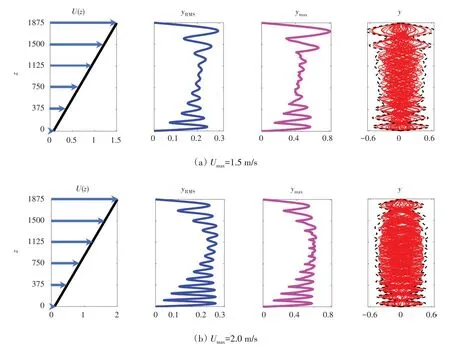
图2 线性剪切流时三种不同最大流速下细长柔性圆柱的均方根、最大位移值以及位移包络线的变化规律Fig.2 RMS,maximum values of the VIV displacements and VIV displacement envelopes of a long flexible cylinder under three different Umax for a linear shear flow

图3给出了三种不同线性剪切流剖面下某个稳态时间段内无量纲振动位移随时间和空间的变化云图。图2 中第二列和第四列中所体现出的结构振动的行波响应特性在图3 的云图中得到了更为明显的体现。云图不仅能反应出结构振动的行波响应特性，更能非常方便地判断出行波的传播方向和传播速度。如图中白色箭头所示，行波的传播方向均为从流速较大的上端区域传播到流速较小的下端区域。通过对比三种不同流速下的位移变化云图可看出：在选取的某稳定无量纲时间段（无量纲时间段为20）内，随着最大流速的增加，结构行波在结构轴线位置上传播的距离逐渐减小，这说明随着最大流速的增加，结构振动响应的行波传播速度呈下降趋势。

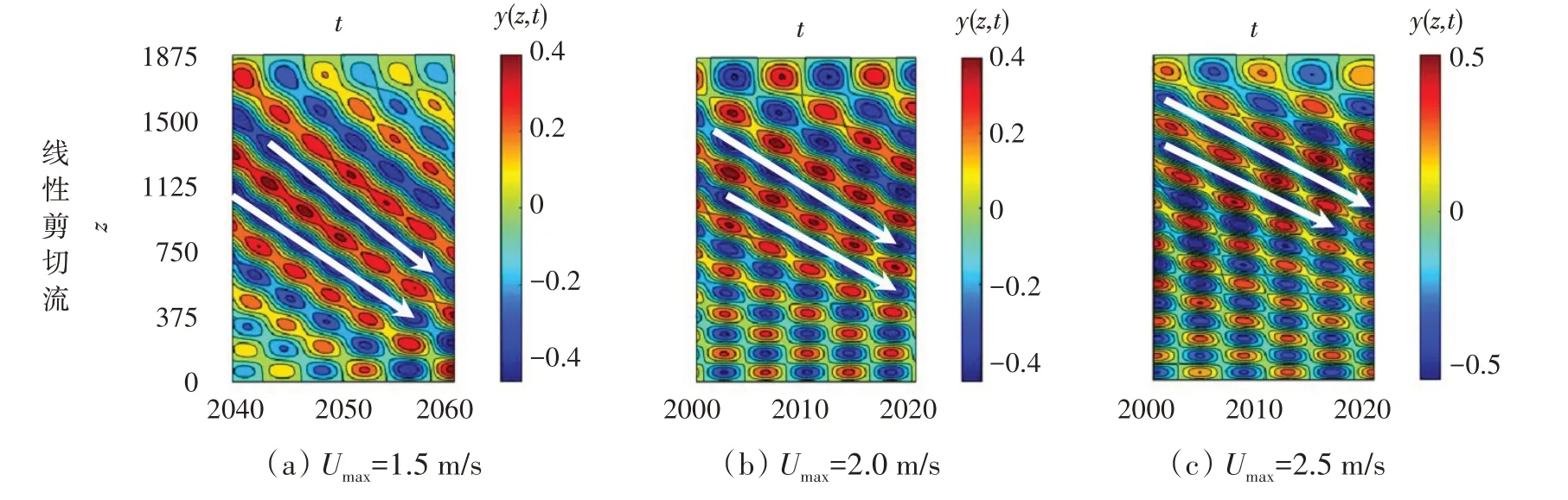
图3 线性剪切流时三种不同最大流速下细长柔性圆柱的位移随时间（t）和位置（z）的变化规律Fig.3 Displacement evolutions versus time and span location of a long flexible cylinder under three different Umax for a linear shear flow

图4给出了三种不同指数剪切流剖面下细长柔性圆柱体的无量纲振动位移响应，图5给出了三种不同指数剪切流剖面下某个稳态时间段内无量纲振动位移随时间和空间的变化云图。由图4（a）的第二列、第四列和图5看出：当最大流速为1.5 m/s时，在结构上端点附近，振动位移响应由驻波和行波共同主导；而在结构的中部以及下部区域，振动位移响应完全由驻波占主导，但同时具备轻微的行波特性。由图4（b）和图4（c）可看出：随着流速的增加，当最大流速为2.0 m/s和2.5 m/s时，结构振动位移响应在整个轴线上均为行波占主导。图6给出了三种不同真实阶梯流剖面下细长柔性圆柱体的无量纲振动位移响应，图7 给出了三种不同真实阶梯流剖面下某个稳态时间段内无量纲振动位移随时间和空间的变化云图。结合图6和图7可明显看出：对于最大流速较小的两种工况（即：Umax=1.5 m/s和Umax=2.0 m/s 时），在结构上端区域（流速较大区域），结构振动位移响应由驻波和行波共同主导；在结构下端区域（流速较小区域），结构振动位移响应则由驻波占主导。而对于最大流速较大的工况（即Umax=2.5 m/s时），结构振动位移响应在沿整个轴线方向上均呈现出行波占主导的特性。

图4 指数剪切流时三种不同最大流速下细长柔性圆柱的均方根、最大位移值以及位移包络线的变化规律Fig.4 RMS,maximum values of the VIV displacements and VIV displacement envelopes of a long flexible cylinder under three different Umax for an exponential shear flow

图5 指数剪切流时三种不同最大流速下细长柔性圆柱的位移随时间（t）和位置（z）的变化规律Fig.5 Displacement evolutions versus time and span location of a long flexible cylinder under three different Umax for an exponential shear flow

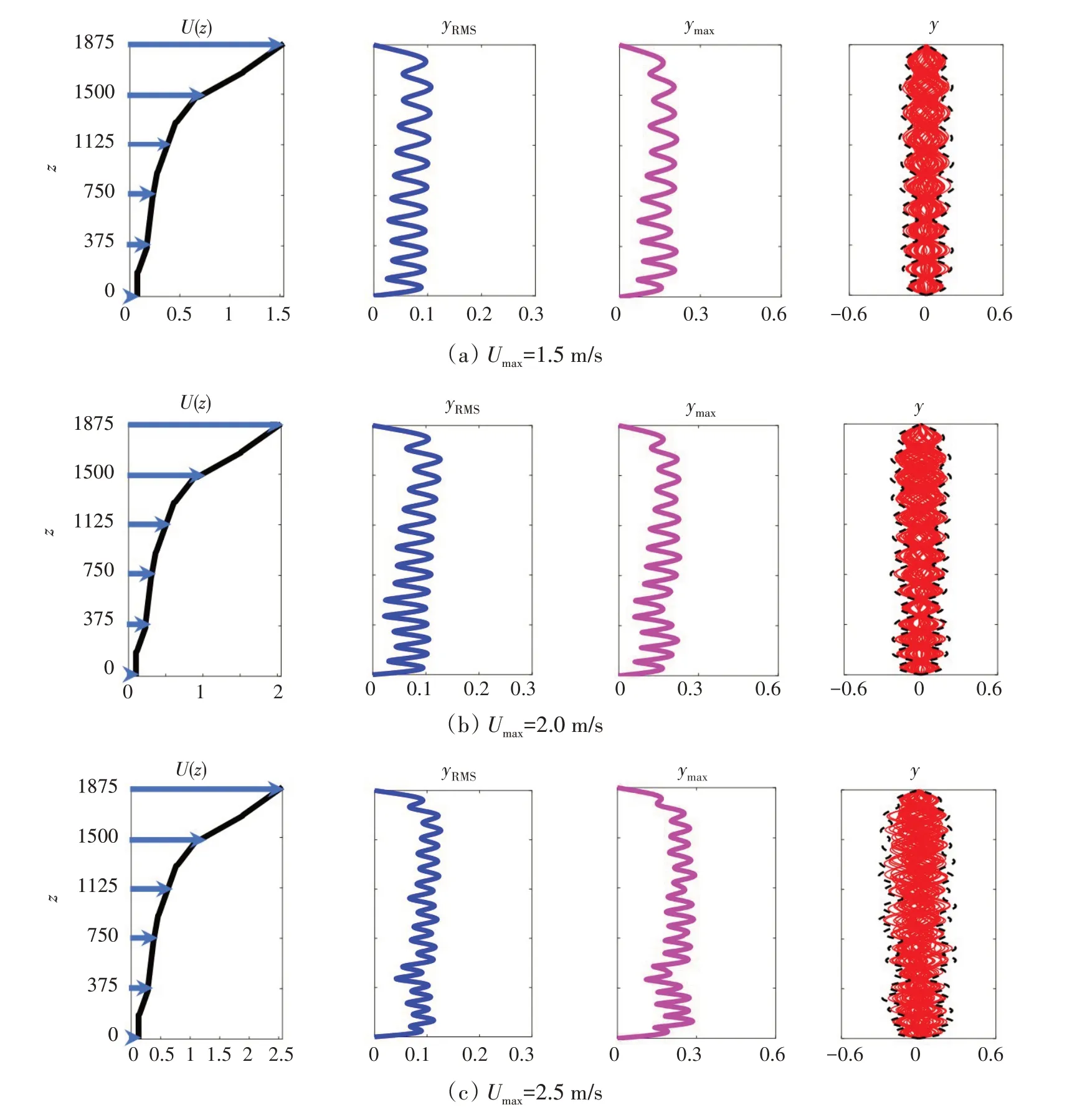
图6 真实阶梯流时三种不同最大流速下细长柔性圆柱的均方根、最大位移值以及位移包络线的变化规律Fig.6 RMS,maximum values of the VIV displacements and VIV displacement envelopes of a long flexible cylinder under three different Umax for a real stepped flow

图7 真实阶梯流时三种不同最大流速下细长柔性圆柱的位移随时间（t）和位置（z）的变化规律Fig.7 Displacement evolutions versus time and span location of a long flexible cylinder under three different Umax for a real stepped flow

综合比较图2、图4 和图6 的第二列可看出：对于某个选定的最大流速，线性剪切流剖面下的结构振动位移响应RMS 值与指数剪切流剖面和真实阶梯流剖面下的结构振动位移响应RMS 值均存在明显的差异。对于同一个最大流速，指数剪切流剖面和真实剪切流剖面下的结构振动位移响应RMS 值非常接近，均比线性剪切流剖面下的结构振动位移响应RMS 值要小很多。由图2、图4 和图6 的第二列同样可以看出：对于某个选定的最大流速，三种不同流剖面下结构振动位移的主导模态阶数非常接近，只有轻微的区别。以Umax=2.0 m/s 为例，当流剖面分别为线性剪切、指数剪切和真实阶梯流剖面时，结构振动主导模态阶数依次为13阶、14阶和14阶。

3.2 结构振动响应的频谱分析

图8～10 依次给出了线性剪切、指数剪切和真实阶梯流剖面下结构的振动位移时间历程曲线、响应幅值谱和相图。值得注意的是，对于每种不同类型的流剖面，分别选取了3 种最大流速（即Umax=1.5 m/s，2.0 m/s，2.5 m/s）加以研究。为了研究方便，这里仅对振动位移RMS 值的最大值加以研究。研究过程中选取的时间段为2000～2500 的振动稳态时间段（如图中的第一列所示），对稳态段振动位移时间历程曲线做快速傅里叶变换便可得到响应幅值谱（如图中第二列所示）；为了更透彻地研究振动位移响应特性，这里进一步对振动位移相图进行了分析（如图中第三列所示）。由图8可看出：当结构处在线性剪切流剖面中时，对于三种不同的流速工况，结构振动均呈现出明显的概周期振动特性；振动响应呈现出明显的宽带分布特性，且存在多个明显的峰值频率；相图轨迹由多个不可重复的椭圆组成，且各个椭圆的中心位置较为接近。

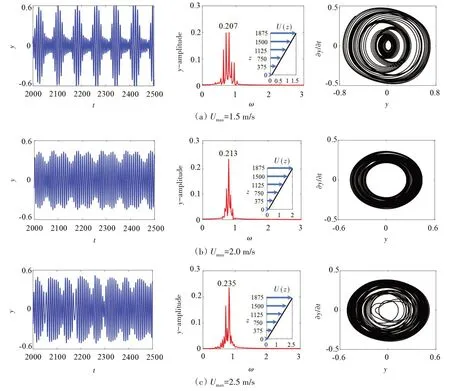
图8 线性剪切流时三种不同最大流速下最大RMS值位置处VIV位移响应的时间历程、振幅谱和相图Fig.8 Time histories,amplitude spectra and phase portraits of the VIV displacement response at the maximum RMS value under three different Umax for a linear shear flow

由图9 可以看出：对于指数剪切流剖面，当Umax=1.5 m/s 时，结构振动呈现出规律的周期性振动特性，结构振动仅存在一个峰值频率，相图轨迹为一系列接近重合的椭圆组成；随着流速的增加，当Umax=2.0 m/s，2.5 m/s时，结构振动呈现出不规则的混乱特性，且振动响应频率分布带非常宽，分布在整个0～1 区间内。与图9 中的线性剪切流剖面相比，类似的地方是相图轨迹均由多个不可重复的椭圆组成，但不同之处在于线性剪切流剖面下相图轨迹中不同椭圆的中心位置较为接近，而指数剪切流剖面下相图轨迹中不同椭圆的中心位置差别很大。由图10 可以看出：当结构处在真实阶梯流剖面时，对于三种不同的流速工况，结构振动均呈现出明显的概周期振动特性。

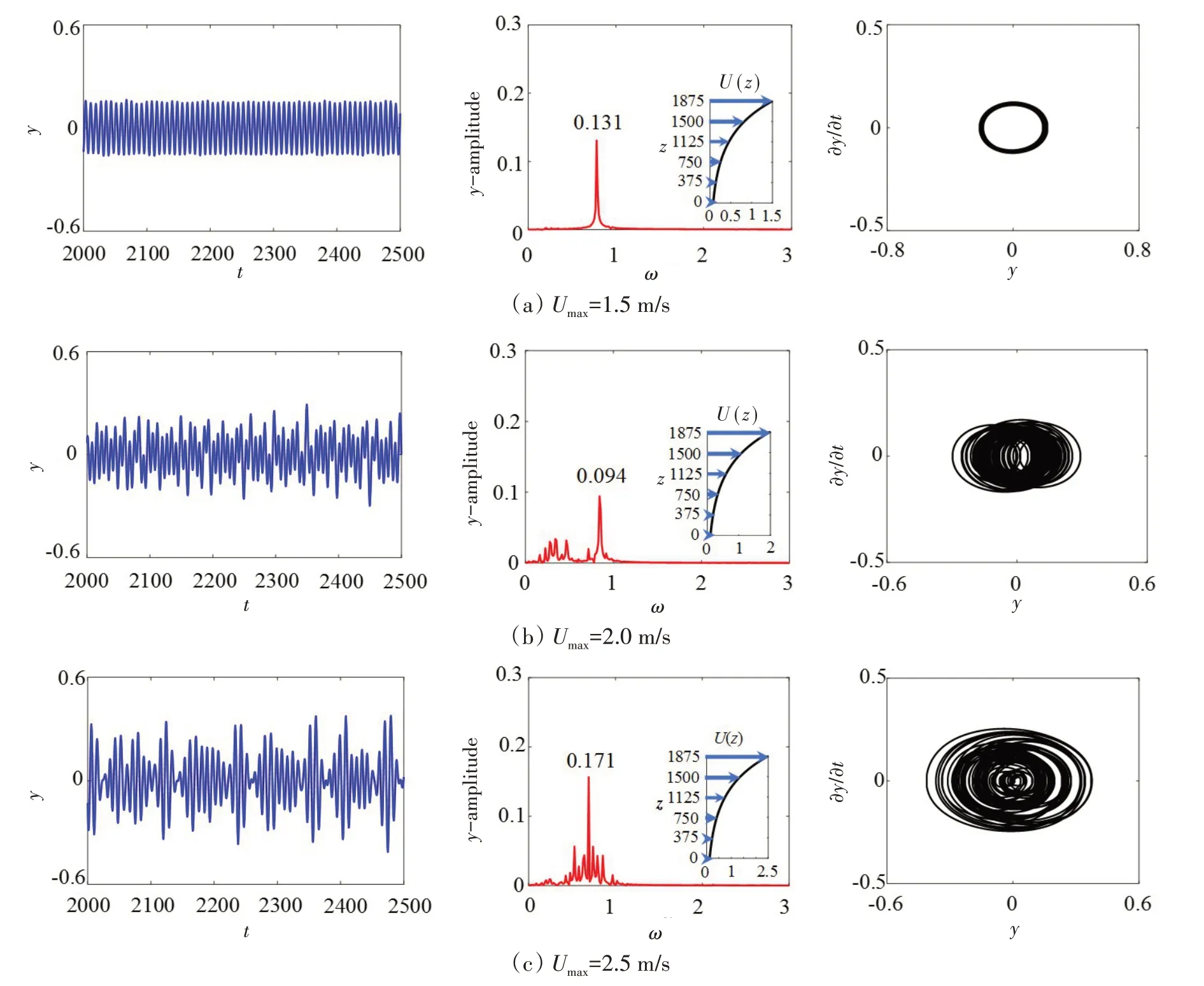
图9 指数剪切流时三种不同最大流速下最大RMS值位置处VIV位移响应的时间历程、振幅谱和相图Fig.9 Time histories,amplitude spectra and phase portraits of the VIV displacement response at the maximum RMS value under three different Umax for an exponential shear flow

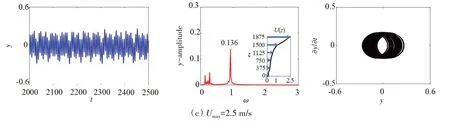
图10 真实阶梯流时三种不同最大流速下最大RMS值位置处VIV位移响应的时间历程、振幅谱和相图Fig.10 Time histories,amplitude spectra and phase portraits of the VIV displacement response at the maximum RMS value under three different Umax for a real stepped flow

4 结 论

本文对三种不同流剖面（线性剪切、指数剪切和真实阶梯流剖面）、三种不同的流速工况（即Umax=1.5 m/s，2.0m/s，2.5 m/s）下的细长柔性结构涡激振动响应特性进行了数值研究。该数值研究可为柔性立管早期的合理设计和服役期间的安全工作提供理论支持和技术保障。基于上述数值研究结果，可以得到如下结论：

（1）对于线性剪切流剖面，在结构两端结构振动位移由驻波主导，而在结构中间区域，结构振动位移则由行波主导；对于指数剪切流剖面和真实阶梯流剖面，随着最大流速的增加，振动位移响应沿整个轴线方向上由驻波主导，但具备轻微行波特性逐渐向完全由行波主导转变。因此，立管设计过程中（尤其在高流速下），要重点关注立管轴线方向上的行波传播对立管涡激振动响应特性的影响。

（2）当使用线性剪切流剖面去预测真实阶梯流剖面时，得到的振动位移响应预测值与真实值存在明显差别，而得到的主导模态阶数预测值与真实值差别不大；当使用指数剪切流剖面去预测真实阶梯流剖面时，得到的振动位移响应预测值以及主导模态阶数预测值均与对应的真实值非常接近。

（3）当使用线性剪切流剖面去预测真实阶梯流剖面时，得到的振动响应幅值以及振动频率分布的预测值均与真实值存在很大差别；当使用指数剪切流剖面去预测真实阶梯流剖面时，得到的振动响应幅值与真实值非常接近，但振动频率分布的预测值与真实值仍存在较大差别。因此，在立管早期设计以及后期分析中，为了保证数值计算结果的可靠性，应尽量使用具有分段表达式的真实阶梯流剖面来进行分析，而不是使用具有单一表达式的简单流剖面来进行分析。