用圆锥曲线焦点弦结论巧算高考题

李兰

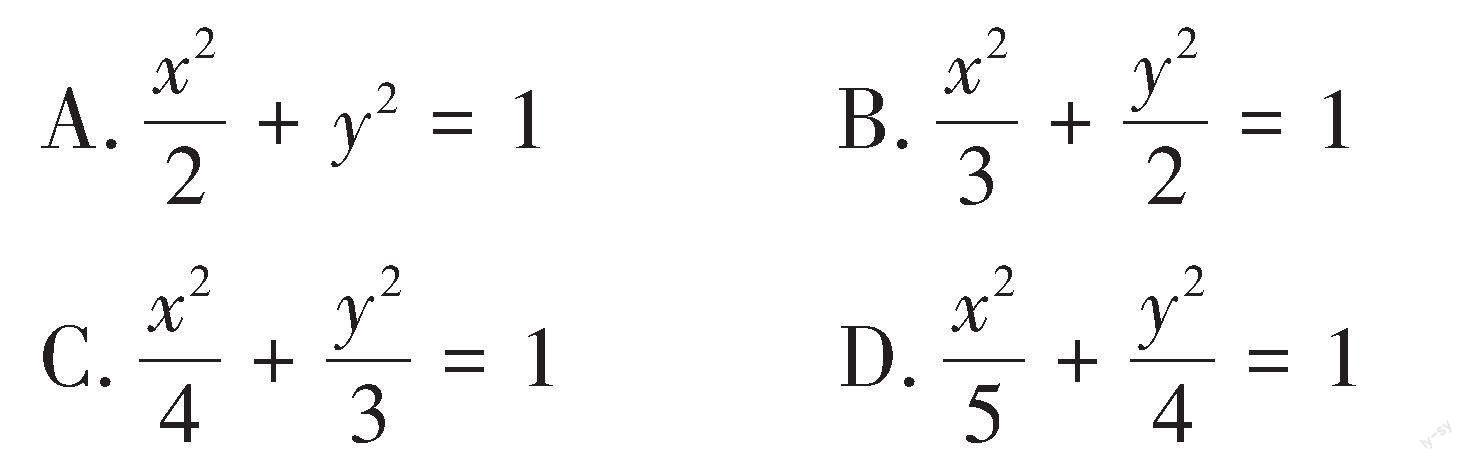
［摘 要］圆锥曲线焦点弦结论具有统一形式，利用焦点弦结论可以快速解决高考题，为考生打开解题思路，提高学生的解题能力。

［关键词］圆锥曲线；焦点弦；高考题

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）17-0024-03

一、公式及其证明

证明如下：

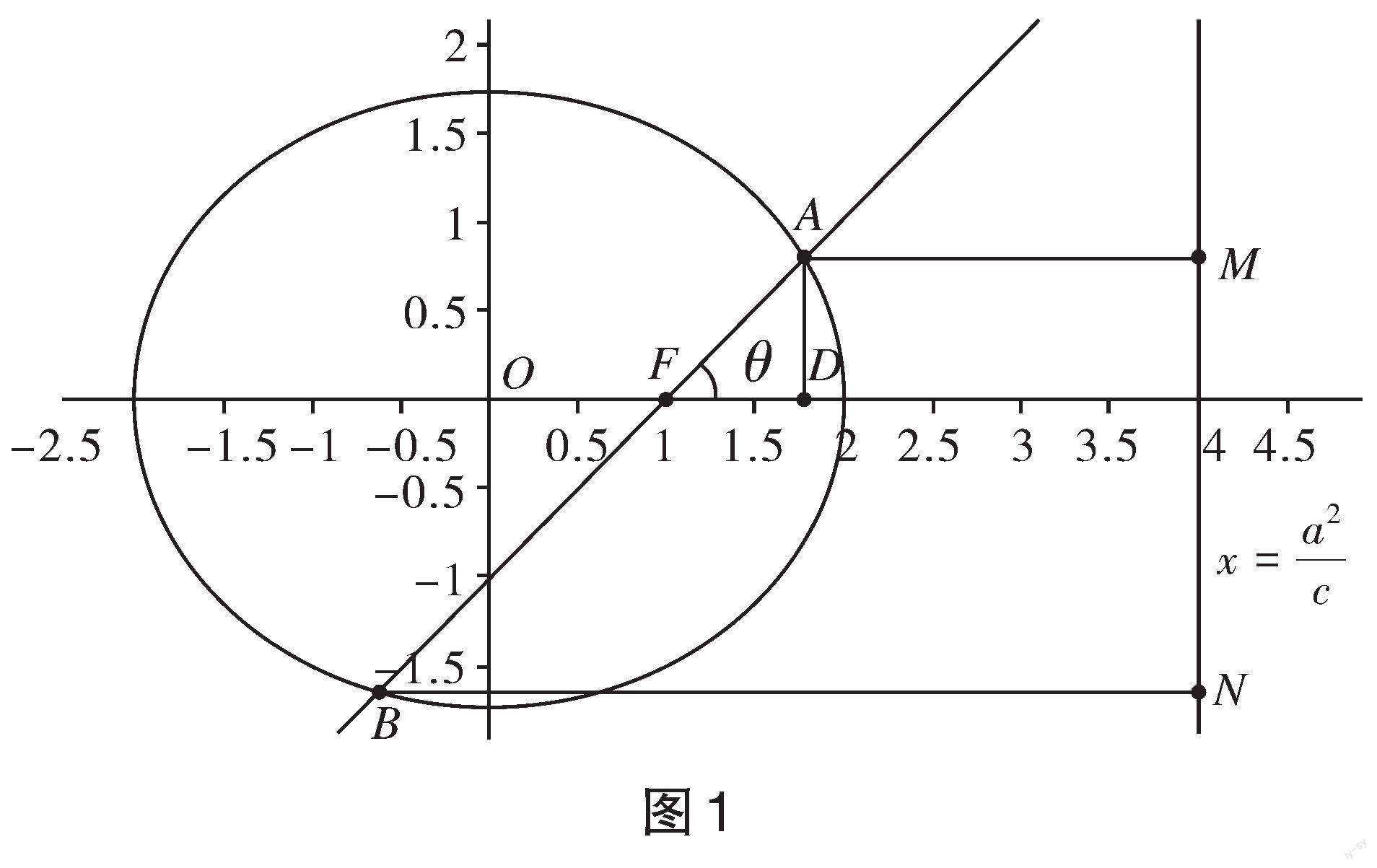
由[A、B]两点分别向右准线作垂线，垂足为[M、N]，由[A]点向[x]轴作垂线，垂足为[D]，由圆锥曲线统一定义，椭圆上点到焦点的距离比到准线的距离等于离心率得

所以[c+AFcosθ=x1]，

二、几个推论

2. [1AF+1BF=2b2a]。

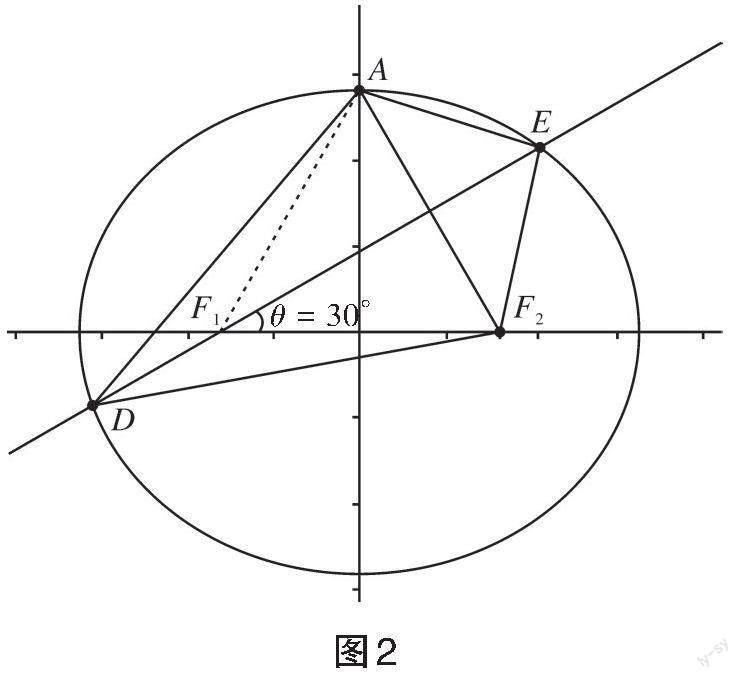
∵[DE⊥AF2]，故[DE]为[AF2]的垂直平分线，

∴[△ADE]与[△F2DE]全等，

∴[C△ADE=C△F2DE=4a=13]。

解法2：

∵[∠EF1F2=30°]，[∠DF1F2=150°]，设[EF1=x]，[DF1=y]，

后续证明同解法1。

解法3：

解法4：

∵[DF1=a+ex1]，[EF1=a+ex2]，即[DE=2a+e（x1+x2）=6]，

结合解法3和解法1，周长为13。

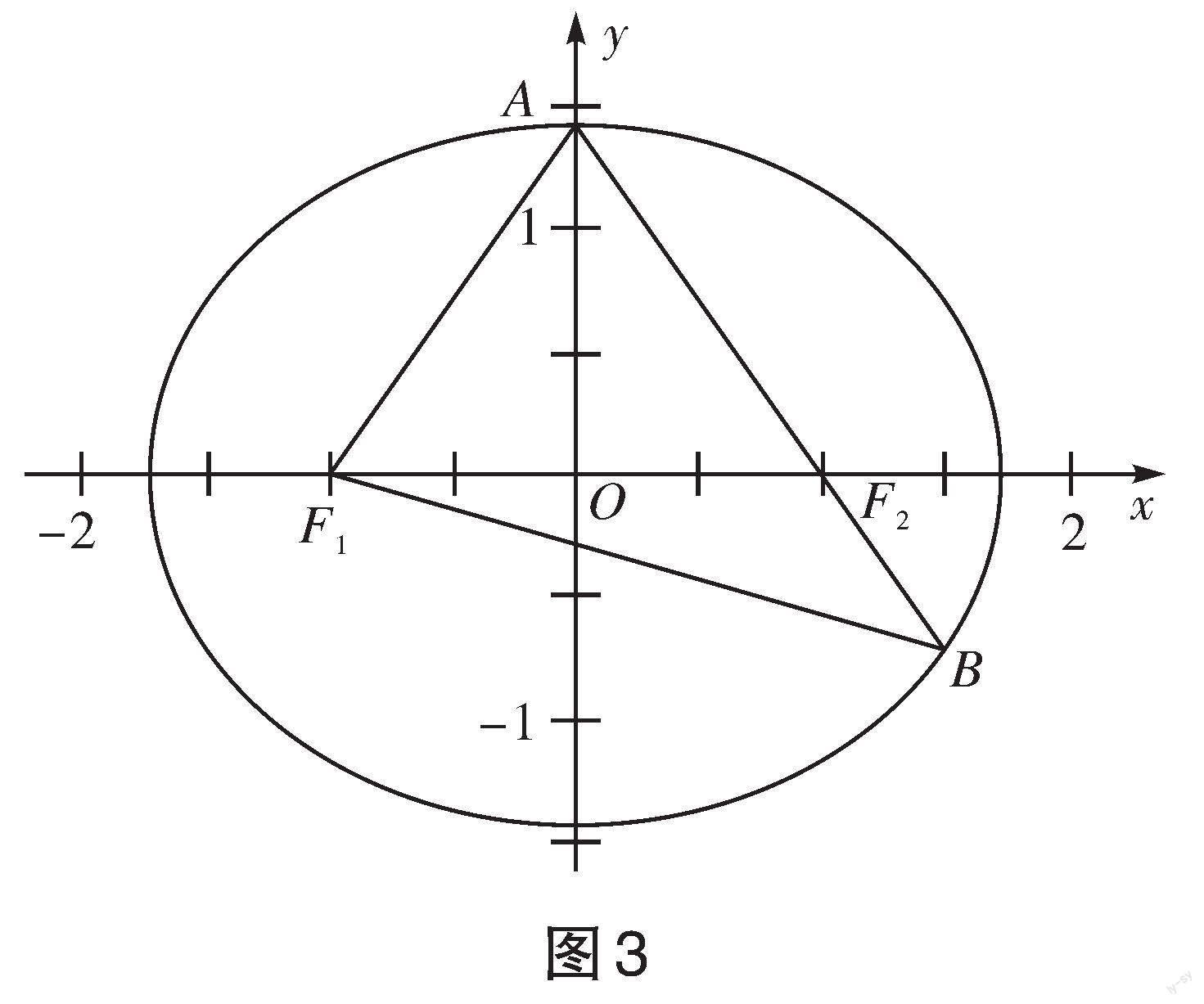
［例2］（2019年高考全国Ⅰ卷第10题）已知椭圆[C]的焦点为[F1（-1，0）]，[F2（1，0）]，过[F2]的直线与[C]交于[A]、[B]两点。若[AF2=2F2B]，[AB=BF1]，则[C]的方程为（ ）。

解法1：

如图3所示，设[BF2=x]，[AF2=2x]，則[BF1=3x]，根据椭圆定义可知，[BF1+BF2=2a]，所以[AF2=a]。

[∴3b2=2a2]，且[c2=1]，∴选B。

解法2：

解法3：

由已知可设[F2B=x]，则[AF2=2x ， BF1=AB=3x]，由椭圆的定义有[2a=BF1+BF2=4x]，所以[AF1=2a-AF2=2x]。在[△AF1B]中，由余弦定理推论得[cos∠F1AB=4x2+9x2-9x22·2x·3x=13]。在[△AF1F2]中，由余弦

解法4：