微型电动汽车电机轴最佳轴承跨距分析
2023-09-20徐劲力陈佳伟
徐劲力,陈佳伟
(武汉理工大学 机电工程学院,湖北 武汉 430070)
EV(electric vehicle)车与传统燃油车在结构方面的差别主要是驱动方式以及传动方式不同,传统燃油车的传动系统主要由离合器、变速器、主减速器、差速器、左右半轴等构成。电动汽车传动形式则大为简化,通常采用电机直接连接减速器再将动力传递至后桥,这种动力布置方式相比于传统燃油车而言,可以使系统结构大为简化,传动链短,传动效率得以提高[1-2]。因此,减速器作为电动汽车的重要组成部分,其性能优劣直接决定着整车的NVH(noise vibration harshness)。
EV车型减速器在传递能量的过程中,必然伴随着零部件的振动。轴承用于支承各类回转零部件,其工作性能的优劣会直接影响减速器的刚度、传动精度、平稳度、承载能力等特性。较好的轴承安装距,能提高传动系统整体的刚度,并保证系统在长时间的运行中不至于因为刚度不足而产生较大形变,进而产生振动影响传动精度和工作效率。Hagiu[3]分析了高速旋转条件下主轴系统轴承预紧力对系统可靠性的影响。邓四二等[4]通过实验的方法对主轴系统中主轴刚度、支撑跨距和系统动态特性进行了相关研究。孙志礼等[5]研究了轴承预紧力和跨距对于主动齿轮的影响,结合Abaqus验证了理论模型的正确性。王世栋等[6]根据齿轮箱模态振型对结构进行了优化。谈聪[7]在Masta中建立了差速器耦合模型,分析了齿轮啮合刚度、激励对振动噪声的影响。郑雅琳等[8]基于传递矩阵的计算方法,研究了主减速器齿轮跨距对传动系统的振动响应,借助ADAMS(automatic dynamic analysis of mechanical systems)进行动态仿真验证。
笔者根据悬臂梁理论推导了最大刚度以及最小挠度的电机轴轴承跨距。在常态工况下,计算得到电机轴轴承的径向刚度,运用牛顿迭代法,结合Matlab计算了电机轴轴承最佳理论跨距,基于ADAMS采用有限元分析法分析了不同跨距下的齿轮啮合特性,研究了电机轴轴承支撑跨距对减速器动态特性的影响。
1 微型电动车减速器模型的建立
微型电动汽车的减速器主要是由电机输入轴、一级主被动齿轮、中间传动轴、二级主被动齿轮、差速器、轴承组成,如图1(a)所示。按照图1(b)的二维尺寸进行UG三维建模并按照要求进行装配。
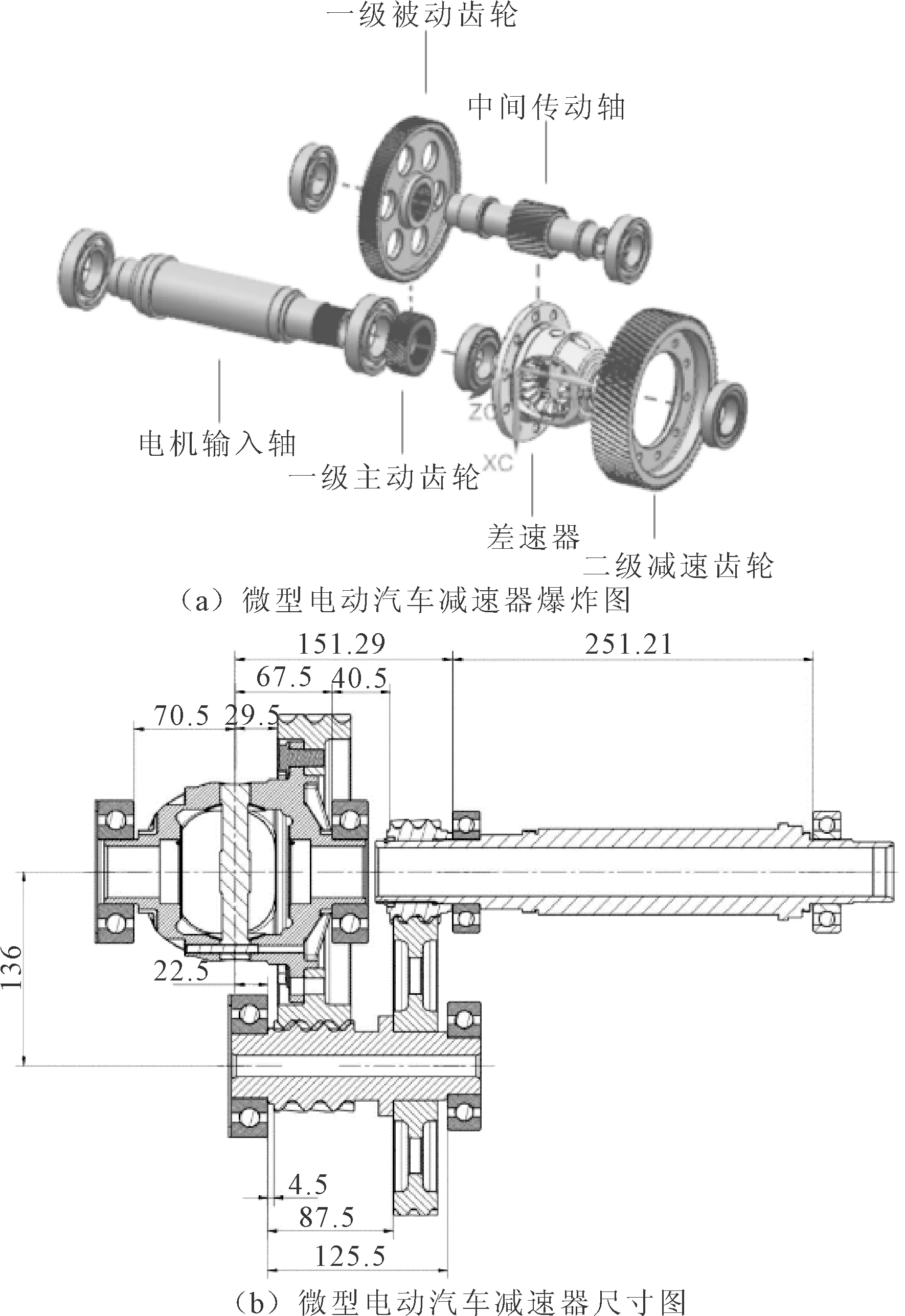
图1 微型电动汽车减速器
在减速器实物中,电机轴上的两个6209轴承实际安装跨距为251.21 mm,它们在调整垫片的压力下紧固在电机轴上。为了提高减速器的传动精度和使用寿命,笔者从理论和ADAMS动力学仿真两方面对电机轴的支撑轴承跨距进行研究,并采用定量的方法对结果进行分析对比。
2 最佳安装跨距理论计算
2.1 轴承最佳安装跨距的计算
将电机轴化简为简支梁,如图2所示,轴端部受到载荷F作用并产生形变δ,根据材料力学[9]可将变形分为刚性支撑下的弹性齿轮变形和刚性齿轮下弹性支撑的形变量之和。
(1)将轴承视为刚性件,齿轮视为柔性件,在这种情况下,可将电机轴看作是一段由轴承-转轴组成的简支梁AB和以齿轮-轴组成的悬臂梁BC,如图3所示。两者受力产生的形变均会引起C点的偏移,而二者的和即为C点的总形变值。

图3 刚性轴承支承和弹性齿轮轴的变形
对于简支梁AB的形变而言,可将载荷平移至截面B处,此时得到截面B在力偶的作用下产生的转角值θB为:
(1)
式中:F为电机轴齿轮所受外力;a为电机轴齿轮的悬伸量;L为轴承跨距;E为电机轴齿轮的弹性模量;I为电机轴齿轮的截面惯性矩。
刚性齿轮的位移量w1可表示为:
(2)
在负载F的作用下,悬臂梁BC在C处引起的形变量w2可以表示为:
(3)
此时在刚性支撑下,柔性齿轮端发生的总形变量δ1可以表示为:
(4)
(2)将齿轮视为刚性件,轴承视为柔性件。弹性轴承支承和刚性齿轮轴的变形如图4所示。在这种情况下,将支撑轴承视为弹性体,则轴承和轴将发生较小的位移,满足弹性变形的条件,此时变形可认为是线性的。因此,在两轴承处产生的支反力作用下的位移变形量y1和y2分别为:
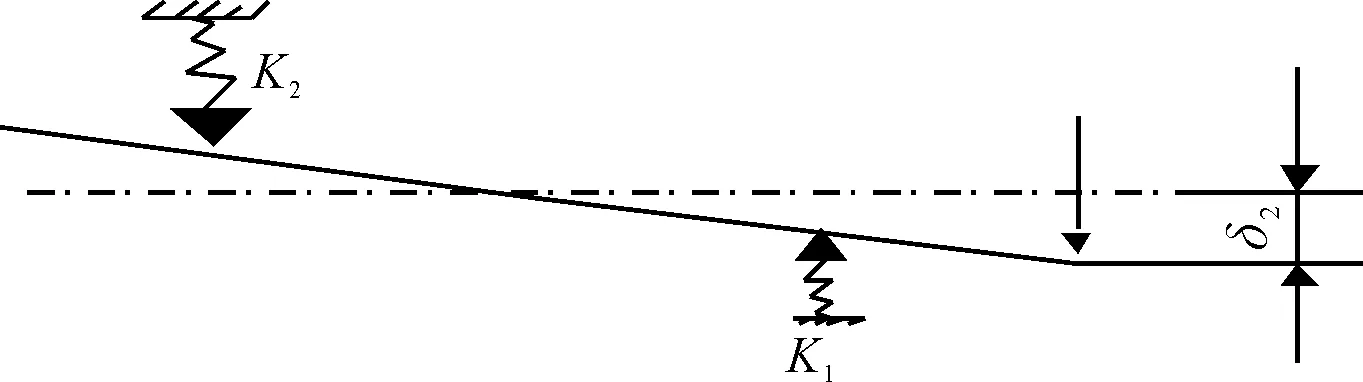
图4 弹性轴承支承和刚性齿轮轴的变形
y1=R1/K1,y2=R2/K2
(5)
式中:K1、K2为左右两个轴承的径向刚度。R1、R2为作用在左右两个轴承上的支反力。
此时电机轴一级主动齿轮处的位移量δ2为:
(6)
(7)
根据结构力学相关知识,可以得到电机轴齿轮端在啮合力作用下的综合挠度δ为:
δ=δ1+δ2
(8)
式(8)表达了电机轴齿轮啮合力、轴承刚度以及悬伸量之间的关系,电机轴齿轮的最佳安装距的取值应设置在系统刚度最大,而挠度最小的时候。因此对式(8)进行求导处理,可得电机轴轴承最佳的安装跨距L0为:
(9)
整理后得到
(10)
式中,K为6209轴承的径向刚度。
利用判别式法可知,上述方程仅存在一个实根。引入中间变量m,设m=6EI/K,则式(10)可进一步化简为:
(11)
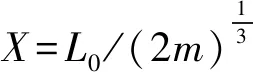
X3-XY-1=0
(12)
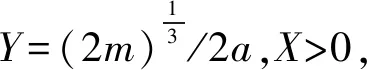
(13)
由于牛顿迭代法在方程的单根附近具有平方收敛速度,此处笔者利用牛顿迭代法的思想对X的数值进行求解。
对于式(13),判断其敛散性,因Y恒大于0而X恒大于1,故谱半径恒小于1,即迭代式(13)收敛。
2.2 轴承支撑刚度计算
为了计算出电机轴轴承安装的最佳跨距,除了要取得材料属性和受力条件外,还需要计算出6209轴承的径向刚度。
滚动轴承的刚度定义是:在负荷方向上轴承内外圈产生单位的相对弹性位移量所需要的外加负荷。轴承刚度R的表达式为:
R=dF/dδ
(14)
式中:F为轴承的径向、轴向负荷或力矩;δ为轴承在力和力矩作用下产生的弹性位移量。
轴承的变形计算是以赫兹接触理论为基础进行的,在自由状态下,6209深沟球轴承的滚动体和内外滚道接触产生的形变量δ为[10]:
(15)
式中:a为轴承接触角;Qmax为受载最大的滚动体载荷;Dw为滚动体直径。
Qmax=5Fr/Zcosa
(16)
式中:Fr为轴承径向力;Z为滚子个数。
则电机轴轴承径向刚度K为:
K=1 190×(DwFrZ2cos5a)1/3
(17)
根据企业测试结果,在电机常态工况3 200 r/min下,轴承所受径向力为45 kN,6209轴承的其它参数如表1所示。

表1 6209轴承参数
将参数代入式(17)可计算出电机轴6209轴承的径向刚度K为558 168.45 N/mm。
2.3 最佳跨距计算结果
将轴承刚度计算结果代入跨距L0的迭代公式(13)中进行计算,得到m=48 881.9;n=3 715 020.7;Y=2.037 9。
利用Matlab软件完成多次迭代计算,迭代初值设置为X=1.1。关键代码如图5所示。
通过多次迭代,X的值稳定1.628,迭代结果如图6所示。通过式(11)和式(12)可以计算出电机轴轴承最佳安装跨距为L0=252.2 mm。
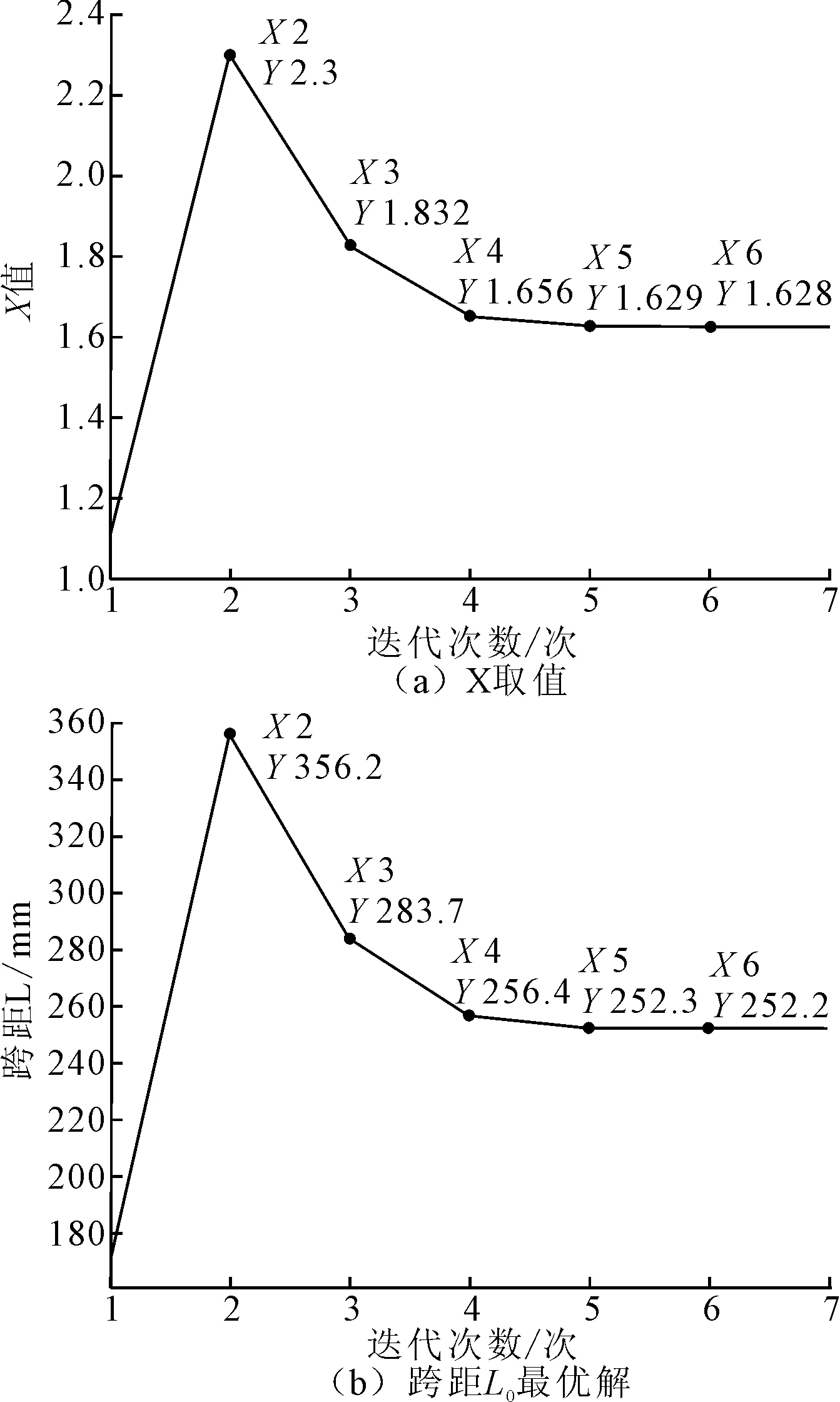
图6 数值分析X和电机轴轴承最佳跨距值
3 微型电动汽车模型的仿真分析
通过理论计算可知,电机轴轴承在252.2 mm时,电机轴挠度最小,刚度最大。对微型电动汽车整体模型进行仿真分析,取跨距为250.2 mm、251.2 mm、252.2 mm、253.2 mm的4组参数进行定量分析,其它部件的尺寸和安装匹配关系不变。将UG绘制的三维模型(如图7)导入ADAMS中进行分析。根据EV车实际工作车速范围,给电机轴施加2 600 r/min、3 200 r/min、3 600 r/min和4 400 r/min的驱动转速,并在差速器输出半轴施加恒定负载转矩500 N·m。仿真并分析电机轴轴承跨距的改变对一级齿轮啮合的振动影响。

图7 微型电动汽车桥架UG模型
3.1 仿真前处理
所研究的EV车型的相关材料参数如表2所示。轴承等零件的相关参数设置和齿轮接触副设置如图8所示。
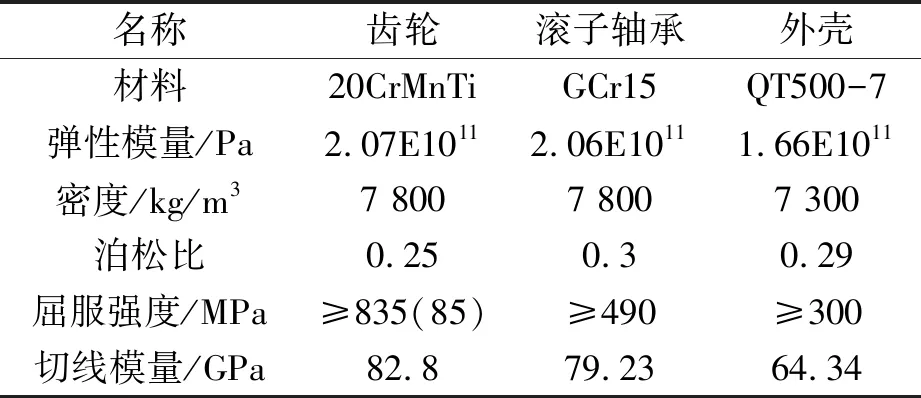
表2 减速器部件的材料参数
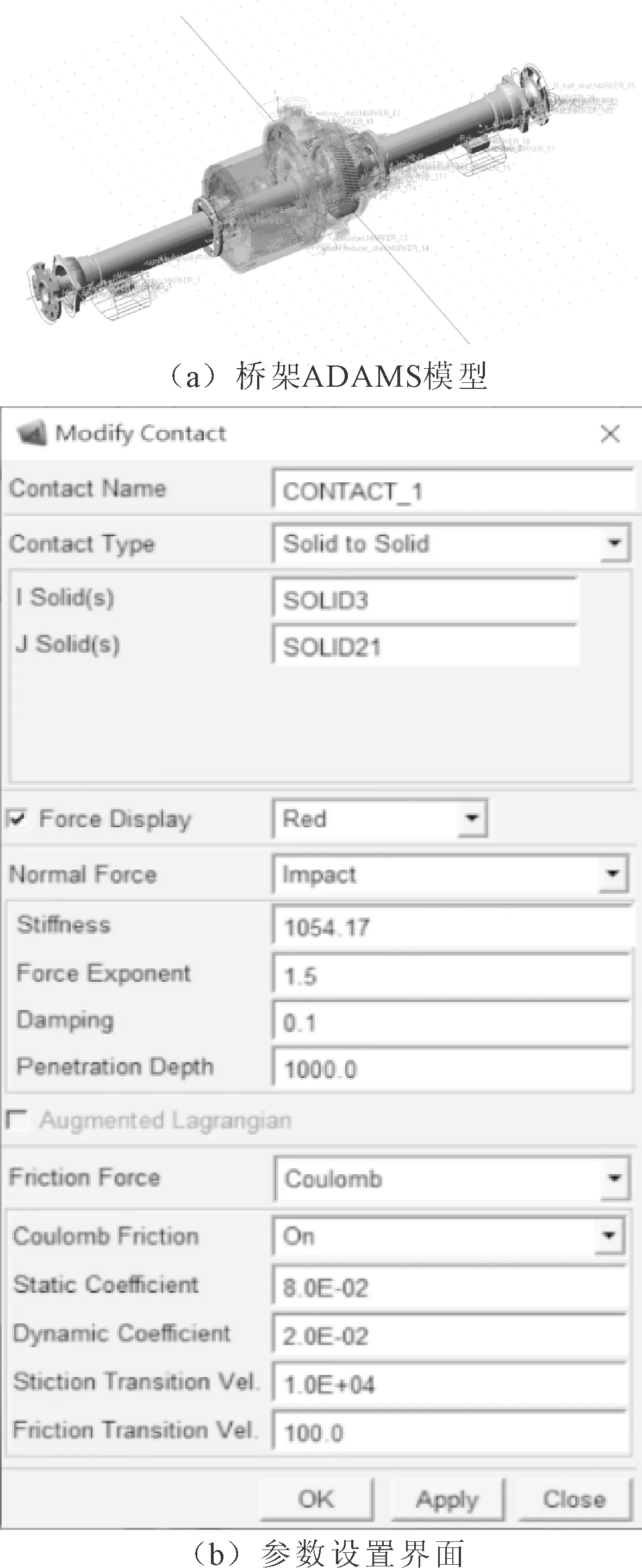
图8 ADAMS模型及参数设置
3.2 仿真结果分析
对于汽车乘坐者而言,垂直地面的振动是最为敏感的,因此将Y方向振动作为研究的重点。不同跨距下齿轮Y向振动位移的均方根值如图9所示;不同跨距下一级齿轮啮合力均值如图10所示。从图9可知,模拟电机3 200 r/min常态工况,电机轴轴承跨距的变化对于二级齿轮Y向位移影响较小。而在跨距取252.2 mm时一级齿轮Y向振动幅值最小。从图10可知,当电机轴轴承跨距为252.2 mm时,一级齿轮啮合力是最小的,系统更加平稳。
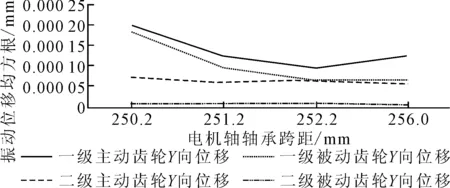
图9 不同跨距下齿轮Y向振动位移均方根值

图10 不同跨距下一级齿轮啮合力均值
4 结论
研究表明,电机轴轴承安装跨距对于整车的振动幅值有影响,通过理论计算和仿真分析,针对所研究的EV车型,当电机轴轴承跨距调整到252.2 mm时,电机轴的挠度最小,刚度最大,此时减速器中一级齿轮Y向的振动幅值相对较小,可以提高EV车的舒适性。
