基于区间q阶正交模糊集的应急供应商选择方法研究

高玉集,郭 钧

(武汉理工大学 机电工程学院,湖北 武汉 430070)

为了在复杂多变的国内外环境下寻求平稳发展,许多制造企业都在突发状况发生时,选择应急供应商临时供货来维持企业的正常生产[1]。

在应急供应商选择问题中,Esmaeili等[2]在考虑供应中断风险和紧急情况的基础上,提出了混合整数非线性规划模型,求解集中式供应链应急供应商选择问题。Olanrewaju等[3]考虑了自然灾害导致的供应链中断情况,提出了多阶段随机规划模型以解决灾难响应情形下的应急供应商选择问题。Wang等[4]构建了基于不完全异构信息的基于距离的VIKOR(visekriterijumska optimizacija I kompromisno resenje)多属性群决策方法,解决了技术导向型企业的应急供应商选择问题。张梦玲等[5]对突发事件发生时不确定需求下的政府应急采购的供应商选择问题展开研究,并为此提出基于L1范数的两阶段鲁棒优化模型。

在决策模型方面,区间q阶正交模糊集[6](interal-valuedq-rung orthopair fuzzy set, IVq-ROFS)能提供更为广阔、灵活的偏好决策空间和更高的模糊信息表达能力,不确定语言集[7](uncertainty linguistic term set, ULTS)是模糊环境的常用的不确定定性表达方式。犹豫度模糊熵[8]能描述模糊集的模糊程度和模糊信息的可靠性,BWM(best worst method)法[9]仅需要较少的比较次数就能获得良好的结果,故而常被用于信息受限时的权重确定内容。基于距离的组合评价方法[10](combinative distance-based assessment, CODAS)利用欧式距离和汉明距离衡量方案总体表现,被用于复杂环境下的供应商选择问题。

为此,笔者构建一个专家和属性权重未知情形下的高度不确定的多属性群决策模型。首先,决策者使用IVq-ROFULS(interal-valuedq-rung orthopair fuzzy uncertain linguistic set)定性地表达待选应急供应商的各种属性间的评价信息。其次,决策者使用IVq-ROFULS表达各属性间的重要性的不确定模糊评价并借助BWM确定属性权重。再次,通过各个专家的评估内容的犹豫度来确定客观专家权重,即通过犹豫度区间q阶正交模糊熵求解专家权重。最后,采用CODAS方法用来抉择最终的应急供应商。

1 基于CODAS和BWM的区间q阶正交模糊语言集多属性群决策模型

在区间q阶正交模糊不确定语言环境中引入BWM方法和犹豫度模糊熵,并借助CODAS方法进行最终的排序决策,构建一个基于BWM和CODAS的区间q阶正交模糊不确定语言集的多属性群决策模型来求解工程机械制造企业的应急供应商选择问题,本模型的主要流程如图1所示。

图1 应急供应商选择流程图

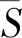
(1)

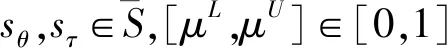
假设K={k1,k2,…,km}为m个潜在的供应商,C={c1,c2,…,cn}为用于评价预定的n个属性,D={d1,d2,…,dr}为r个专家,wD=(wd1,wd2,…,wdr)T为专家权重,W=(w1,w2,…,wn)T为属性权重。

1.1 IVq-ROFULS-BWM计算属性权重

BWM方法首先由决策者确定最优和最劣的准则,然后将其他准则和这两个最优最劣准则依次进行比较,便能得到两组有关偏好的向量,它具有要求比较次数少、结果可靠性高、灵活性高等优点。笔者将BWM推广到区间q阶正交模糊不确定语言环境中去,以计算最佳的属性权重。

步骤2采用IVq-ROFULS给出最佳指标相对于其他指标的偏好:

(2)

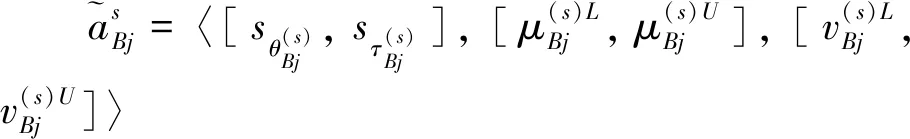
步骤3采用IVq-ROFULS给出其他指标相对于最劣指标的偏好:

(3)

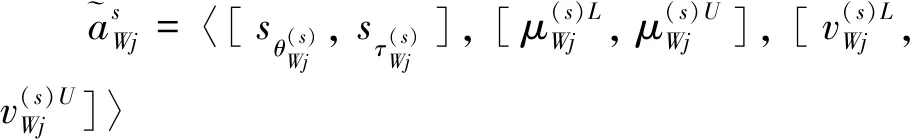
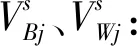
(4)

(5)

步骤5求解非线性规划模型,得到属性权重。

目标函数: minξ

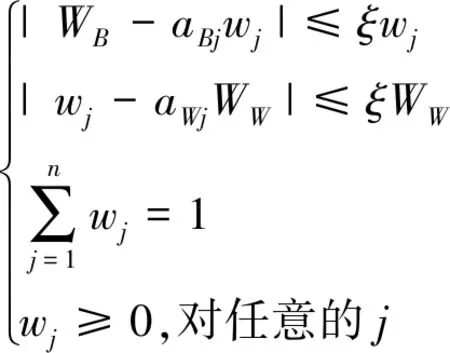
(6)

式中:ξ为属性权重的一致性比率,ξ值越小,则表明一致性越高,即所求解的属性权重的误差越小;WB为最优属性权重值;WW为最劣属性权重值;aBj、aWj分别为决策者做出的第j个指标相对于最优、最劣指标的区间q阶正交模糊不确定语言偏好评价。

1.2 构建基于IVq-ROFULS的决策矩阵

1.3 犹豫度区间q阶正交模糊熵获取专家权重

采用基于犹豫度的区间q阶正交模糊熵来计算专家权重,专家评价过程越不确定,模糊程度越大,则评价信息可靠性越低,也就意味着专家权重越低。计算步骤如下:

(8)

步骤2根据模糊熵大小确定专家权重wds。

(9)

式中:r为专家个数;Es为专家ds的总体区间q阶正交模糊熵。

1.4 CODAS方法对应急供应商选择排序

CODAS方法使用欧式距离作为主要度量依据,如果两个备选项之间的欧式距离非常接近,那么则使用汉明距离作为后续的比较度量参照。应急供应商选择排序步骤如下:

步骤1采用WAA(weighted average operator)聚集算子聚集决策矩阵。

(10)

步骤2利用区间q阶正交模糊不确定语言得分函数计算得分矩阵。

(1+(μU)q-(υU)q)]

(11)

步骤3对得分矩阵加权处理。

(12)

式中:sij为待选供应商i相对于指标j的得分;wj为采用IVq-ROFULS-BWM法计算的属性权重。

步骤4确定负理想解并求解欧氏EDi和汉明距离HDi。

ns=[nsj]=[minivij]1×n

(13)

步骤5构建相对评估矩阵HR。

HR=[hik]n×n=[(EDi-EDk)+

(ψ(EDi-EDk)×(HDi-HDk))]

(14)

其中ψ是用于识别两个备选项的欧氏距离相等的阈值函数,由下面的函数确定:

(15)

式中:τ是由决策者自我设置的阈值参数,取值一般在0.01～0.05之间,即如果两个备选项之间的欧式距离小于τ,那么就可以视为两种的距离的相近,辅助以汉明距离进行比较。

步骤6计算得分函数并排序。

(16)

2 案例分析

2.1 问题描述

来自企业内部技术部、财务部、采购部和生产部的4位专家D={d1,d2,d3,d4}对4个应急供应商K={k1,k2,k3,k4}进行选择决策。决策委员会决定了6个需要纳入评价的指标。它们分别是:运输时间C1,服务态度C2,生产规模C3,产品质量C4,准时交货C5和废物处理C6。

2.2 决策过程

步骤1采用IVq-ROFULS-BWM方法求属性权重。4位决策者首先从自我角度给出最优和最劣的指标,结果如表1所示。然后,采用IVq-ROFULS的评价形式分别给出最优指标相对于其他指标的偏好和其他指标相对于最劣指标的偏好。求解偏好得分如表2所示。根据所有决策者的偏好得分矩阵,构建一个非线性规划函数模型,用于求解最优属性权重。将该模型带入MATLAB求解,可得最优的属性权重为:W=(0.18,0.11,0.15,0.21,0.25,0.11)。

表1 各决策者最优最劣指标

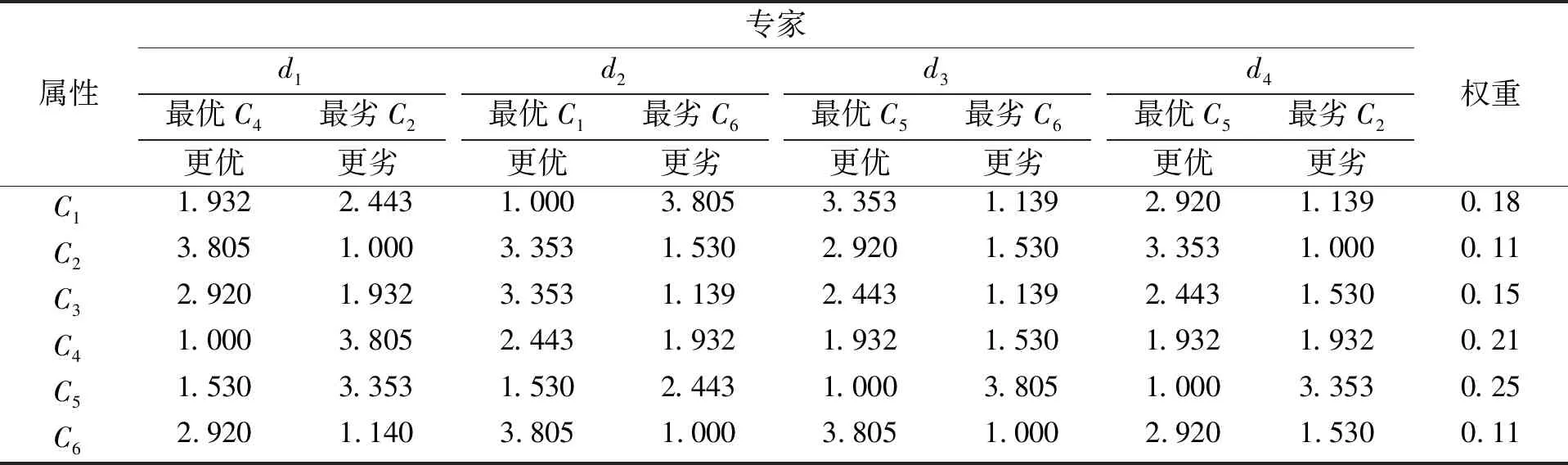
表2 最优和最劣指标偏好得分矩阵

目标函数 minξ

步骤2构建并处理IVq-ROFULS。每一位决策者给出自己对于不同供应商的C1～C6属性。并采用标准化公式标准化初始决策矩阵。

步骤3采用犹豫度计算公式计算专家每次决策的犹豫度,结果如表3所示,表4为区间q阶正交模糊熵矩阵。根据模糊熵的大小确定专家权重为:wD=(0.23,0.24,0.26,0.27)。

表3 专家决策犹豫度矩阵

表4 区间q阶正交模糊熵

步骤4CODAS方法对应急供应商选择排序。采用IVq-ROFULWA(interval-valuedq-rung orthopair fuzzy uncertain linguistic weighted averaging)聚集算子集成标准化后的决策矩阵为群决策IVq-ROFULS矩阵。表5为采用得分函数公式计算各指标相对于各供应商之间的得分情况。对得分矩阵加权处理得加权归一化得分矩阵,如表6所示。确定负理想解为:ns=(0.088,0.022,0.069,0.144,0.034,0.020)。确定各个解之间的欧式距离EDi和汉明距离HDi,结果如表7所示。构建相对评估矩阵,如表8所示,其中阈值参数τ的取值为0.02。利用得分函数和相对评价矩阵计算各个待选供应商之间的得分情况,S=(0.179,0.094,0.000,-0.273),k1便是最优应急供应商选项。

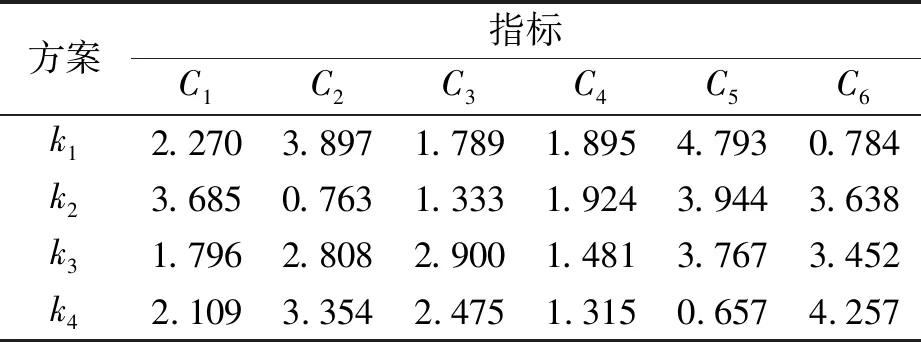
表5 IVq-ROFULS的评价得分矩阵

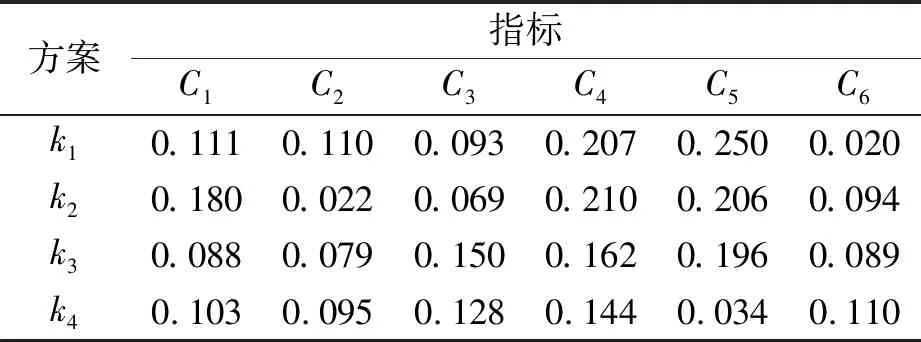
表6 加权归一化评价得分矩阵

表7 欧氏距离和汉明距离

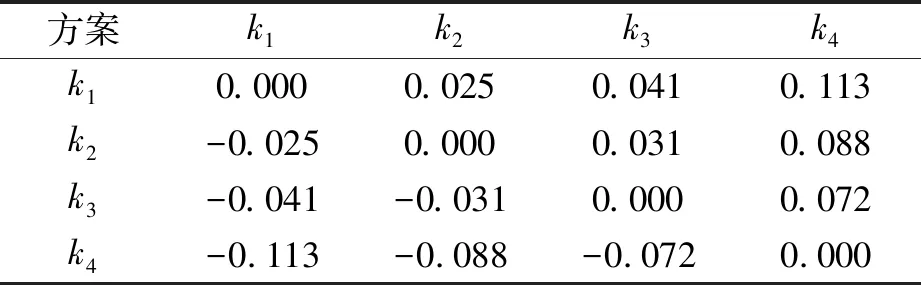
表8 相对评估矩阵

3 讨论分析

3.1 有效性分析

对于多属性决策问题, 哪怕采用的是同样一组实验数据,利用不用的决策方法都有可能会产生不同的排名[11]。Wang等[12]建立了3个测试标准来测试多属性决策方法的相对性能,分别是:①相对重要性保持不变;②可传递性;③子集排序一致性。

(1)针对有效性测试标准1的验证。从得分S可知,k1是最优秀的应急供应商,k2是非最优方案,k3是一个更差的方案,根据测试标准1的要求,本节将标准化后的IVq-ROFULS评价矩阵中所有决策者关于k2和k3的评价信息对调,建立用于测试有效性的测试标准1的决策矩阵。并依照步骤4重新开始计算,得新的加权归一化评价得分矩阵,如表9所示,对于该测试矩阵,继续执行步骤4中剩下的流程。最终测试矩阵对于各个待选供应商的得分情况分别为S=(0.179,0.000,0.094,-0.273)。那么最终的排序结果为k1>k3>k2>k4,最优结果为k1。

表9 有效性标准1加权归一化评价矩阵

基于表9的测试矩阵,得到的应急供应商选项仍是k1,这便验证了标准1。

(2)针对有效性测试标准2和标准3的验证。考虑到测试标准2的要求是验证排序结果的传递性,故借助验证标准3的同时一起验证标准2。首先,将其分解为3个较小的子问题,重复运算步骤,可分别得各个子问题的得分分别为:S=(0.023,0.007,-0.030),S=(0.143,0.052,-0.195)和S=(0.171,0.045,-0.216),可见,这结果与原始未分解的问题的排名结果是一致的,方法在测试标准2和测试标准3下是有效的。

3.2 灵敏度分析

本节将探讨IVq-ROFULS中q和欧式距离阈值参数τ对决策结果变化的灵敏度,为了反映参数q和τ对结果的影响,分别固定q或τ继而探讨τ或q对结果的影响。不同q值对结果的影响如表10所示。不同的τ值对结果的影响如表11所示。

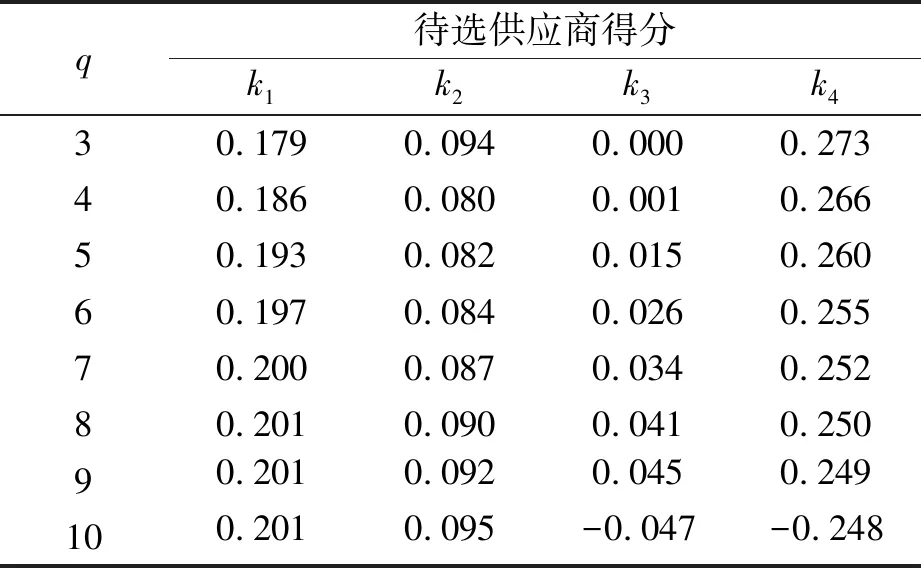
表10 不同q对应的计算结果(τ=0.02)

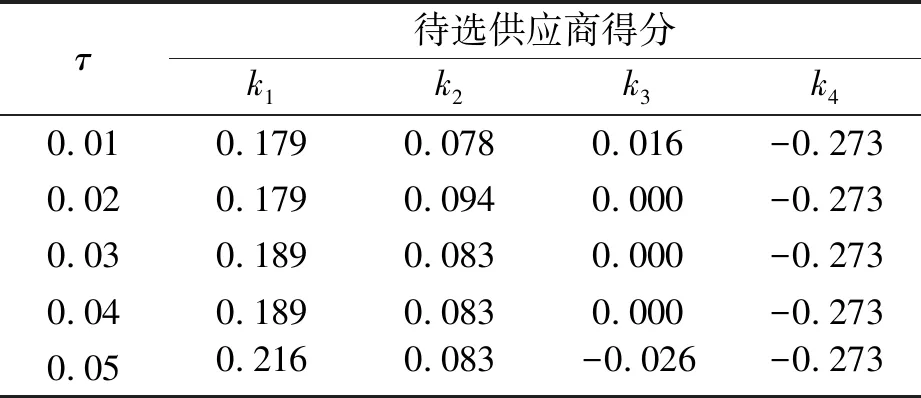
表11 不同取值的τ对应的计算结果(q=3)

4 结论

笔者提出了一个基于BWM和CODAS的区间q阶正交模糊不确定语言集的多属性群决策模型,用于解决在信息受限、复杂环境情形下的短期多属性群决策问题。并借助一个应急供应商选择案例,分析论证了所提方法的可靠性和稳定性,并对结果进行了有效性分析和灵敏度分析。本文方法在保证决策结果有效的情况下兼顾了决策过程的灵活性。