基于多段汉克尔变换拟合的地震干涉算法研究
2023-09-20阮杨帆岳子冲万幸源刘宏岳
周 晓,喻 颜,阮杨帆,岳子冲,万幸源,刘宏岳
(1.武汉理工大学 机电工程学院,湖北 武汉430070;2.福建省建筑设计研究院,福建 福州 350001)
地球表面无时无刻都存在一种人类无法感知的微弱振动。这些微弱振动产生的信号叫微动信号[1]。微动勘探技术就是通过微震台阵观测,以平稳随机过程理论为依据,从微动信号中提取面波(Rayleigh波)频散曲线,通过对频散曲线的反演,从而推断地下结构的一种方法[2]。微动勘探技术以其无需人工源、抗干扰能力强、分辨率高、便捷环保等优势,在城市建设和地下空间开发等领域发挥重要作用。
在工程微动勘探技术中提取面波频散信息常用的方法有空间自相关法(spatial auto-correlation,SPAC)[3]和频率-波数法(frequency wavenumber,F-K)[4]。地震干涉法[5](seismic interferometry,SI)是近年来地球物理研究的一个热点,其理论提出较早,但是并不统一,后续学者有从波动互易、模式均分、时间反转和稳相近似等不同角度对地震干涉法进行了证明和解释[6]。目前有学者已经证明SI法与SPAC法其物理本质是一致的[7-8],SPAC法是在时间域中的描述,而SI法是在频域中的描述。
这3种频散曲线的提取方法各有优劣。SPAC法在数据分析上较为简单,但是对于台阵布置要求严格不能设置为线性排列系统,常用多重圆形台阵,生产作业中受到地理条件的制约较大[9]。F-K法对于台阵摆放要求低,但F-K法提取的频散曲线反映的是台阵下方区域的平均效应,在同样的测量精度下,需要使用更多的检波器。SI法计算的是两个检波器路径间的平均效应,在同等数量检波器下,SI法可以得到地表下方地质结构的更多频散信息,覆盖的勘探区域更加全面。对于地下结构的二维剖面探测,SI法只用沿测线将检波器布置成直线阵列,而SPAC法和F-K法往往需要沿测线布置多个检测台阵或者采用沿测线平移台阵多次测量的方式[10]。因此,SI法可以使用更少的检波器和更短的时间完成勘探任务,极大增加了工作效率,应用前景更加广泛。
笔者研究频率域下两两台站微动信号间求解面波相速度的地震干涉算法,针对传统的贝塞尔函数拟合一般只使用单调递减部分的相干系数[11],提出一种基于汉克尔变换分段的方法,能够有效地把相干系数划分为不同的单调区间段,分段拟合贝塞尔函数求解面波相速度,解决相速度频散曲线高频范围缺失、探测盲区深度较大的问题。
1 方法原理
1.1 地震干涉算法原理
干涉在物理学中指的是两列及其以上的波空间中相遇发生叠加形成新的波。地震干涉法是基于两个检波器记录的微动信号,其核心思想是通过互相关理论计算出两个信号间的经验格林函数。当噪声源随机分布时,表征噪声源与波场关系的经验格林函数符合真实的格林函数。
对于单一经验格林函数,可以通过地震干涉结果频谱实部拟合零阶第一类贝塞尔函数,来求解Rayleigh波相速度频散信息[12]。
根据Yokoi等[7]在证明SPAC法与SI法的一致性中推导的理论公式,地震干涉法两两之间的互相干函数满足:
γA,B=J0(krA,B)
(1)
式中:γA,B为A、B台站垂直方向微动信号的互相干函数;r为A、B台站之间的距离;k为波数;J0为第一类零阶贝塞尔函数。
在频率域中,两道信号地震干涉法的互相干计算公式为:
(2)
式中:uA、uB为A、B两点信号的傅里叶变换;*为复数共轭;|·|为复数的模。
结合式(1)、式(2),有:
(3)
根据式(3)相干系数拟合贝塞尔函数,可求出频率为f时,对应的波数k,相速度满足c=2πf/k,即可求出两道微动信号的瑞雷波相速度频散曲线。上述公式推导适用于以基阶瑞雷波能量为主,利用垂直分量观测数据,提取面波频散曲线的情况。对于水平分量观测数据则不适用。
1.2 多段汉克尔变换分段原理
汉克尔变换[13]是一种积分变换,又称作傅里叶-贝塞尔变换,是由数学家Hankel提出的。对给定核函数f(r),以v阶第一类贝塞尔函数Jv(kr)作无穷级数展开,级数的各项k变化,各项Jv(kr)前的系数Fv构成了变换函数,就是一种v阶汉克尔变换。k为自变量,把连续函数Fv(k)在(0,∞)上表示为:
(4)
地震干涉法在估算瑞雷波相速度频散曲线时,传统的贝塞尔函数拟合方法只使用了单调递减部分相干系数,而震荡衰减部分的相干系数没有被利用,对应的有效频率范围集中在低频区间,高频数据缺失,反映在深度上即浅层数据缺失,探测盲区大。笔者利用汉克尔变换,把地震干涉法提取的相干系数γ(f)作为核函数,其零阶第一类贝塞尔函数的汉克尔变换为:
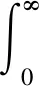
(5)
当k>ks(ks为控制参数,通常取ks=0.15),并且F(k)取得最大值时,对应的k=ξ,在满足这个条件下,拟合的贝塞尔函数效果最佳,对应拟合的贝塞尔函数表达式为:
(6)
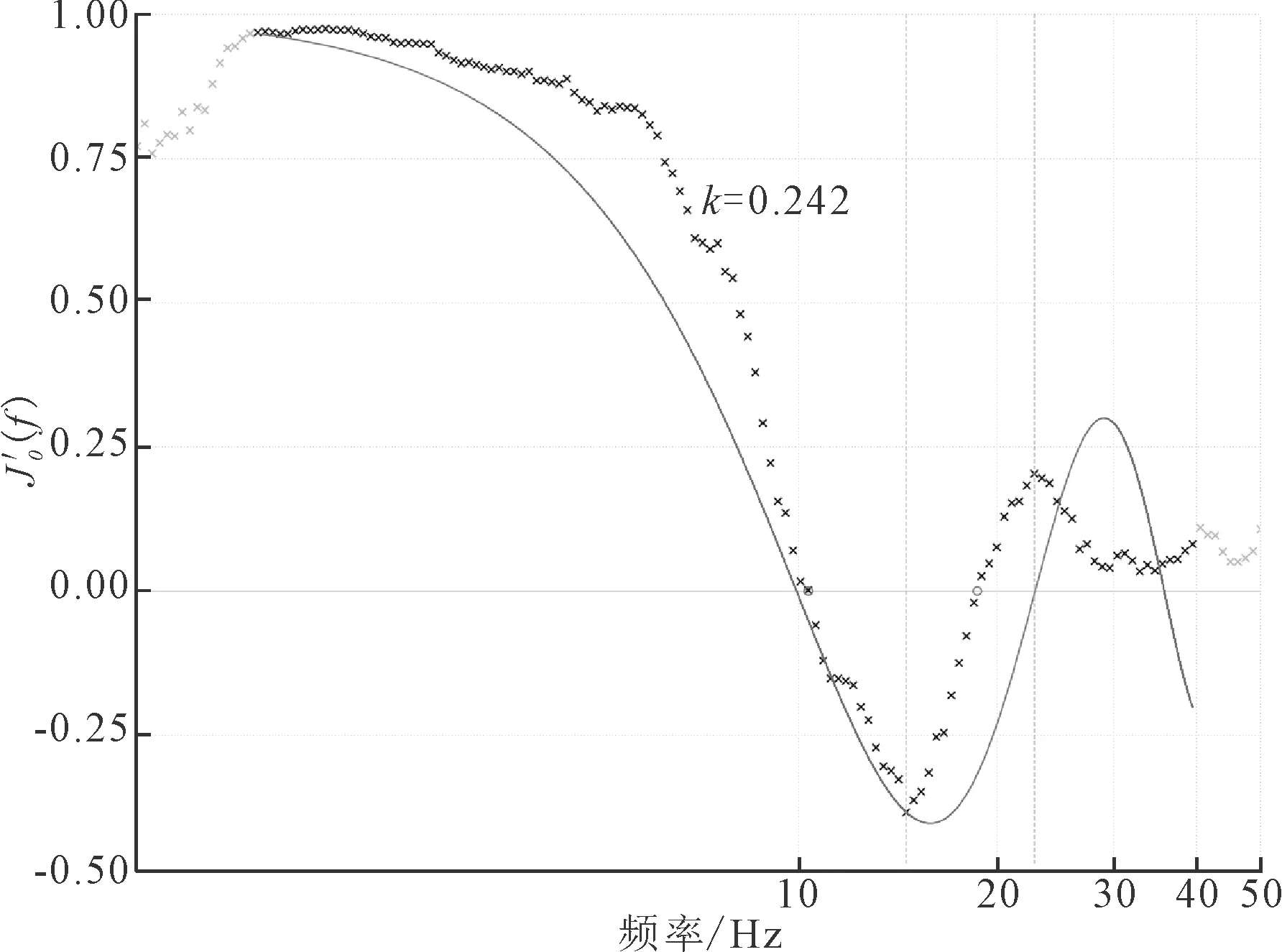
图1 汉克尔变换拟合贝塞尔曲线
通过相干系数的极点划分单调区间段,容易受到局部特殊点的影响,造成分段错误。而汉克尔变换利用了所有频点进行积分运算,不受特殊点的影响,其结果更具有鲁棒性。
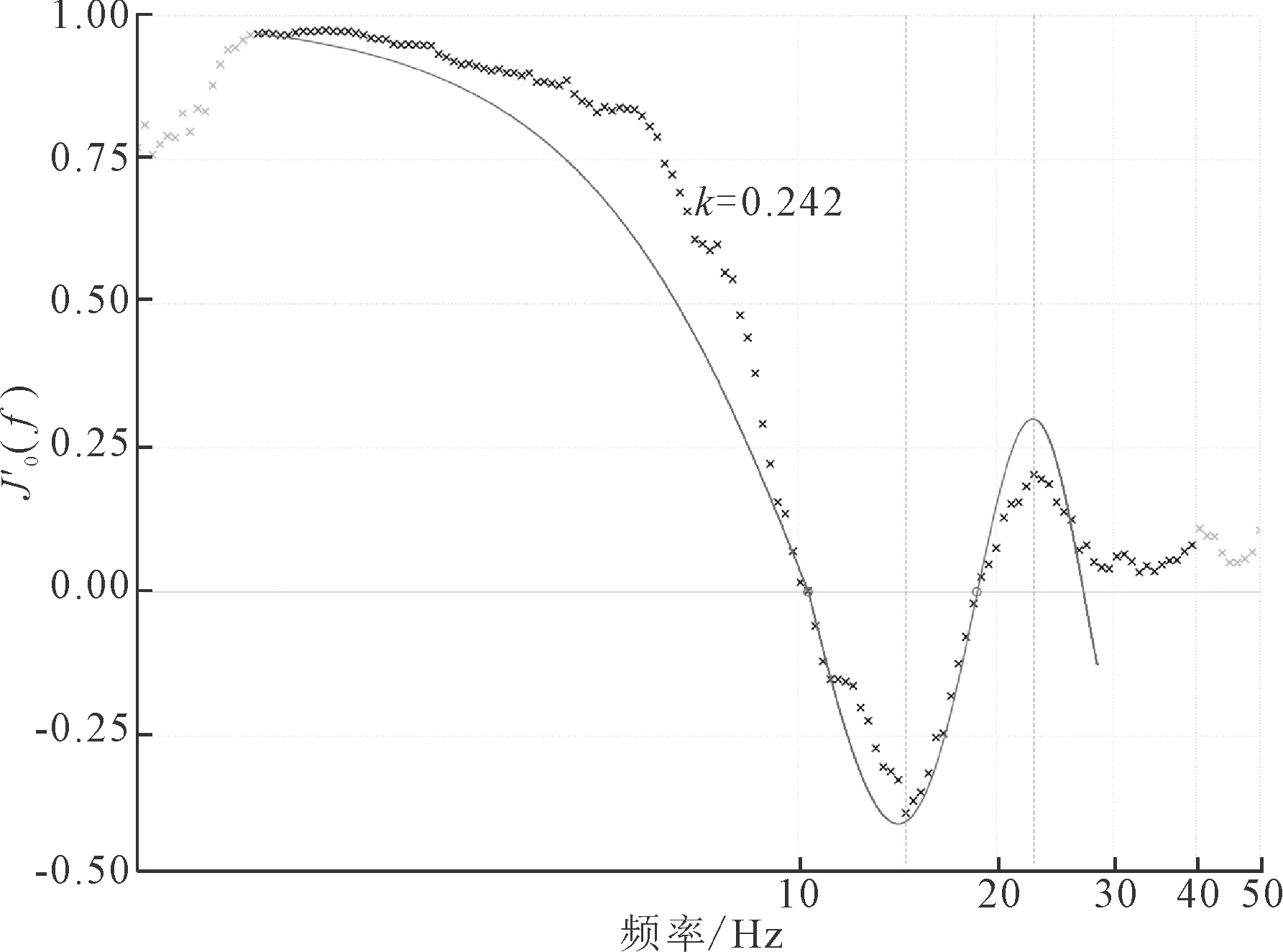
图2 多段汉克尔变换拟合贝塞尔曲线
将不同区间段的相干系数分别与图3所示的标准零阶第一类贝塞尔函数对应段拟合,求解相速度。
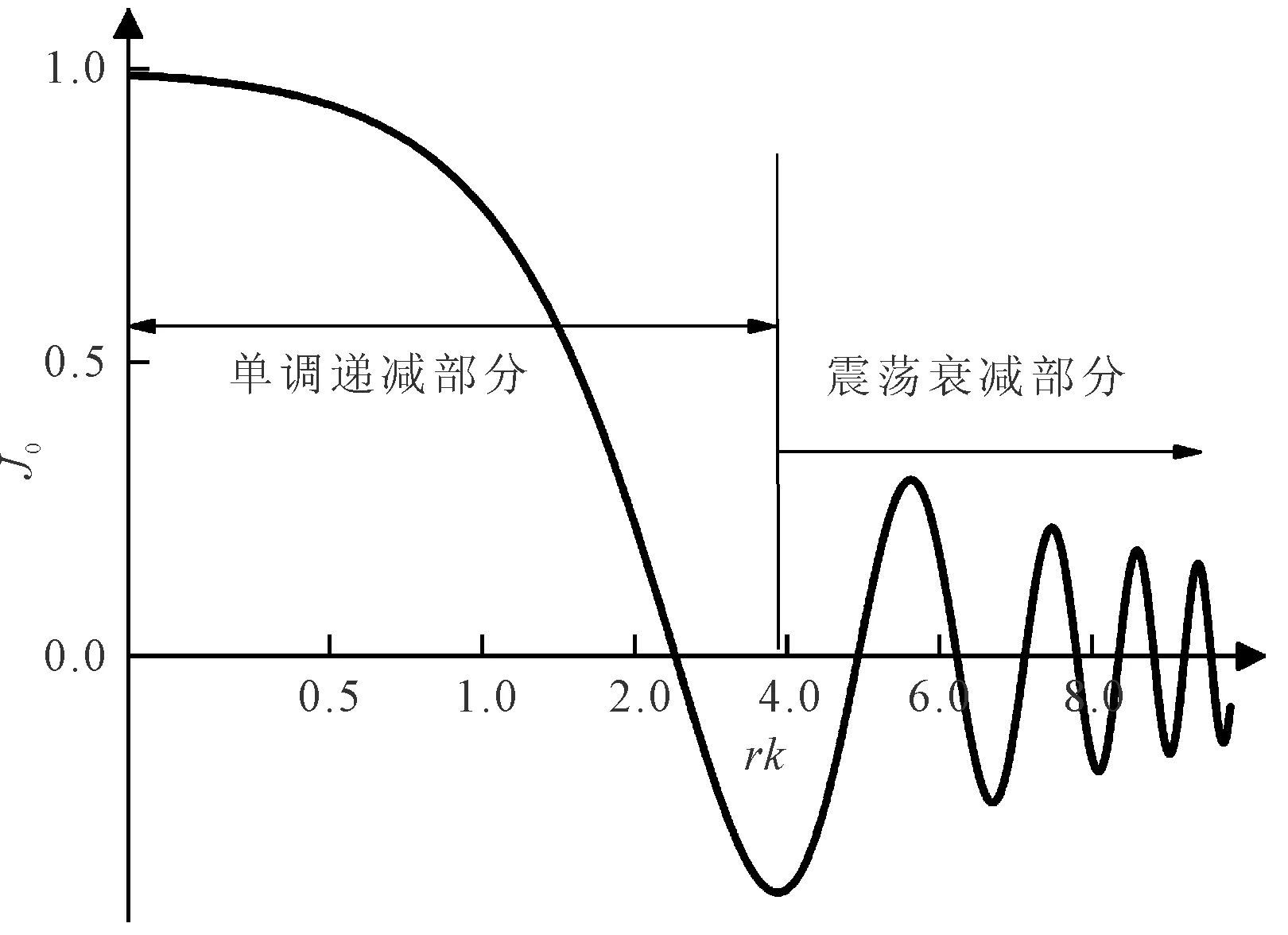
图3 标准零阶第一类贝塞尔函数
2 微动数据采集及其处理
2.1 微动数据采集
图4为本次实验用到的13个检波器,由实验室自主研发。检波器收集3个分量的微动信号,存储在SD(secure digital)卡中,采集完成后通过WiFi将数据导出。

图4 微动智能勘探仪检波器
本次实验设计了直线型阵列,一共有13个测点,相邻测点间隔5 m,布置在马路旁。微动观测阵列布置如图5所示。

图5 观测阵列
实验选择在工作日的下午两点至四点进行,记录采集时长60 min,采样频率250 Hz,测得的13个检波器垂直分量原始波形如图6所示。
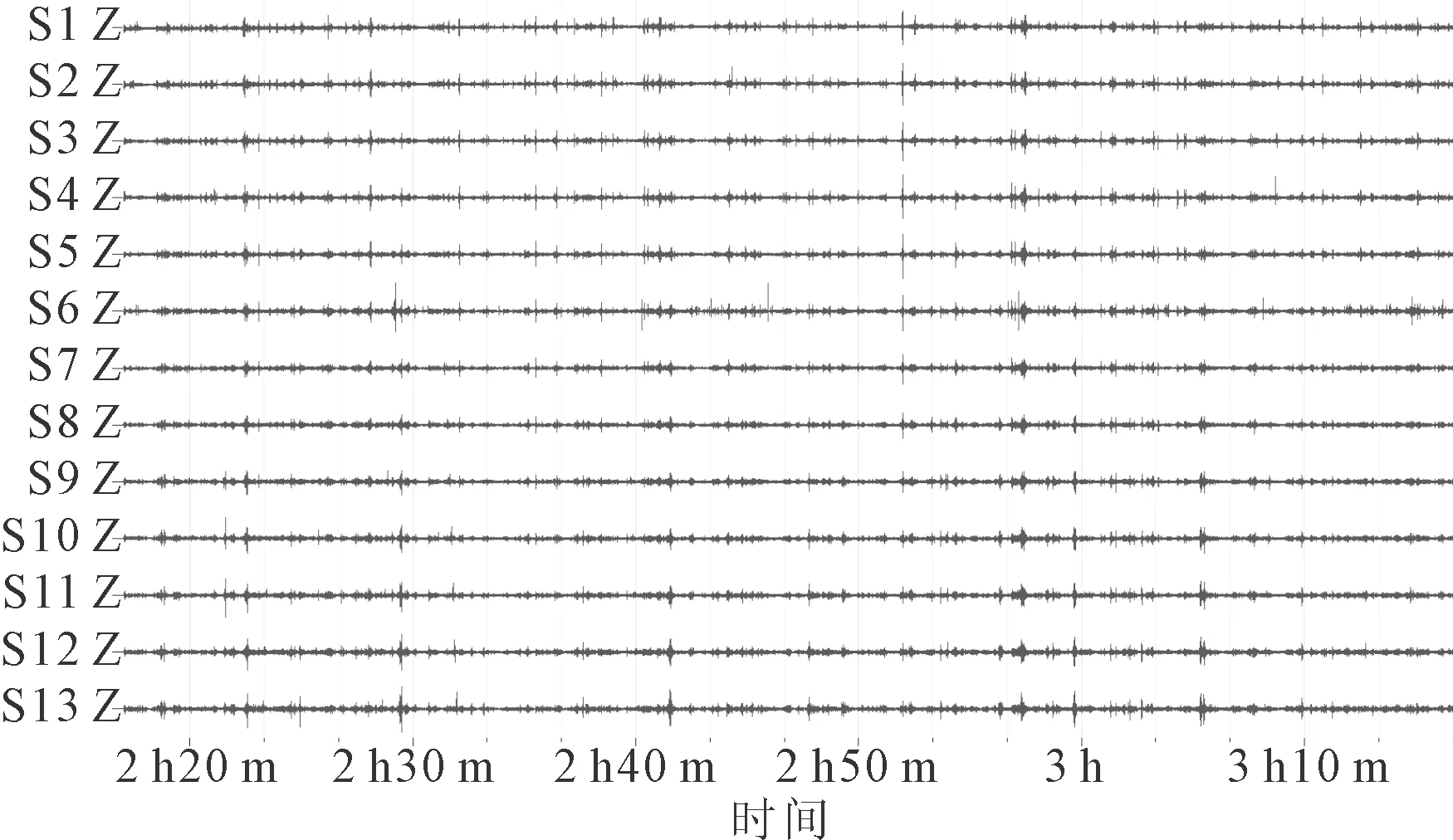
图6 微动波形
2.2 相干系数计算
通过式(2)计算10 m间距两两检波器微动数据之间的相干系数,结果如图7所示。从曲线形态上分析,11组数据具有良好的一致性,特别是在1.5~22 Hz区间段,曲线形状接近,并且近似满足贝塞尔函数的形状,包含单调递减部分和震荡衰减部分。从数据有效性的角度分析,1.5 Hz以下和40 Hz以上的部分相干系数震荡幅度大,数据的可靠性较低。后续进行相干系数分段,贝塞尔函数拟合时,需要把这些不可靠的数据剔除。计算选取的有效数据段是2~40 Hz。
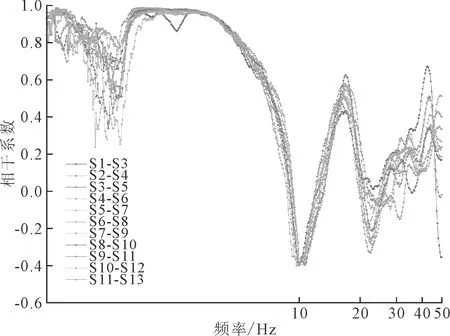
图7 相干系数
2.3 相干系数分段
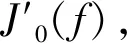

图8 S1-S3拟合贝塞尔曲线
对10 m距离的11道相干系数进行汉克尔变换,求得各段的最优解如表1所示。

表1 汉克尔变化的最优解
利用式(6)拟合相干系数曲线,得到拟合的贝塞尔函数,基于拟合的贝塞尔函数确定的分段点信息如表2所示。

表2 基于多段汉克尔变换的分段区间
2.4 频散曲线提取
利用表2所示信息,把相干系数分成4段,使用分段后的数据分别与标准贝塞尔函数对应单调段拟合,求解相速度,结果如图9所示。

图9 多段汉克尔变换后的相速度频散曲线
图10为传统的地震干涉算法处理得到的相速度频散曲线。从图10可知,使用汉克尔变换分段拟合的方法,将频率范围从8 Hz左右扩展到32 Hz左右,并且扩展频散点的相速度在200 m/s范围以内。
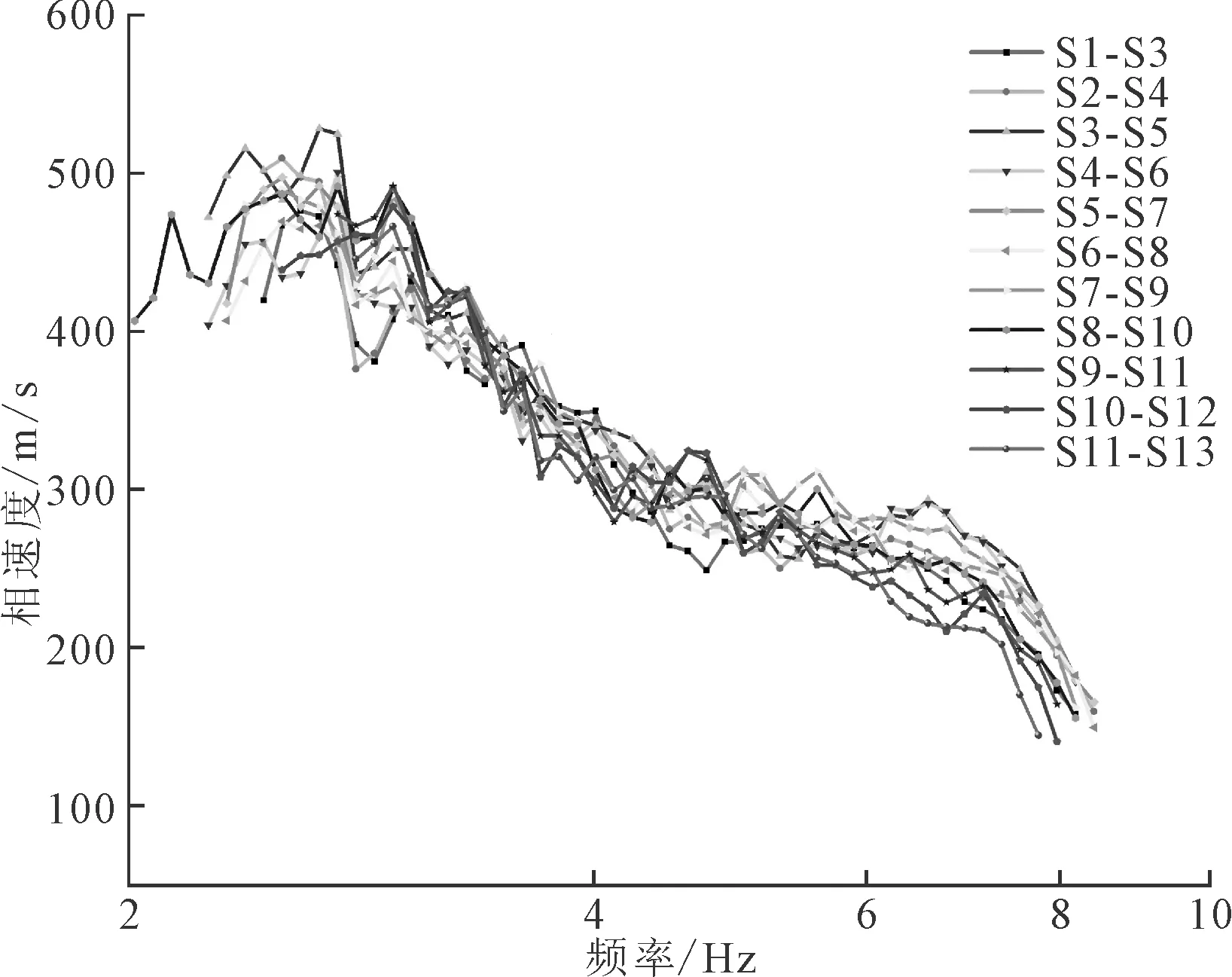
图10 单调递减段的相速度频散曲线
根据半波长深度定理,可以简单估算面波穿透深度。使用汉克尔变换分段拟合计算的频散曲线的半波长深度曲线如图11所示,探测深度范围约为2.5~110 m。传统方法的半波长深度曲线如图12所示,高频信息缺失,探测的深度范围约为10~110 m。

图11 多段汉克尔变换后的半波长深度曲线
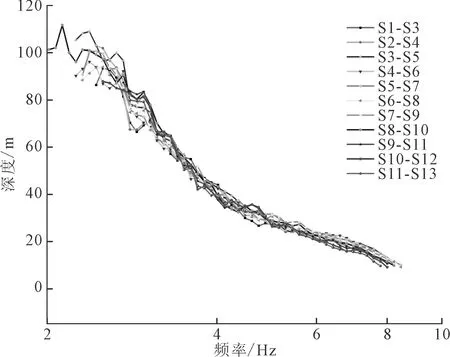
图12 单调递减段的半波长深度曲线
传统方法的半波长曲线揭示的最小探测深度约为10 m,本文的基于汉克尔变换分段拟合方法得到的半波长曲线揭示的最小探测深度约为2.5 m。本文提出的方法探测的最浅深度更小,对应的地下浅层面波结构细节更多。
3 勘探结果分析
使用相速度频散曲线,经插值运算绘制面波相速度等值线图,可以作为地质解释的基本依据。图13为使用单调递减段拟合求得的相速度绘制的面波相速度等值线图。图14为基于汉克尔变换分段拟合求得的相速度绘制的面波相速度等值线图。图中颜色代表面波相速度,速度大小如色标所示。
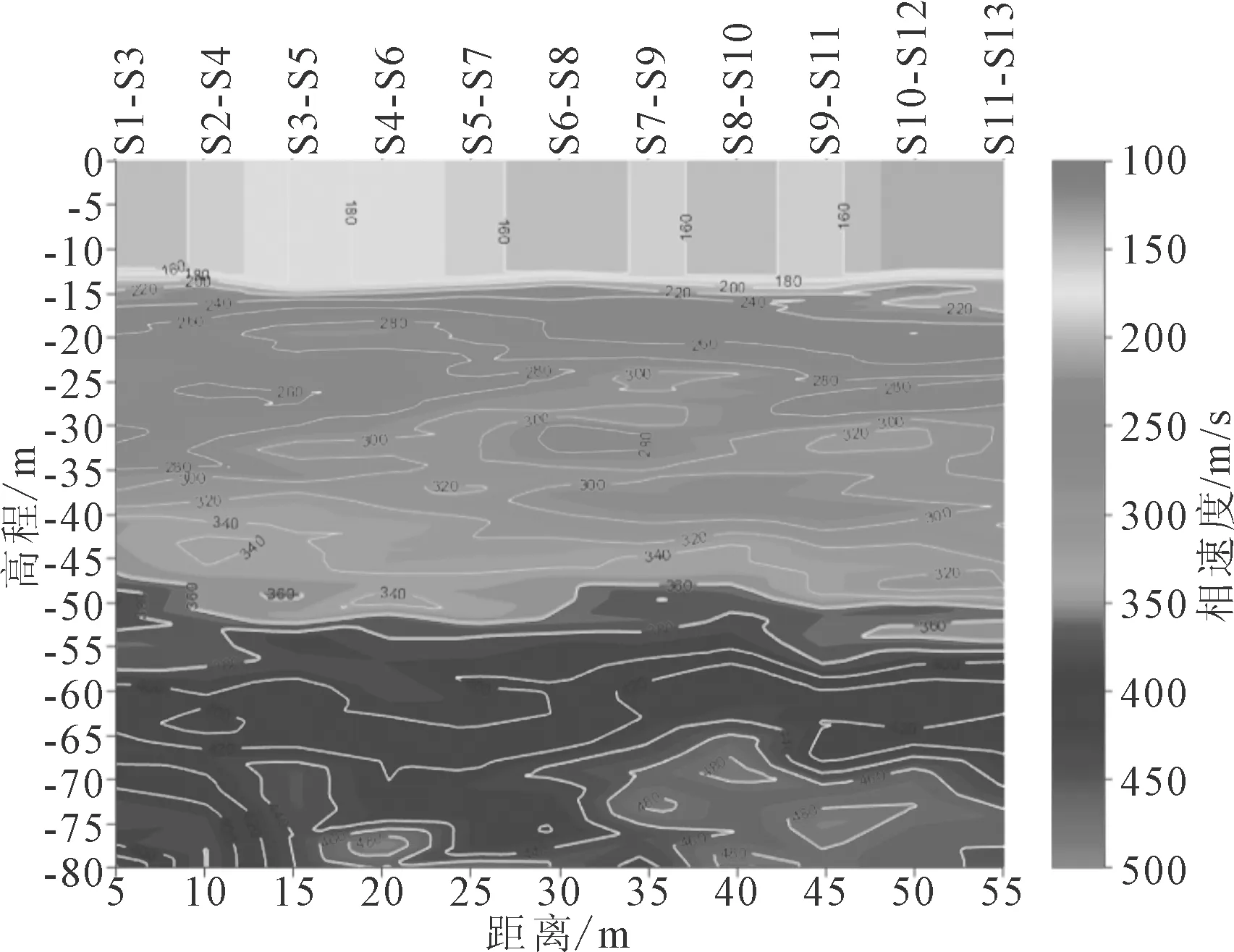
图13 单调递减段拟合的剖面图
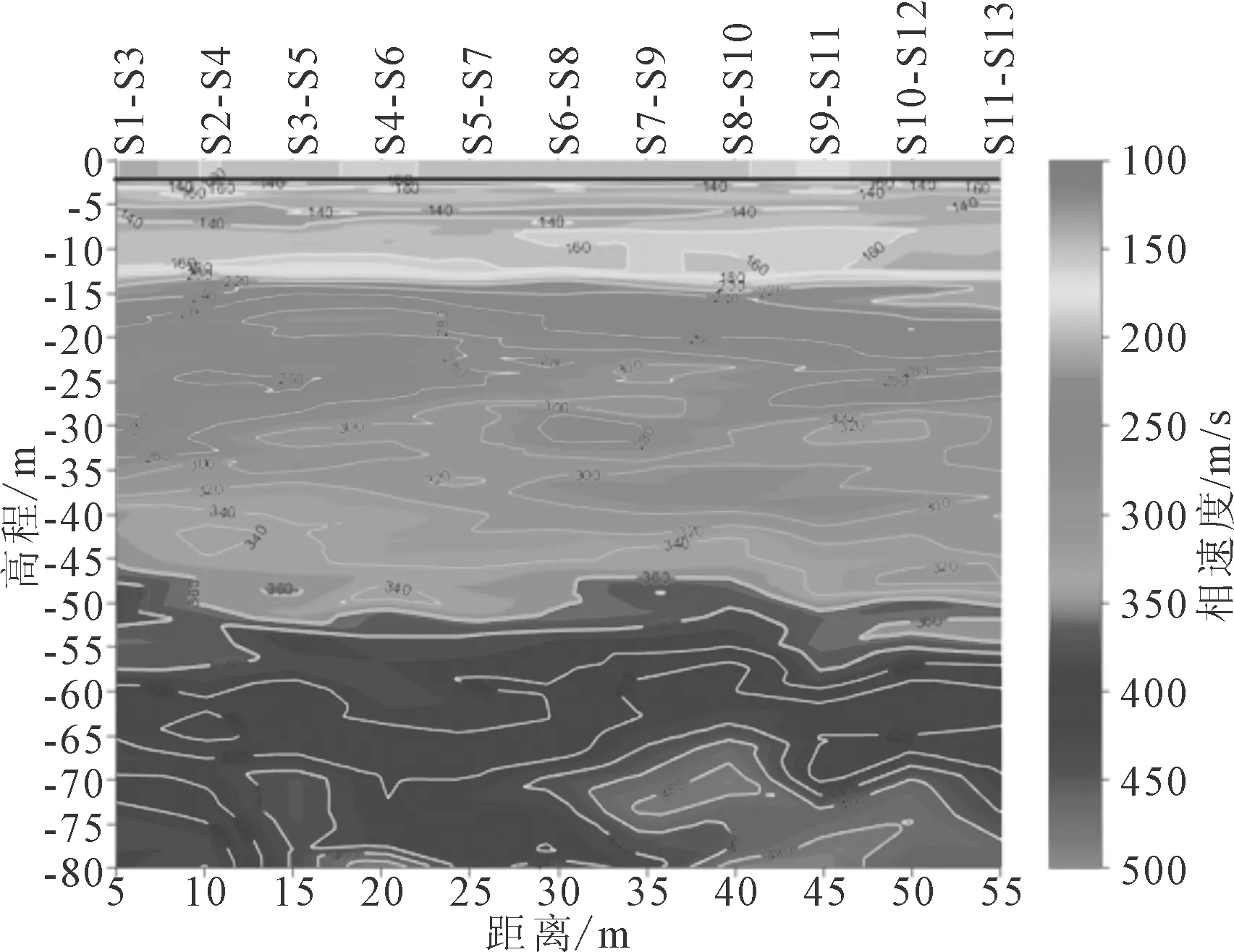
图14 基于汉克尔变换拟合的剖面图
使用传统的单调递减段拟合的地震干涉法和基于多段汉克尔变换的分段拟合的地震干涉法,得到的面波相速度等值线图,在大于12 m深度的区域基本一致,但是传统方法在浅部的探测盲区深度约为12 m,改进的方法探测盲区约为2.5 m。
4 结论
笔者针对SI算法求取面波相速度高频数据缺失,探测盲区大的问题,提出了基于汉克尔变换的分段拟合方法。将相干系数根据零点初步分段,然后在每一段使用汉克尔变换,确定拟合的分段区间,最后与零阶贝塞尔函数拟合求解相速度。实验表明,本方法可以有效扩展高频的频散数据,减小台阵的探测盲区深度,探测能力可以达到台站距离的1/4。
