直线导轨表面误差建模及多尺度曲线拟合方法研究

冯石冲,凌 鹤

(武汉理工大学 机电工程学院,湖北 武汉 430070)

导轨在机床上起到导向和承重功能,它具有高刚度、低摩擦和低磨损的特点。导轨的精度显著影响机床的加工精度和性能,因此,提高导轨的精度对于提高机床的加工精度和性能具有十分重要的意义[1]。目前导轨的加工工艺流程一般为:坯料→轧制→热处理→矫直→钻孔→再矫直→磨削。其中,矫直和磨削是提升导轨精度的两个重要工艺。矫直,是将金属条材由弯变直的一种加工工艺。磨削,往往作为矫直加工的后续工艺,它是使用硬磨粒颗粒去除工件材料的加工工艺。机床导轨作为一种精密导向部件,需要有良好的几何精度和表面性能。矫直和磨削是导轨加工过程中的两道连续加工工艺,这两道工艺之间的相互作用会对导轨的性能产生一定的影响。因此,综合考虑两种加工工艺对导轨精度的影响是极为重要的。在制定导轨的加工工艺之前,首先需要对导轨的表面进行研究。

工件的表面具有随机性和不规则性,为了准确地研究机械加工工艺对工件表面形貌的影响,首先需要建立工件表面形貌的几何模型。一些学者在研究导轨的矫直工艺时将导轨表面误差看作简单挠曲线,例如圆弧和二次曲线[2]。此外,一些学者在研究导轨上工作台的运动误差时将导轨表面误差看作周期函数,例如三角函数[3-10]。还有一些学者将上述两种曲线特性结合起来,例如Tang等将导轨表面误差看作二次曲线和三角函数的叠加[11]。然而,上述学者提出的导轨模型与实际的导轨表面依然存在较大误差。一般而言,工件的表面误差分为3种类型:形状误差、波纹度误差和粗糙度误差。形状误差指的是宏观上的误差,一般使用多项式函数表示;波纹度误差指的是中观上有周期性波动的误差,一般使用三角函数表示;粗糙度误差则属于微观上的误差,一般使用分形函数表示。这3种类型的误差并不是单独存在的,实际的加工表面往往是这3种误差的综合。由于不同类型的误差有不同的形成原因,同时也对工件的表面性能有不同影响。因此,为了正确区分这些误差,从而更好地制定工件的加工工艺,将这3类误差从工件表面分离出来就极为重要。一些学者建立了各种各样的方法对工件的表面误差进行分离,例如傅里叶变换、高斯滤波、小波变换和离散模态分解。然而这些方法有着一定的局限性。当研究对象有具体的应用场景时,往往非常耗时,且分离出来的结果不能满足特定的力学背景,难以将分离出来的误差用于实际加工。

基于上述原因,笔者从导轨的误差来源类型出发,将导轨的表面形貌误差看作多项式、三角函数和分形函数的叠加,建立了直线导轨的表面轮廓误差模型。为了准确、快速地辨识这几种类型的误差,提出了多尺度曲线拟合方法。然后,基于多尺度曲线拟合方法,对直线导轨的表面轮廓误差进行分解。最后,实验验证了误差模型和多尺度曲线拟合方法的有效性。

1 直线导轨表面轮廓误差模型

机床工作台的直线度误差主要来源于直线导轨的表面形貌误差,导轨在与机床导轨并行的水平面xoy平面内的表面形貌误差使工作台在运动过程中产生了直线度误差δz(x)。因此,笔者针对直线导轨在xoy平面内的表面形貌进行研究。将表面形貌误差分解为一系列在y=yj(j=0,1,…,t)平面内的表面轮廓误差的集合,t为平面的个数换句话说,把三维的表面形貌误差转化为许多个二维的表面轮廓误差。于是,表面形貌误差能够使用表面轮廓误差点集S(yj)表示。为了研究表面轮廓误差的几何特征,以任意y=yj(j=0,1,…,t)平面为分析对象。

2 多尺度曲线拟合方法

2.1 形状误差模型

直线导轨在生产过程中,要经历轧制、热处理,打孔等制造工艺,不可避免地产生弯曲和扭曲变形。为了研究方便,仅考虑单弯曲的直线导轨表面轮廓的形状误差。

根据魏尔斯特拉斯第一定理,任意的连续函数可以使用多项式来逼近,如图1所示。因此,单弯曲的直线导轨在y=yj(j=0,1,…,t)平面内的表面轮廓的形状误差可以使用多项式P(x)j来逼近。即

图1 单弯曲的直线导轨表面轮廓的形状误差

P(x)j=p0,j+p1,jx+…+pn,jxn

(1)

式中,多项式系数p0,j,p1,j,p2,j,…,pn,j为任意实数。

2.2 波纹度误差模型

直线导轨的表面轮廓并不是一条简单的、光滑的多项式曲线,它的表面存在着波纹度。如图2所示,周期曲线表示直线导轨的波纹度。根据Fourier级数的知识,直线导轨的波纹度可以使用三角多项式来逼近。因此,直线导轨在y=yj(j=0,1,…,t)表面轮廓的波纹度误差可表示为:

图2 直线导轨表面轮廓的波纹度误差

(2)

式中:系数ak,j,bk,j为任意实数。

2.3 粗糙度误差模型

除了形状误差和波纹度误差,导轨表面还存在粗糙度误差。表面轮廓的粗糙度误差一般使用常见的分形函数W-M函数来表示,因此直线导轨在y=yj(j=0,1,…,t)平面内的表面轮廓的粗糙度误差可以表示为R(x)。

2.4 多尺度曲线拟合

为了更加准确地描述直线导轨的表面轮廓误差,将简单多项式P(x)j、三角多项式f(x)j和分形函数R(x)j结合起来,同时考虑到粗糙度误差R(x)的表达式非常复杂,可以将表面粗糙度R(x)看作曲线拟合过程的拟合误差。因此,导轨在y=yj(j=0,1,…,t)平面内的表面轮廓可以使用式(3)来拟合:

z(x)j=p0,j+p1,jx+p2,jx2+

(3)

拟合曲线的图像如图3所示。将式(3)写成矩阵形式:

图3 一个平面内的表面轮廓误差曲线

Z=Mp+fXp+f

(4)

式中:矩阵X为式(3)中x,x2,sinx,cosx,sin2x,cos2x组成的基矩阵;矩阵M为式(3)中p0,j,p1,j,p2,j,a1,j,b1,j,a2,j,b2,j的系数矩阵。

式(4)的解为:

(5)

式中,X-1代表矩阵X的广义逆矩阵。

从式(5)可知,通过求解线性方程组将形状误差、波纹度误差和粗糙度误差从整个导轨的表面轮廓中分离出来。这为后续的矫直和磨削加工工艺提供了重要信息。

3 直线导轨表面轮廓误差分析实例

3.1 实验材料与实验仪器

本实验选用三坐标测量机来测量3根直线导轨的表面形貌误差,其型号为:Daisy564。实验材料为同一批加工的3根直线导轨,尺寸均为:400×20×20 mm,分别将其编号为:LG1,LG2,LG3。

三坐标测量机在每根导轨上测量3个平行表面的轮廓,每个轮廓上选取41个测量点,每个测量点的间距为10 mm。

3.2 实验结果与数据分析

从实验结果可知,同一根导轨上的3条轮廓曲线非常接近。因此将同一根导轨上的3条轮廓曲线取平均值,然后使用所提出的多尺度曲线拟合方法对导轨进行曲线拟合。

导轨LG1、LG2、LG3表面轮廓的曲线拟合结果分别如图4～图6所示。可以看出,使用多尺度曲线拟合方法对导轨表面轮廓进行曲线拟合的效果很好。

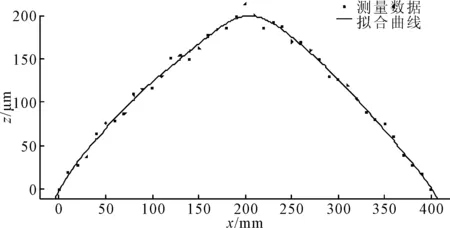
图4 导轨LG1的测量数据及拟合曲线

图5 导轨LG2的测量数据及拟合曲线

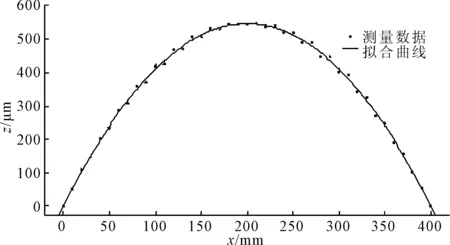
图6 导轨LG3的测量数据及拟合曲线

为了更准确地说明拟合效果,将多尺度曲线拟合方法与二次多项式的曲线拟合进行对比。结果如表1所示。

表1 两种曲线拟合的对比

导轨LG1和导轨LG2使用多尺度曲线拟合方法的拟合效果要优于二次多项式拟合,均方误差分别减小了46%和41%。导轨LG3使用两种拟合方法的区别不大,均方误差几乎不变。

4 结论

笔者选取了3根相同工艺的导轨作为实验样件,分别测量每根导轨上的3个平行面的表面轮廓误差。对比每根导轨上的3条轮廓曲线,发现3条轮廓曲线非常接近。这表明:导轨的轮廓误差主要沿着导轨的长度方向变化,在宽度方向上几乎不变。

笔者建立了直线导轨的表面轮廓模型,然后使用多尺度曲线拟合方法对3根导轨的测量数据进行拟合,同时对比传统的二次多项式的曲线拟合方法。可以发现,多尺度曲线拟合方法的拟合效果要优于传统的二次多项式拟合,均方误差明显减小,最大可以减小46%。值得注意的是,随着导轨的形状误差越来越小,两种拟合方法的差距越明显。因此,多尺度曲线拟合方法更适用于直线导轨表面误差的分解。