五模块铰接有轨电车调簧算法研究
2023-09-20刘伟渭陈靖雨高明杰
刘伟渭,陈靖雨,高明杰,王 勇,江 哲,刘 命
(西南交通大学 机械工程学院,成都 610031)
城市轨道车辆的轴重和轮重控制是设计过程中的关键内容,车轮载荷分布以及轴重偏差大小会直接影响车辆的附着力[1-2],对车辆黏着制动力和牵引力的发挥以及车辆整体的动力学性能具有重要影响[3-5],所以需要保证车辆的轮轴重偏差率在行业规定范围内,以便从车辆静态性能控制的角度去改善和确保车辆的动态运行性能。
根据IEC-61133—2006《车辆组装和运行前的整车试验规范》[6]、GB/T-32383—2020《城市轨道交通直线电机车辆通用技术条件》[7]要求,轮轴重偏差率需满足:任一侧各车轮轮重与两侧轮重平均值之差不得大于±4%,任一车轴上的任一轮重与该轴平均轮重之差不得大于±4%;各车任一动轴的轴重不得超过其动轴平均重量的±2%,各车任一拖轴的轴重不得超过其拖轴平均重量的±1%。
列车从设计到制造,再到新车装配生产下线进行出产试验,时常会出现车辆轮轴重偏差超限的情况,这时需进行轮轴重偏差调整。目前处理措施一般是进行加垫调簧,即在车辆的一系簧或二系簧支撑处加入垫片以改变和重新分配车辆轮轴重来满足规范要求[8-11]。目前轨道车辆的加垫调簧基本靠作业人员经验对加垫位置、加垫量进行确定,对于一二系悬挂支撑位置较少的动车或地铁车辆调簧相对较为容易,若遇到车间耦合复杂的铰接式转向架、铰接式多模块浮车等车型,仅靠人员经验基本很难调平。
五模块浮车是有轨电车中车间铰接最复杂、一二系支撑位置最多的一种车型,由于二四位车体的悬浮使得车体纵向重心易产生较大偏差,而使得列车的轮轴重偏差十分容易超限[12-13]。另外该车型在加垫时车体、构架、轮对需完全吊装、拆解,每次尝试一种加垫方案将耗费约一天时间,所以亟需一种有效的调簧算法支撑以提升作业效率和调簧精度。
1 车辆结构
五模块有轨电车是一款100% 低地板浮车,如图1所示,车辆配置有悬浮车体,悬浮车体下方没有转向架,通过车体两端的铰接装置连挂在相邻车体上。该车型以其低碳环保、成本低、运量大、乘坐便捷、外形美观等特点,在国内市场迅速兴起[14-15]。

图1 五模块有轨电车型有轨电车Fig.1 Streetcar of five-module floating
车辆编组形式为“Mc1+F1+Tp+F2+Mc2 ”,如图2所示,其中Mc1、Tp、Mc2 车体配置转向架,Mc1和Mc2为动车;Tp车为拖车;F1、F2悬浮于前后车辆,通过车间铰接与两侧车体相连。

图2 整车编组结构示意图Fig.2 Schematic diagram of vehicle grouping structure
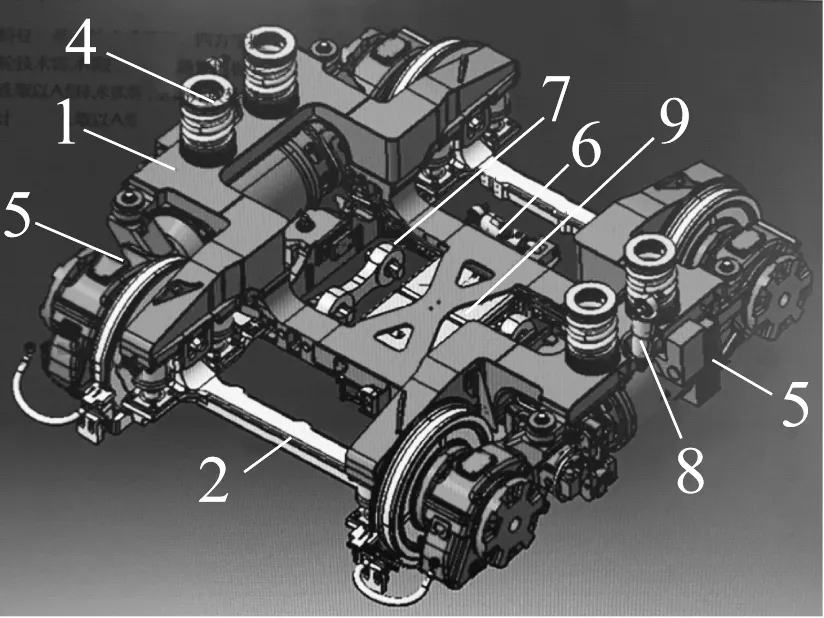
动车转向架和拖车转向架结构如图3所示,转向架由两个独立轮对组成,轴箱采用内置式一系悬挂弹簧,构架与车体间由8个刚簧连接。车辆每个模块之间通过铰接进行连接,该车型共使用三种类型的铰接,包括自由铰、弹性铰和固定铰。
(a)
固定铰总成由关节轴承、轴承座组成。通过螺栓安装在车体上。铰接本身实现车辆水平转动、侧滚及点头,具有垂向、纵向、横向方向的刚度,根据测量X向受力时的变形量得到其X向刚度值,如图4所示。

图4 下部固定铰Fig.4 Lower fixed hinge
上部弹性铰主要由2个固定组件和1个带轴承的拉杆组成,冲压件与拉杆体通过轴承连接在一起,主要允许车体模块的水平转动、侧滚,本身不能实现点头功能,但随车辆侧滚运动而产生点头,具有纵向、横向方向的刚度,如图5所示。
图5 上部弹性铰Fig.5 Upper elastic hinge
上部自由铰由两个钣金件和中间限位拉杆组成。允许车体模块间的水平转动、侧滚及点头,具有横向方向的刚度,如图6所示。车辆相关技术参数如表1所示。

表1 车辆参数表格Tab.1 Table of vehicle parameters

图6 上部自由铰Fig.6 Upper free hinge
2 力学模型
车辆的车体、构架等部件等效为具有质量的刚体,承载部件等效为刚度力元。一系弹簧和二系弹簧主要传递垂向力,因此等效为单个刚度力元,建立车辆等效模型如图7所示。
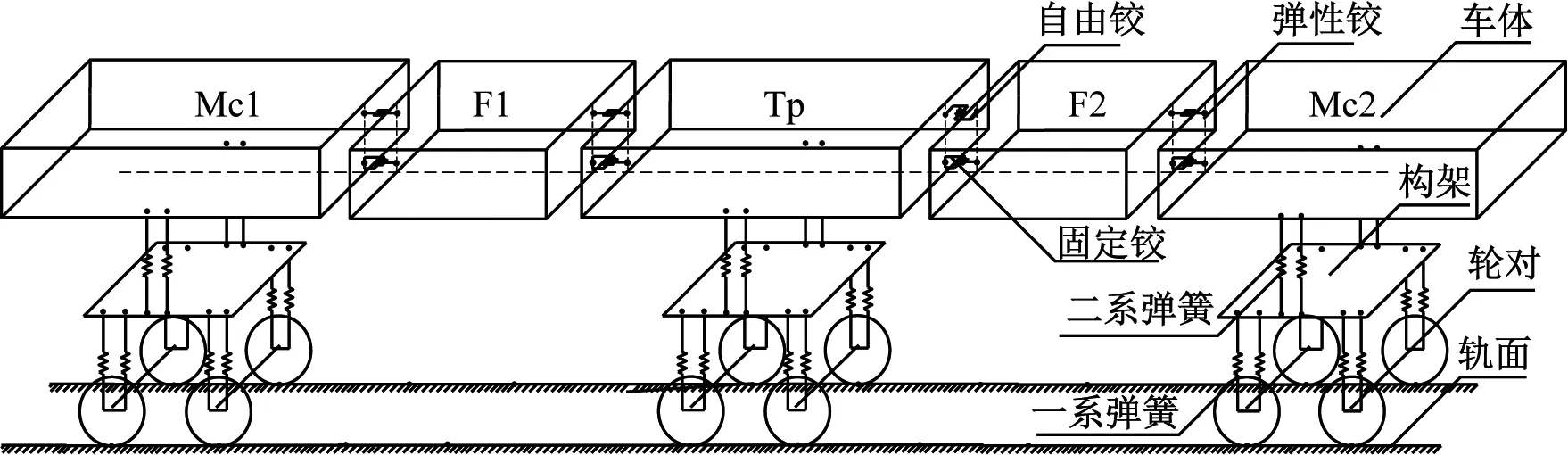
图7 车辆系统等效模型Fig.7 Vehicle system equivalent model
车辆的下铰接均为固定铰,而上铰接为了保证车辆具有良好的通过竖直曲线能力,在 Tp模块和F1模块之间采用开放铰进行连接,其余上铰位置采用弹性铰对车辆进行连接。固定铰和弹性铰的组合使用使得相连接的两个模块之间仅有相对摇头自由度,传递纵向、垂向和横向力。固定铰和自由铰的组合使用使得相连接的两个模块既有相对摇头自由度又有相对点头自由度而产生垂向和横向力,受力分析如图8所示。

图8 车辆系统力学模型Fig.8 Mechanical model of vehicle system
3 调簧模型
对于如图7的车辆系统等效模型,车体、构架具有浮沉、侧滚、点头3个自由度,轮对具有浮沉、侧滚2个自由度。车辆系统共36个自由度,其中车体共15个自由度,转向架共9个自由度,轮对共12个自由度。具体如表2所示。
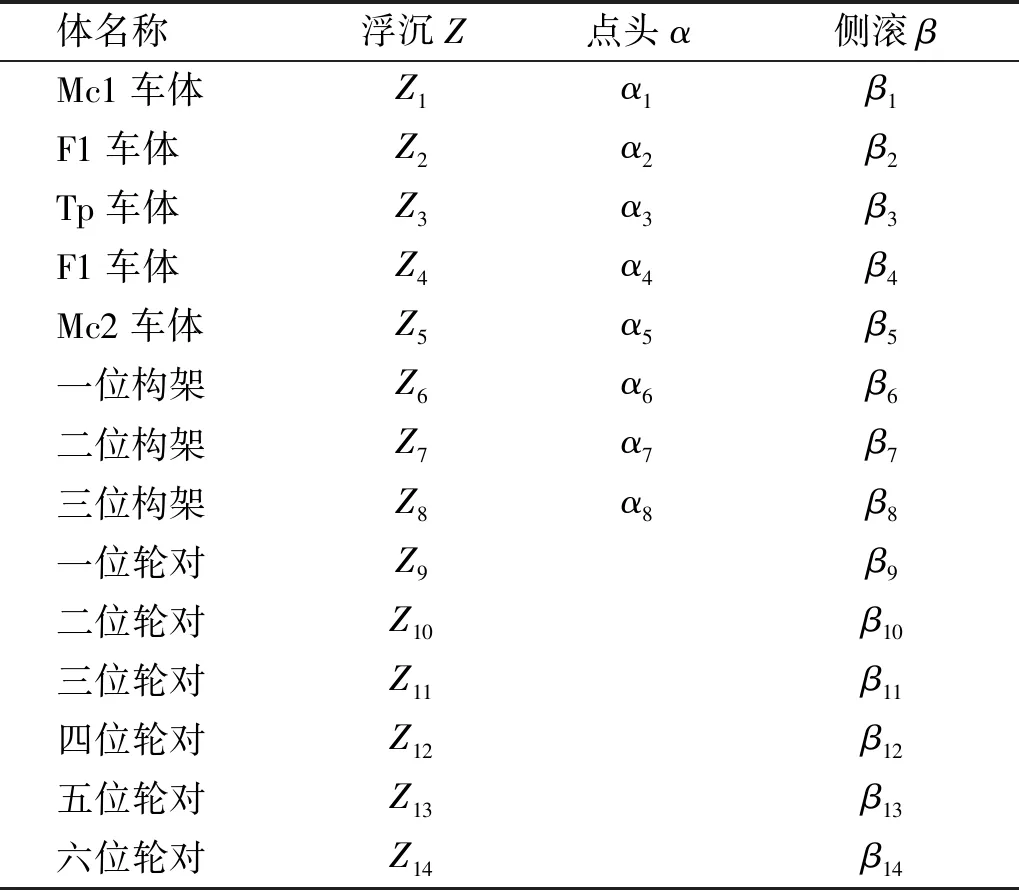
表2 系统自由度定义Tab.2 System freedom definition
对于如图7的车辆系统等效模型,定义如表3的各支撑簧刚度名称,共67个刚度系数,其中二系弹簧12个,一系弹簧24个,铰接刚度19个,轮轨接触刚度12个。

表3 系统刚度定义Tab.3 System stiffness definition
对于如图7的车辆系统等效模型,车辆结构中的弹簧横向跨距、纵向跨距等参数符号及数值如表4所示。

表4 车辆尺寸参数表Tab.4 Parameter table of vehicle size
对于如图7的车辆系统等效模型刚度系数矩阵为
k=diag(K1,K2,…,K66,K67)
(1)
系统的刚度矩阵K则为
K=TTkT
(2)
式中,T为刚度关联矩阵,T=[T1,T2],如表5所示。
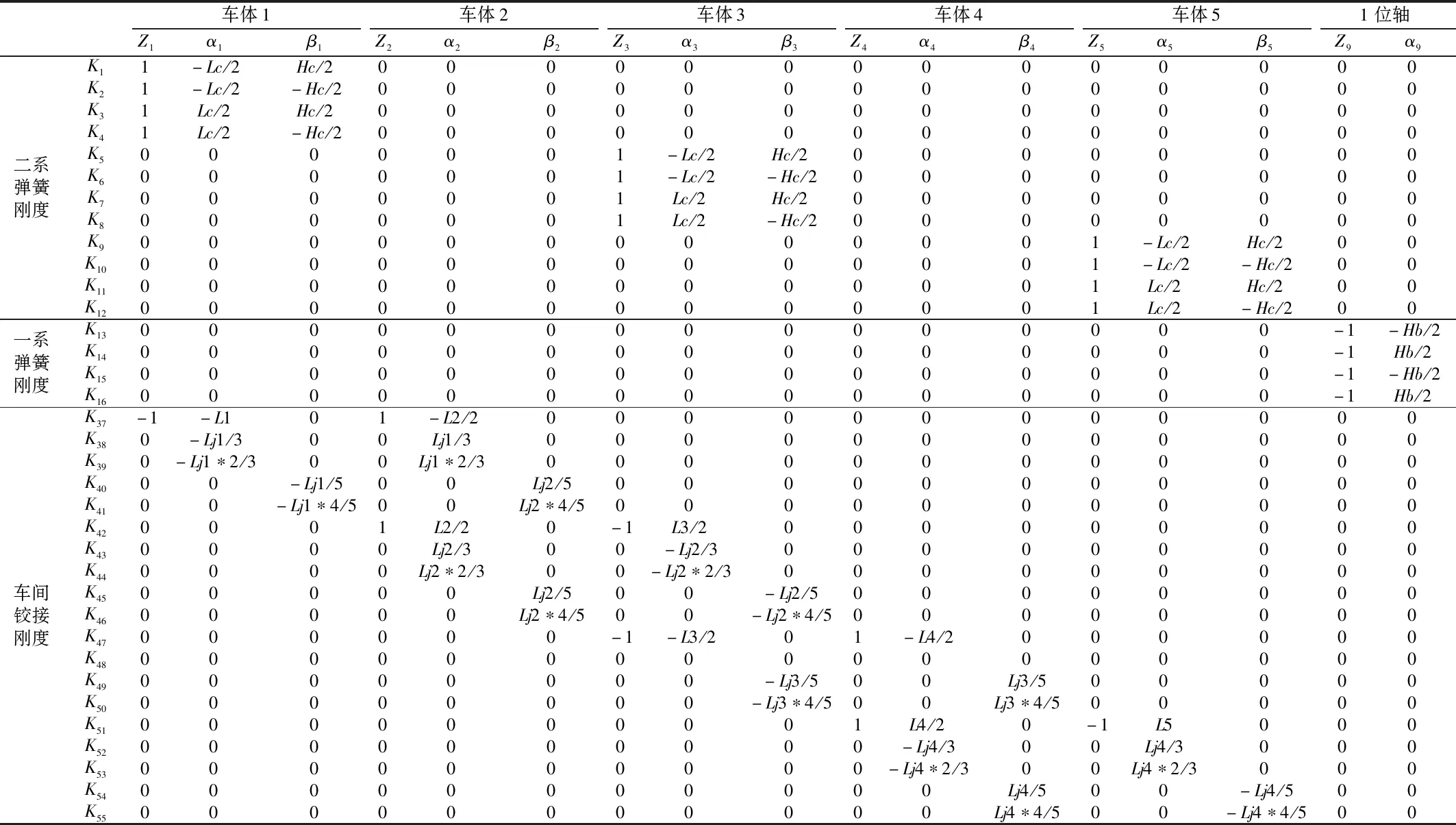
表5 刚度关联矩阵表T1Tab.5 Stiffness correlation T1 matrix table
假设加垫量为δi(i=1,…,67),则加垫向量为
δ=[δ1,δ2,δ3,δ4,δ5,δ6,…,δ66,δ67]T
(3)
式中:由于该车型车间铰不能加垫,所以加垫量δi只包括一系和二系位置,不包括车间铰接和轮轨接触刚度的δ37~δ67。
加垫向量δ与系统位移量x0关系为
δ=Tx0
(4)
加垫前后系统均为静态,系统无额外附加力,则弹簧加垫的系统方程为
TTkTx+TTkTx0=0
(5)
将式(4)代入式(5)整理得
TTk(Tx+δ)=0
(6)
即:
TTkTx=-TTkδ
(7)
Kx=F0
(8)
将式(8)系统平衡方程式代入式(7)可得调簧加垫后引起的外力矢量为
F0=-TTkδ
(9)
由式(8)可知调簧加垫后引起的系统位移为
x=K-1F0
(10)
所以调簧加垫后引起的弹簧载荷变化为
Fs=k(Tx+δ)
(11)
将式(11)得到的弹簧载荷变化量Fs中轮轨接触项数值,即Fs56,…,Fs67项与加垫调簧前初始轮重相加,即可得加垫调簧后各轮重和轴重,进一步可求得各轮重偏差和轴重偏差。
4 调簧分析
对于式(1)~式(11)的调簧方案较难有解析解,所以可通过确定一种指标参数,然后利用寻优逼近的方式求解。调簧的目的是让车辆称重时各偏差参数达标并尽可能小,所以该指标可基于IEC-61133—2006《车辆组装和运行前的整车试验规范》中的轮轴重偏差率要求来确定。在该规范中包括轮重偏差、动轴偏差、拖轴偏差三个单指标,各偏差百分比均不同,为能让各参数均达标,可将轮重偏差率、动轴重偏差率、拖轴重偏差率综合考虑,把所有超限时的偏差率百分比增补至4%,这样当指标值ζ算法≤4%时便能满足规范要求,如式(12)所示。另外,弹簧垫片最小厚度为1 mm,所以加垫方案中的加垫量需取整,且最大加垫量按规范要求不能超过5 mm。

ζ算法=Max(∂轮重,∂动轴重,∂拖轴重)
(12)
在计算调簧加垫方案时,采用成熟而通用的模拟退火算法和遗传算法对调簧模型指标值ζ算法进行寻优求解[16-22]。
列车下线和加垫后的轮轴重及偏差测量如图9所示的试验台进行。实测轮轴重分布如表6所示,其中:1、2、5、6位轴重超限,3位轴轮重超限,此时算法指标值为5.52%,即动轴最大偏差3.52%加补齐的2%。

表6 列车下线实测轮轴重和偏差值Tab.6 Measured wheel axle weight and deviation value

(a) 称重台
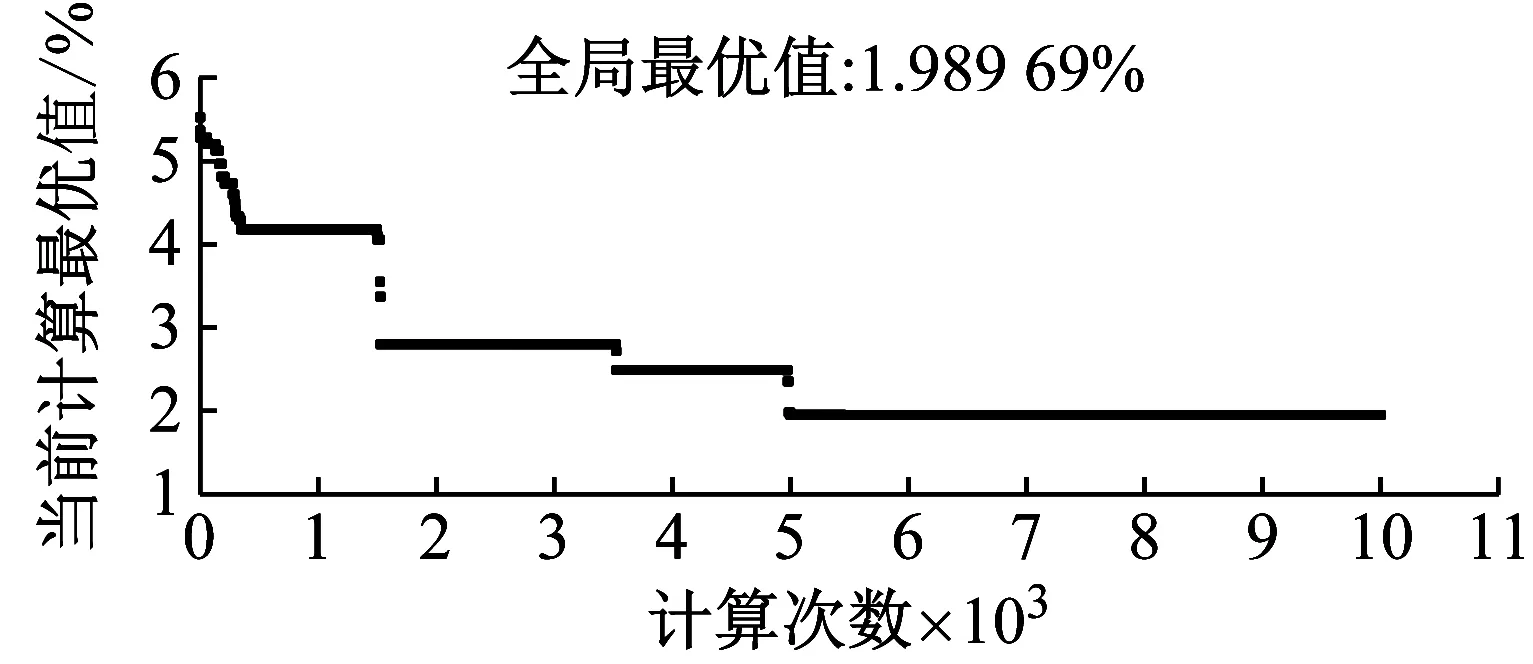
遗传算法迭代运算了10 000次,在5 000次左右达到理想值,通过反复25次的退火-升温循环,计算过程如图10所示,求得加垫量和加垫位置方案如表7,算法指标值ζ算法从5.52%降至1.99%。

表7 加垫方案(模拟退火)Tab.7 Padding scheme (simulated annealing)
(a)
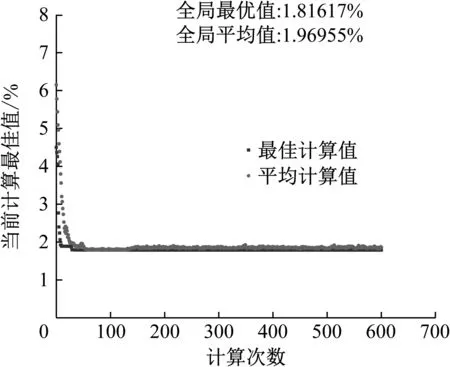
图11 遗传算法计算过程Fig.11 Calculated process of genetic algorithm
把表7的加垫方案进行调簧作业,加垫后的车辆轮轴重分布如表8和图12所示。可以看出,加垫后的轮轴重分布较为理想,各个车轮的轮轴重偏差均有不同程度降低,并满足试验规范要求。

表8 加垫后轮轴重及偏差试验结果(模拟退火)Tab.8 Axle load and deviation test results (simulated annealing)

(a)
遗传算法种群进化了600代,通过个体交叉遗传变异,在40代左右达到理想值如图11所示,求得加垫量和加垫位置方案如表9所示,算法指标ζ算法从5.52%降至1.82%。

表9 加垫方案(遗传算法)Tab.9 Padding scheme (genetic algorithm)
把表9的加垫方案进行调簧作业,加垫后的车辆轮轴重分布如表10和图13所示。可以看出:加垫后的轮轴重分布较为理想,各个车轮的轮轴重偏差均有不同程度降低,并满足试验规范要求。
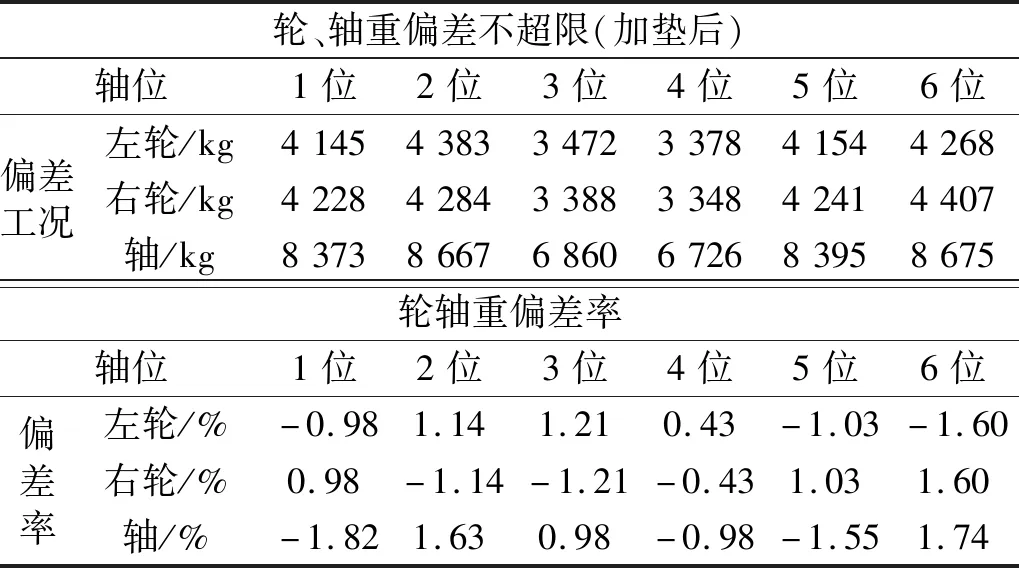
表10 加垫后轮轴重及偏差试验结果(遗传算法)Tab.10 Axle load and deviation test results (genetic algorithm)

(a)
5 结 论
本文研究结构特殊、受力复杂的五模块有轨电车调簧算法和试验验证。在建立五模块有轨电车等效车辆模型、力学模型基础上,给出了系统联合刚度矩阵、加垫调簧算法流程,把实测轮重作为调簧模型输入,利用模拟退火算法、遗传算法进行调簧方案的寻优求解,最后对列车进行加垫调簧作业和试验称重。主要结论为:
(1) 生产下线列车实测轮重偏差3位轴超限为4.13%,1位、2位、5位、6位动轴超限最大值为3.52%,4位、5位拖轴超限最大值为1.38%,算法指标值ζ算法为5.52%。
(2) 利用模拟退火算法计算5 000后趋于最优值,此时算法指标ζ算法降至1.99%;加垫位置共19个,最大加垫量为4 mm;通过加垫作业并测量轮轴重偏差值,最大轮重偏差为4位轴1.93%,满足4%规范要求;最大动轴偏差为1位轴1.99%,满足2%规范要求;最大拖轴偏差为0.17%,满足1%规范要求。
(3) 利用遗传算法计算40代后趋于最优值,此时算法指标ζ算法降至1.82%。加垫位置共17个,最大加垫量为4 mm;通过加垫作业并测量轮轴重偏差值,最大轮重偏差为6位轴1.6%,满足4%规范要求;最大轴重偏差为1位轴1.82%,满足2%规范要求;最大拖轴偏差为0.98%,满足1%规范要求。
(4) 模拟退火算法与遗传算求解的调簧方案均能将轮轴重偏差率降低至规定范围内。在调簧加垫之后模拟退火算法所得的轮重平均偏差率为1.198%,轴重平均偏差率为1.756%;遗传算法的轮重平均偏差率为1.115%,轴重平均偏差率为1.685%,遗传算法与模拟退火算法比较接近,对于调簧方案的寻优求解采用一般的成熟通用算法即可。
总体来看,利用所提出的加垫调簧方法,可一次性对五模块有轨电车的轮轴重偏差调平并满足规范要求,省去了车体、转向架、轮对的来回吊装拆卸,作业效率和调平精度显著提高。另外,利用该方法只需建立相应的联合刚度矩阵,即可方便的推广应用于其余各轨道车辆,这为轨道车辆的加垫调簧提供了理论支撑。
