基于自适应PID 参数的织机纱线张力控制系统研究

汪林俊 林富生 宋志峰 刘泠杉 龚小舟

（1.武汉纺织大学，湖北武汉，430200；2.三维纺织湖北省工程研究中心，湖北武汉，430200；3.湖北省数字化纺织装备重点实验室，湖北武汉，430200）

全自动三维平板织机因其制备工艺广泛、方法多样并突破传统二维织机的各种限制而备受关注，其织物基本织造工艺包括层间正交、角联锁等，因其强度高、抗刺抗冲击性能强而用于航空航天、军工、医疗等领域。在工作过程中，原料、设备、工艺过程等因素都会导致纱线张力不匀，造成纱线的物理机械性能损伤，织出的织物表面密度内外不一致、成形较差，多种不确定性以及现场工作环境的变化都会造成织机的纱线张力具有时变性［1］。目前，国内大部分纺织企业内部进行技术改造都加大了对智能织造工艺的研发，引入了传统工业PID 控制，然而效果并不理想，且加剧了织物经密的不均匀，纱线表面性能损伤大［2］，能够应用于全自动三维平板织机上的控制器更是少之又少。为解决这些问题，本研究设计了一种基于过拟合优化型的BP 径向基神经网络整定PID 参数控制纱线张力方法。

1 纱线张力控制原理

织机经纱张力控制系统是通过压力传感器采集纱线张力的大小，传感器将采集到的信号反馈到核心控制器STM32 单片机中，CPU 根据采集到的薄膜实际张力值与初始设定值之差，经过控制器计算后输出一定的模拟信号来控制张力执行机构的动作，从而调节纱线的张力使其无限接近目标值，对张力传感器测得的电压值进行A/D 转换［3］，采用屏幕显示张力的变化，最后能够使张力值维持在目标值附近很小波动。

2 织机纱线张力控制系统设计

传统织机张力控制方案是通过PID 实现闭环控制，结构较为简单，容易实现。根据三维织机工作时经纱张力不断变化的问题，通过张力采集器将纱线张力值进行转换后输送到芯片内部进行测量值与设定值比较，对误差进行比例、积分、微分处理［4］，将处理后的数据进行自适应学习后得出最优控制参数，实现对无刷直流电机的控制，从而完成对三维织机纱线张力的调节。

2.1 传统PID 控制器设计

传统PID 控制算法主要由比例系数KP、积分系数KI和微分系数KD组成［5］。对于纱线张力的校正，PID 控制器需要根据张力的输出反馈来确定对张力校正的强度。建立的纱线输送系统预测张力与实测张力存在偏差，PID 控制器根据传感器的反馈来纠正三维织机经纱张力偏差，从而实现实测张力与预测张力趋近一致，使织机经纱张力达到稳定的效果。

为了便于计算机运算，采用增量式PID 表达式［6］，如式（1）所示。

式中：e(t)为当前采样时刻的期望输出与实际输出之差，u(t)为当前采样时刻的控制量。

为了得到最终的第t次控制周期输入误差Δu(t)，需要使用历史偏差e(t-1)和e(t-2)，但此时并不是我们所需要的PID 输出量，因此对其偏差进行累加，则有式（2）。

由于经纱在整个三维织机织造中属于被动送经，张力控制受外界干扰波动且容易产生停滞性、非线性等缺点，采用常规数学模型无法进行准确分析［7］。

2.2 基于BP 神经网络整定的PID 控制器设计

传统PID 控制结构较为简单，对于张力传感器采集的数据处理也较为简单，无法实现准确的控制，因此需要对PID 的参数进行整定。采用BP神经网络算法的多层前向网络训练算法，提高收敛速度，简单易行、计算量小，可实现对PID 控制器参数整定［8-10］，不断逼近最优经纱张力值。

BP 神经网络PID 控制的具体结构如图1所示。

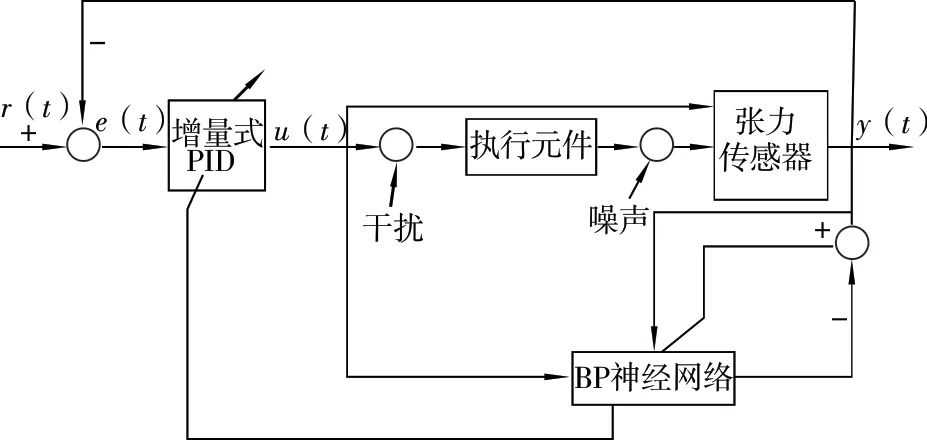
图1 基于BP 神经网络整定的PID 控制策略结构

BP 神经网络的结构选择4-5-3 型（即输入层含有4 个神经节点，隐含层含有5 个神经节点，输出层含有3 个神经节点），结构如图2 所示。其中，w是各层之间的权值，b是神经元本身的偏置。

图2 BP 神经网络整定PID 控制结构图

在常规BP 神经网络应用中，通过性能指标函数C(a，y)与权重、偏置的关系式来进行计算输出，即最后一层输入，如式（4）和式（5）所示。其中，a=σ(z)为激活函数Sigmoid 函数，其变化率σ'(z)在σ(z)逼近0 或1 时越来越小。

式中：C为代价，y为输出值，z为神经元输入。当σ(z)逼近0 或者1 时，变化率σ'(z)越来越小，当σ'(z)变化率减慢了，即变化率减慢，也就意味着学习速率下降。这时神经网络对于采集的PID 参数调节的作用几乎为零，基于BP 神经网络整定PID 参数的控制器对于经纱张力的精确控制微乎其微。

2.3 改进BP 神经网络整定的PID 控制器设计

为改进常用BP 神经网络函数存在调整效果缓慢而导致学习效率下降的问题，本研究采用交叉熵代价函数作为性能指标函数，如式（6）所示。此时，代价与权重关系式如式（7）所示。

从式（7）可知，此方法可消除σ'(z)与C(a，y)之间存在的影响，即σ'(z)变化率无影响，变化率不变，也就意味着学习速率不会下降。之后通过BP 神经网络各层之间的函数训练计算并处理后得到PID 控制器的参数KP、KI、KD［11-12］，采集的PID 参数调节时不会产生学习速率过慢的问题，对三维织机的经纱张力控制依旧保持一定的调节速率，整定PID 参数的样本数也在不断增加，可以稳定对经纱张力的调节。

3 张力控制模型仿真与结果分析

为验证本研究所设计的基于过拟合优化型BP 神经网络整定PID 参数控制算法对于张力参数的精确控制，对比传统PID 控制建立仿真结构如图3 所示。

图3 经纱张力控制Simulink 模型搭建图

根据经验和多次试验，取BP 神经网络的学习 速 率η为0.35，动 量 因 子α为0.05，权值w为（-1，1）区间内的随机数。张力的初始数据设定为100 cN，在Simulink 模型中0 时刻添加一个数值为100 的阶跃信号，可得到如图4～图6 所示的传统PID 控制、常规BP 神经网络整定PID 控制和基于过拟合优化的BP 神经网络PID 控制的仿真结果。

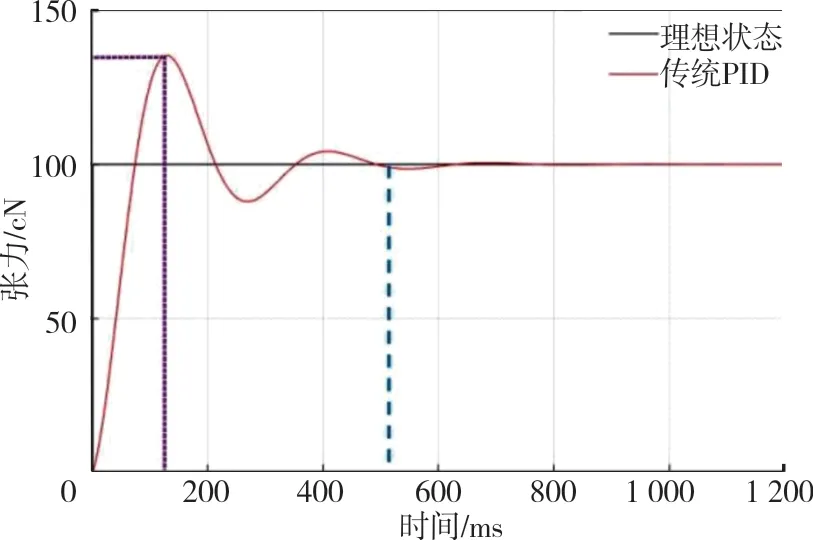
图4 传统PID 控制器张力变化曲线

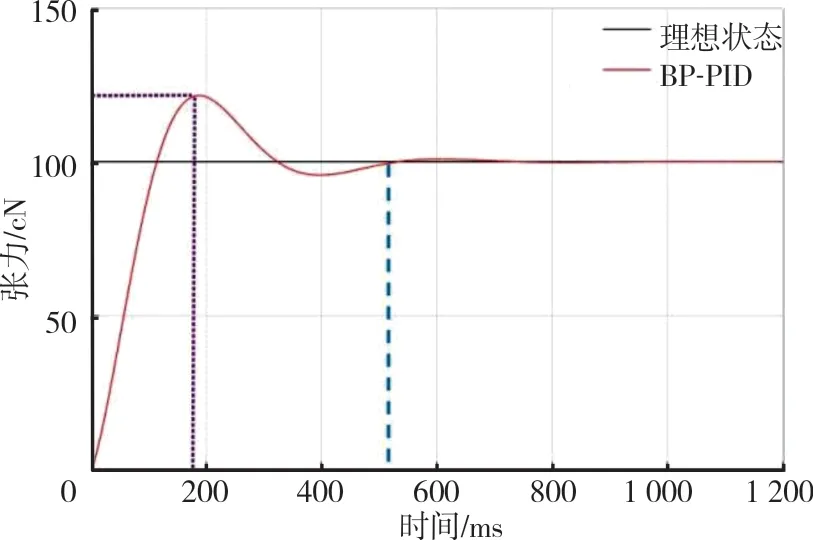
图5 常规BP 神经网络整定PID 张力控制曲线

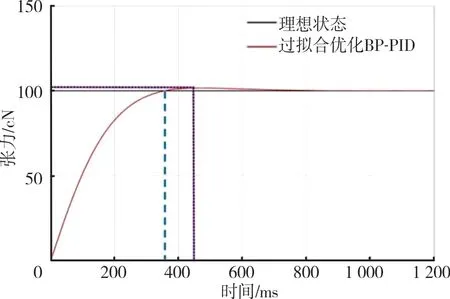
图6 过拟合优化BP 神经网络整定PID张力控制曲线

图4～图6 中，紫色虚线标注模型超调量和发生时间，蓝色虚线为模型趋向稳定位置。可知，采用传统PID 控制的张力系统中，张力输出的最大超调量达到35.7%，系统趋于稳定时间为0.5 s；采用常规BP 神经网络而不对其进行过拟合优化系统超调量达到24.8%，系统稳定时间为0.5 s；而采用过拟合优化的BP 神经网络PID 控制其张力输出曲线无明显超调（超调量小于5%），稳定时间在0.38 s。因此，采用过拟合优化的BP 神经网络PID 纱线张力控制系统具有更好的调整结果［13］，超 调 量 较 传 统PID 控 制 下 降 约30.7 个 百分点。

4 试验平台验证

在200 mm 幅宽的全自动碳纤维三维平板织物织机（武汉纺织大学自制）运行过程中进行试验（经纱出纱时张力范围在1.2 N～1.4 N，忽略纱线张力因小角度及过综眼时的影响），分别完成对传统PID 在线控制经纱的张力采集、常规BP 神经网络整定PID 参数控制经纱的张力采集和基于过拟合优化型BP 神经网络整定PID 参数控制经纱的张力采集，试验结果如图7 所示。

图7 对比张力采集曲线

根据图7 对比可看出，当使用过拟合优化型BP 神经网络调节PID 控制器时，经纱张力的离散率很小，经纱张力的峰值相对下降，同时谷值也相对提升，张力比较稳定，整个张力的超调量较小，基本上稳定在130 cN～150 cN 的理想范围之内；当使用传统PID 控制器或常规BP 神经网络调节PID 参数控制器时，系统所记录的纱线张力峰值高，同时谷值偏差大，说明纱线在织造时，时而绷紧，时而松散，不仅容易断裂，还容易使织物的经密不稳定，影响织物的组织结构。

5 结语

在全自动三维平板织机中，传统PID 控制器对经纱张力的控制效果远低于基于过拟合优化型BP 神经网络整定的PID 控制器对经纱张力的控制效果，无法使用在自动化程度要求高、织物质量要求严格的特种织物织机上。本研究采用过拟合优化型BP 神经网络整定PID 控制的设计方案，在仿真过程中纱线张力输出曲线无明显超调，超调量小于5%，稳定时间在0.38 s；在试验平台验证中，经纱张力的离散率很小，张力基本稳定在理想范围，对纱线张力的控制更加精确。但由于试验器材、机械结构限制，仍然存在一些不足，例如，采集器的灵敏度、数据传输通道选择等，后期将对这些不足进行研究修改，研发出更加精确的纱线张力控制器。