基于夹芯分层的碳纤维复材综框横梁仿真设计

邱海飞

（西京学院，陕西西安，710123）

在织造生产过程中，综框通过提拉纱线形成不同形状的梭口，长时间的高速往复运动，会使综框不可避免地承受交变载荷影响，进而导致其结构存在较大的疲劳破坏风险。例如，当织机主轴在800 r/min 车速下持续运转时，铝合金综框易出现疲劳性破坏与损伤，由此产生的疲劳裂纹甚至可能造成综框框架断裂，对于织机系统的安全稳定运行是极为不利的［1］。近年来，随着现代机织技术的高速高精化发展，新型无梭织机（如喷气织机、喷水织机）的车速已高达1 800 r/min，入纬率亦 高 达2 000 m/s［2］，这 种 情 况 下，现 代 机 织 设 备对于综框的综合工作性能提出了更高要求。

碳纤维复合材料具有比模量和比强度高、抗疲劳性强等诸多优点［3］。在复合材料综框的设计研发方面，一些国际知名厂商和纺织企业（如瑞士Grob 公司、美国Steel Heddle 公司、深圳泰纶公司等）已取得多项进展，并在实践应用中获得了良好评价与认可。同时，行业内的相关科技人员和高校工作者也在复合材料综框的技术探索方面做了不少尝试，例如：MARTIN B 等通过改进综框质量和结构刚性，设计研制出了一种适用于高速喷气织机的复合材料综框［4］。LEE D G 等采用刚度置换法、有限单元法、真空袋法及锤击法，对碳纤维复合材料综框进行了理论计算和试验研究［5］。孙亮等对碳纤维/环氧复合材料、铝合金和碳钢综框的工作性能进行了计算和分析［6］。霍福磊将混杂夹芯结构应用于新型综框的设计与制备，并研究了不同铺层方案和不同增强材料对于综框振动性能的影响［7］。以往研究和生产实践表明，由碳纤维复合材料制成的新一代综框，不仅能够将相同规格的综框质量减轻约25%，而且能够大幅降低开口系统惯性载荷与振动噪声，对于织机系统节约能耗、降低磨损具有重要现实意义。

综上，本研究提出了一种基于夹芯分层结构的碳纤维复材横梁，并通过有限元建模和动态仿真设计，对其承力性能及失效状态等进行深入探究，为碳纤维综框的轻量化设计与实践应用提供借鉴。

1 综框技术要求

综框是织机开口系统的核心运动部件，其主体结构呈平面框架形式，如图1 所示。一套完整的综框组件由多个零部件构成，其中，横梁与侧挡通过装配连接形成综框主体结构，而综丝、穿综杆、综丝夹及导板等则按照开口工艺要求配置于横梁和侧挡之上。在织物成形过程中，纱线通过综眼穿过综丝被分置于综框两侧，并在送经、卷取及开口运动综合作用下形成片纱梭口，进而为引纬和打纬运动做好准备。

图1 综框结构分解图

当综框长时间处于高速往复运动状态时，有可能引发一系列织造生产问题，如疲劳破坏、振动噪声及纱线张力波动等，不利于改善纺织车间环境和保护工人身心健康［8］。因此，理想的综框必须具备质量轻、强度高和耐疲劳性好等技术特点。

2 夹芯分层结构

考虑到剪切应力影响，夹芯结构等效力学模型分析常采用一阶剪切变形理论，其他相关理论（如Ressiner 理论、Hoff 理论）本质上均为夹芯板的一阶剪切理论。经典板壳理论认为，中面法线在板壳变形前后始终为直线且垂直于中面，而一阶剪切变形理论适用于薄板至中厚板，中面法线在变形后仍保持直线，但不一定与中面垂直。

复合材料夹芯结构一般由3 层介质构成，如图2 所示，xOy平面为夹芯结构中面，w为垂直于中面的芯材厚度方向（即z方向）。根据一阶剪切变形理论，描述夹芯板结构变形的位移场函数假设［9］如式（1）所示。

图2 夹芯结构示意图

式中：u、v、w为x、y、z坐标轴方向上的线性位移；φx、φy为转角位移；t为时间变量。

3 复材横梁设计

3.1 纤维层厚及方向

以ANSYS/WorkBench2020R1 为开发平台，通过其ACP（Pre）模块构建复材横梁数字化仿真模型。根据非对称层压板纤维铺层方案［0/45/-45/90/0/45/-45/90］°，采用复合材料库中的环氧碳纤维预浸布料（Epoxy Carbon UD 230 GPa Prepreg）进行铺层设计，如图3 所示。由于构成复材横梁的层压板基本单元Stackup 包含4层碳纤维，其纤维铺层方向为［0/45/-45/90］°，纤维铺设厚度为0.2 mm，则单个Stackup 单元的纤维铺层厚度为0.8 mm。因此，用于制备复材横梁的非对称层压板可认为是两个Stackup 单元的叠加组合，其总厚度为1.6 mm。

图3 基于预浸布料的非对称纤维铺层

考虑到轻量化和经济因素，可将复材横梁设计为夹芯结构，如图4 所示。

图4 复材横梁纤维铺层建模

其中，中间层选用正交各向异性弹性蜂窝芯材，外层纤维由两块非对称层压板黏合而成，纤维铺设方向如图中箭头所示。根据综框技术标准FZ/T 94009—2018《织机用铝合金综框》，设定横梁总厚度为12 mm，两侧纤维层厚为6.4 mm，中间层蜂窝芯材的厚度为5.6 mm。

3.2 承载计算

在织机开口运动过程中，综框会直接或间接承受不同动态载荷作用，如提综力、回综力及纱线张力等。对于消极式开口系统，需通过直吊弹簧来实现回综运动［10］。以综框上横梁为研究对象，忽略提综力影响，当综框运动至下限位置时，上横梁承载状态如图5 所示，此时，直接作用在上横梁上的载荷包括两部分，即弹簧回综力（F1、F2）和垂直方向的纱线张力（T≈q×L）。

图5 横梁下限位置承力简图

根据文献［10］，当单根吊综弹簧初伸长X0=80 mm 时，其实际设计刚度K=4 015 N/m。已知在梭口满开情况下，该开口系统的综框行程X≈145.6 mm，因此，可由式（2）计算得出单根弹簧的回综力F1=F2≈905.78 N。

以中平布纯棉平纹织物为织造对象，已知织物经纱号数为28 tex，经密ρf为251.5 根/10 cm。当梭口满开时，垂直方向上的纱线张力T会通过综丝或穿综杆传递至综框上横梁（见图5），这种情况下，可将纱线张力T近似等效为沿横梁长度方向的均布力q。

假设单根纱线张力p0≈20 cN/根，则可按式（3）所示方法近似计算作用于横梁上的最大片纱张力（Tmax）。已知综框幅宽L为190 cm，将各参数代入式（3）计算获得Tmax≈468.293 N，则等效均布力q≈246.47 N/m。

3.3 有限元模型

为进一步增强复合材料综框的承载性能，在其与xOz面平行的两侧表面分别黏合一根190 cm 长的铝合金板材，以此实现复材横梁的加固设计，如图6 所示。利用六面体单元分别对碳纤维层、蜂窝芯材及铝合金板材进行结构离散，网格划分结果共产生623 978 个单元和747 037 个节点。铝合金板材与复材横梁之间采用Bonded接触，以限制接触面边之间的切向和法向运动。

图6 复材横梁有限元模型

当综框运动至下限位置时，横梁处于瞬时静止状态。根据图5 所示承载状态设定边界条件，在横梁与侧挡接触的两个端面施加固定约束。同时，通过几何印记面处理在铝合金板材外表面设定加载区域，并将回综力F1、F2和均布载荷q分别加载至相应位置。复材横梁有限元建模材料性能参数如表1 所示。

表1 材料力学性能

4 静动态特性

4.1 应力与变形

通过复材横梁有限元静力学分析可知，在回综力F1、F2和等效均布力q综合作用下，复材横梁发生明显弯曲变形。如图7（a）所示，横梁变形幅度从中间弓形区域向两端逐渐减小，最大形变量仅约0.49 mm，对横梁刚性影响甚微。由图7（b）可知，横梁中间弓形区域的应力分布相对均匀，且应力值明显较小；而在靠近横梁两端位置附近区域存在较大应力分布，尤其是在回综弹簧悬挂处，尽管Von-Mises 应力已达到最大（约32.86 MPa），但远小于铝合金板材的抗拉/压屈服强度（280 MPa），不会对横梁结构造成破坏性影响。

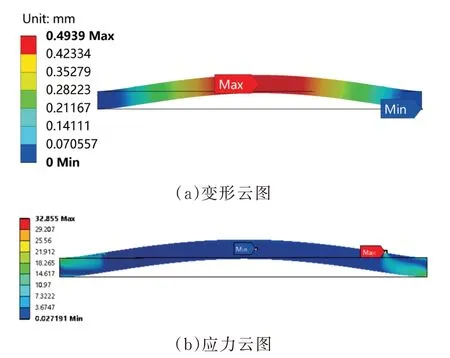
图7 静力学分析结果

4.2 模态分析

通过自由模态分析提取复材横梁的低阶固有频率及振型，如图8 所示。

图8 复材横梁振型

不计刚体模态，其1～5 阶固有频率范围在23.27 Hz～202.94 Hz，可见，这种含夹芯分层的碳纤维复材横梁至少能够适应1 200 r/min 以上的安全车速，对于现代高速织机的发展具有重要应用价值。比较各阶振型可知，复材横梁的振动模式主要以横向弯曲变形为主，且最大变形区域均出现在与侧挡连接的两端位置。因此，在设计制备复材横梁时，需结合实际适当增强横梁两端区域的强度和刚度储备，以提高综框的吸振及抗变形能力。

5 纤维层力学性能

5.1 数据继承与处理

在复材横梁几何建模、坐标装配及静力学分析基础上，将含夹芯碳纤维层的相关信息导入ACP（Post）后处理模块。通过不同层级的数据共享和链接，可使ACP（Post）继承前端流程的建模和仿真数据，如材料属性、几何模型、网格划分、边界条件及求解结果等。

5.2 层间应力

对于纤维增强复合材料，基体类型、层压板构成、纤维层厚及纤维铺设方向等均是影响其力学性能的重要因素［11］。通过在ACP（Post）中提取和对比分析各纤维层的应力状态，结果表明，具有相同铺层方向的纤维层，其应力分布也都基本相似。

以某Stackup 单元的纤维层应力状态为分析对象，如图9 所示，其纤维铺层方向为［0/45/-45/90］°。对比各层应力状态可知，0°纤维层和90°纤维层的应力分布具有典型对称特征，即横梁左右两端附近的应力大小和分布区域均相似，最大应力约在40 MPa 左右，如图9（a）、图9（d）所示；相比之下，45°纤维层和-45°纤维层只在横梁一端和弹簧悬挂点附近具有较明显的应力分布，如图9（b）、图9（c）所示，其最大应力约在50 MPa～63 MPa 之间，且这两种纤维层的应力分布区域也呈现一定对称性。

图9 纤维层应力状态

总体来看，各纤维层沿复材横梁长度方向的应力分布相对均匀，且应力值明显偏小（接近于0），而靠近横梁两端附近的应力波动较为活跃，尤其是在弹簧悬挂点附近，各纤维层在此区域均易发生应力集中，符合碳-铝复材横梁应力分析预期。

不同于两侧纤维层的应力状态，中间夹芯层的应力分布十分微小，如图10 所示。从图10 中可以看出，较为活跃的应力分布依然出现在横梁两端区域，且应力分布呈高度对称分布，最大应力仅为0.027 MPa，不会对蜂窝芯材的强度产生破坏性影响。

图10 夹芯层应力状态

5.3 失效分析

5.3.1 最大应力与应变准则

纤维增强复合材料失效准则是层压板强度设计计算的基础。理想的失效准则应尽量使用较少的失效参数，这对于各向同向材料而言较容易实现。由于碳纤维复合材料具有显著各向异性特征，其失效与载荷作用方向密切相关［12］。因此，实际当中需要更多的参数来描述其失效状态。

最大应力准则以应力值大小为失效衡量标准，当单向层压板中的各应力分量大于相应强度值时，复合材料便会发生失效破坏［13］。在拉、压承载条件下，其失效判据如式（4）～式（6）所示，这三个不等式相互独立，若其中一个不成立，即可判定材料失效。最大应变失效准则与最大应力失效准则相似，只是以极限应变作为失效约束。

式中：Xt为抗拉强度；Xc为纵向压缩强度；Yt为横 向 拉 伸 强度；Yc为 横 向 压缩强度；σ1、σ2分别为材料的第一、第二主方向应力；S为面内剪切强度；τ12为面内剪切应力。

5.3.2 纤维层失效分析

层压板的破坏是逐层发生的，当某一层在外加载荷作用下达到破坏极限时，该层将首先发生失效，而载荷则会重新分配至其余诸层，直至最后一层出现破坏［14］。由层间应力分析结果可知，弹簧悬挂点区域最易出现应力集中，因此，该区域也最易发生疲劳失效。

在ACP（Post）中创建基于最大应力的失效准则，提取弹簧悬挂点处的各纤维层失效状态，如图11 所示。对比分析可知，0°纤维层的逆向储备因子明显大于45°、-45°及90°纤维层，且各纤维层的失效活跃区按照0°、45°、-45°、90°依次减小，尤其是90°纤维层，其失效活跃区和逆向储备因子几乎为0。据此可知，在弹簧回综力作用下，各纤维层失效顺序为0°、45°、-45°、90°，90°纤维层具有相对较强的抗疲劳损伤特性。

图11 纤维层失效状态

为进一步明确失效区的应力状态，沿复材横梁厚度方向（z轴方向）提取其主应力分布曲线，如图12 所示。可以清楚地看到，主应力S1、S2、S3在中间层（蜂窝芯材）几乎为0 MPa，而在两侧的纤维层则发生了相对剧烈波动，尤其是主应力S1，波动幅度明显大于主应力S2、S3，说明主应力S1是造成复材横梁疲劳失效的主要因素。

图12 失效区主应力

6 结语

相对于传统综框，复合材料综框在减小织机系统振动、降低开口故障率和改善织物疵点等方面，具有可期的应用价值和发展前景。本研究设计了一种含夹芯分层的碳纤维复材横梁，并在WorkBench/ACP 环境下对其进行数字化建模和动态仿真，明确了横梁在回综力和纱线张力影响下的静动态特性、层间应力、芯材应力及纤维层失效状态等，对于复材横梁的设计制备及力学机理研究具有重要参考价值，同时也为碳纤维复合材料综框的设计创新提供了有力支持。