结合深度神经网络的大气压脉冲放电转化CO2研究
2023-09-19王绪成张远涛
王绪成,张远涛
(山东大学 电气工程学院,山东 济南 250061)
目前,CO2的过量排放打破了自然界的碳平衡,进而引发了一系列环境问题[1-4]。但CO2分子作为一种极其稳定的共价化合物,需要大量的能量输入才能打破其中的C=O键。目前工业中常用的热催化法需要高温和高压条件才能分解CO2,且存在能量损耗高、转化率低等问题[5]。低温等离子体(Low temperature plasma,LTP)作为一种高效的分子活化方法,近年来在将CO2转化为高价值化学品和燃料方面得到了极大的关注[6-8]。LTP不需要加热整个气体就可以获得大量的高能电子,可以通过电离、激发和解离等方式激活CO2,在室温和大气压下实现CO2的分解[9]。最近,脉冲电压驱动的介质阻挡放电(Dielectric barrier discharge,DBD)由于其独特的优势在CO2分解中得到了广泛的关注[10-11]。借助于脉冲电压快速变化的上升阶段,大气压脉冲DBD的能量效率更高,可以产生高能量、高密度的电子。流体模拟在分析CO2放电中扮演着关键的角色,被广泛应用于研究CO2放电特性和等离子体化学特性[12-13]。然而,在大气压CO2脉冲放电中,CO2的反应过程极其复杂,涉及到大量的激发粒子和数千个化学反应,这对流体模拟中空间网格和时间步长的选择提出了较高的要求。此外,传统的流体模型需要求解连续性方程、动量方程、电子能量守恒方程及泊松方程等微分方程,特别是在包含众多粒子和化学反应的情况下,每增加一种粒子,就需要增加求解一个连续性方程。尤其是针对脉冲放电,对时间步长及空间网格剖分要求更高,可以说计算效率较低。因此,流体模型在模拟大气压下脉冲电压驱动的CO2等离子体时面临着巨大的挑战,需要开发新的方法来提高计算效率。
最近几年,随着人工智能和计算机技术的快速发展,机器学习已经成功地被应用于各个领域[14-16]。而神经网络作为机器学习的一个子领域也得到了广泛的关注[17-18]。一个神经网络由输入层、隐藏层和输出层组成,其中输入层能够接受外部数据或信息并将其传递给隐藏层,输出层则产生对输入层所输入的外部数据或信息的预测[19]。当一个神经网络具有两个或两个以上的隐藏层时,被称为深度神经网络(Deep neural network,DNN)。目前,DNN已经被应用于各种等离子体工艺,例如等离子体蚀刻、表面改性和喷涂[20-22]。DNN可以直接从实验诊断和数值模拟中学习系统的内在规律,而无需预先了解系统动力学,这极大地提高LTP模拟的计算效率[23]。特别是当对CO2等离子体内复杂化学反应的理解有限时,DNN的这种特性就显得特别有价值。鉴于此,笔者使用流体模拟获得的数据对DNN进行训练,并利用训练后的DNN探究了脉冲上升率和坪区宽度对大气压CO2脉冲放电的影响。
1 实验装置及计算模型介绍
1.1 实验装置
图1给出了大气压下CO2脉冲放电的实验装置示意图。DBD装置由2个不锈钢的平行板电极组成,每个电极由厚度为1.0 mm的K9玻璃覆盖,放电间隙为2.0 mm。整个DBD装置放置于一个密封的反应器(长×宽×高=20 cm×20 cm×20 cm)。DBD装置的上电极由一个定制的纳秒脉冲发生器供电,下电极接地。采用流量控制器控制气体流量,将高纯度(体积分数99.99%)的CO2气体以流速1 L/min流入反应器中。在实验进行前,先用CO2气体将反应器冲洗至少3次以上,以减小其他气体杂质的影响。实验中的电压和电流信号由高压探头(型号Tektronix P6015A)和电流互感器探头(型号Magnelab CT-C2.5-SMA)测量,并由数字示波器(型号Tektronix MSO58 5-BW-1000)记录。此外,CO2等离子体的光学发射光谱通过光谱仪测量。

DBD—Dielectric barrier discharge图1 大气压CO2脉冲放电的实验装置示意图Fig.1 Schematic diagram of the experimental setup of atmospheric CO2 pulsed discharge
1.2 流体模型
本研究中将流体模型获得的大气压CO2脉冲放电的模拟数据作为DNN的训练集。在课题组前期的工作中,已对此流体模型的准确性进行了验证[24-25]。在流体模型中,使用连续性方程给出各种粒子的产生与消失,其动量方程由扩散漂移近似方程代替,使用泊松方程求解电场,利用电子能量平衡方程得到电子温度[26-27]。
(1)
(2)
(3)
(4)
式中:N为粒子的数密度,cm-3;Γ为粒子通量,(cm2·s)-1;S为粒子源项,(cm3·s)-1;q为粒子的电荷数;μ为迁移率,cm2/(V·s);D为扩散系数,cm2/s;E为电场强度,kV/cm;e0为基本电荷;ε0为真空介电常数;kb为玻尔兹曼常数;Qe为电子能量通量,eV/(cm2·s);ΔEj为反应j的能量损失,eV;kj为反应j的速率系数,(cm3·s)-1;kel为电子和背景粒子的碰撞频率;me和mg分别为电子和背景粒子的质量,g;Te为电子温度,eV;Tg为气体温度,K;下标i表示等离子体中的粒子i。
在流体模拟中,以2个平行板电极作为放电结构,每个电极由厚度为1.0 mm、相对介电常数为6.1的K9玻璃覆盖,放电间隙为2.0 mm,工作气压为大气压101325 Pa,气体温度为300 K。外加的脉冲电压(V(t))形式由式(5)所示的分段函数给出。
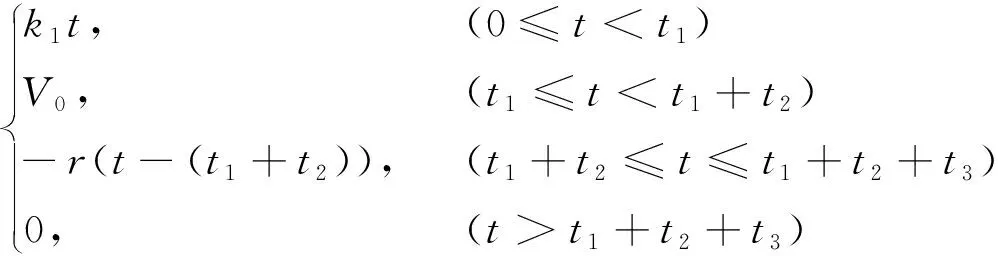
(5)
式中:r为脉冲上升率,V/ns,本研究中脉冲上升率始终与脉冲下降率相等;V0为外加脉冲电压的幅值,V;t1、t2和t3分别为脉冲上升时间、坪区时间和脉冲下降时间,ns。此外,本研究中的外加电压频率(f)固定为10 kHz。
1.3 DNN模型
基于CO2脉冲放电中复杂的电流行为[31-32],同时兼顾DNN在预测电场和产物粒子的空间分布时的通用性,本研究中构造了一个具有四层隐藏层的DNN,每个隐藏层包括30个神经元,如图2所示。该DNN是基于开源TensorFlow的具有GPU加速功能的全连接多层神经网络,采用误差反向传播算法[33-35]。该DNN由输入层、隐藏层和输出层组成。图2中的每个圆代表一个基本的计算单元,被称为神经元。
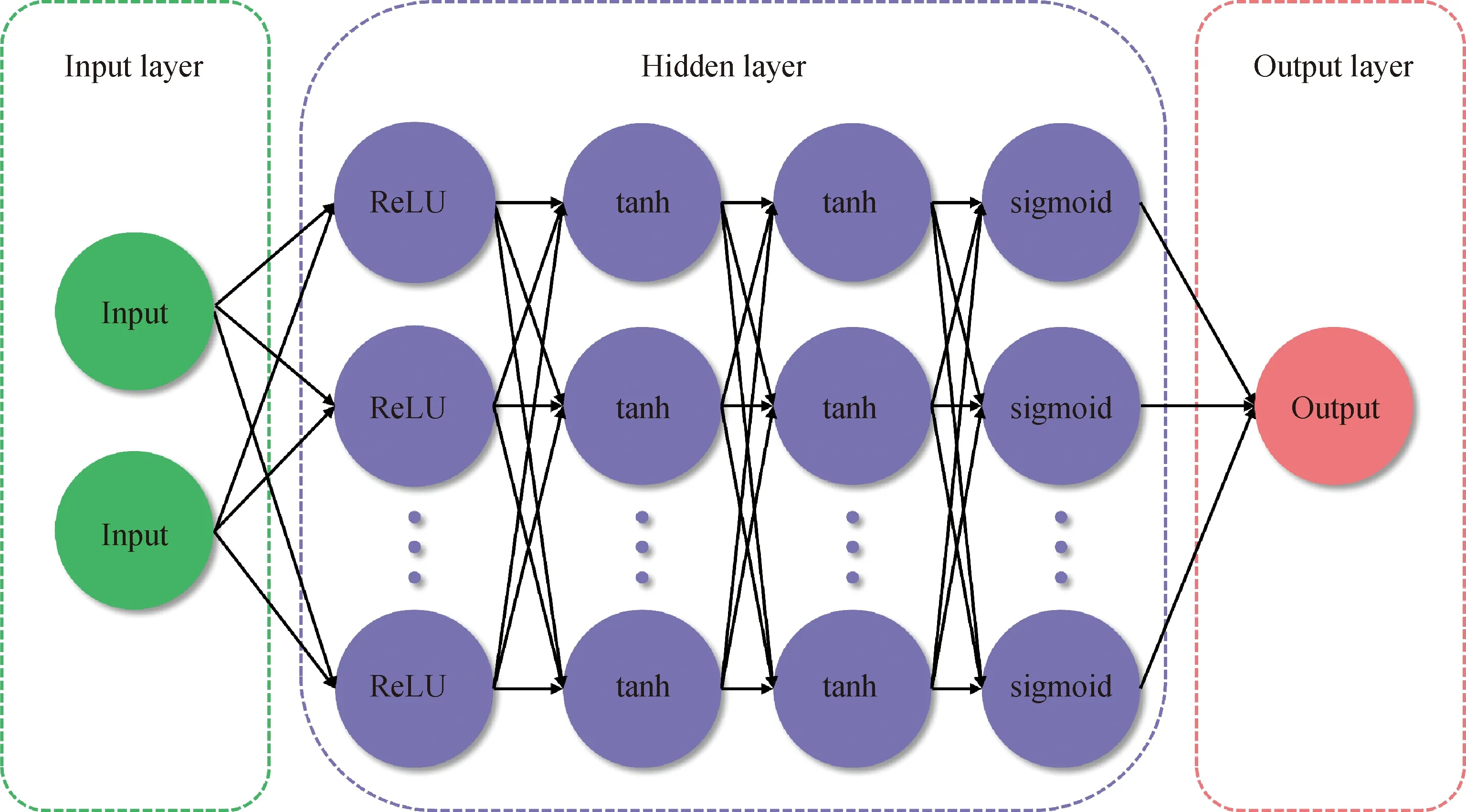
ReLU—Rectified linear unit;tanh—Hyperbolic tangent function图2 基于大气压CO2脉冲放电特性构建的DNN原理图Fig.2 Schematic map of DNN constructed based on the characteristics of atmospheric CO2 pulsed discharges
在DNN中,输入层和输出层的大小由输入和输出的维数决定。当探究电压上升率对CO2脉冲放电的电流密度的影响时,输入层的2个输入分别是时间和电压上升率,输出层的输出为DNN预测的电流密度。而在探究脉冲上升率对产物粒子空间分布的影响时,输入层的2个输入分别为空间位置和脉冲上升率,输出层为产物粒子密度。为了实现DNN对于CO2脉冲放电的电流密度、电场强度和产物粒子密度等多种放电特性的精准预测,4个隐藏层中依次采用线性整流(Rectified linear unit,ReLU)函数、双曲正切(tanh)函数、tanh函数和逻辑(sigmoid)函数作为激活函数。
在训练集的选择中,针对脉冲上升率变化的训练集在脉冲上升率为15~51 V/ns的范围内,每隔2 V/ns选取一组数据作为训练集,共19组训练集。针对脉冲坪区宽度变化的训练集在坪区宽度为450~850 ns的范围内,每隔20 ns选取一组数据作为训练集,共21组训练集。需要说明的是,在DNN算法中,训练集的选取和训练数据量的大小与DNN预测的准确率之间通常有密切的联系。在确定的参数范围内,训练集可以均匀选择,也可以随机选择。对于较为复杂的系统,可以通过增加训练集的数量来提高训练速度和预测准确性。此外,训练数据集的大小并不是固定的,可以随着训练数据的获得而进一步扩充。随着更多的数据被补充进入训练集,DNN的学习预测能力会进一步得到加强,但训练数据的增加同样会导致训练数据获取工作的计算量增加,甚至导致计算冗余[36]。
在对DNN进行训练之前,为避免不同的放电特征量之间存在的数量级差异对DNN优化造成困难,需要将训练数据集进行归一化[18]。随后,在DNN的训练过程中,构造了一个损失函数(L),通过最小化该损失函数来实现DNN的优化[37]。
(6)
式中:ns为在计算域中选择的散射点的数量;yp和ys分别为DNN的CO2放电的电流、电场和产物粒子密度等特性的预测结果和相应的流体模型结果。另外,为了直观地说明DNN模型的预测与流体模型的真实结果之间的误差,构造了一个相对误差(R)来验证DNN的有效性。
(7)
2 结果与讨论
2.1 DNN验证
DNN通过将CO2放电的电流、电场和产物粒子密度等特性的预测结果与相应的实验测量以及测试集内的流体模拟结果进行对比来验证DNN的有效性。在外加电压幅值为2000 V、驱动频率为10 kHz、脉冲上升时间为50 ns、坪区宽度为600 ns的条件下,图3给出了不同脉冲坪区宽度时,通过实验测量、流体模拟和DNN预测得到的放电电流的时间演化。从图3可以看出,实验测量、流体模拟和DNN预测的结果均表明,坪区宽度的增加会导致脉冲下降阶段放电强度增强,电流密度与流体模拟和DNN预测的电流密度之间的数值差异可能是实验中非理想的外加电压波形所导致的。此外,由于DNN模型是基于流体模拟结果训练的,所以图3(b)中流体模型获得的电流密度与DNN预测的电流密度的差值很小,即使在放电电流剧烈变化的区域,DNN预测结果与流体模拟结果的相对误差仅为0.41%。
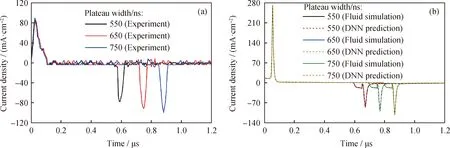
图3 不同坪区宽度下的大气压CO2脉冲放电的放电电流随时间的演化Fig.3 Temporal evolution of the discharge current of atmospheric CO2 pulsed discharge under various plateau widths(a)Experiment;(b)Fluid simulation and DNN predictionConditions:V0=2000 V;f=10 kHz;t1=50 ns;t2=600 ns
另外,在流体模型中,采用改进的Scharfetter-Gummel方法来求解控制方程。在上述的脉冲放电条件下,基于当前的计算机硬件参数(Intel Core i7-12700F CPU,16 G RAM),优化后的程序至少需要运行15个脉冲周期才能确保CO2放电的放电特性达到动态稳定(针对不同的放电参数,达到稳定所需的周期数可能更多),这大约需要30 h。而经过训练后的DNN可以在几秒内就给出预测结果,例如在计算放电电流时,在计算精度误差在0.4%的条件下仅需要7.5 s,比流体模拟的计算效率提高了将近5个数量级。可以说,DNN的应用在确保精度的条件下极大地提高了CO2脉冲放电的计算效率。
在外加电压幅值为2000 V、驱动频率为10 kHz、脉冲上升时间为50 ns、坪区宽度为600 ns的条件下,图4给出了DNN预测的电流密度峰值时刻带电粒子密度和电场强度的空间分布与流体模拟的对比,其中负电荷密度是电子和负离子密度之和。由图4可知:即使在电场和粒子密度变化较大的鞘层区域,DNN的预测效果也非常好;DNN预测的正电荷密度、负电荷密度、电子密度和电场强度的相对误差分别为0.16%、0.68%、0.13%和0.18%,相应的预测时间为6.8、7.2、7.5和6.7 s。结果表明,经过良好训练后的DNN程序能够准确地捕捉到大气压CO2脉冲放电的关键放电特征。

a1—Positive charge density (Fluid simulation);a2—Positive charge density (DNN prediction);b1—Negative charge density (Fluid simulation);b2—Negative charge density (DNN prediction);c1—Electron density (Fluid simulation);c2—Electron density (DNN prediction);d1—Electric field intensity (Fluid simulation);d2—Electric field intensity (DNN prediction)图4 DNN预测的电流峰值时刻的带电粒子密度和电场强度的空间分布与流体模拟结果的比较Fig.4 Spatial distributions of charged particle density and electric field intensity predicted by DNN at the peak current moment and comparison with the fluid simulation resultsConditions:V0=2000 V;f=10 kHz;t1=50 ns;t2=600 ns
在外加电压幅值为2000 V、驱动频率为10 kHz、脉冲上升时间为50 ns、坪区宽度为600 ns的条件下,将DNN预测的电流峰值时刻的各种产物粒子的空间分布与流体模型结果进行了比较,如图5所示。由图5可知:DNN预测的带电粒子密度与流体模型非常吻合,平均相对误差仅为0.86%,所需要的时间仅为7 s;DNN预测中性粒子密度和流体模拟具有较好的一致性,平均相对误差仅为0.126%,所需的时间仅为7.2 s;激发态CO2的平均相对误差仅为0.339%,预测时间仅为6.7 s。经过训练后的DNN能够迅速地描述大气压CO2脉冲放电的宏观和微观特性,特别是能快速地反映CO2放电中的等离子体化学特性,并且拥有很高的准确率。
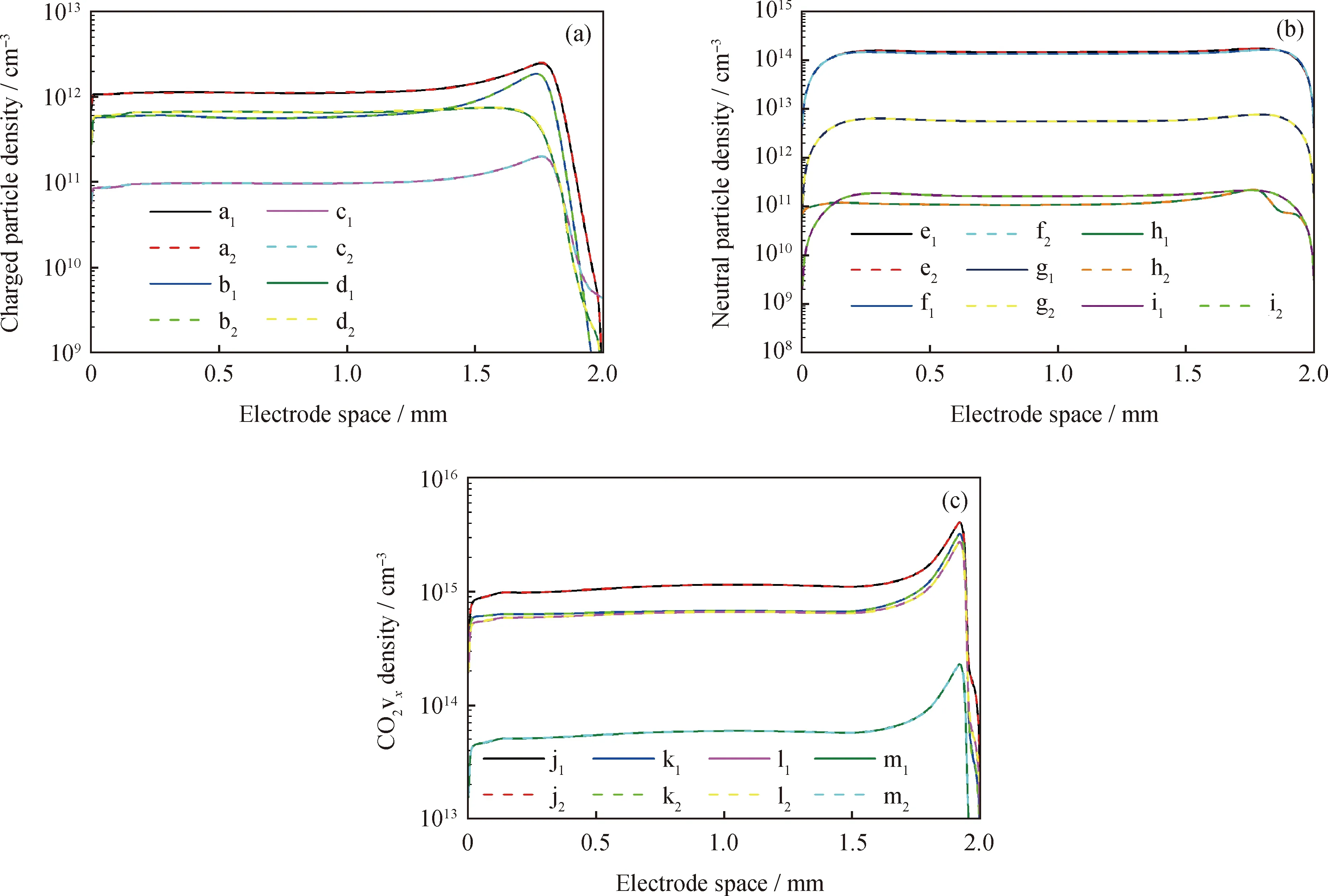
density (DNN prediction);b1—Electron density (Fluid simulation);b2—Electron density (DNN prediction); density (DNN prediction); density (DNN prediction);e1—CO density (Fluid simulation);e2—CO density (DNN prediction);f1—O density (Fluid simulation);f2—O density (DNN prediction);g1—O2 density (Fluid simulation);g2—O2 density (DNN prediction);h1—C density (Fluid simulation);h2—C density (DNN prediction);i1—O3 density (Fluid simulation);i2—O3 density (DNN prediction);j1—CO2v1 density (Fluid simulation);j2—CO2v1 density (DNN prediction);k1—CO2v2 density (Fluid simulation);k2—CO2v2 density (DNN prediction);l1—CO2v3 density (Fluid simulation);l2—CO2v3 density (DNN prediction);m1—CO2v4 density (Fluid simulation);m2—CO2v4 density (DNN prediction)图5 DNN预测的电流峰值时刻的产物粒子密度的空间分布与流体模拟结果的比较Fig.5 Spatial distributions of product particle density predicted by DNN at the peak current moment and comparison with the fluid simulation results (a)Charged particle density;(b)Neutral particle density;(c)Vibrationally excited CO2 densityConditions:V0=2000 V;f=10 kHz;t1=50 ns;t2=600 ns
2.2 脉冲上升率的影响
利用DNN探究了脉冲上升率对大气压CO2脉冲放电的放电特性和产物粒子的影响。经过良好的训练以后,DNN可以迅速给出15~50 V/ns之间的任意脉冲上升率下的CO2脉冲放电的特性。根据预测结果,在外加电压幅值为2000 V、驱动频率为10 kHz、坪区宽度为600 ns的条件下,图6给出了CO2脉冲放电的电压上升阶段的电流密度峰值和击穿电压随脉冲上升率的变化曲线。在本研究中,通过固定外加电压幅值而改变脉冲上升时间来改变脉冲上升率。从图6可以看到,电流密度峰值和击穿电压都随着脉冲上升率的增加而增加。

图6 DNN预测的峰值电流密度和击穿电压随脉冲上升率的变化曲线Fig.6 Variation curve of peak current density and breakdown voltage predicted by DNN as a function of pulse rise rate(a)Peak current density;(b)Breakdown voltageConditions:V0=2000 V;f=10 kHz;t2=600 ns
为了进一步探究大气压CO2脉冲放电的内在机制,图7给出了在外加电压幅值为2000 V、驱动频率为10 kHz、坪区宽度为600 ns的条件下,DNN预测的不同脉冲上升率下电流峰值时刻的电场强度的空间分布。当脉冲上升率增大时,阴极鞘层区域的电场明显增强,而等离子体区域的电场基本不变。由图7可知:增加脉冲上升率可以有效地强化电场,这会加速电子,提高鞘层附近的电离率;当脉冲上升率变化时,等离子体区和鞘层区的宽度基本不变。

图7 DNN预测的不同脉冲上升率下的电流峰值时刻的电场强度的空间分布Fig.7 Spatial distributions of the electric field predicted by DNN at the peak current moment under different pulse rise ratesConditions:V0=2000 V;f=10 kHz;t2=600 ns
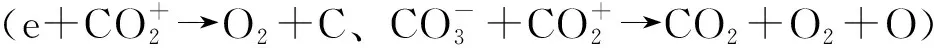

图8 DNN预测的电流峰值时刻的中性粒子产物的最大密度随脉冲上升率的变化曲线Fig.8 Variation curve of maximum densities of neutral particles predicted by DNN at the peak current moment as a function of the pulse rise rate(a)CO and O density;(b)O2 densityConditions:V0=2000 V;f=10 kHz;t2=600 ns
在CO2脉冲放电中,振动激发态CO2中的振动能量可以降低化学反应的能量壁垒,促进CO2的分解。因此,迅速而准确地获得振动激发态CO2的密度与脉冲上升率的关系就显得尤为重要。图9给出了在外加电压幅值为2000 V、驱动频率为10 kHz、坪区宽度为600 ns的条件下,利用训练后的DNN获得的电流峰值时刻不同振动激发态CO2的最大密度随脉冲上升率的变化曲线。由图9可以看出:当固定电压幅值时,脉冲上升率的增加可以有效地提高振动激发态CO2的密度;在脉冲放电阶段,电子碰撞激发过程是振动激发态CO2的主要产生路径[24]。随着脉冲上升率的增加,放电空间内的电子获得更多的能量,增强了电子碰撞激发过程,导致振动激发态CO2密度的增加。此外,由于CO2v1的振动激发阈值最低,更容易被激发,因此其密度也是最高的。总的来说,脉冲上升率的增加提高了振动激发态CO2的密度,这些激发态CO2相对于基态CO2更容易被分解,进一步提高了CO2的转化率。

图9 DNN预测的电流峰值时刻的激发态CO2的最大密度随脉冲上升率的变化曲线Fig.9 Variation curve of maximum densities of excited CO2 predicted by DNN at the peak current moment as a function of the pulse rise rateConditions:V0=2000 V;f=10 kHz;t2=600 ns
2.3 坪区宽度的影响

因此,笔者利用DNN预测了坪区宽度对CO2脉冲放电的放电特性和产物粒子的影响。经过训练以后,DNN可以给出坪区宽度450~850 ns之间的任意坪区宽度下的CO2脉冲放电的特性。在外加电压幅值为2000 V、脉冲上升和下降阶段的时间为50 ns、重复脉冲频率为10 kHz的条件下,图10给出了DNN预测的脉冲下降阶段的峰值电流密度随坪区宽度的变化曲线。从图10可以看出,脉冲下降阶段的放电电流峰值随着坪区宽度的增加而线性增加。
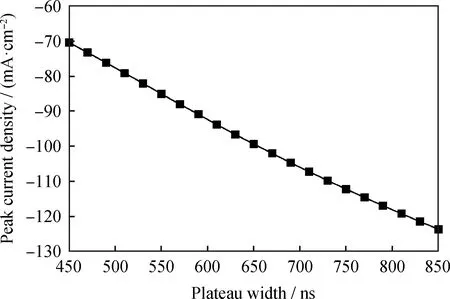
图10 DNN预测的脉冲下降阶段的峰值电流密度随坪区宽度的变化曲线Fig.10 Variation curve of peak current density predicted by DNN during the pulse fall phase as a function of the plateau widthConditions:V0=2000 V;f=10 kHz;t1=50 ns

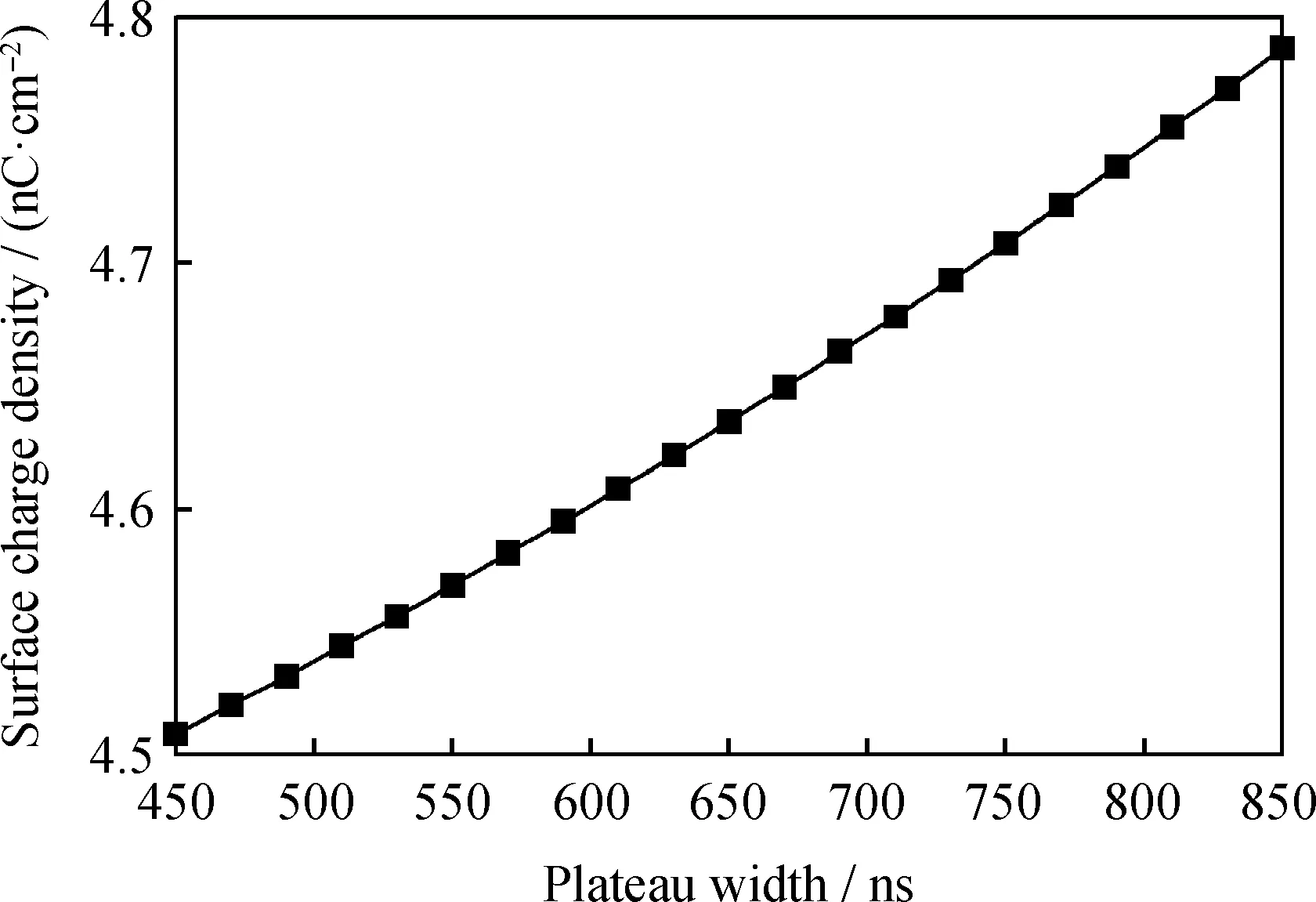
图11 DNN预测的最大表面电荷密度随坪区宽度的变化曲线Fig.11 Variation curve of maximum surface charge density predicted by DNN as a function of the plateau widthConditions:V0=2000 V;f=10 kHz;t1=50 ns
在外加电压幅值为2000 V、重复脉冲频率为10 kHz、脉冲上升时间为50 ns的条件下,图12给出了DNN对于放电空间内最大电场随坪区宽度的变化曲线的预测。由图12可以看出,在给定的脉冲下降率下,随着坪区宽度的增加,放电空间内的电场明显得到增强。根据预测结果,可以清楚地看出电场与坪区宽度的关系几乎是线性的,坪区宽度的提高导致了电场强度的增加,强电场会提高电子碰撞反应的速率,导致产物粒子密度的上升。

图12 DNN预测的脉冲下降阶段电流峰值时刻的电场强度的最大值随坪区宽度的变化曲线Fig.12 Variation curve of maximum value of electric field predicted by DNN at the peak current moment during the pulse fall phase as a function of the plateau widthConditions:V0=2000 V;f=10 kHz;t1=50 ns
在外加电压幅值为2000 V、重复脉冲频率为10 kHz、脉冲上升时间为50 ns的条件下,图13给出了DNN预测的脉冲下降阶段的放电电流峰值时刻CO、O和O2的最大密度随坪区宽度的变化曲线。预测结果清楚地表明,改变坪区宽度可以通过影响脉冲下降阶段的放电强度来影响产物粒子的密度。总的来说,坪区宽度的增加可以有效增强脉冲下降阶段放电空间内的电场,强电场会加速电子碰撞解离反应和电子碰撞吸附反应的速率,导致CO和O密度的增加。此外,强电场还可以促进电离反应产生更多的电子和离子,这些电子和离子可以进一步相互反应,产生更多的O2。图13的结果表明,当固定脉冲电压波形而提高坪区宽度时,会使脉冲下降阶段产生更剧烈的放电,导致在脉冲下降阶段更多的CO2分解为CO、O和O2等,这会进一步提高CO2的转化率。

图13 DNN预测的脉冲下降阶段电流峰值时刻的CO、O和O2的最大密度随坪区宽度的变化曲线Fig.13 Variation curve of maximum densities of CO,O,and O2 predicted by DNN at the peak current moment during the pulse fall phase as a function of the plateau widthConditions:V0=2000 V;f=10 kHz;t1=50 ns
随着坪区宽度的增加,放电空间内的带电粒子会在空间电场的驱动下持续地向电极运动并在介质板表面累积,导致介质板表面上的电荷密度增大,而放电空间内剩余带电粒子的密度减小。这说明如果坪区宽度足够大,放电空间内的带电粒子密度会减小到一个很小的值,当继续增加坪区宽度时,介质板上的表面电荷密度将不会再增加,同时坪区宽度的增加对脉冲下降阶段的放电也没有明显的影响。经过计算,发现当坪区宽度超过15000 ns时,介质板表面电荷密度将保持在5.4 nC/cm2几乎不变,而脉冲下降阶段的放电电流密度保持在-314 mA/cm2几乎不变。
3 结语与展望
在本研究中,DNN始终都是单变量输入,而事实上DNN本身是支持多变量输入的,例如同时考虑电压幅值、脉冲上升率和间隙宽度等参数的变化。但多变量输入的DNN需要大量的训练数据进行训练,这对计算设备的计算能力提出了更高的要求。在以后的工作中,可以考虑采用分段训练或者小样本训练的方法以降低多变量输入DNN对设备计算能力及数据量的要求。此外,使用目前的DNN算法可能难以预测多电流峰值和非线性放电行为等复杂的等离子体放电行为,可以通过调整DNN的隐藏层或神经元的数量来解决这一问题,这也是笔者未来需要进行的工作。
