三力平衡问题的求解策略———以“轻绳、轻杆模型”为例

■山东省临沂第十八中学 张 宇

■山东省临沂第十九中学 夏宗平

共点力平衡是指物体受到几个力的作用处于平衡状态,即处于静止或匀速直线运动状态。三力平衡是共点力平衡问题中的一个考查热点,也是难点,求解三力平衡问题对同学们的理解能力、空间想象能力、逻辑推导能力和应用数学知识解决物理问题能力的要求都较高。下面以“轻绳、轻杆模型”中的三力平衡问题为例,论述如何透过表面现象,抓住各种题型的本质特征,找到相应的解题方法,供同学们参考。

一、三力静态平衡问题

例1如图1所示,水平轻杆BC的B端用铰链固定在竖直墙壁上,轻绳AD拴接在轻杆C端,D端所挂物体质量为m,轻绳AC段与水平方向间的夹角α=30°,取重力加速度g=10 m/s2,求轻绳AC的拉力T的大小,以及轻杆BC对结点C的支持力N。

图1

指点迷津：本题是平衡问题中典型的死结、活杆模型,以结点C为研究对象,分析轻绳时要特别注意轻绳AC段是拴接在C点的,其拉力不等于物体的重力,分析轻杆时要特别注意与铰链相连的杆上的作用力一定沿杆的方向。

解法1：力的合成法。对结点C进行受力分析,以T和N为邻边作平行四边形,其对角线与mg大小相等,方向相反,如图2所示。根据几何关系得,方向水平向右。

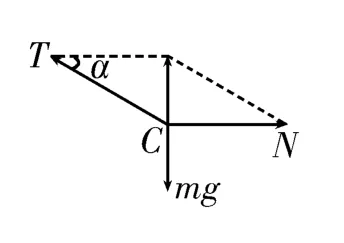
图2

解法2：正交分解法。对结点C进行受力分析并正交分解,如图3 所示。根据几何关系得Tx=Tcosα,Ty=Tsinα。根据平衡条件得Tx=N,Ty=mg。联立以上各式解得,方向水平向右。

图3

点评:已知三个力的方向且其中两个力存在垂直关系是三力静态平衡问题中最常见的题型。解题时既可以利用力的合成法,先构建平行四边形找到直角三角形,再利用三角函数关系进行求解;也可以利用正交分解法,先以相互垂直的两个力的方向为x、y轴建立平面直角坐标系,将不在坐标轴上的那个力分解到坐标轴上,再利用平衡关系进行求解。

变式1：如图4 所示,轻杆BC的B端用铰链固定在水平地面上,轻绳AD拴接在轻杆C端,D端所挂物体质量为m,轻绳AC段与水平方向间的夹角α=30°,轻杆BC与水平方向间的夹角β=45°,取重力加速度g=10 m/s2,求轻绳AC的拉力T的大小,以及轻杆BC对结点C的支持力。

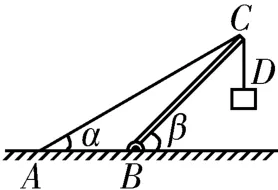
图4

答 案：,方向与水平方向成45°角斜向右上方。 提示:已知的三个力不存在某两个力的方向始终垂直的关系,无法构建直角三角形,但可以用正交分解法进行求解。对结点C进行受力分析并正交分解,如图5所示。根据几何关系得Tx=Tcosα,Ty=Tsinα,Nx=Ncosβ,Ny=Nsinβ。根据平衡条件得Tx=Nx,Ny=Ty+mg。联立以上各式解得,方向与水平方向成45°角斜向右上方。

图5

变式2：如图6 所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮悬挂一个质量为m的物体,轻绳AC段与水平方向间的夹角α=30°,取重力加速度g=10 m/s2。求轻绳AC段的张力T的大小,以及横梁BC对C点的支持力。

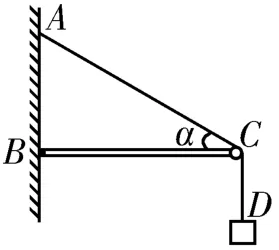
图6

答案：T=mg;N=mg,方向与竖直方向成60°角斜向右上方。 提示:已知两个力的大小和方向且两个力存在相等关系,而第三个力的方向未知,用力的合成法构建菱形可知第三个力一定在前两个力的角平分线上,根据三角形的边长关系即可求出第三个力的大小。对C点进行受力分析,则T=mg,以T和mg为邻边作平行四边形,其对角线与N大小相等,方向相反,如图7 所示。根据几何关系得N=mg,方向与竖直方向成60°角斜向右上方。

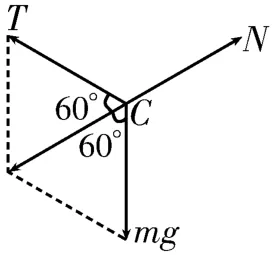
图7

二、三力动态平衡问题

例2如图8所示,用轻绳OA、OB悬挂一物体处于平衡状态,轻绳OA与竖直方向成一夹角,轻绳OB水平。当轻绳OA的悬点A缓慢向右移动时,轻绳OB始终保持水平。设此过程中轻绳OA、OB的拉力分别为FOA、FOB,下列说法中正确的是( )。

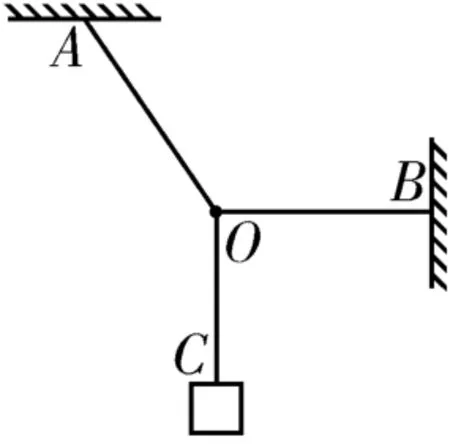
图8

A.FOA一直减小

B.FOA先减小后增大

C.FOB一直减小

D.FOB先增大后减小

指点迷津：在对O点进行受力分析时要特别注意当轻绳OA的悬点A向右移动时,FOC的大小和方向均不变,FOB的方向不变,FOA的方向发生变化,需要抓住“变化“与“平衡”间的关系。

解法1：解析法。对初状态O点进行受力分析,设FOA与竖直方向间的夹角为θ,以FOA和FOB为邻边作平行四边形,其对角线与mg大小相等,方向相反,如图9 所示。根据几何关系得。当轻绳OA的悬点A缓慢向右移动时,θ减小,根据三角函数的单调性得FOA一直减小,FOB也一直减小。

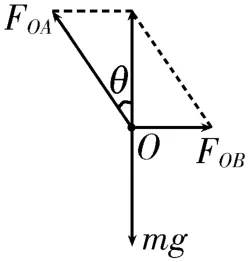
图9

解法2：图解法。以初状态O点为研究对象,其受到的mg、FOA、FOB可构成矢量三角形,如图10 所示。当轻绳OA的悬点A缓慢向右移动时,FOA与竖直方向间的夹角减小,需要将FOA的方向绕重力的末端沿顺时针方向旋转形成新的矢量三角形,观察变化的矢量三角形可以看出FOA、FOB均逐渐减小。

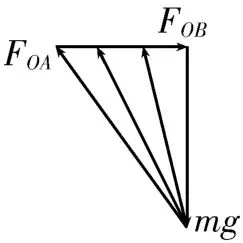
图10

答案：AC

点评:本题是三力动态平衡问题中一个力的大小和方向均不变,一个力的方向不变,一个力的方向发生变化类题型。因为三个力中FOB和mg始终存在垂直关系,所以既可以利用力的合成法,先构建平行四边形找到直角三角形,再利用三角函数的单调性进行求解;也可以利用图解法,将三力首尾相连构成矢量三角形,当FOA方向发生变化时比较矢量三角形线段的长度变化即可判断力的变化情况。

变式3：如图11所示,用轻绳OA、OB悬挂一物体处于平衡状态,开始时轻绳OB水平。现保持O点位置不变,改变轻绳OB的长度使轻绳右端由B点缓慢上移至B'点,此时轻绳OB'与OA之间的夹角θ＜90°。设此过程中轻绳OA、OB的拉力分别为FOA、FOB,下列说法中正确的是( )。

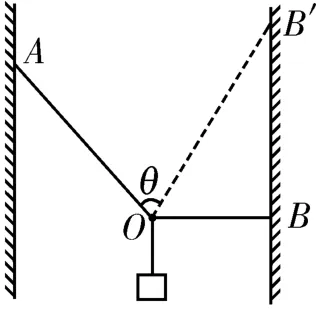
图11

A.FOA一直减小

B.FOA一直增大

C.FOB一直减小

D.FOB先增大后减小

答案：A 提示:虽然FOB的方向发生变化,使得三个力不存在某两个力的方向始终垂直的关系,无法构建直角三角形,但可以用图解法进行求解。以初状态O点为研究对象,其受到的mg、FOA、FOB可构成矢量三角形,如图12所示。当B点缓慢向上移动时,FOB与竖直方向间的夹角减小,需要将FOB的方向绕重力的末端沿逆时针方向旋转形成新的矢量三角形,直至FOA与FOB之间的夹角小于90°,观察变化的矢量三角形可以看出FOA逐渐减小,FOB先减小后增大。

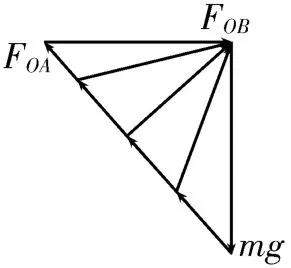
图12

例3如图13所示,轻绳与轻杆承受弹力的最大值一定,轻杆的C端用铰链固定,光滑轻小滑轮在C点正上方,B端吊一重物,现将轻绳的一端拴在轻杆的B端,用拉力F将B端缓慢上拉,在轻杆BC达到竖直前(轻绳与轻杆均未断),关于轻绳的拉力FAB和轻杆受到的弹力FBC的变化,下列说法中正确的是( )。

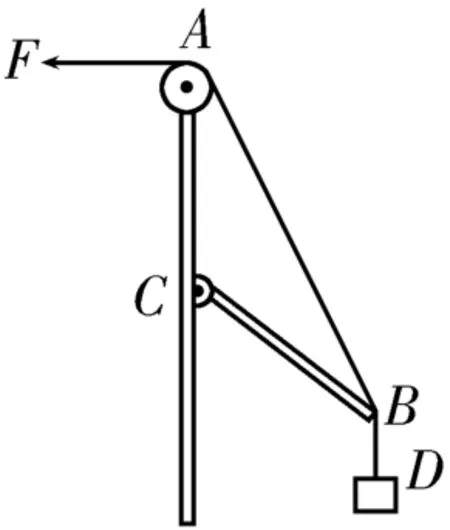
图13

A.FAB增大 B.FAB减小

C.FBC增大 D.FBC减小

指点迷津：在对B点进行受力分析时要特别注意将B端缓慢上拉时,FBD(等于重物的重力)的大小和方向均不变,FAB和FBC的方向均发生变化,需要找到图中暗含的空间几何三角形和力的矢量三角形的相似关系。

解析：对结点B进行受力分析,以FAB和FBC为邻边作平行四边形,其对角线与mg大小相等,方向相反,如图14 所示。根据空间几何三角形ABC与力的矢量三角形相似得。将B端缓慢上拉的过程中,AC、BC边的长度不变,AB边的长度减小,所以FBC不变,FAB减小。

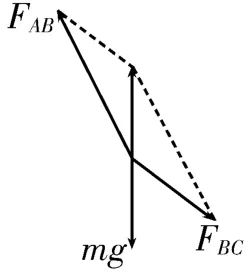
图14

答案：B

点评:本题是三力动态平衡问题中一个力的大小和方向均不变,另外两个力的方向均发生变化类题型。需要在正确受力分析的基础上先作出平行四边形,再找到相似的几何三角形与力的矢量三角形,由对应边成比例写出等式进行计算、推理即可得出答案。

变式4：如图15 所示,装置中两根细绳拴住一小球,保持两细绳间的夹角θ=120°不变,若把整个装置沿顺时针方向缓慢转过90°,则在转动过程中,关于两细绳的拉力FCA和FCB的变化,下列说法正确的是( )。

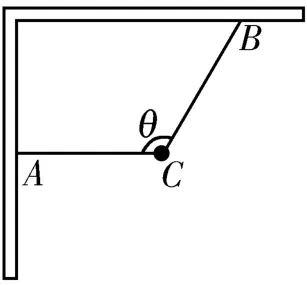
图15

A.FCA先减小后增大

B.FCA先增大后减小

C.FCB先减小后增大

D.FCB一直减小,且最终减小为零

答案：BD 提示:在装置缓慢转动的过程中,小球重力mg的大小和方向均不变,FCA和FCB的方向均发生变化但它们的夹角始终保持不变,可以利用“同圆中同弦所对的圆周角相等”建构一个辅助圆进行求解。以初状态小球为研究对象,其受到的mg、FCA、FCB可构成矢量三角形,画矢量三角形的外接圆,保持恒力mg这条弦不变,在CA由水平方向缓慢转到竖直方向的过程中,保持FCA与FCB的夹角不变,画出三个力动态平衡的矢量三角形,如图16 所示。由图可以看出,FCA先增大后减小,FCB一直减小,且最终减小为零。

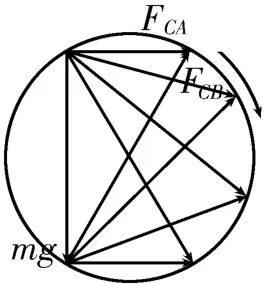
图16