基于邻域搜索的改进反向学习平衡优化器算法
2023-09-18李安东苟茹茹
李安东,刘 升,苟茹茹
(1.上海工程技术大学管理学院,上海 201620;2.河北大学网络空间安全与计算机学院,河北 保定 071002)
1 引言
平衡优化器EO(Equilibrium Optimizer)是Faramarzi等人[1]于2020年提出的一种新型智能算法,用于描述控制体积内质量动态平衡的过程。设定浓度平衡池,各浓度朝平衡池动态平衡的过程就是种群收敛于全局最优解的过程。与遗传优化算法和鲸鱼优化算法等利用多种机制进行位置更新的群智能算法相比,EO算法具有结构简单、灵活性高的特点。已被学者进一步地应用于调度优化等工程问题中,再次证明了EO算法卓越的寻优性能。但是,EO算法的整个迭代过程只依赖于一个质量平衡公式更新浓度,种群极易陷入局部最优解;前期平衡池内部浓度差异较大,会影响种群的收敛速度。针对上述算法的不足,Naik等人[2]通过添加小逃跑概率机制并结合反向学习策略进行全方位探索,提出反向平衡优化器OEO(Opposition Equilibrium Optimizer)算法,测试结果表明OEO具有较好的寻优性能;Tang等人[3]提出了一种多种群体混合平衡优化器MHEO(Multiple Population Hybrid Equilibrium)算法,该算法将种群依次分为探索、开发和平衡3个子种群,分别执行不同的搜索机制帮助种群跳出局部最优,CEC2017测试函数结果显示,改进算法寻优性能有较大提升;Wunnava等人[4]提出一种自适应均衡优化器AEO(Adaptive Equilibrium Optimizer)算法,通过粒子适应度值和全体粒子平均适应度值的比较,随机更新当前粒子浓度。上述改进算法虽然提高了EO算法的性能,但是收敛精度还可进一步提高。
为此,本文根据迭代过程的不同特点,从平衡池、质量平衡方程和全体粒子扰动3方面,分别利用双曲正切算子、邻域拓扑搜索机制和动态对称反向学习策略进行改进,提出一种结合邻域拓扑搜索改进的反向平衡优化器IOLEONS(Improved Opposition-based Learning Equilibrium Optimizer algorithm based on Neighborhood Searching)算法。基准函数和工程优化问题的模拟测试结果表明,IOLEONS算法具有较高的收敛精度和收敛速度。
2 标准EO算法
2.1 种群初始化
平衡优化器算法的浓度初始化过程表述如式(1)所示[1]:
Ci,j=Cmin,j+rand*(Cmax,j-Cmin,j)
(1)
其中,Ci,j表示粒子i在第j维的浓度值,Cmin,j表示第j维所有粒子浓度的最小值(下限),Cmax,j表示第j维所有粒子浓度的最大值(上限),rand为[0,1]的随机数。
2.2 建立平衡池和设置候选解
EO算法达到的最优状态即浓度平衡状态,其中平衡池是由适应度值较高的前4个粒子及其中心粒子组成,这5个粒子即为下一次迭代的目标候选解。平衡池的浓度表示如式(2)所示[1]:
Ceq,pool={Ceq(1),Ceq(2),Ceq(3),Ceq(4),Ceq(ave)}
(2)
(3)
其中,Ceq,pool表示浓度平衡池,Ceq(i),i=1,2,3,4分别为依适应度值逆序排列的候选解,Ceq(ave)表示平衡池的平均候选解。
2.3 浓度更新
建立平衡池后,EO算法开发和探索阶段的转换主要依靠指数项(F)指导。指数项(F)是一个随迭代次数变化的时变控制变量,具体表示如式(4)所示[1]:
F=e-λ(t-t0)
(4)
(5)
(6)
其中,λ各维分量均为[0,1]的随机数,t与迭代次数有关,iter为当前迭代次数,max_iter为最大迭代次数,通常取a2为1,a1为2,sign(·)为符号函数,r各分量为[0,1]的随机数。
式(4)与式(6)联合得指数项F如式(7)所示:
F=a1sign(r-0.5)[e-λt-1]
(7)
此外,为进一步增强算法开发能力,标准EO算法引入生成率(G)提升可行解的精度,如式(8)所示[1]:
G=G0e-λ(t-t0)
(8)
G0=GCP(Ceq-λC)
(9)
(10)
其中,r1和r2均为[0,1]的随机数;G0表示初始生成率;GP表示生成概率,通常取常数0.5;Ceq表示从平衡池中随机选择的候选解;GCP的各分量GCPl由式(10)得出。
综上所述,标准平衡优化器算法的每个个体的浓度C迭代更新公式如式(11)所示:
C=Ceq+(C-Ceq)*F+(G/(λV))(1-F)
(11)
其中,V表示单位体积。
标准EO算法伪代码如算法1所示,其中N表示种群规模。
算法1标准EO算法
设置参数;
初始化粒子种群;
Whileiter Fori=1:N 计算全体粒子适应度值并选出最优粒子; Endfor 依据式(2)和式(3)建立平衡池; Fork=1:N 从平衡池中随机选择候选解; 随机生成λ和r; 依据式(4)~式(7)计算F; 依据式(8)~式(10)计算G; 依据式(11)更新浓度值; Endfor t=t+1; Endwhile 为了解决标准EO算法存在的性能缺陷问题,本文依次从平衡池、质量平衡方程和粒子自适应扰动等方面进行改进,具体改进方法如下所述。 标准EO算法的一个显著特点就是设置平衡池,并从中随机选择粒子作为平衡浓度(候选解),以此平衡探索和开发。但是,由于种群空间分布的不确定性,迭代前期种群较为分散,降低了种群收敛速度;迭代中期种群分布较为集中,极易引导种群陷入局部最优解;迭代后期使用算数平均计算出的平均浓度中最优粒子浓度所占的比重较低,进而降低了收敛精度。为此文献[5]通过柯西分布修改角频率并利用正弦函数改进平衡池。正弦池策略着重于平均浓度前的系数的改进,然而这易使新的平均候选解跳出原平衡池的边界约束,降低迭代前期的收敛速度。为避免以上问题,本文对平均候选解的改进如式(12)和式(13)所示: (12) (13) 其中,ht为双曲正切算子,abs()为求绝对值运算,tanh(·)为双曲正切函数。 由图1可知,迭代前期平均候选解中最优浓度值占比较大,且占比缓慢降低,加快了前期的收敛速度;迭代中期,较低的占比保证了全局的充分探索,可降低陷入局部最优解的风险;迭代后期,较高的占比和缓慢的增长速度,提高了种群对于目标区域的开发能力,从而提高收敛精度。 Figure 1 Hyperbolic tangent diagram EO算法中最重要的部分当属浓度更新方式。分析式(10)可知,在r2 C=Ceq+(C-Ceq)*F*r1+ (G/(λV))(1-F)+(1-r1)* (local_leader_pos(i)-Ceq) (14) 其中,r1为随机向量,各分量为[0,1]的随机数;local_leader_pos(i)是与粒子i相邻的m个粒子中适应度值最高的粒子,设置距离计算方式为欧氏距离,其空间示意图如图2所示。 Figure 2 Diagram of neighborhood searching 图2所示为m=5时确定的邻域范围,以粒子所在位置为中心计算其与其他粒子的欧氏距离,从而选定邻域领导者。从图2中粒子运动的2个方向不难看出,通过引入邻域领导者粒子,引导粒子朝向所在邻域内的领导者移动,降低粒子逼近于均衡浓度的速度,加强对于邻域的探索,提高了种群的局部开发能力。 元启发式优化算法是一种模拟自然智慧而建立的随机优化算法,常见的有遗传优化算法、蚁群算法等。因该类算法中个体进化方向具有不确定性,从而使得算法具有更多的求解机会。尽管进化规则略有不同,但是迭代后期种群一般呈现出聚集性高的局面,这便加剧了种群陷入局部最优解的风险。 EO算法迭代至后期时,由于平衡池浓度差较小,种群则聚集于平衡池附近,种群呈现出分散度差的局面,为提高种群多样性,需采取一定的扰动策略。文献[7]利用反向学习策略改进鲸鱼优化算法来提高种群多样性。然而,基本的反向学习策略仍存在搜索能力不足和种群多样性差的缺点[8],仍需进一步改进。本文通过引入Chebyshev映射增强粒子的空间遍历性,提高种群的分散程度;利用随机权重融合动态边界和固定边界改进反向学习策略,提升种群对于开发区域的专注度。映射公式表示如式(15)~式(17)所示: x(n)∈[-1,1] (15) Da(i)=(1-r3)*min(Ci)+r3*lb (16) Db(i)=(1-r3)*max(Ci)+r3*ub (17) 其中,r3表示[0,1]的随机数,x(n)表示第n次映射值,lb和ub分别表示下界和上界,min(Ci)和max(Ci)分别表示取当前粒子Ci各维分量的最小值和最大值。式(16)和式(17)表示结合动态边界以后重建的新边界。 如图3所示,该方法通过计算单一粒子在各维度上的边界极值,对称建立新边界以降低维间干扰。改进后的反向学习策略如式(18)所示: Figure 3 Dynamic random boundary(2-dimensional) C_op(i)=(Da(i)+Db(i))-x(n)*C(i,:) (18) 如图4所示,切比雪夫映射值在[0,1]内来回跳跃,实现粒子的自我扰动;其次,据图3可知,通过分解粒子(Ci)各维度信息生成虚拟对称粒子(CS_i),随后利用随机数建立随机边界,以此降低各维度之间的互相干扰。 Figure 4 Chebyshev mapping 综上所述,IOLEONS算法的步骤如下所示: Step1设置初始参数,初始化种群。 Step2计算适应度值并依据式(12)和式(13)计算双曲正切算子,设定平衡池。 Step3依据式(15)计算Chebyshev混沌映射值。 Step4计算粒子之间的欧氏距离,选择邻域内适应度值最高的粒子作为局部领导者粒子。 Step5依据式(14)更新各粒子浓度并依据式(16)和式(17)计算此时种群的动态边界。 Step6依据式(18)计算反向解,并进行越界处理和利用贪婪策略保留较优解。 Step7返回执行步骤5和步骤6,直到达到最大迭代次数,输出最优解,算法终止。 3.5.1 随机优化算法的收敛性准则 本文所提的IOLEONS算法属于随机优化算法,因而可利用概率测度法,根据随机算法的收敛准则进行收敛性分析[9]。 条件1若f(D(z,ξ))≤f(z),ξ∈S,则f(D(z,ξ))≤f(ξ),针对于最小化目标函数f(·),S为约束空间RD的子集,z为子集S中的一点,ξ为随机可行解,该条件假定算法所求新解要优于当前解。 条件2对于S中的任一Borel子集A,若其测度v[A]>0,则: (19) 其中,测度v[A]定义为A的闭包,μt[A]为测度μt[]达到A的概率值,该条件假定连续搜索未寻找到A中点的概率为0。 3.5.2IOLEONS算法的全局收敛性分析 证明由式(14)可得: C(t+1,j)=Y(j)*C(t,j)+(1-Y(j)) Ceq(j)+E(j) (20) E=(G/(λV))(1-F)+(1-r1)* (local_leader_pos(i)-Ceq) (21) 其中,C(t,j)表示(任意)粒子C在第t次迭代时的第j维分量,Y=F*r1,当Ceq和E固定时,式(20)为差分方程,其解如式(22)所示: C(t,j)=k+(C(0,j)-k)*(Y(j)) (22) (23) 其中,k表示衰减常数。 □ 引理1IOLEONS算法满足条件1。 证明在IOLEONS算法中,解序列为{C(t)},Pt为迭代t次时全局最优解,对IOLEONS算法定义函数D(·)为: 由贪婪策略不难看出,改进算法满足条件1。 □ 引理2IOLEONS算法满足条件2。 Mi,t,j=Y(j)*Ci(t,j)+ (1-Y(j))*Ceq(j)+E(j) (24) □ 时间复杂度作为判断算法运行效率高低的一个重要指标,在算法分析中占据重要地位。时间复杂度大小与算法输入端和算法的运算逻辑有密切关系,主要影响因素有种群规模(N)、迭代次数(max_iter)、评估函数值(f)、问题维度(D)。由文献[10]可知EO算法的时间复杂度值如式(25)所示: O(EO)=O(N·D+max_iter·f·N+ max_iter·N+max_iter·N·D)= O(max_iter·f·N+max_iter·N·D) (25) 本文中的IOLEONS算法主要从3个方面改进:首先,利用双曲正切算子改进平衡池中平均浓度值的方法相较于算术平均方法增加的时间复杂度为O(max_iter);改进领域搜索机制增加的时间复杂度为O(max_iter·N);改进反向学习策略增加的复杂度为O(max_iter·N),因此改进算法的综合时间复杂度如式(26)所示: O(IOLEONS)=O(N·D+max_iter·f·N+ max_iter·N+max_iter·N·D)+ O(max_iter+max_iter·N+max_iter·N)= O(max_iter·f·N+max_iter·N·D) (26) 综上所述,IOLEONS算法虽增加了运算量,但是与标准EO算法的时间复杂度保持量级一致。 本文在表1所示的8个基准函数[7]上进行仿真实验,其中,F1~F4为单模态函数,F5~F7为多模态函数,F8为固定维度函数,部分基准函数的详细介绍可参考文献[7]。 Table 1 Benchmark functions 因IOLEONS算法中混合3种策略,其中涉及的参数主要为切比雪夫映射的初始值x(1)及邻域范围值m,因而需要进行独立重复实验设定最优输入参数。设定实验次数为30,维度为30,迭代为500次,模拟出的参数敏感性热力图如图5和图6所示,图中的数值是适应度值(fit)转换后的数值,以方便比较。图中横轴表示x(1)初始值的变化范围,纵轴表示m值的变化范围。经反复实验,发现对于F6和F7外的基准函数,参数的变化对实验结果无明显影响。对于多模态函数F6和F7,由于m值的大小决定了计算邻域范围时的工作量,故取较小m值为宜。因F6和F7函数极为相似,故取两测试函数在同一变量下的均值作为衡量标准。经上述规则界定后,选定m值为5,x(1)为0.3时最优,此时均值(Value)最小,为1.50。 Figure 5 Hotpot of F6 Figure 6 Hotpot of F7 4.2.1 智能优化算法对比 为验证改进算法的效果,本文选取部分优化算法进行对比,其中包括经典优化算法:粒子群优化算法PSO(Particle Swarm Optimization)、鲸鱼优化算法WOA(Whale Optimization Algorithm)[11]、灰狼优化算法GWO(Grey Wolf Optimizer)、标准EO算法及EO算法的改进型(自适应平衡器优化算法AEO(Adaptive Equilibrium Optimizer)[4]和联合均衡优化器算法UEO(United Equilibrium Optimizer)[12])。对比算法的参数设定如表2所示,表中参数的含义参见相应的文献。为避免实验结果的偶发性,进行30次独立重复实验,设定迭代次数为500次,维度为30维,测试平均值(Ave)和标准差(std),实验结果如表3所示,表中每个函数对应2行数字,第1行数字表示测试平均值,第2行数字表示标准差。 Table 2 Parameter settings Table 3 Benchmark test results of intelligent optimization algorithms 4.2.2 其他改进智能优化算法对比 为进一步验证IOLEONS算法的性能优势,选取近几年来的改进智能优化算法进行对比:具有速度辅助全局搜索机制的增强型灰狼优化器VAGWO(Velocity-Aided Grey Wolf Optimizer)[13]、半参数自适应混合CMA-ES的LSHADE算法(LSHADE-SPACMA)[14]、精英反向学习的黄金正弦鲸鱼优化算法EGolden-SWOA(Elite opposition-based Golden-Sine Whale Optimization Algorithm)[7]、利用自适应策略的改进型粒子群算法MPSO(Modified PSO using adaptive strategy)[15]、双适配粒子群算法DFPSO(Dual Fitness Particle Swarm Optimizer)[16]、多选择反向灰狼优化算法SOGWO(Selective Opposition based Grey Wolf Optimization)[17]、融合螺旋策略的分片混沌振荡搜索算法DCSOA-S(Divided Chaotic Swarm Oscillation Algorithm merged with Spiral strategy)[18]。对比算法的参数设定如表2所示。依旧采用上述测试集进行同等次数独立重复实验,结果如表4所示。 Table 4 Benchmark test results of improved algorithms 图7~图14是IOLEONS算法与对比算法的收敛曲线图。 Figure 7 Convergence curves of F1 using intelligent optimization algorithms 从表3中可看出,IOLEONS算法在单模态测试函数上均取得最优的平均值和标准差,这表明改进EO算法具有优越的局部开发能力,并且由图7和图8的收敛图可以看出,IOLEONS算法的收敛速度更快、精度更高,这是因为双曲正切算子在迭代过程中的自适应变化与算法全程优化的一般规律相吻合,提高了算法在前期的收敛速度;通过在多模态基准函数F5~F7上的运行结果不难看出,改进算法具有较好的稳定性和较高的收敛精度,并且从图9的收敛曲线可看出,在迭代过程中,改进算法的收敛速度更快、精度更高,这是因为对于多模态基准函数来讲,邻域机制的引入降低了算法在优化全过程中陷入局部最优解的风险,并且由于动态对称反向学习机制的引入,进一步改善了在迭代后期种群多样性差的局面;对于固定维度的测试结果依旧领先于其他算法,证明了IOLEONS算法的优越性。 Figure 8 Convergence curves of F3 using intelligent optimization algorithms Figure 9 Convergence curves of F6 using intelligent optimization algorithms Figure 10 Convergence curves of F8 using intelligent optimization algorithms 从表4中可看出,与其他改进智能优化算法相比,IOLEONS算法在单模态、多模态和固定维度函数上均有不俗的表现,从图11~图14的收敛图也可以看出,IOLEONS算法收敛速度更快,进一步展示了改进算法的优势。 Figure 11 Convergence curves of F1 using improved intelligent optimization algorithms Figure 12 Convergence curves of F3 using improved intelligent optimization algorithms Figure 13 Convergence curves of F6 using improved intelligent optimization algorithms Figure 14 Convergence curves of F8 using improved intelligent optimization algorithms 为验证多算子混合改进策略的有效性,本节将各算子逐步添加到标准EO算法中,并各自在30维基准函数上进行30次独立重复实验,设定迭代次数为500次。将EO算法融合双曲正切算子后的算法定义为EO_1算法;将EO算法融合双曲正切算子和添加邻域搜索机制的算法定义为EO_2算法,测试结果如表5所示。 Table 5 Test results on benchmark functions 由表5可知,对于EO_1算法,在单模态基准函数F1~F4上的收敛精度和稳定性均有很大幅度的提升,证明了EO_1算法的局部开发能力有了较大的提升,但是从F6和F7多模态基准函数来看,其性能反而下降,说明在增强局部开发能力的同时破坏了开发和探索之间的平衡,降低了算法的探索功能;从EO_2的运行结果来看,在基本保持单模态基准函数精度不变的情况之下,F6函数的稳定性和精度有了极大的改善,但是从F7的结果来看,探索能力仍需进一步加强。IOLEONS算法通过动态对称反向学习策略的加入,进一步增强了算法的全局探索能力,并且在单模态基准函数之上更是取得了理论最优解,进一步证明了混合策略融合的有效性。 仅依靠均值和标准差值就判断算法性能优劣的做法不能充分利用全体数据,为了深入比较算法之间的差异,需用一定的统计假设进行检验。为此本文选取Wilcoxon秩和检验和Friedman秩检验对30次实验结果进行验证,设定显著性水平均为5%。当检验结果p值低于5%时,便认为2种算法之间存在显著差异;反之,则认为2个样本数据(算法运行结果)在统计学上无显著差异。各对比算法与IOLEONS算法之间的计算结果如表6所示,数值为1则认为两者数据完全相同。表7中最后2行数据则为秩检验中不同算法的秩均值排名,其中IOLEONS算法得分最小,展现了算法的优越性。 Table 6 Results of Wilcoxon signed rank test Table 7 Results of Friedman rank test 结合表3和表4可知,表6中所示72个数值中仅有2处数值高于5%,且未达到理论最优值;另有2处数值为1且均达到理论最优值。结合表3认为IOLEONS算法与对比算法在寻优性能上有显著差异且改进算法寻优性能有较大提升。 压力容器设计问题PVD(Pressure Vessel Design)[19]作为一种经典的工程优化问题,其优化的主要目标是降低所设计容器带来的生产成本,涉及头部半径(R1)、柱体长度(L)、罐体厚度(Ts)和封头厚度(Th)4种变量,如图15所示,其数学模型如式(27)所示: Figure 15 PVD sketch map s.t. -x1+0.0193x3≤0, -x2+0.00954x3≤0, (27) 为验证IOLEONS算法在PVD问题上的表现,本文选取EO算法作为基准对比算法,并对比PSO、AEO算法与本文改进算法EO_1、EO_2算法,设置IOLEONS算法的实验参数为k1=0(对应EO_1),k2=1(对应EO_2),其余参数不变,并进行30次独立重复实验,实验结果如表8所示,对应的收敛迭代图如图16所示。 Table 8 Comparison results of PVD Figure 16 Convergence curve of IOLEONS for solving PVD 从表8中可以看出,对比算法之间均取得相同的最优解,但是在均值和标准差方面表现不一,其中以IOLEONS算法的性能表现最佳。并且从图10的收敛曲线可以看出,改进算法具有更快的收敛速度,进一步表明改进算法在优化PVD工程问题上具有卓越性能优势。 本文针对EO算法的不足从多方面进行改进:利用双曲正切算子修改平衡池以匹配算法进化过程;其次引入邻域机制提高算法的局部开发能力;针对算法后期种群分散度差的局面,利用动态对称和映射的技巧来改进反向学习策略。对于收敛特性,本文用理论对改进算法的收敛性进行了证明,并用实验结果验证了改进算法的优越寻优性。最后利用工程算例进一步表明了改进算法在现实中的应用价值。下一步,将继续对EO算法进行改进,充分挖掘标准EO算法的优势。3 改进策略
3.1 双曲正切自适应算子
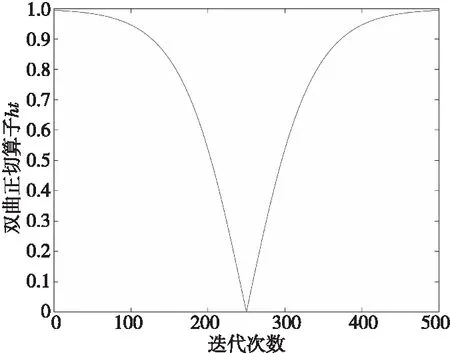
3.2 邻域搜索机制
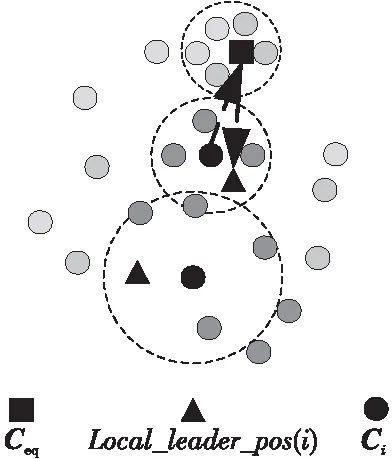
3.3 动态对称反向学习
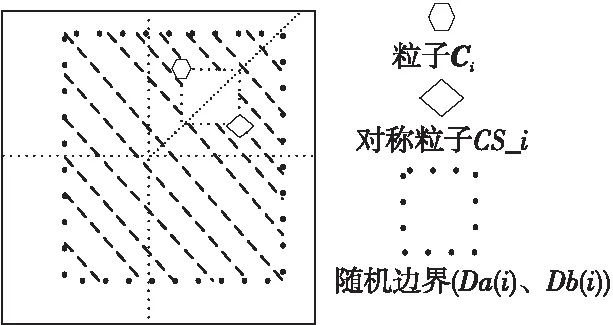
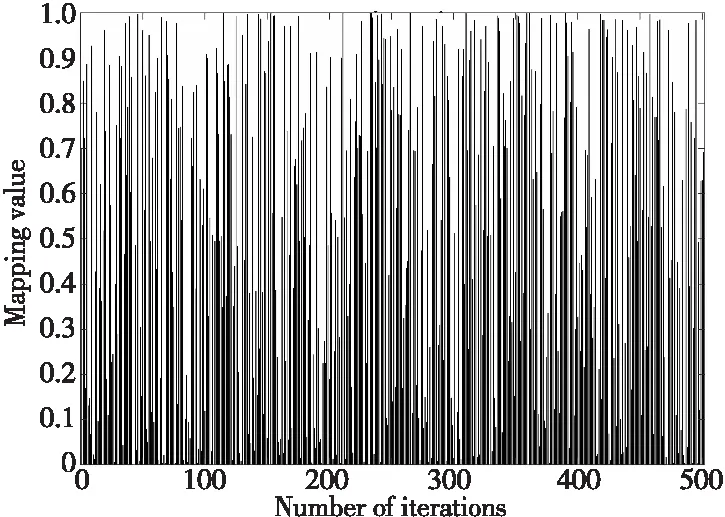
3.4 IOLEONS算法流程
3.5 收敛性分析
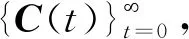
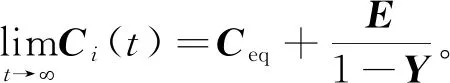
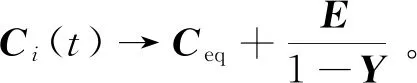
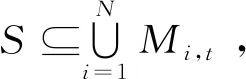
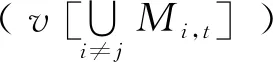
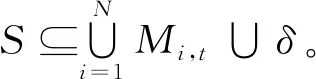
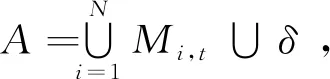

3.6 时间复杂度分析
4 实验结果与数据分析
4.1 基准函数与算法参数敏感性分析
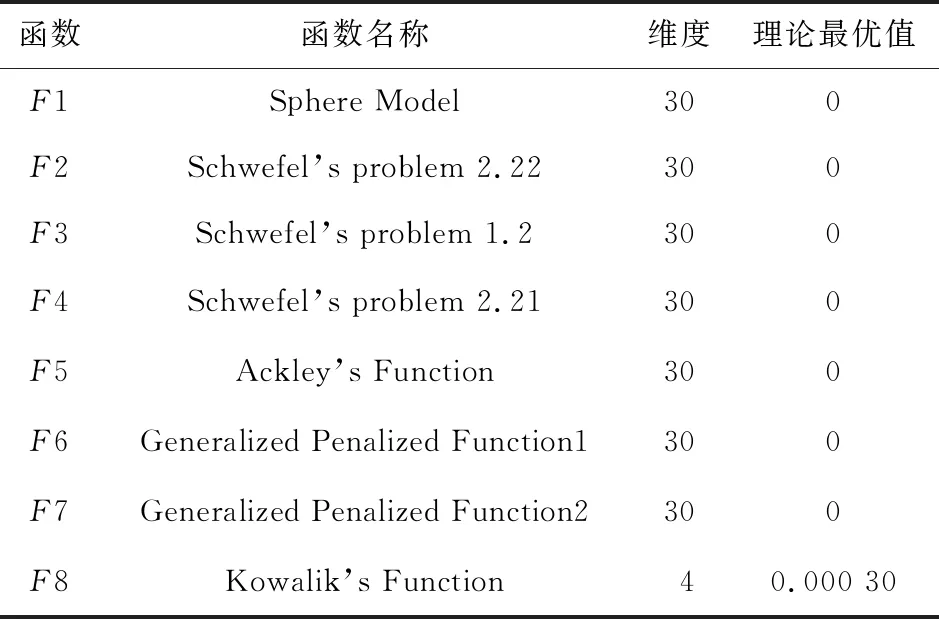
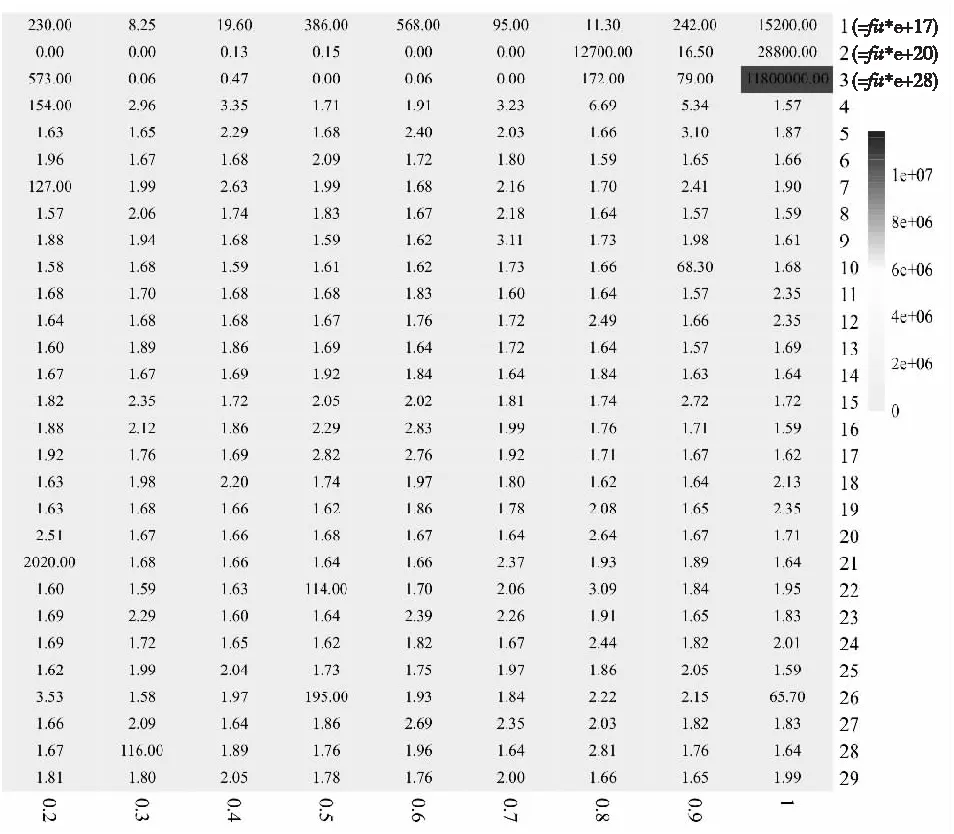
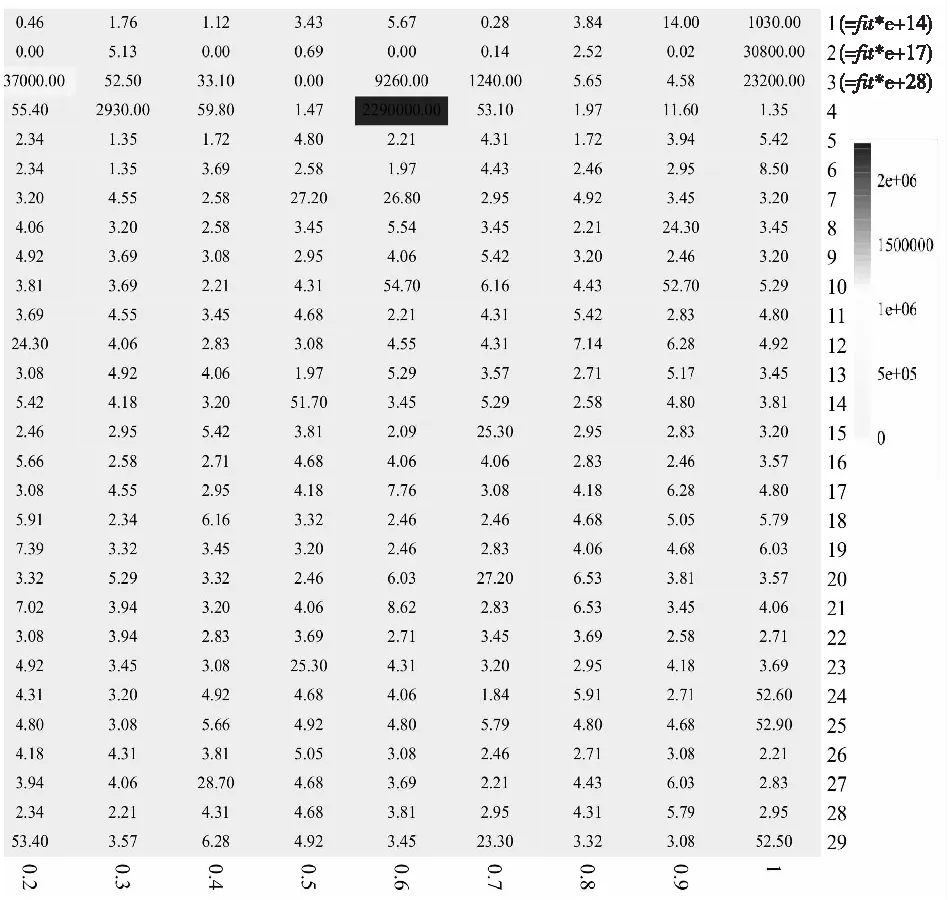
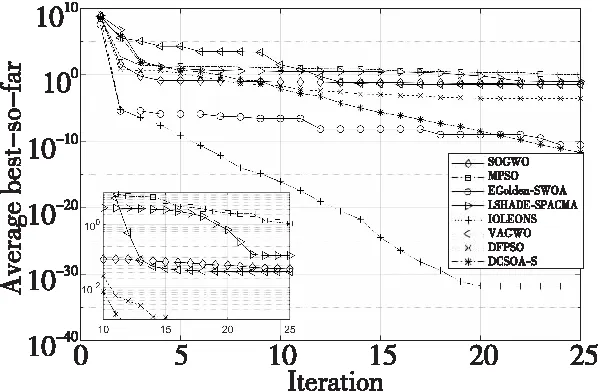
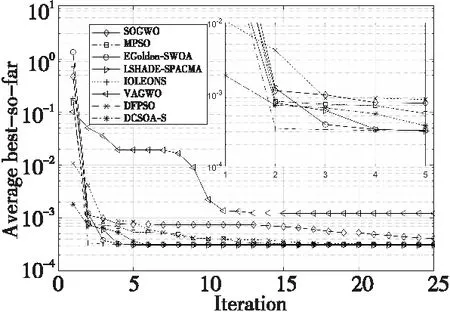
4.2 算法对比分析

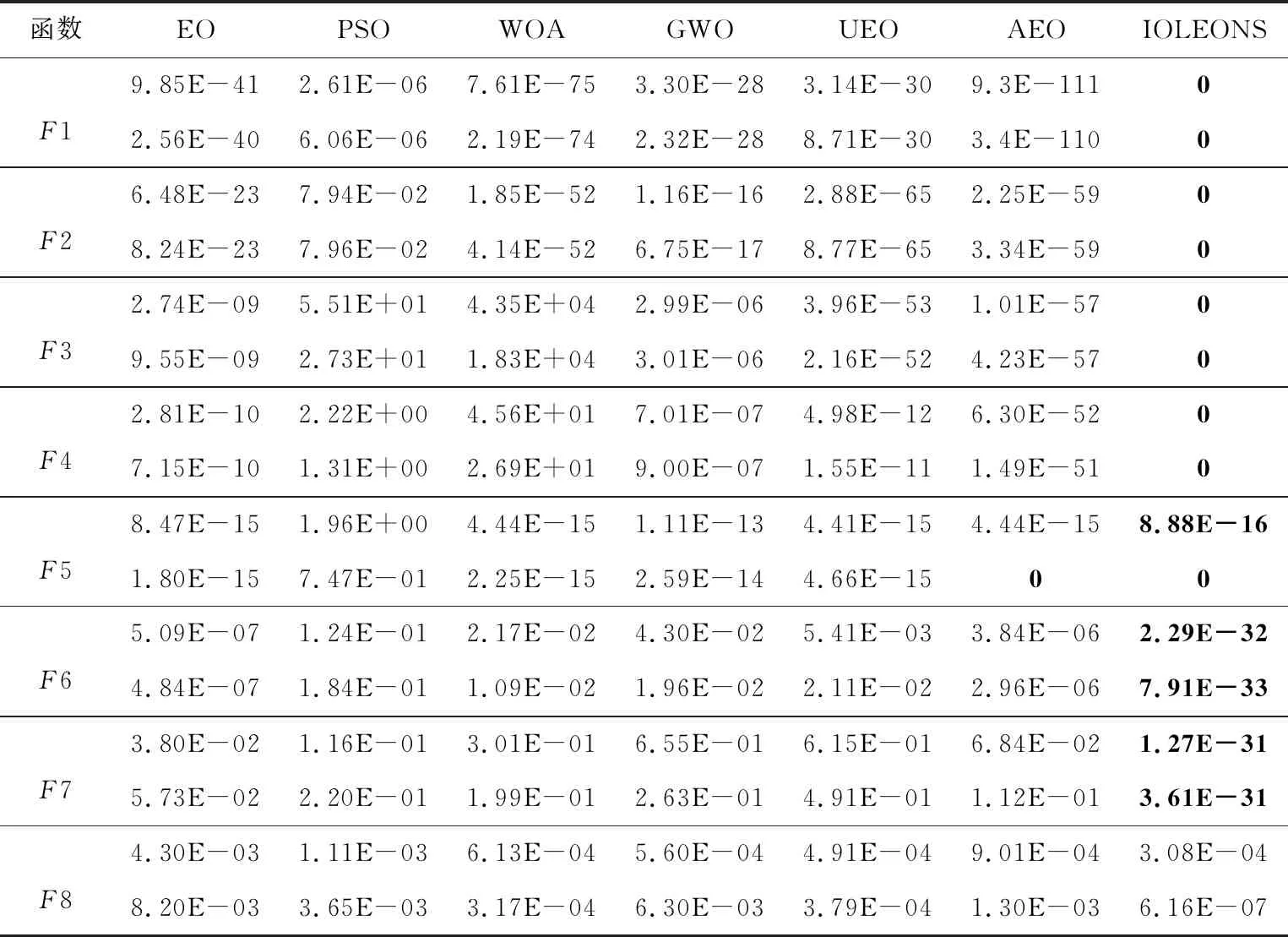
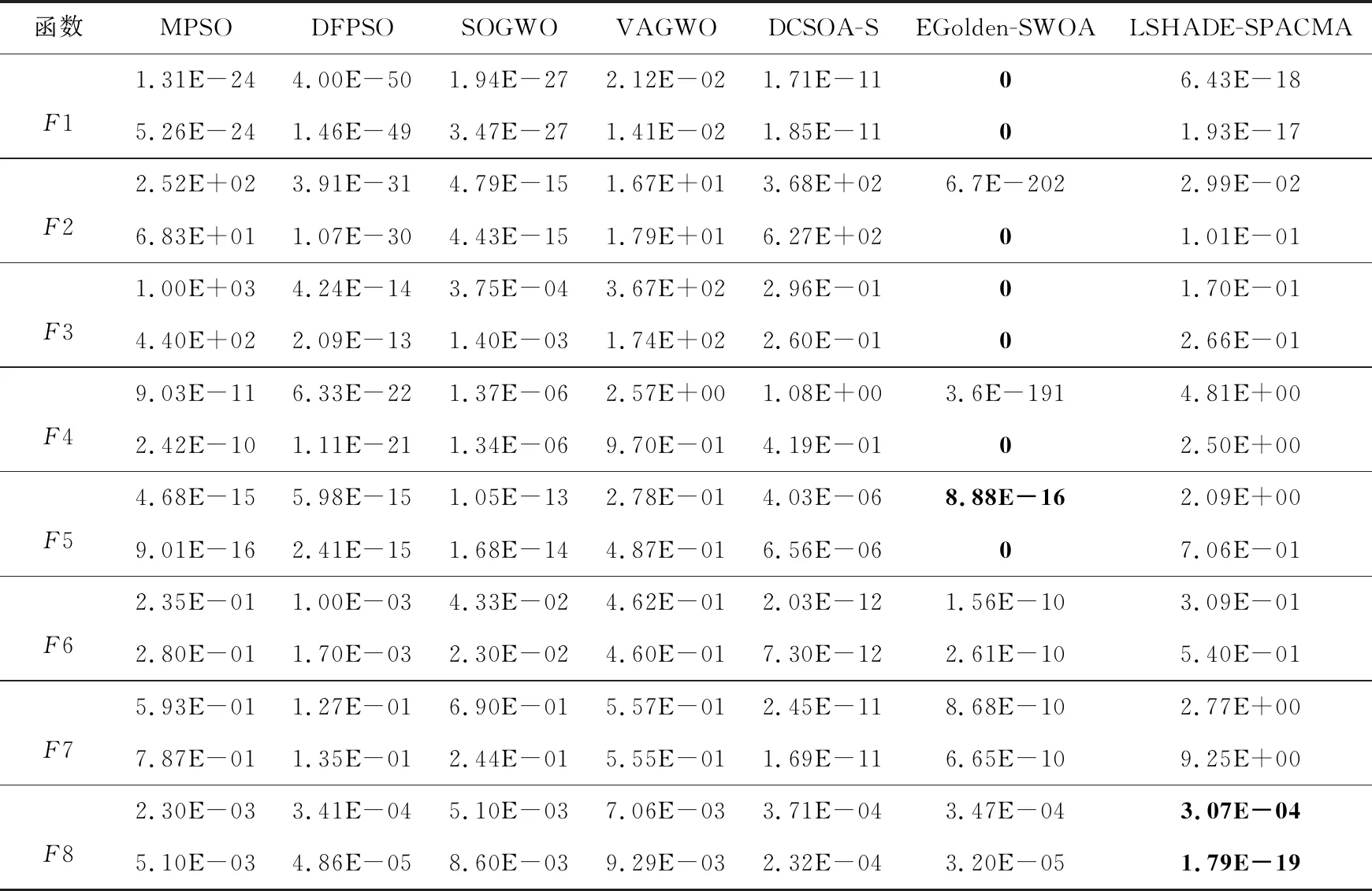
4.3 基准函数测试分析


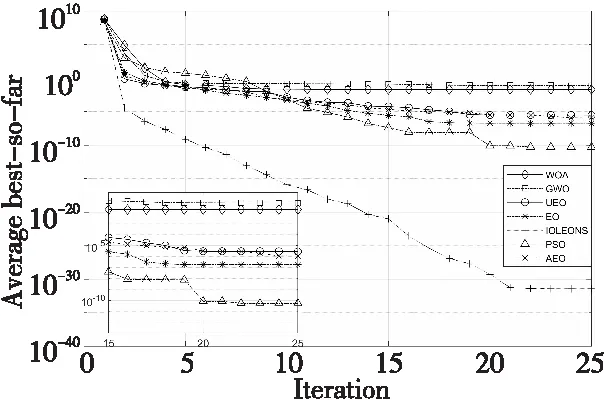
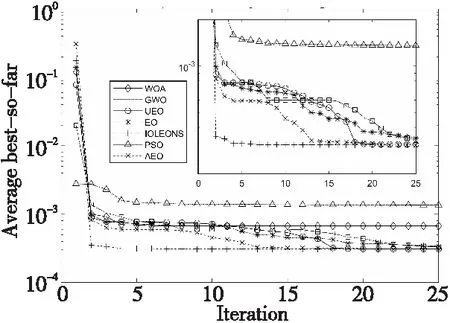
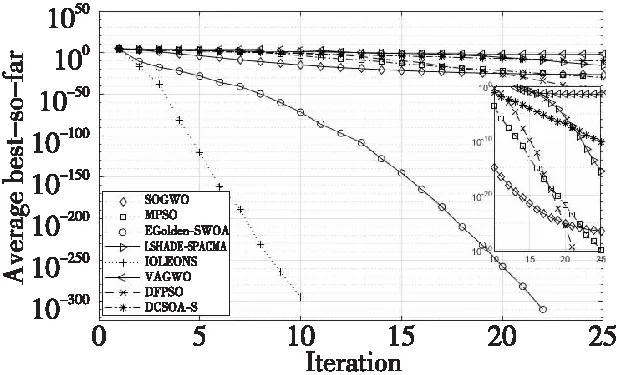
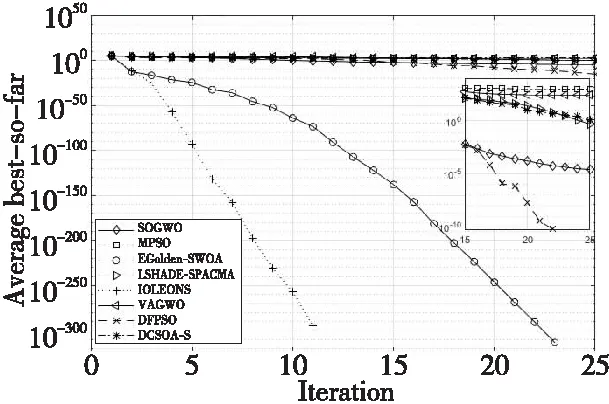
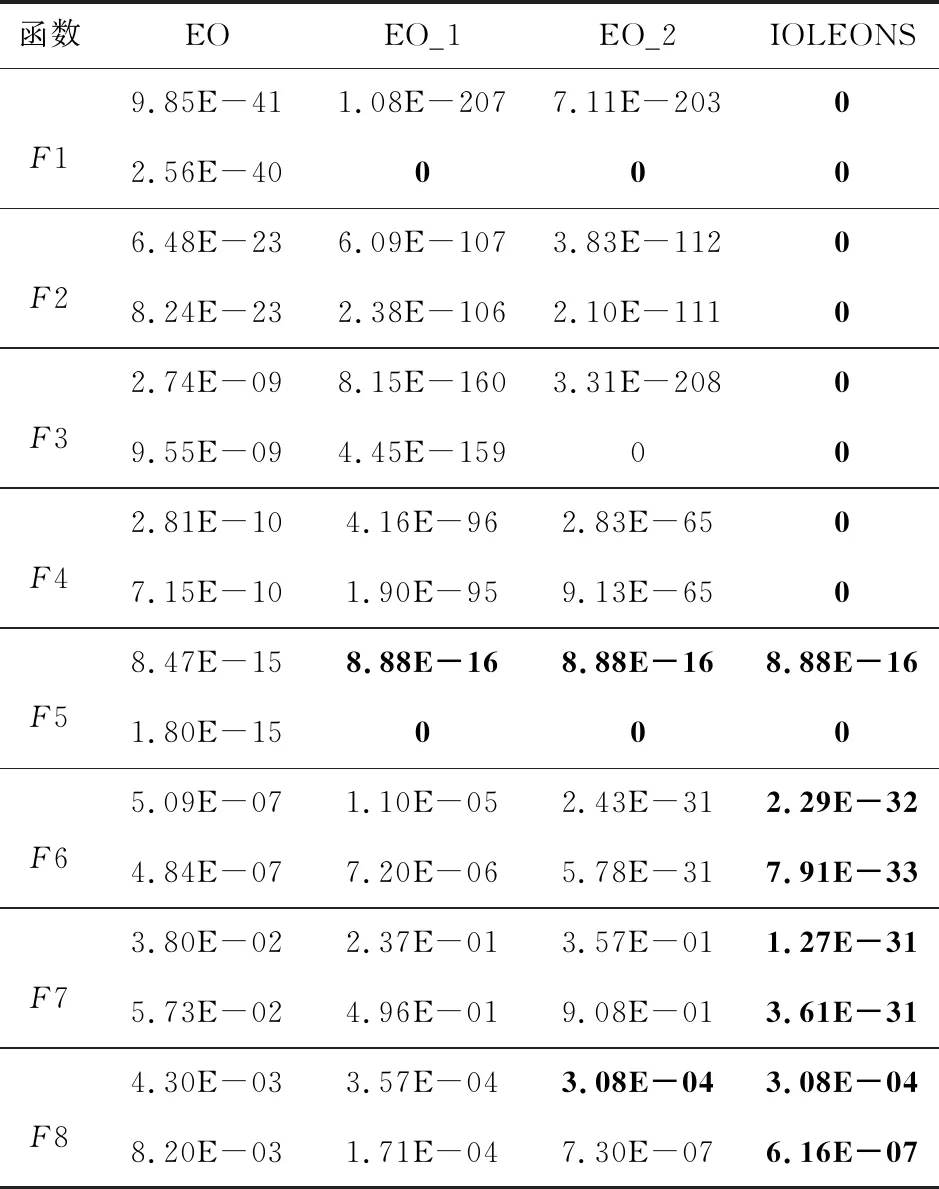
4.4 算子贡献度分析
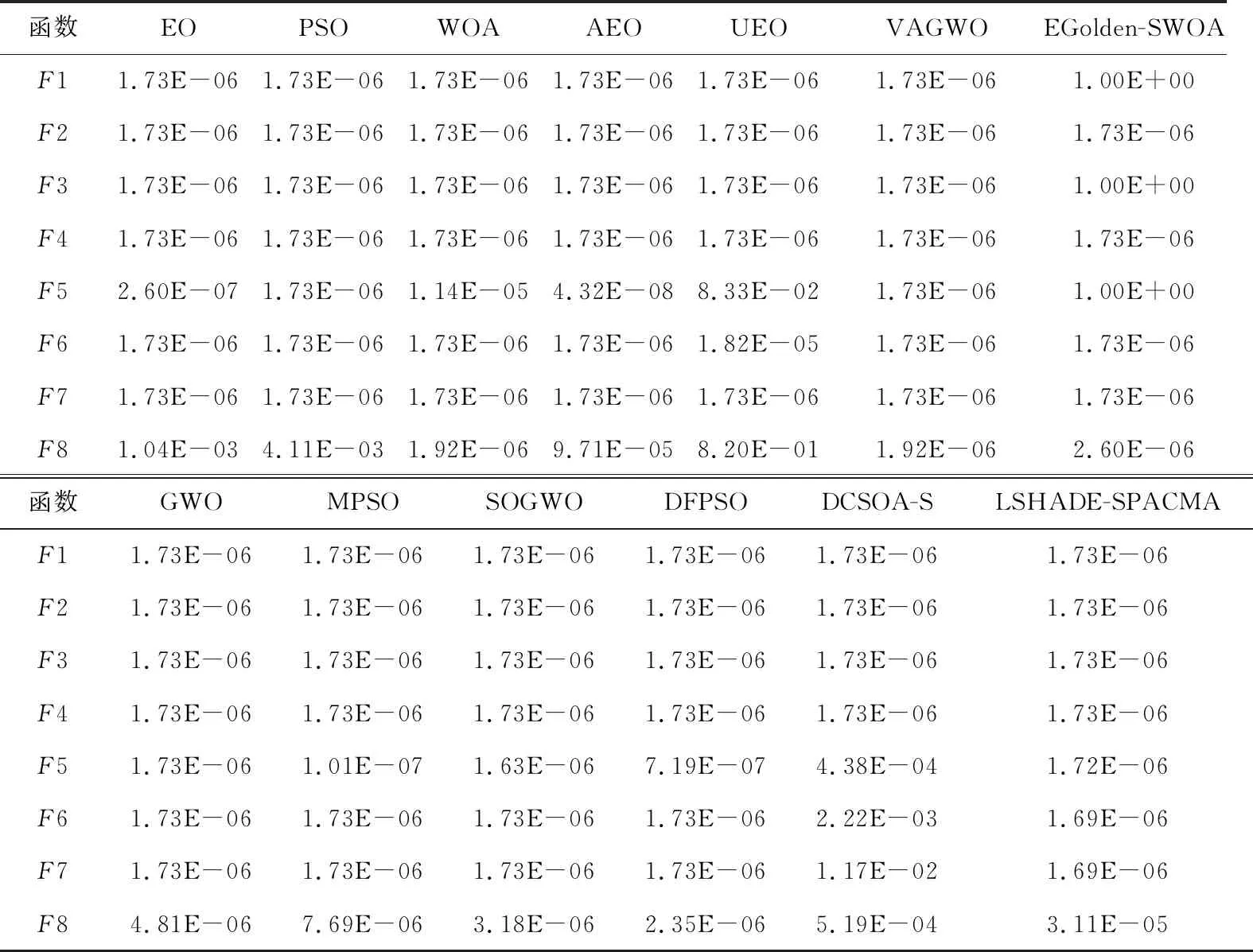
4.5 统计学检验

5 工程优化案例分析
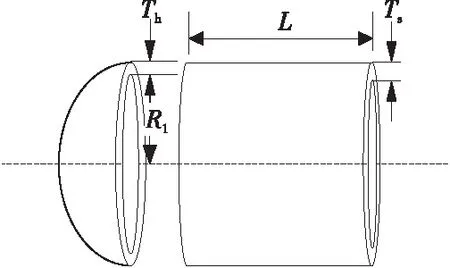
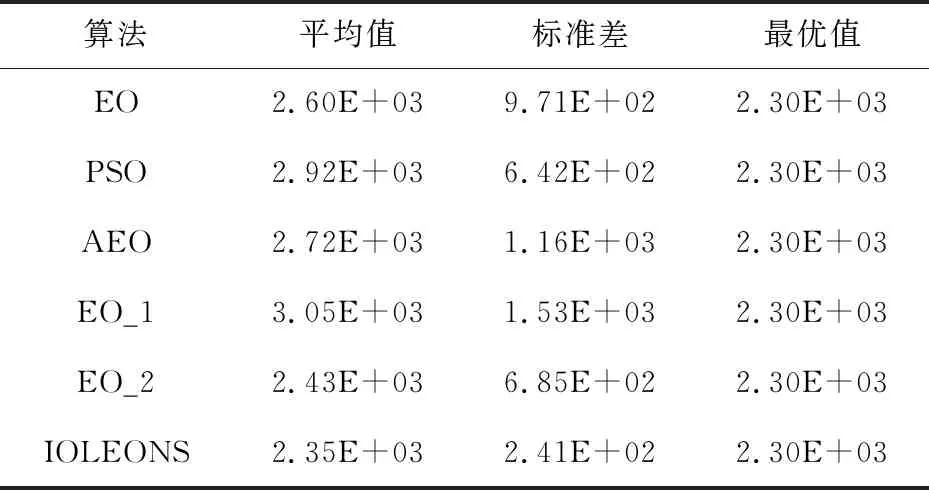
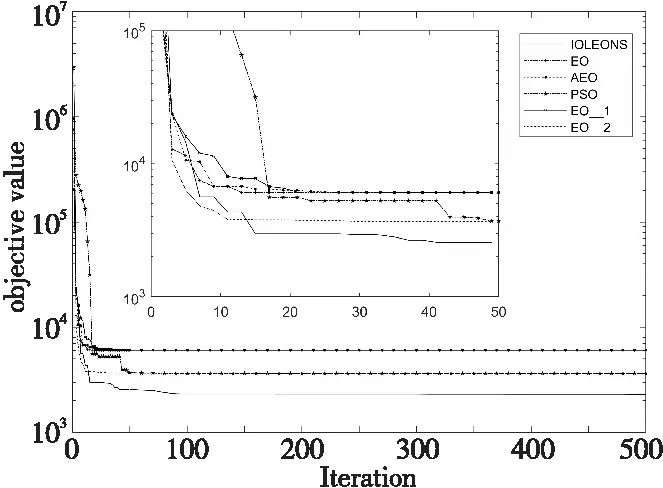
6 结束语
