基于FPGA的2底指数函数算法优化与实现

2023-09-18程甜甜宋宇鲲

电子科技 2023年9期

程甜甜,宋宇鲲

(合肥工业大学微电子学院,安徽合肥 230601)

指数函数是一种常见的超越函数,广泛应用于数字信号处理、人工智能、控制系统和导航系统等领域,也是实现多种超越函数例如Power函数xy的重要中间函数[1-3],其在信号滤波[4]和雷达通讯[5]中也具有重要应用。芯片工艺制程的快速发展给超越函数的硬件实现提供了基础。相比于软件计算,硬件电路具有运算速度快、并行度高以及实时性好等优势。常见的指数函数硬件实现算法都是计算欧拉数e的指数函数,即y=ex,但是以2为底的指数函数y=2x在图像处理、信号滤波、飞行器控制等工程领域中也具有广泛应用[6-7]。本文研究一种高精度、高性能的2x的实现电路。

常用的指数函数的硬件实现方法有查找表法(Look Up Table,LUT)、坐标旋转数字机(Coordinated Rotation Digital Computer,CORDIC)算法和多项式近似法等。查找表法将函数值存在表中,根据输入数据直接读取表中对应的函数值,其延时低且适用于任何底数的指数函数,但随精度的增加,存储资源以2的幂次方增加[8]。CORDIC算法通过不断的角度偏摆以逼近目标角度,硬件只有移位和加法运算,但提高精度需要增加迭代次数,计算延迟、高实时响应特性不好且计算范围较窄[9-12]。多项式近似法是将指数函数近似为多项式计算[13-15]。受收敛域限制,多项式法的计算难以覆盖整个定义域,若要提高精度和计算范围,只能增加多项式的项数或者分段处理。前者会增加硬件计算资源[16],而后者需要折中选择分段和项数[17]。

针对上述方法存在的问题,本文设计了一种基于改进的查找表与泰勒级数展开相结合的指数函数硬件计算电路。利用区间划分的预处理方法对输入数据进行压缩,所需中间数据提前计算存于表中,然后利用泰勒级数展开式计算指数函。相较于文献[2～3],本文设计的电路资源消耗更少,输入值范围更宽,精度更高。

1 优化算法说明

泰勒级数展开式法是把目标函数通过泰勒展开成多项式求和形式来实现逼近目标函数解[18]。此为基础,本文将2x转换为ex的形式后通过泰勒展开计算,所用的泰勒展开式为

(1)

为满足数据吞吐量,要求泰勒展开式多采用流水线全展开结构实现。泰勒级数展开式法的精度与展开项数成正比,高精度要求意味着更多的乘法器和加法器。文献[3]表明在泰勒展开式中x<0.125,指数函数的泰勒展开式取5项,即展开至x4项,能够保证计算精度在10-7量级。本文设计了输入变量x的预处理操作,将输入数据压缩至较小的收敛区间,利用查找表存储中间计算数据,实现用最少的泰勒展开项数满足预期精度要求。优化后的算法流程如图1所示,具体预处理步骤如下所示:

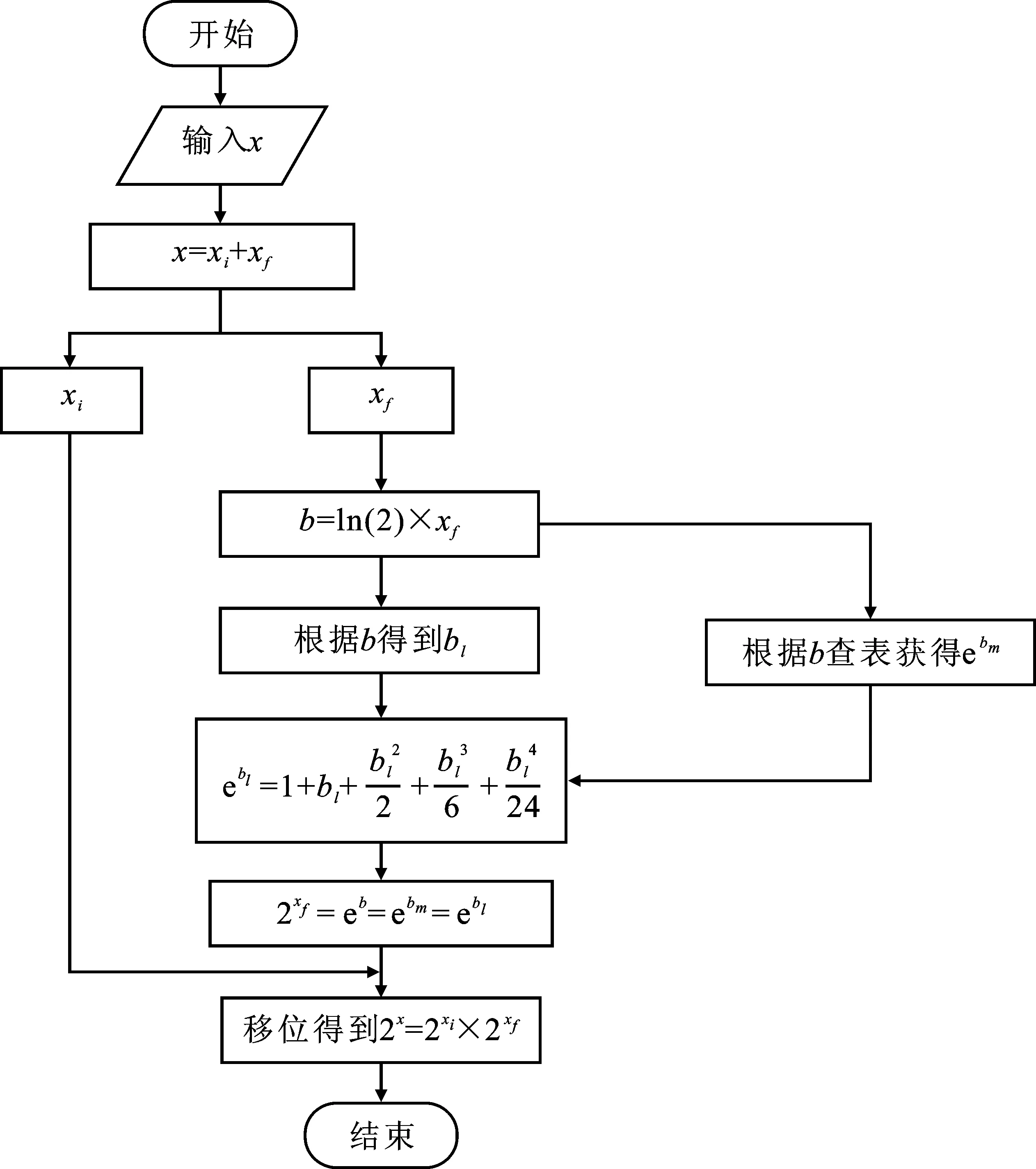
图1 优化算法流程Figure 1. Flow of optimization algorithm

步骤1令x=xi+xf,xi和xf分别为x的整数部分和小数部分,对于整数部分的指数值2xi的计算通过移位逻辑即可实现,因此将设计重点放在小数部分的指数函数值2xf的计算上。令b=xf×ln(2),则2xf=eb,将2xf通过换底变为eb。

步骤2eb用泰勒级数展开式求解,b的范围为(-0.693 15,0.693 15),直接计算所需项数仍较多。为进一步缩小代入展开式计算的数据范围,对b继续拆分。令b=bm+bl,bm是b的高m位,其数值为bm=round(b×2m)/2m。其中,round(·)表示四舍五入函数,bl是b除去高m位剩余的低位部分,eb公式变形为eb=ebm×ebl。这种拆分方法将[-1,1]的区间等分成2×2m份,控制bl在(-1/2m,1/2m)范围内,计算时ebm固定在查找表中,通过b的高m位寻址获得。上述操作将eb的计算转换成ebl的计算,实现输入数据的压缩。

步骤3利用e指数函数的泰勒展开式计算ebl。

(2)

展开式的项数由划分的区间大小及所需的精度要求决定。综上步骤,指数函数2x的求解计算式变换如下所示。

2x=2xi+xf=2xi×2xf=2xi×ewf×ln(2)=2xi×ebm×ebl

(3)

2 硬件实现

2.1 参数选择

区间划分程度和展开式项数影响存储资源和精度。在理论上,对b的拆分区间划分越细,实现相同精度下所需展开式的项数越少,对指数函数的近似精度越高。但过细的区间划分会导致高存储问题,因此需要权衡存储和计算资源与精度的关系。

为选择硬件实现的合适参数,对优化算法进行高级语言建模以分析参数与性能的对照关系,如表1所示。其中,N表示泰勒级数式(2)的展开项数,m表示区间划分参数,表1中的数据为计算指数函数的最大相对误差量级,存储资源消耗为64×2m。

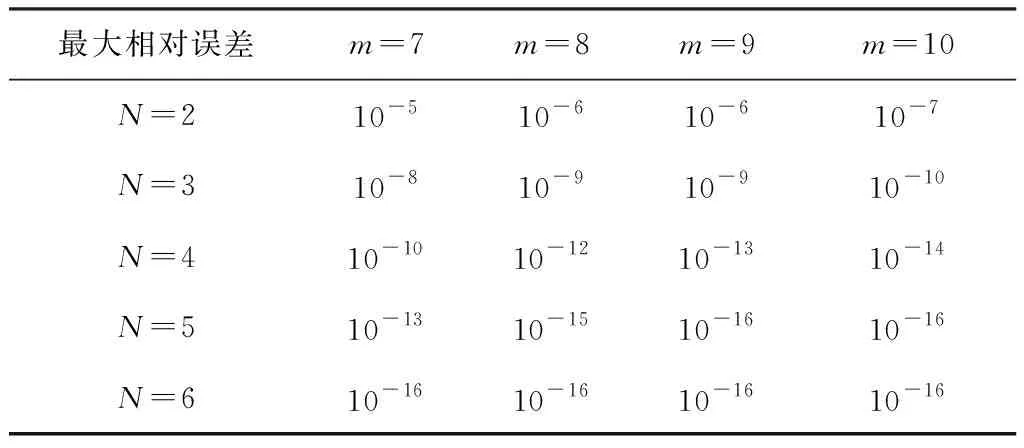
表1 不同参数组合下的最大相对误差Table 1. Maximum relative errors under different combinations of parameters

如表1所示,当固定区间划分参数m=9时,bl的范围为(-1/512,1/512)。对比不同展开式项数结果如下:当展开式取5项时,最大相对误差量级刚好为10-16,再增加展开式项数,误差不变;减少展开式项数,每减少1项,最大相对误差增大3～4个数量级。双精度浮点数在十进制下的有效数字为15～16位,相对误差为10-16能够满足双精度的精度要求。

当固定展开式取5项时,展开式为

(4)

对比不同的区间划分参数m,结果表明,当m=9时最大相对误差量级刚好为10-16;当m≤8时误差增大,不能满足双精度浮点数的精度要求;当m>9时增大m精度不再提高。因此在双精度的数据格式下,区间划分的参数m=9、展开式项数N=5最为合适。

单精度浮点数的有效数字为6～7位。从表1可以看出,当m=7、泰勒级数展开式取3项时,优化算法的最大相对误差量级刚好能达到10-8,满足单精度浮点数的精度要求,此时bl的范围为 (-1/128,1/128),泰勒展开式如式(5)所示。

(5)

2.2 精度评估

根据上述算法描述和参数选择,从理论角度给出精度评估。泰勒计算式为

(6)

其中,Rn(x)表示余项,表示一个从A(x-x0)n+1开始直至无穷多项的多项式,Rn(x)可表示精度,余项越小,精度越高。Rn(x)取拉格朗日余项,计算式为

(7)

其中,ξ是x的取值范围[a,b]的一个跟x有关的点,此处取ξ为[a,b]上使f(n+1)(x)取最大值的点。

在双精度计算下,指数函数的泰勒级数展开至x4项,为

(8)

(9)

计算可得指数泰勒计算的最大误差为2.373 1×10-16。按照双精度浮点数尾数52位,则双精度浮点数的表示精度为2-52≈2.220 4×10-16,因此改进算法的最大误差满足双精度浮点数的精度要求。

同理,在单精度计算下,展开式展开至x2项,数据范围为(-1/128,1/128),则n=2,ξ=1/128。按照上述计算方法可得优化算法的最大误差为8.009 6×10-8,单精度浮点数的表示精度为2-23≈1.192 1×10-7,同样满足单精度浮点数的精度要求。

2.3 硬件结构

优化算法的硬件实现结构如图2所示,主要分为拆分电路、查表电路、泰勒展开求解电路3部分电路实现。

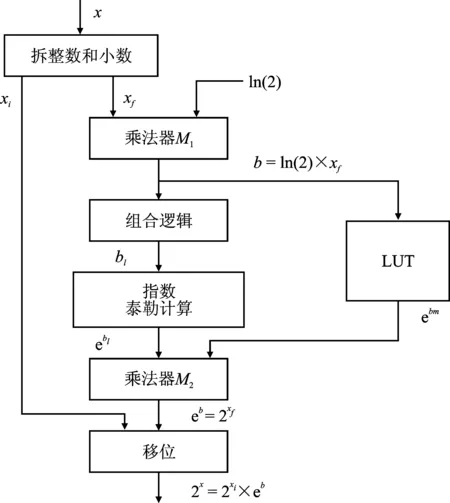
图2 优化算法的硬件实现结构Figure 2. The hardware implementation structure of the optimized algorithms

将输入的浮点形式的x通过组合逻辑拆分成整数和小数,为不丢失精度,拆分后的数据以伪浮点的形式存储,采用11位寄存器记录小数点的位置,另用53位寄存器记录有效数据。图2中乘法器M1为53位定点乘法器,直接用小数部分xf的有效位与53位常数ln(2)相乘,得到106位的定点数b。待其余电路计算完后对结果进行整数部分xi的移位。

为压缩存储资源,在读取查找表中的ebm时,可以用两级逼近的方法代替直接存储以节省一半的资源。两级逼近的方法原理如图3(a)和图3(b)所示,分别为向左逼近和向右逼近。根据优化算法的参数选择可知,区间划分参数m=9,b=bm+bl。通过b的高9位判断b的范围,根据图3中举例可知,两种情况下b的范围均为(3/256,4/256)。图3(a)中的b更接近左端点3/256,拆分时令bm=3/256,bl=bm-b。图3(b)中的b更接近右端点4/256,则令bm=4/256,bl=b-bm,此时bl为负数。

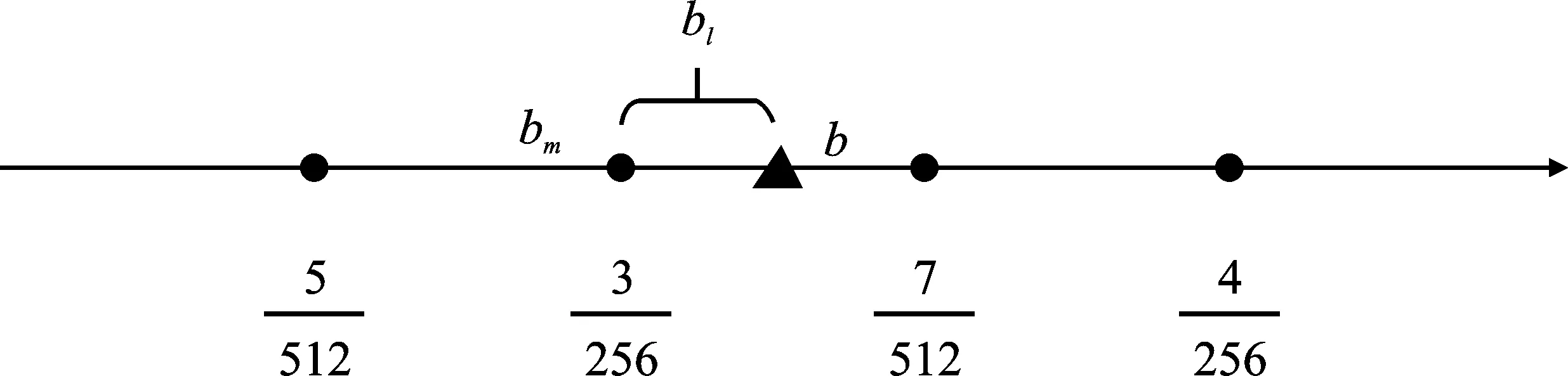
(a)

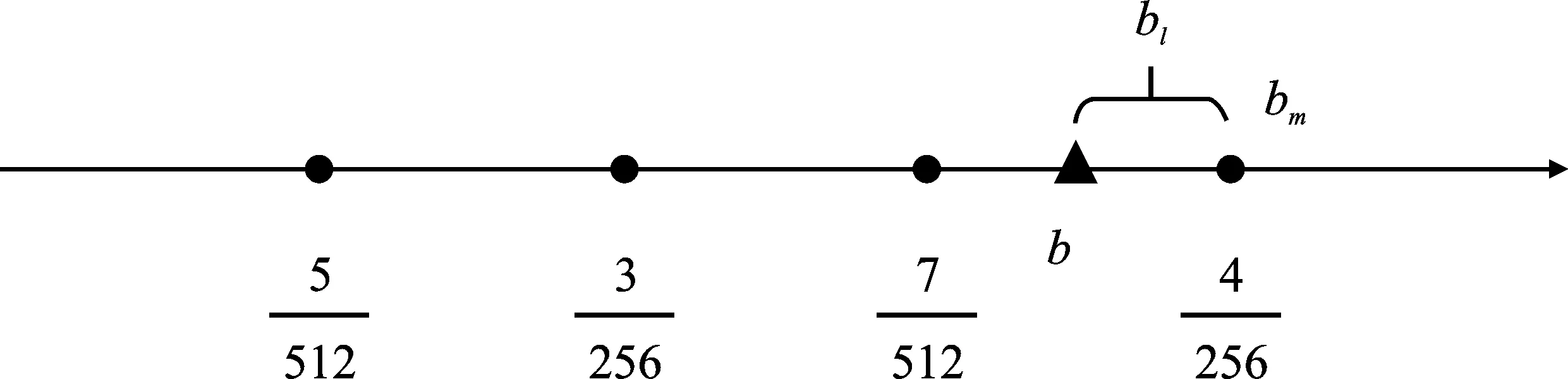
(b)图3 两级逼近方法(a)向左逼近 (b)向右逼近Figure3. The two-stage approximation method(a)Near to the left (b)Near to the rirgt

若采用直接存储方法,[-1,1]的区间被等分为1 024等份,需要存每一个区间端点处的指数函数值ebm,其硬件信号名为exp_bm,如下所示:

共需存储1 024个数据,此时查找表大小为1 024×64 bit,10位地址线为b的符号和b的高9位b[105:97]的组合。

[2]教育部.普通高等学校.校数［EB/OL］.http://www.Moe.edu.cn/publicfiles/business/htmlfiles/moe/s4960/－201012/113594.html

若采用两级逼近的方法,则在只读存储器(Read Only Memory,ROM)中按如下方式存放数据:

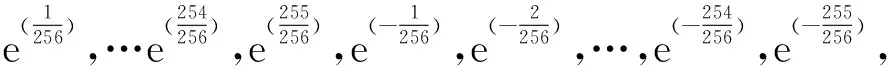
在得到ebm的同时,根据b确定bl。bl是范围在(-1/512,1/512)之间的数,因此bl的高8位为0,根据两级逼近原理,bl的其余有效位根据b[97:0]确定。如图4所示,其中向右逼近的情况会出现减法,此时取数据的补码。bl的符号根据b的符号和b[97]共同决定,当b[97]=0时,bl与b同号,反之异号。

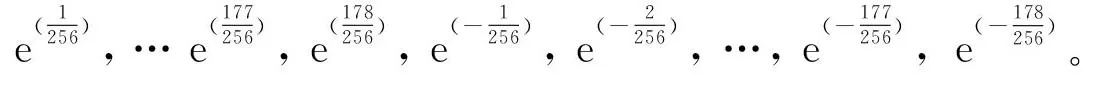
图5所示为式(4)的硬件实现电路,式(4)中的常系数乘法除1/3外,均可通过移位逻辑实现,降低了乘法操作次数。考虑到流水结构和资源之间的权衡,展开式由5个乘法器和3个加法器实现,通过4级计算得到。

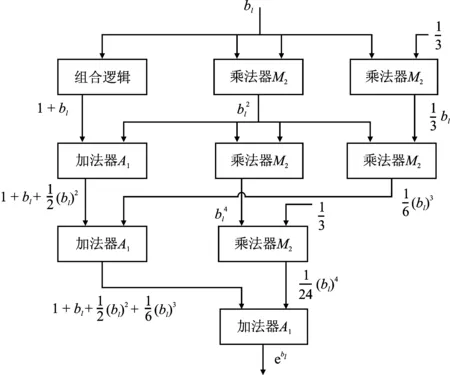
图5 指数函数的泰勒级数展开电路Figure 5. Taylor series expands circuit of exponential function

图5中由bl得到1+bl的组合逻辑,展开如图6所示。由106位的定点形式的bl,直接转换为64位的双精度浮点形式的1+bl。根据bl的符号位作为多路选择器的判断位,补全1+bl的11位阶码,根据bl的数值确定1+bl的尾数。

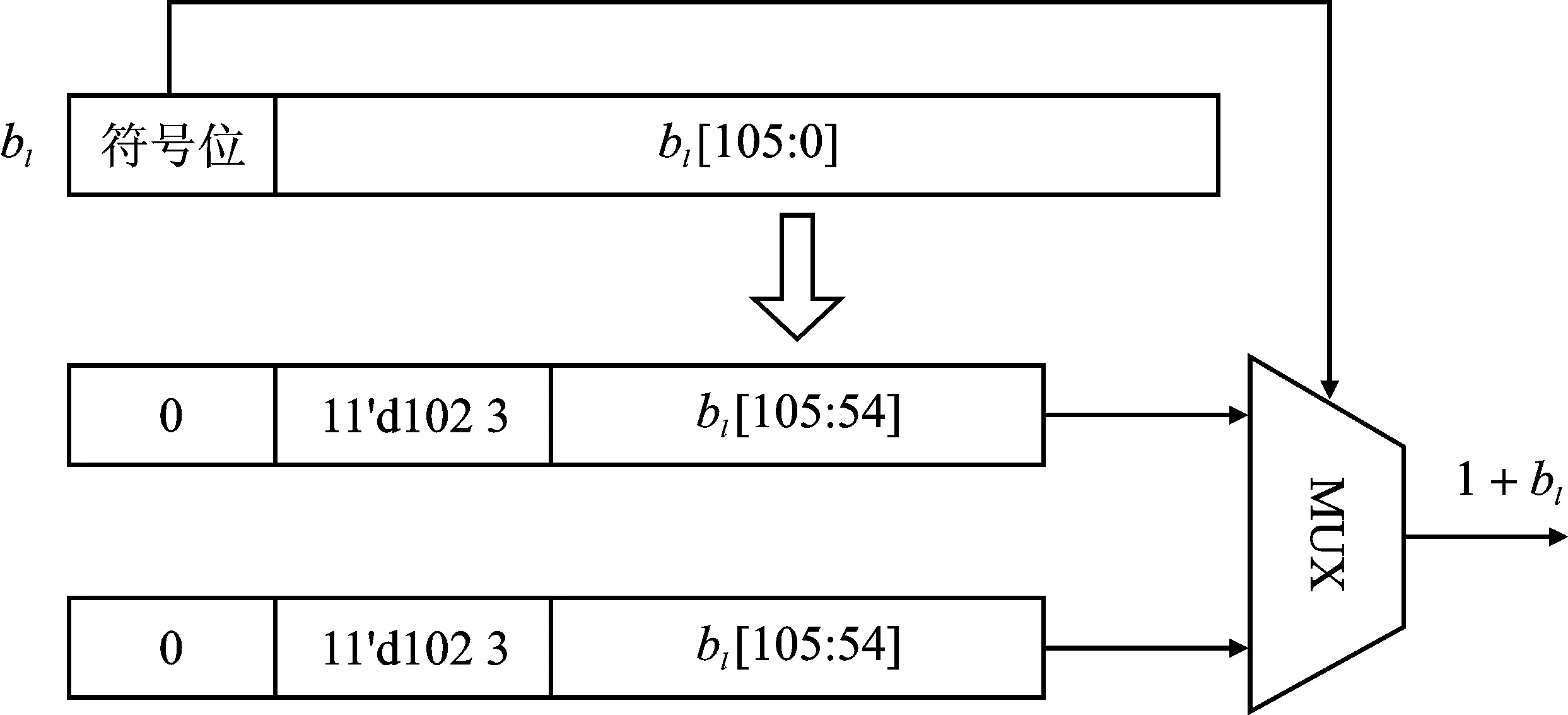
图6 1+bl计算电路Figure 6. Calculating circuit of 1+bl

3 实验结果与分析

本文设计的指数函数计算单元,利用Verilog HDL硬件描述语言进行编程,使用Vivado 2018.3在Xilinx公司XC7K325T现场可编程门阵列(FPGA)芯片完成优化算法的硬件实现,并对算法的精度、速度、资源消耗以及适用范围等性能进行评估。

在双精度浮点数数值格式下,计算范围为(-1 024,1 024),超出范围将导致结果溢出,整个计算过程采用流水线结构,频率为185 MHz,最大相对误差量级为10-16。表2为系统资源使用情况。

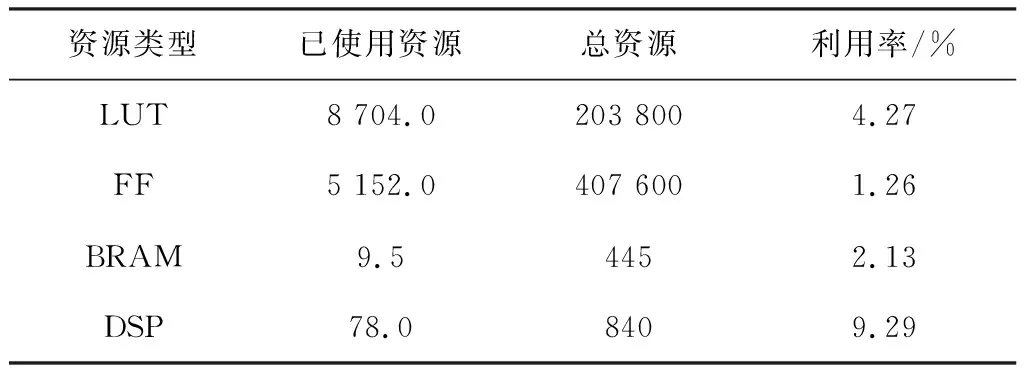
表2 系统资源使用情况Table 2. The utilization of system resources

实验测试数据利用MATLAB工具中的unifrnd(·)函数随机生成若干组一维数据,通过网口下发到FPGA开发板中,然后将硬件计算结果通过网口回传到电脑端,与MATLAB计算的数据进行比较分析。在双精度范围下,指数的样本范围为[-1,1]、[-10,10]、[-100,100]、[-1 023,1 023]这4组,每组选取10 000个随机测试样本,将硬件电路计算值与MATLAB中指数函数计算结果进行对比,对比结果如表3和图7所示。

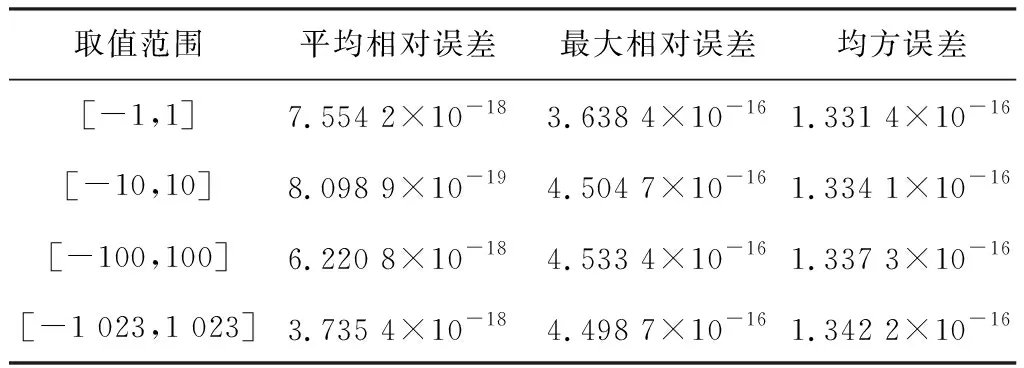
表3 不同定义域内电路的计算误差Table 3. Calculation errors of circuits in different definition domains

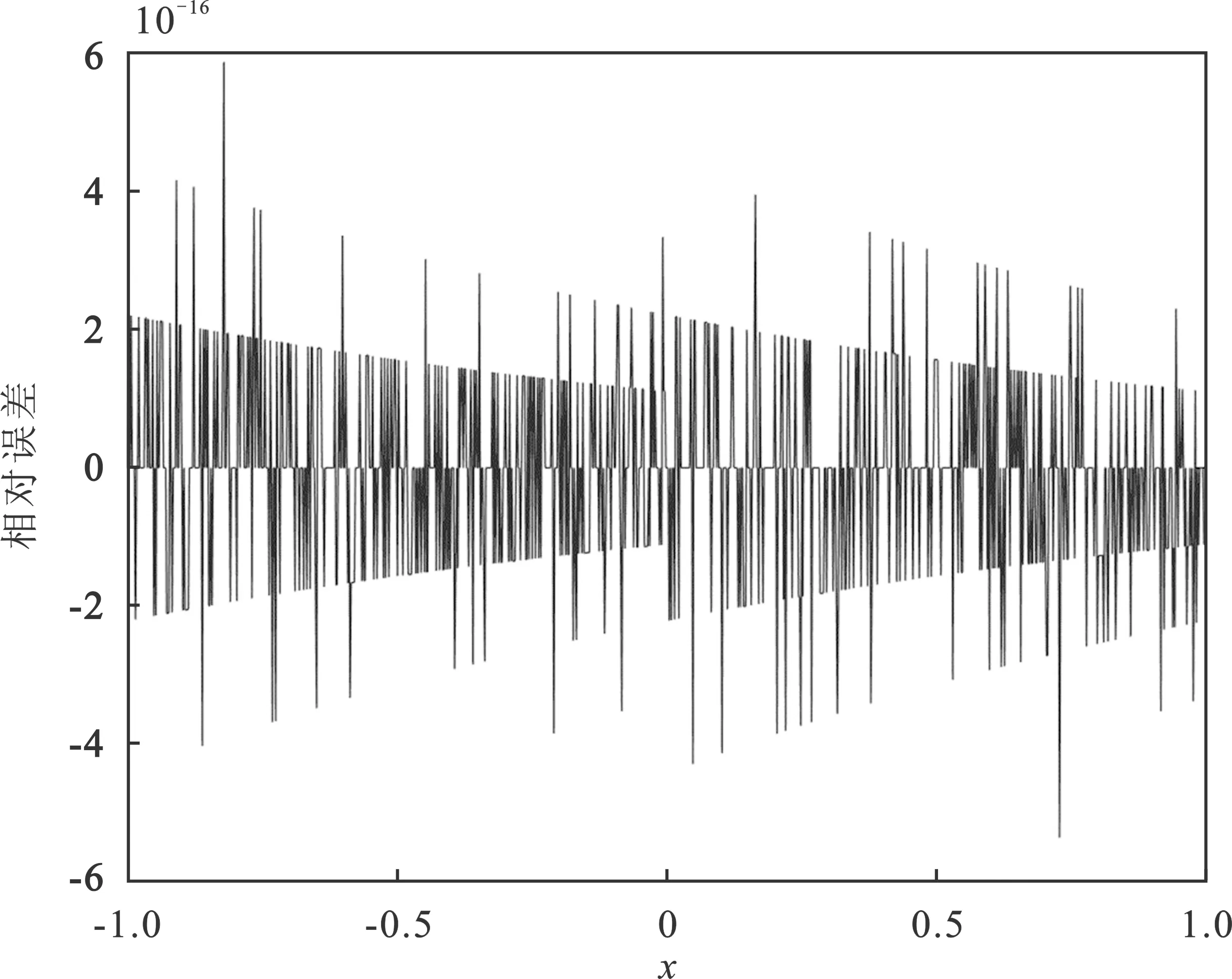
(a)

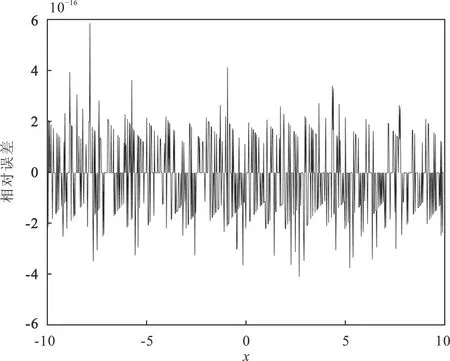
(b)

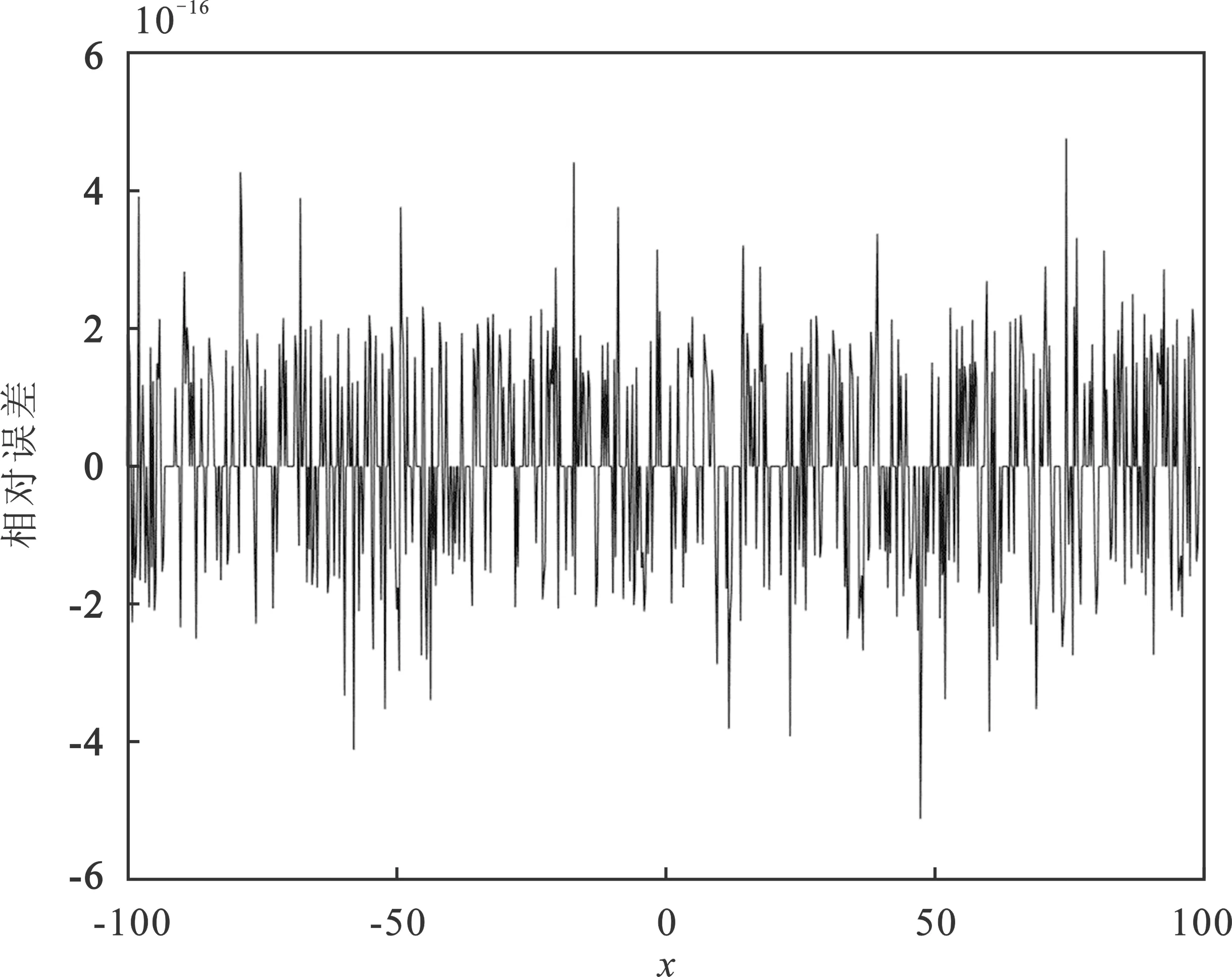
(c)

根据表3和图7可知,指数函数在所有计算范围内误差稳定,最大相对误差量级为10-16,平均相对误差量级为10-18,均方差为10-16。这表明,本文设计的指数函数硬件计算电路可以保证在全部定义域范围内保持较高的计算精度。

表4为本文电路结构与文献[2]和文献[3]提出的电路结构分别进行性能比较的结果。由于文献[3]是在单精度浮点数的范围下计算,因此将本文电路结构相关参数映射到32位单精度浮点数的计算范围下与之进行对比。

表4 性能对比Table 4. Performance comparison

文献[2]采用CORDIC实现128位四精度浮点数的指数函数计算,采用67级流水结构,在(-8 192,528)范围内可保证10-6以上的精度,电路结构面积小、功耗低,而本文结构中两种精度下的计算均可超过文献[2]的精度。由于文献[2]采用ASIC工艺,其他参数与本文设计不具有可比性,暂不予比较。

文献[3]实现的是e指数函数ex,本文所提方法和电路是实现2x。但二者在核心计算部分均采用的e指数的泰勒级数展开式,且拆分方法具有相似性,且本文在实现2x时也是通过转换成ex来求解,因此具有可比性。

文献[3]也采用泰勒公式与查找表相结合的方法,在进行泰勒公式计算前对输入的x进行处理。由于处理部分算法原理不同,文献[3]计算的数据范围较大,需要的泰勒级数展开式项数更多。在单精度的计算范围下,文献[3]需要展开至x4项,即

(10)

而本文电路只需要展开至x2项,即

(11)

优化算法在双精度实现时需展开至x4项,与文献[3]在单精度下展开项数一致。展开式的项数影响硬件计算资源的消耗,展开项数越多,加法器和乘法器越多、硬件面积越大、计算延迟更高。文献[3]的设计在Microsemi公司LGLOO2系列的M2GL150 FPGA上实现,本文结构的存储资源在单精度下比文献[3]少55.6%,而定义域范围均为整个单精度浮点数,两者计算精度几乎一致,在单精度下均为10-7。根据两者综合结果,本文所提方法在硬件实现指数函数时,优势较明显。