Level density of odd-A nuclei at saddle point

Wei Zhang · Wei Gao · Gui-Tao Zhang · Zhi-Yuan Li

Abstract Based on the covariant density functional theory, by employing the core-quasiparticle coupling (CQC) model, the nuclear level density of odd-A nuclei at the saddle point is achieved.The total level density is calculated via the convolution of the intrinsic level density and the collective level density.The intrinsic level densities are obtained in the finite-temperature covariant density functional theory, which takes into account the nuclear deformation and pairing self-consistently.For saddle points on the free energy surface in the (β2,γ) plane, the entropy and the associated intrinsic level density are compared with those of the global minima.By introducing a quasiparticle to the two neighboring even-even core nuclei, whose properties are determined by the five-dimensional collective Hamiltonian model, the collective levels of the odd-A nuclei are obtained via the CQC model.The total level densities of the 234-240 U agree well with the available experimental data and Hilaire’s result.Furthermore, the ratio of the total level densities at the saddle points to those at the global minima and the ratio of the total level densities to the intrinsic level densities are discussed separately.

Keywords Level density · Covariant density functional theory · Core-quasiparticle coupling model · Saddle point

1 Introduction

As a fundamental nuclear property, nuclear level density(NLD) plays a crucial role in many applications, such as the calculation of reaction cross sections with nucleosynthesis,the nuclear reaction calculation program TALYS [1], and the Hauser-Feshbach model for compound nucleus calculations [2, 3].Owing to the complexity of nucleon interactions and the fact that the level density increases exponentially with an increase in the excitation energy, the accurate calculation of the NLD has long been a theoretical challenge.Many methods for estimating NLD have been developed.The most common method is the Bethe formula based on the zero-order approximation of the partition function of the Fermi gas model [4, 5].In attempting to reproduce the experimental data, various phenomenological modifications to Bethe’s original analytical formulation have been proposed-particularly to account for shell, pairing, and deformation effects-which led first to the constant-temperature formulation, then to the shifted Fermi gas model, and later to the popular back-shifted Fermi gas model [2, 6, 7].

There are many microscopic methods for calculating NLD, including the shell-model Monte Carlo method[8-10], the moments method derived from random matrix theory and statistical spectroscopy [11, 12], the stochastic estimation method [13], the Lanczos method using realistic nuclear Hamiltonians [14], the self-consistent mean-field approach based on the extended Thomas-Fermi approximation with Skyrme forces [15], and the exact pairing plus independent-particle model at a finite temperature [16-19].On the basis of the Hartree-Fock-Bogoliubov (HFB) model,S.Hilaire and S.Goriely developed a microscopic approach to describe NLD with great success [20-22].Microscopic methods based on the self-consistent Hartree-Fock (HF)plus BCS model [23-25] have also been developed.

Recently, on the basis of the relativistic Hartree-Bogoliubov model [26-29], Zhao et al.developed a method for describing NLD [30].In this model, the partition function is determined using the same two-body interaction employed in the HF plus BCS and HFB mean-field models [25],which includes shell, pairing, and deformation effects of self-consistently.The total level densities are the convolution of the intrinsic level density and the collective level density.The intrinsic level density is obtained by an inverse Laplace transform of the partition function with the saddlepoint approximation [31, 32].Previously, the collective enhancement is considered via a phenomenological or semiempirical multiplicative factor for rotational and vibrational degrees of freedom [24, 33-36] or more microscopically via a combinatorial method using single-particle level schemes obtained through HF plus BCS or HFB calculations [20, 22].In Ref.[30], the collective enhancement is determined from the eigenstates of a corresponding collective Hamiltonian that considers quadrupole or octupole degrees of freedom.Both the intrinsic level density and the collective enhancement are determined by the same global energy density functional and pairing interaction.

The success of the microscopic description of NLD in even-even nuclei prompts us to extend it to odd-Anuclei.The core-quasiparticle coupling (CQC) model introduces a quasiparticle to the neighboring even-even core nuclei within the same covariant density functionals and achieved progress for describing the quantum phase transition in odd-Anuclei.It is based on the covariant density functional theory (CDFT), which has achieved considerable success in describing ground-state properties of both spherical and deformed nuclei all over the nuclear chart [26,27, 37-40].Its successful applications include superheavy nuclei [41-45], pseudospin symmetry [40, 46, 47], singleparticle resonances [48-50], hypernuclei [51-56], thermal shape transition [57-59], and shell correction [60-64].

In this study, the CQC model is applied to the calculation of collective levels in even-odd uranium isotopes.For even-even isotopes, the collective levels are attained via the five-dimensional collective Hamiltonian (5DCH)model [65].Similar to Ref.[30], the intrinsic level density is obtained using the finite-temperature CDFT [58, 59,66].Because the level density of the saddle point plays an important role in the compound nuclei reactions [67, 68],the level density of the saddle pointρsdand the level density of the global minimaρminare analyzed.The ratio of the level density at the saddle point to the level density at the global minimum is the quantity of interest.

The remainder of this paper is organized as follows.The theoretical framework is introduced in Sect.2.The results for234-240U are presented in Sect.3.Section 4 presents a short summary.

2 Theoretical framework

With the assumption of decoupling between intrinsic and collective degrees of freedom, the excitation energy of a nucleus can be written asE*=Ei+Ec, whereEcrepresents the collective excitation energy.The total level density is obtained as [36]

whereSrepresents the entropy, andDis the determinant of a 3×3 matrix that contains the second derivatives of the entropy with respect to the inverse temperatureβ=1∕(kBT)andμN=βλN,μZ=βλZat the saddle point.The intrinsic excitation energy is calculated asEi(T)=E(T)-E(0) ,whereE(T) represents the binding energy of the nucleus at temperatureT.The specific heat is defined by the relation

Cv=∂Ei(T)∕∂T.

According to the ideas presented in Ref.[32], the determinantDcan be simplified to the following form:

whereNandZrepresent the numbers of neutrons and protons, respectively, andλN(λZ) denotes the neutron (proton) Fermi surface.For convenience, the temperature used iskBT(in units of MeV), and the entropy used isS∕kB(dimensionless).

Entropy is extracted in the finite-temperature covariant density functional theory.In the covariant density functional theory, the Dirac equation for single nucleons is

wheremrepresents the nucleon mass, andψk(r) denotes the Dirac spinor field of a nucleon.The scalarS(r) and vector potentialVμ(r) are

For even-even nuclei, the collective levels are obtained via the five-dimensional collective Hamiltonian (5DCH) [65].All the collective parameters, such as the inertia parameters and the collective potential, are extracted from the constrained CDFT+BCS in the triaxial deformation space.

For odd-Anuclei, the collective levels are calculated using the CQC model [69], whose collective Hamiltonian is expressed as

whereλdenotes the Fermi surface, andεA±1andEA±1represent the single-particle energy and the collective excitation energy for the even-evenA±1 core, respectively.Γ and Δ denote the mean and pairing fields associated with longrange quadruple-quadruple particle-hole interactions and short-range monopole particle-particle interactions between the odd nucleon and core, respectively.The Γ field can be expressed as

In this study, the 5DCH and CQC models are based on the CDFT calculation with the harmonic oscillator basisNF=16.

3 Results and discussion

The parameter sets of covariant density functional theory used in this study are PC-PK1 [70] and DD-LZ1 [71].PC-PK1 is one of the most widely used point-coupling parameter sets, and DD-LZ1 is a density-dependent parameter set that aims to alleviate the spurious shell closure.The pairing effect is considered by the separable pairing force [72].The nuclei considered are even-even234-240U and even-odd235-239U.

In the first step, large-scale finite-temperature CDFT calculations are performed for234-240U in the temperature range of 0-2 MeV in the (β2,γ) plane.Figure 1 shows the free energy surface evolution with respect to the temperature for235U.The deformations of the global minimum and the saddle point change slightly with an increase in the temperature, i.e., with the increase in the temperature, the global minimum deformationβ2decreases, while the saddle point deformationγslowly moves toward the prolate axis(γ=0°) andβ2remains nearly constant.The saddle point gradually becomes indistinct as the temperature approaches 1.6 MeV.The free energy surface evolution for other nuclei234,236-240U is similar to that for235U.For the parameter set DD-LZ1, the energy surface shapes are similar, while the fission barrier heights are larger.Moreover, the free energy surfaces of234-240U considering the axial octupole deformations are checked, and it is found that although the PESs of some nuclei are relatively soft in the octupole direction,there is no significant octupole deformation for the global minimum and first saddle point.Therefore, in the following calculation, the deformation space is limited to the (β2,γ)space.

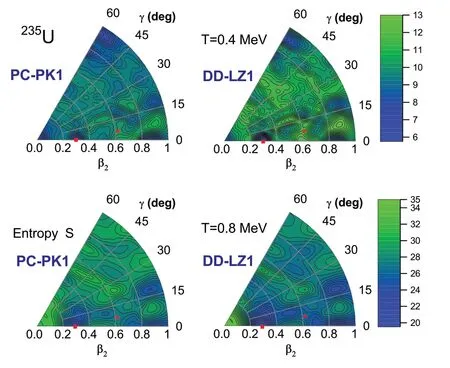
Fig.2 (Color online) Entropy S for 235 U at T = 0.4 MeV (upper row)and 0.8 MeV (lower row) obtained via CDFT calculations using the parameter sets PC-PK1 (left) and DD-LZ1 (right) in the ( β2,γ ) plane

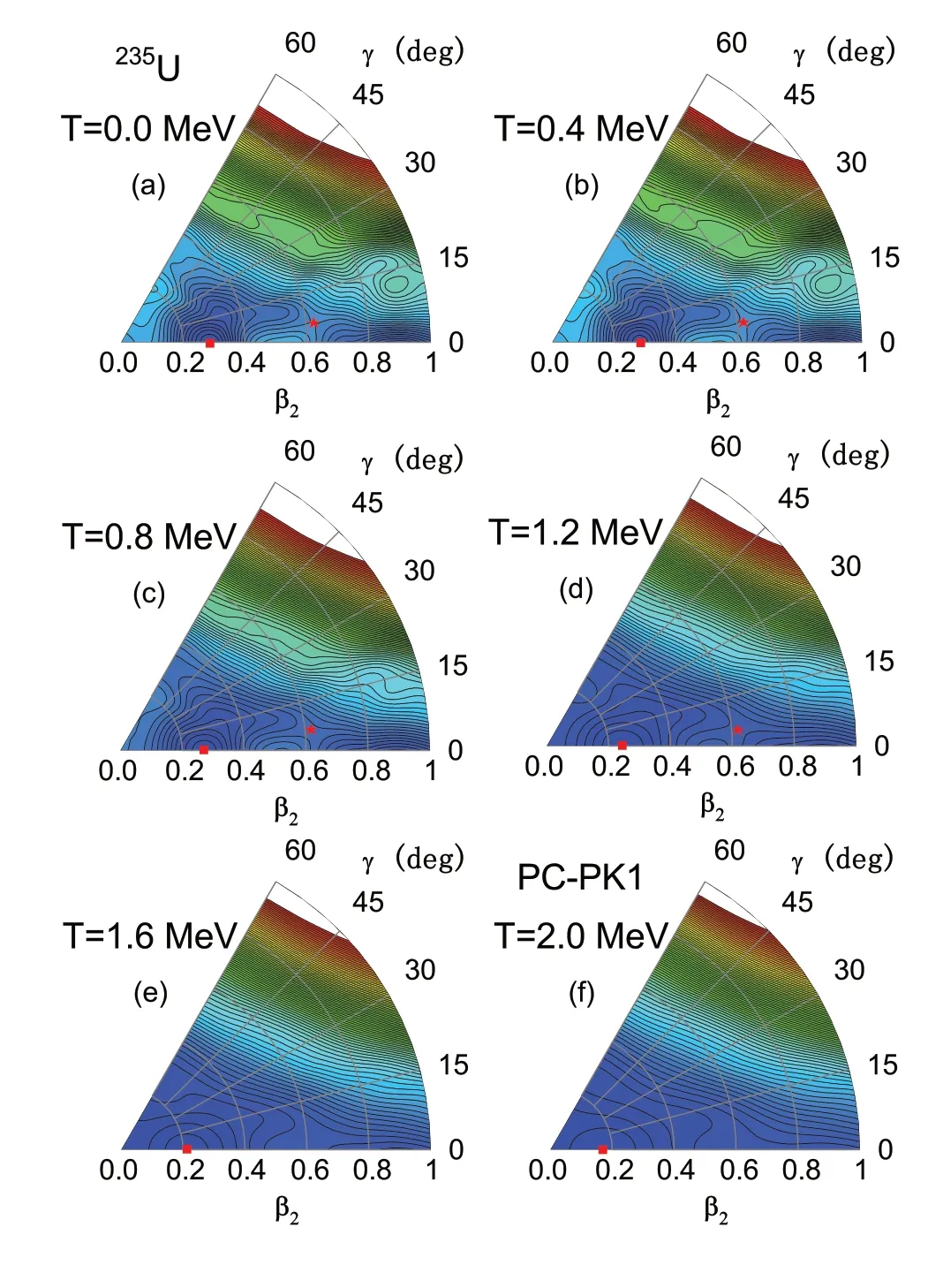
Fig.1 (Color online) Free energy surfaces in the ( β2,γ ) plane at temperatures of (a) 0, (b) 0.4, (c) 0.8, (d) 1.2, (e) 1.6, and (f) 2.0 MeV for 235 U obtained via finite-temperature CDFT calculations using the parameter set PC-PK1.The global minimum and saddle points are represented by squares and stars, respectively.The energy separation between contour lines is 0.5 MeV

In the nuclear reactions, the level density of the saddle point is critical.Figure 3 shows several properties of the saddle points with respect to the temperature for234-240U calculated with the parameter set PC-PK1, i.e., the excitation energiesEi, the entropyS, the specific heatCv, the partial derivative of the entropy with respect to the temperature∂S∕∂T, the pairing energy gap Δ , and the intrinsic level densityρi.The temperature range ends at 1.4 MeV,which corresponds to the excitation energy of approximately 40 MeV.For higher temperatures up to 2 MeV, the trends do not change.In Fig.3e, pairing phase transitions occur at a temperature of approximately 0.6 MeV for all nuclei.WhenT≈0.4 MeV, more curve details aboutCvand∂S∕∂Tin Fig.3c, d can be observed.ForCv, the curve reaches a local maximum and then decreases slightly, and the segmentsT ＜0.4 MeV andT ＞0.6 MeV are essentially two straight lines.Because the specific heat is the partial derivative of the excitation energy with respect to the temperature, it supports the fact that the excitation energy curves in Fig.3a are actually two connecting quadratic parabolas.This is consistent with the fact that in the Fermi-gas model, the intrinsic excitation energy increases quadratically with respect to the temperatureEi∝T2with slope changes around the pairing phase transition.For∂S∕∂T, it reaches 60 MeV-1, decreases to 40 MeV-1,and then remains constant forT ＞0.6 MeV.Because of the direct relationship between∂S∕∂Tand entropyS, the entropy should be quadratic forT ＜0.4 MeV and linear forT ＞0.6 MeV.This confirms the classic relationS∝Tbut only for high temperatures.The logarithmic intrinsic level densityρiin Fig.3f has analogous temperature dependence to the entropySin Fig.3b, representing ln(ρi)∝Sin Eq.(3).

Fig.3 (Color online) Excitation energy Ei (a), entropy S (b), specific heat Cv (c), ∂S∕∂T (d), pairing energy gap Δ (e), and intrinsic level density ρi (f) with respect to the temperature for saddle points of 234-240 U.The results were obtained via finite-temperature triaxial CDFT calculations with the parameter set PC-PK1

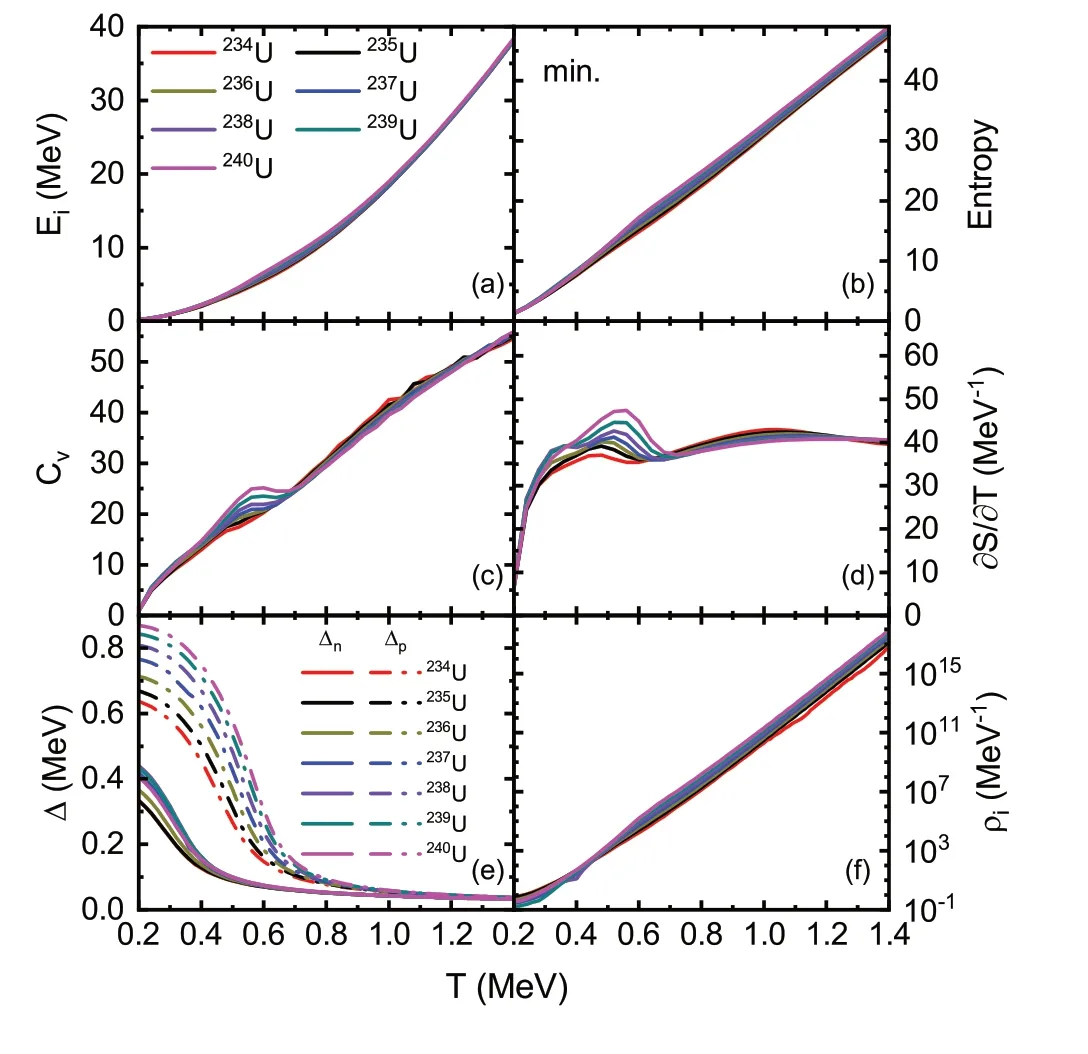
Fig.4 (Color online) Same as Fig.3, but for the global minimum

For comparison, the corresponding properties of the global minimum of234-240U are shown in Fig.4.In Fig.4e,the pairing phase transition occurs atTc= 0.6-0.7 MeV,while the proton gap is larger than the corresponding neutron gap at low temperatures.For the specific heatCvin Fig.4c, the slopes before and after the phase transition are close, rendering the excitation energy curve in Fig.4a a smooth parabola.At high temperatures, the partial derivative∂S∕∂Tin Fig.4d has nearly the same constant as that in Fig.3d.Because the intrinsic level density increases exponentially with respect to the entropy, this indicates that both the entropySin Figs.3b and 4b and the logarithmic intrinsic level density in Figs.3f and 4f have the same trends at a high excitation energy.

In addition, the result for the parameter set DD-LZ1 is obtained.The specific heatCvvaries more gently near the pairing phase transition, while other properties are roughly the same as those for PC-PK1.

In the second step, the collective level densities of odd-Anuclei are calculated via the CQC model, while those of even-even nuclei are obtained via the 5DCH model.The collective Hamiltonian of the odd-Anuclei is obtained by coupling the core parts of the two adjacent even-even nuclei and one particle or hole in the spherical case.The two free parameters of the model, i.e., the Fermi surfaceλand coupling strengthχ, are adjusted according to the experimental values of the low excitation spectrum.Details can be found in Ref.[69].The CQC parameters for the odd-A235-239U nuclei corresponding to two density functional parameter sets PC-PK1 and DD-LZ1 are presented in Table 1.

Take235U as an example.Its low excitation spectra obtained using PC-PK1 and DD-LZ1 together with the experimental data from the NNDC [73] are shown in Fig.5.The coupling strength and Fermi surface are finely tuned to reflect the collective enhancement induced by negative parity according to the corresponding experimental data of the low excitation spectrum.The calculated levels exhibit good qualitative agreement with the experimental results.

In the final step, when performing the convolution using the Eq.(1) to obtain the total level density, it is found that the total level densityρtotdepends on the number of collective levels considered.This implies that a specific collective truncation parameter should be introduced and adjusted manually.To alleviate this problem, inspired by Ref.[36, 74], a factor exp(-Ec∕T) is inserted into Eq.(1),and the total level density is rewritten as

Table 1 CQC parameters for 235,237,239 U based on triaxial CDFT calculations with the parameter sets PC-PK1 and DD-LZ1; the units of λ and χ are MeV and MeV/b,respectively

Fig.5 (Color online) Calculated low-energy positive-parity (a) and negative-parity (b) bands, of 235 U based on triaxial CDFT calculations with the parameter sets PC-PK1 (red) and DD-LZ1 (blue)together with the available experimental data (black) [73]

This factor simulates the coupling between the collective levels and intrinsic levels: higher collective levels correspond to a weaker contribution to the convolution; thus, a fixed truncation parameter is not needed.According to the highest excitation energy considered, tests reveal that an angular momentum up to 18ℏwith the first 20 collective levels for each angular momentum is sufficient.

Fig.6 (Color online) Total level densities (solid) and intrinsic level density (dash-dotted) at the global minima ( a-g ) and saddle points( a′-g′ ) of the 234-240 U with respect to the excitation energy E*.The pink and blue lines correspond to calculations with the parameter sets PC-PK1 and DD-LZ1, respectively.The experimental data (black squares) from Ref.[75] and calculations from Refs.[20, 22] are compared

In Fig.6, the total level density and the intrinsic level density at the global minima and saddle points are compared with available experimental data below 5 MeV [75], available calculations in the TALYS-1.95 package [1] directory density/ground/hilaire or density/fission/hilaire/Max1 and directory density/ground/goriely or density/fission/goriely/inner, or the Reference Input Parameter Library (RIPL) [20,22].Clearly, the intrinsic level densities deviate from the experimental data, indicating the necessity of collective degrees of freedom.For excitation energies up to 10 MeV,the total level density calculated via the two parameter sets PC-PK1 and DD-LZ1 agrees well with the two sets of theoretical calculations performed by S.Goriely and S.Hilaire in TALYS.However, for energies above 10 MeV, the total level density obtained via the relativistic density functional agrees well with Hilaire’s calculation, whereas Goriely’s calculation exhibits a sharp increase.The ratio of the total level density to Hilaire’s calculation resultρtot∕ρHilaireis well within an order of magnitude.

Furthermore, we compare the total level densities at the saddle pointsρsdand those at the global minimaρminand plot their ratio in Fig.7.For low excitation energies up to 5 MeV,the majority ofρsdvalues are smaller thanρmin, which may be related to pairing association [76].The pronounced peaks at 0-5 MeV for237-239U are actually caused by a small drop in the intrinsic level density at the global minimum (Fig.6).For intermediate energies in the range of 5 MeV＜E*＜30 MeV,ρsdincreases more quickly thanρmin.In particular, for235U, this ratio increases linearly with respect to the excitation energy.When the atomic number increases from234U to240U, the curve of this ratio tends to shift downward.

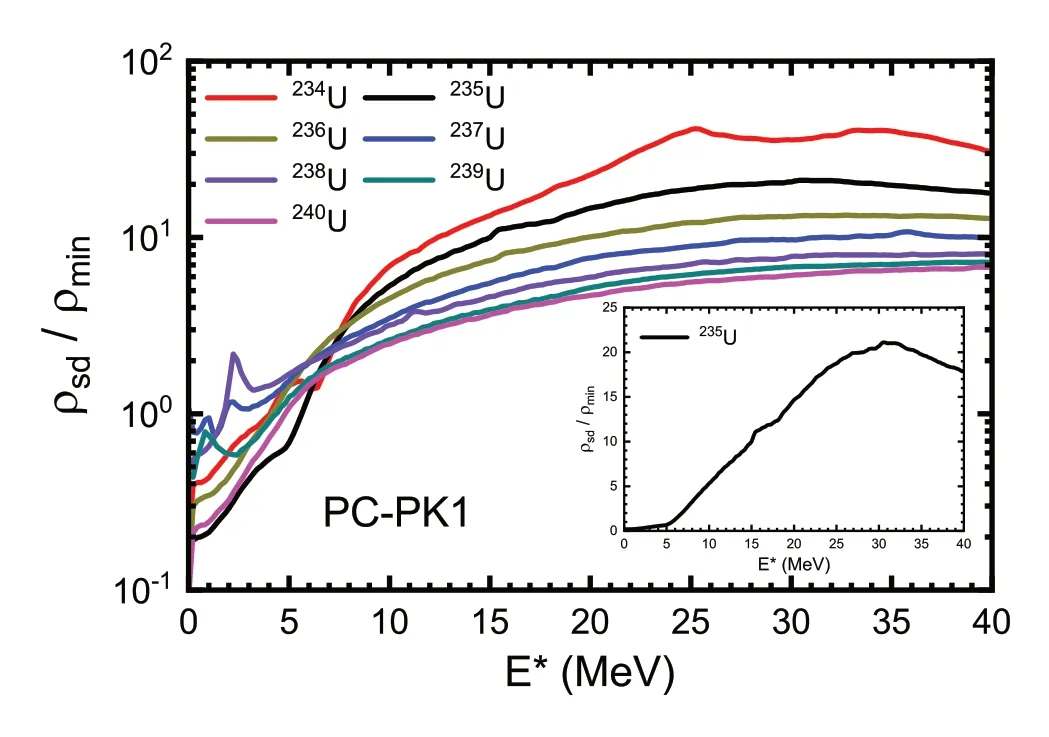
Fig.7 (Color online) Ratio of the total level density at the saddle point to that at the global minima ρsd∕ρmin in the logarithmic scale with respect to the excitation energy for 234-240 U based on triaxial CDFT calculations with the parameter set PC-PK1.The embedded subfigure is for 235 U in the linear scale

Fig.8 (Color online) Collective enhancement factor Kcoll with respect to the excitation energy for global minima of 234-240 U based on triaxial CDFT calculations with the parameter sets PC-PK1 and DD-LZ1

Finally, it is convenient to study the ratio of the total level density to the intrinsic level densityKcoll(E*)=ρtot(E*)∕ρi(E*) [30] as a collective enhancement factor and attribute it to the inclusion effect of collective levels.Figure 8 shows this collective enhancement factorKcollwith respect to the excitation energyE*for234-240U.Clearly,the curves can be divided into two groups: one group consists of low-lying concentrated curves for even-even nuclei234-240U, and the other group consists of scattered curves for three odd-Anuclei235-239U.This implies different collective spectrum patterns for even-even nuclei and odd-Anuclei.For even-odd nuclei, the factorKcollobtained via the parameter set DD-LZ1 exceeds that for PC-PK1.The magnitude ofKcollis similar to that of the nuclei94,96,98Mo,106,108Pd,and106,112Cd discussed in Fig.5a of Ref.[30] at the low excitation energy.The collective enhancement factor shown in this figure undoubtedly indicates the fact that the collective levels of odd-Anuclei are lower and denser than those of even-even nuclei.For level densities at saddle points,this factorKcollis almost indistinguishable from those of the global minimum.

4 Summary

Author ContributionsAll authors contributed to the study conception and design.Material preparation, data collection, and analysis were performed by Wei Zhang, Wei Gao, Gui-Tao Zhang, and Zhi-Yuan Li.The first draft of the manuscript was written by Wei Zhang and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Data availabilityThe data that support the findings of this study are openly available in Science Data Bank at https:// www.doi.org/ 10.57760/ scien cedb.j00186.00076 and https:// cstr.cn/ 31253.11.scien cedb.j00186.00076.

Declarations

Conflict of interestThe authors declare that they have no conflict of interest.