Constraining nuclear symmetry energy with the charge radii of mirror-pair nuclei

Rong An · Shuai Sun · Li-Gang Cao,2 · Feng-Shou Zhang,2,4

Abstract The nuclear charge radius plays a vital role in determining the equation of state of isospin asymmetric nuclear matter.Based on the correlation between the differences in charge radii of mirror-partner nuclei and the slope parameter (L) of symmetry energy at the nuclear saturation density, an analysis of the calibrated slope parameter L was performed in finite nuclei.In this study, relativistic and nonrelativistic energy density functionals were employed to constrain the nuclear symmetry energy through the available databases of the mirror-pair nuclei 36Ca-36 S, 38Ca-38Ar, and 54Ni-54Fe.The deduced nuclear symmetry energy was located in the range 29.89-31.85 MeV, and L of the symmetry energy essentially covered the range 22.50-51.55 MeV at the saturation density.Moreover, the extracted Ls at the sensitivity density ρs =0.10 fm-3 was located in the interval range 30.52-39.76 MeV.

Keywords Symmetry energy · Charge radii · Mirror nuclei

1 Introduction

Precise knowledge of nuclear symmetry energy (NSE),which is characterized as a component of the equation of state (EoS) of isospin asymmetric nuclear matter, can provide access to various physical phenomena relevant to a broad range of density profiles and energy scales [1, 2].NSE plays an important role in understanding the nuclear structure.Moreover, the behavior of NSE may affect the properties of neutron stars [3-5] and help to comprehend the supernova explosion mechanism and stellar nucleosynthesis in astrophysical studies [6].

The density dependence of NSE, that is,Es(ρ) , can be expanded around the saturation densityρ0( ≃0.16 fm-3) as follows:

whereLandKsymare the slope and curvature of the symmetry energy at the nuclear saturation densityρ0, respectively.The symmetry energy is believed to be associated with the isovector-sensitive indicators in the EoS of isospin asymmetric systems.Unfortunately, a direct connection between the experimental observables and the EoS is not possible.Consequently, the microscopic implications of NSE can be extracted indirectly from the ground and the collective excited state properties of atomic nuclei, reaction observables, and detected dense astrophysical events [7, 8].

Thus far, enormous efforts have been undertaken to determine the EoS over the spread of density profiles and energy scales [9].The neutron skin thickness (NST) of a heavy nucleus provides an available constraint on the EoS of neutron-rich matter aroundρ0[10-17].In the laboratory,the radius of208Pb has been detected by measuring parityviolating asymmetry in polarized elastic electron scattering experiments, for example, sequentially in the PREX-II [18].The accuracy of NST has been further updated from the latest performance, namelyR208skin=0.283±0.071 fm.The behavior ofEs(ρ) is mostly governed by the slope of the symmetry energy,L.The correlation betweenR208skinand the slope parameterLleads to a value ofL=106± 37 MeV [19].In addition, NSE can also be investigated using the isotope binding energy difference [20, 21] and double-magic nuclei[22, 23].

Significant progress has been made in evaluating NSE from the collective excited state properties of finite nuclei,such as isobaric analog states [24], pygmy dipole resonance(PDR) [25], electric dipole polarizability [26], giant dipole resonance (GDR) [27], isovector giant quadrupole resonance (IVGQR) [28], and charge-exchange giant resonance[29-32].The results forLextracted from PDR in68Ni and132Sn were constrained to be in the intervals 50.3-89.4 MeV and 29.0-82.0 MeV [25], respectively.The deduced slope parameter from the weighted average can cover the rangeL=64.8±15.7 MeV.As suggested in Ref.[28], the slope parameter of the symmetry energy can be reduced to 37±18 MeV by exploiting IVGQR energies.

Moreover, NSE offers a key requirement for our understanding of nuclear reactions under isospin diffusions and isotopic distributions [33-35].Heavy-ion collisions (HICs)provide a sensitive probe to link the nuclear EoS, which depends on isovector potentials.In transport models, NSE is derived by simulating isospin-sensitive observables [36-40].Hence, many simulation codes are desirable to determine the NSE [41-46].More details about the transport simulations can be found in a recent study [47].Meanwhile,new observations of compact stellar objects have provided plentiful data that help discern the EoS across saturation densities [48, 49].The range ofLcan be deduced from the observation of dense object events, such as the production of gravitational waves from the neutron star merger GW170817[50], resulting inL=11-65 MeV.

The density dependence of symmetry energy is fairly uncertain, except for the bulk properties at the saturation densityρ0.This challenges us in reducing the intrinsic uncertainties of the model from multiple aspects of the isovector components.As demonstrated in Refs.[51, 52],the difference in the root-mean-square (rms) charge radii of mirror-pair nuclei ( ΔRch) obtained using Skyrme functionals provides an alternative opportunity for calibrating the density dependence of NSE.

A related linear correlation between ΔRchand the slope parameterLhas been established.In Ref.[53], the differences in the charge radii of the mirror-partner nuclei36Ca-36S and38Ca-38Ar were investigated with varied values ofL.It is evident that the slope parameter lies in the rangeL=5-70 MeV.The latest precise determination evaluated the correlation between the difference in charge radii of the mirror-partner nuclei54Ni-54Fe and the slope parameter,which implied a range ofL=21-88 MeV [54].The rms charge radii of the nuclei54Ni and54Fe were obtained using Skyrme energy density functionals (EDFs) and covariant density functional theories (CDFTs), respectively.

As demonstrated above, ΔRchof mirror-pair nuclei can be employed to extract information aboutL.The latest results of the charge radii of54Ni can facilitate efficient exploration of the nuclear EoS.The experimental data forRchand ΔRchof the corresponding mirror partners are listed in Table 1[53-55].The NSE characterized as an isovector indicator in effective interactions should be systematically evaluated based on the latest experiments.To further obtain a comprehensive conclusion about the correlations betweenLand ΔRch, ΔRchfor the pairs of mass numbersA=36 , 38, and 54 can be calculated using nonrelativistic and relativistic(covariant) EDFs.Although the correlations between the incompressibility coefficients and isovector parameters are generally weaker than the correlations between the slope parameterLand symmetry energy [56], the uncertainty suffered from nuclear incompressibility is inevitable in the evaluated process.Therefore, the values of incompressibility coefficients characterized as isoscalar parameters are almost identical for the two types of EDFs.

The remainder of this paper is organized as follows: in Sect.2, we briefly report the theoretical models.In Sect.3,we present the results and discussion.Finally, a summary and an outlook are provided in Sect.4.

Table 1 Rch and ΔRch database for the A=36 , 38, and 54 mirror-pair nuclei.The parentheses beside the values of charge radii and the difference in charge radii are systematic uncertainties [53-55]

2 Theoretical framework

In this study, we adopted two types of widely used nuclear density functionals to extract information about the nuclear matter EoS, namely the sophisticated Skyrme and covariant EDFs.Both have achieved great success in describing the bulk properties of finite nuclei, such as binding energies and charge radii.For a detailed introduction to nonrelativistic and relativistic EDFs, refer to Refs.[57-59].In this paper, we briefly introduce the two nuclear density functionals.The effective interaction in sophisticated Skyrme-type EDFs, which is expressed as an effective zero-range force between nucleons with density-dependence and momentumdependence terms, is as follows: [60, 61]

where r=r1-r2and R=(r1+r2)∕2 are related to the positions of two nucleons, P=(∇1-∇2)∕2i is the relative momentum operator and P′is its complex conjugate acting on the left,σ=→σ1+→σ2, and Pσ=(1+→σ1+→σ2)∕2 is the spin exchange operator.The quantitiesα,ti, andxi(i=0-3)represent the parameters of the Skyrme forces.

For covariant EDFs, the interacting Lagrangian density has the following form: [62, 63]

Here, Ωμν=∂μων-∂νωμ,→Rμν=∂μ →ρν-∂ν →ρμ-gρ(→ρμ×→ρν),Fμν=∂μAν-∂νAμ, andM,mσ,mω, andmρare the nucleon,σ , ω , and ρ meson masses, respectively.The quantitiesgσ,gω,gρ,g2,g3,c3, ande2∕4π=1∕137 are the coupling constants for the σ , ω , ρ mesons, and photons.The parameter set Λvrepresents the coupling strength between theωandρmesons.Solving the Skyrme HF and Dirac equations on a spherical basis, one can obtain the eigenenergies and wave functions of the constituent nucleons, from which the bulk properties of the ground states can be obtained using this standard procedure [57-63].

In our applications, two families of parameter sets were adopted: the asy family for Skyrme EDFs [64] and the IUFSU family for covariant EDFs [65].All of these effective forces were calibrated by fitting the parameters to specific observables of finite nuclei, such as binding energies and charge radii, and the isovector part of the EoS was generated in such a way that the symmetry energy remained at a fixed value ( ≈ 26 MeV) around a sensitivity baryon density ofρs≈0.10 fm-3; thus, the interactions were characterized by different values of the symmetry energy at saturation density.This procedure ensures that the quality of the fit cannot be contaminated and that all isoscalar observables remain unchanged, for example, the incompressibility coefficient almost equals 230 MeV.In Fig.1, the density dependence behaviors of the symmetry energies are plotted using the relativistic and Skyrme EDFs.With increasing symmetry energy at the saturation densityρ0≃0.16 fm-3,the slope became larger for these two families of parameter sets.For the symmetry energy around the sensitivity densityρs=0.10 fm-3, these values were almost unchanged.Further details can be found in Refs.[65, 66].It is worth mentioning that both the symmetry energies and slope parameters can cover a wide range.To reduce the intrinsic uncertainties of the models, such parameterization sets should be expected to provide stringent constraints on observables that are highly sensitive to the density dependence of the symmetry energy.The corresponding values of the bulk properties of the nuclear matter are shown explicitly in Table 2.

Fig.1 (Color online) Symmetry energies characterized by relativistic EDFS (a) and Skyrme EDFs (b) plotted as a function of density

Table 2 Models used for the calculation of Rch.The corresponding bulk properties of nuclear matter used in this study, such as symmetry energy Es (MeV), the slope parameter L (MeV), and the incompressibility K∞ (MeV) at saturation density, are given

3 Results and discussion

The results for ΔRchare plotted as functions ofLin Fig.2.The nonrelativistic Skyrme approach and RMF theory were used to assess the correlation between ΔRchandL, which are shown by the open circles and crosses in Fig.2, respectively.The horizontal light blue bands indicate the uncertainties of ΔRch, which correspond to 0.146-0.154 fm (36 Ca-36S), 0.060-0.066 fm (38Ca-38Ar), and 0.045-0.053 fm(54Ni-54Fe).The linear fits in the correction for ΔRchare indicated by the dashed lines.

The results obtained using the Skyrme and covariant EDFs revealed an approximate linear correlation between ΔRchandL.Constraints onLwere deduced by comparing the theoretical predictions with the experimental results in Fig.2.Note that the results forA=54 provided the slope of symmetry energyLrelevant to the range 17.99-62.43 MeV,whereas those forA=38 andA=36 were in the intervals 6.83-52.49 and 22.50-51.55 MeV, respectively.We can see that these values essentially cover the theoretical uncertainties in Refs.[53, 54].

The NST of48Ca is regarded as a feasible isovector indicator to constrain the EoS of nuclear matter.The high-resolutionE1 polarizability experiment performed at RCNP suggests that the NST of48Ca is located in the interval 0.14 ～0.20 fm [67].Meanwhile, the CREX collaboration has reported a new value through parity-violating electron scattering measurements, namely 0.071 ～0.171 fm [68].The NST of48Ca allows a direct comparison to microscopic calculations using various slope parameters,L.In Refs.[69, 70], the linear correlation analysis of ΔRchof mirror-partner nuclei and the corresponding NST has been clearly illustrated.Therefore, it is essential to evaluate the correlations between ΔRchof mirror-pair nuclei and the NST of48Ca.

Fig.2 (Color online) ΔRch of the mirror-partner nuclei 36Ca-36 S (a),38Ca-38 Ar (b), and 54Ni-54 Fe (c) as a function of the slope parameter L at the saturation density ρ0.The experimental result is shown as a horizontal light blue band.The crosses are results of relativistic EDFs, and the open circles are for the Skyrme EDF calculations.The dashed lines indicate theoretical linear fits

The correlations between ΔRchof theA=36 , 38, and 54 mirror-partner nuclei and the NST of48Ca ( ΔRnp) are also shown in Fig.3.The calculated ΔRchsubstantially covered the current uncertainties of ΔRnp(48Ca) for both types of EDFs.For theA=54 mirror-pair nuclei, the Skyrme model gave a comparable correlation with respect to the RMF model.A high linear correlation between ΔRchofA=54 and ΔRnpof48Ca was found.These correlations were also obtained using nonrelativistic and relativistic EDFs for theA=36 and 38 mirror partners, as shown in Figs.3 a and b.This means that information on symmetry energy can be extracted from the differences in the charge radii of mirror-pair nuclei.

Fig.3 (Color online) “Data-to-data" relation between ΔRch of the A=36 , 38, and 54 mirror-partner nuclei and the neutron skin thickness ΔRnp of 48Ca.The labels and color coding are the same as those used in Fig.2

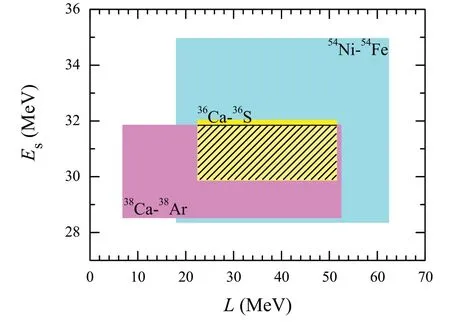
Fig.4 (Color online) Symmetry energy Es and the slope of symmetry energy L are limited by ΔRch of the A=36 (yellow plane), 38 (light purple panel), and 54 (light blue plane) mirror-partner nuclei.The shadowed plane represents the result of the theoretical prediction in this study

To obtain further constraints on the EoS of asymmetric nuclear matter, the relationship between the symmetry energy at saturation density and ΔRchof mirror-pair nuclei can also be evaluated as well as the relationship betweenLand ΔRch.Therefore, the “Data-to-data" relationships between the symmetry energies and the slope parameters are shown in Fig.4 via various colored planes for theA=36 (Ca-S), 38 (Ca-Ar), and 54 (Ni-Fe) mirrorpartner nuclei.The shadowed plane represents the result of the theoretical prediction.From this figure, it is noticeable that the deduced symmetry energy was located in the intervalEs=29.89-31.85 MeV, and the slope of the symmetry energy covered the rangeL=22.50-51.55 MeV.It should be mentioned that the present value provides a tighter constraint onLthan those in Refs.[53, 54].Although the mirror-partner nuclei for the massesA=36 , 38, and 54 were simultaneously considered in our evaluated procedure, the effects of deformation and model uncertainties were not incorporated in our calculations as in Refs.[53,54].In forthcoming investigations, we will carefully study the effect of deformation on the charge radius of finite nuclei and estimate the model uncertainties using a comprehensive set of modern density functionals, which may change the present results.

To facilitate the quantitative comparison of the extracted results with the theoretical calculations, various available estimates of the slope parameterLof the symmetry energy are shown in Fig.5.It is evident that our present result has a remarkable overlap with the results obtained by various methods or observables.Our calculations predominantly covered the result forLextracted from PDR in132Sn (L=29.0-82.0 MeV) but deviated from that of68Ni(L=50.3-89.4 MeV) [25].Figure 5 shows the weighted average value in the interval of 64.8±15.7 MeV.In addition, the electric dipole polarizability of a heavy nucleus is highly sensitive to both the magnitude and slope parameter of symmetry energy, providing a value ofL=47.3±7.8 MeV [26].By exploiting this correlation together with the experimental values of the isoscalar and isovector giant quadrupole resonance (GQR) energies, the slope parameter of the symmetry energy was estimated asL=37± 18 MeV[28].Both theoretical results essentially covered the current uncertainty in this study.

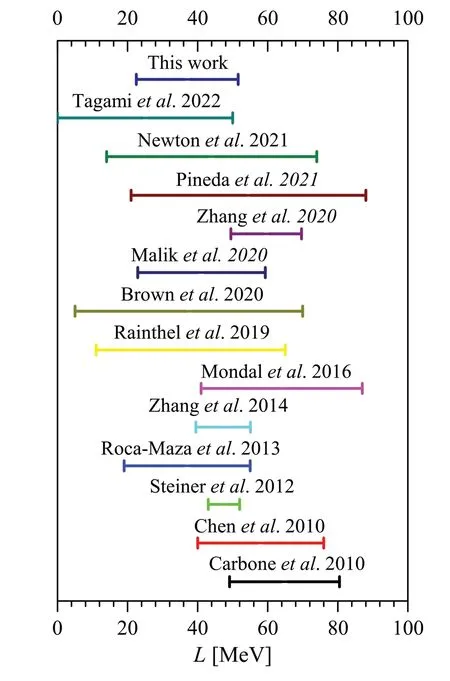
Fig.5 (Color online) Comparison between the values of L extracted in this study and those from existing literature.We partly compare the values extracted from various models: Carbone et al.[25], Chen et al.[71], Steiner et al.[75], Roca-Maza et al.[28], Zhang et al [26],Mondal et al.[13], Raithel et al.[50], Brown et al.[53], Malik et al.[76], Zhang et al.[74], Pineda et al.[54], Newton et al.[80], and Tagami, et al.[72]

The NST Δrnpin heavy nuclei provides an alternative terrestrial probe to place restrictions on the nuclear EoS.In Ref.[71], an accuracy value ofL=58±18 MeV was deduced by analyzing the neutron skin data on Sn isotopes and the observables originating from HICs.Our calibrated results covered the uncertainty of this value.The latest NST of48Ca detected by the CREX group yielded the slope parameterL=0 ～50 MeV [72], which is in accordance with this study (L=22.50-51.55 MeV).Significantly, the NST of208Pb detected by the PREX-II group yielded a larger value ofL=76 ～165 MeV.Reed et al.[19] reported a comparable interval of the slope parameterL=106±37 MeV.These values partially cover the interval range ofL=54 ～97 MeV induced by HICs [73].However, the evaluated range in this literature has no overlap with the slope parameterLobtained by PREX-II.

In Ref.[74], more information, such as heavy-ion collision data, the neutron skin of208Pb, tidal deformability,and the maximum mass of neutron dense objects, was used to calibrate the values of symmetry energy.This led to a symmetry energy slope ofL=59.57±10.06 MeV, and the quantitative uncertainty was further reduced with respect to Ref.[71].Moreover, the slope parameterLcan be constrained by various observed astrophysical messages,except in terrestrial nuclear experiments.The currently available neutron star mass and radius measurements provide an important constraint on the EoS of neutron matter through quantum Monte Carlo simulations, in which the slope parameterLis located in the range 43-52 MeV [75].The correlation of the tidal deformability of a neutron star withLwas studied using the skΛ267 model, which gave the rangeL=41.1±18.2 MeV [76].Moreover, the rangeL=11-65 MeV was extracted from the observation of a gravitational-wave event of the neutron star merger GW170817 [50].Our calibrated range (L=22.50-51.55 MeV) overlaps significantly with these deduced values.

Recently, emerging Bayesian frameworks have been developed widely to study the bulk properties of finite nuclei, for example, predictions in the nuclear charge radii[77, 78] and nuclear EoSs [79].The existing database of neutron skin and the bulk properties of nuclear matter are characterized by prior input quantities, which leads to credible values ofandL=37+9-8MeV[80], respectively.All the evaluated values are consistent with the range ofLobtained in this study.

As mentioned in Refs.[81, 82], the density dependence of the symmetry energy at the subsaturation density is associated with nuclear mass differences and multifragmentation production.Thus, it is also interesting to give the constraint of the slope parameterLsat the sensitivity densityρs=0.10 fm-3probed by the differences in the charge radii of mirror-partner nuclei ( ΔRch).In Fig.6,ΔRchof the mirror-partner nuclei36Ca-36S (a),38Ca-38Ar(b), and54Ni-54Fe (c) as a function of the slope parameterLsat the sensitivity densityρs=0.10 fm-3are plotted.The highly linear correlations between ΔRchandLsare also presented.The extracted interval range of the slope parameterLsat the sensitivity densityρs=0.10 fm-3was approximately 30.52-39.76 MeV.This restricted value is relatively narrow compared to the interval range at the saturation densityρ0≃0.16 fm-3.

Fig.6 (Color online) Same as Fig.2, but for the slope parameter Ls at the sensitivity density ρs =0.10 fm-3

4 Summary and outlook

Microscopic methods based on families of nonrelativistic and relativistic EDFs were employed to characterize a systematic variation of the isoscalar and isovector properties of corresponding nuclear matter EoSs.Our systematic analysis of the extraction of the slope parameterLfrom the differences in mirror-partner nuclei charge radii provided a new result.The slope parameterLcovered the interval range 22.50-51.55 MeV at the saturation density.Moreover, the slope parameterLsat the sensitivity densityρs=0.10 fm-3lay in the interval range 30.52-39.76 MeV.This led to us determining the density dependence of symmetry energy relatively accurately, which is a fundamental quantity for nuclear physics and for the implications in the study of neutron stars.

Linear fits were performed between the differences in the charge radii of mirror-partner nuclei and the slope parameterL.As suggested in Refs.[83-87], precise descriptions of the nuclear charge radii are influenced by various mechanisms.Meanwhile, the precise measurement of the charge density distributions usually affects the NST of finite nuclei on a quantitative level.In Ref.[88], it is demonstrated that the differences in the charge radii of mirror-pair nuclei are systematically influenced by the pairing correlations.For weakly bound nuclei, configuration mixing should be discreetly considered when tackling pairing correlations [89].Hence, this study should be further reviewed.

Author ContributionsAll authors contributed to the study conception and design.Material preparation, data collection, and analysis were performed by Rong An, Shuai Sun, Li-Gang Cao, and Feng-Shou Zhang.The first draft of the manuscript was written by Rong An and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Declarations

Conflict of interestFeng-Shou Zhang is an editorial board member for Nuclear Science and Techniques and was not involved in the editorial review, or the decision to publish this article.All authors declare that there are no competing interests.