板式表面张力贮箱推进剂重定位过程数值仿真的网格收敛性分析
2023-09-18戴炜张钟元李光昱韩伟
戴炜,张钟元,李光昱,韩伟
1.南昌航空大学 飞行器工程学院,南昌 330063
2.军事科学院 国防科技创新研究院,北京 100071
1 引言
微重力环境下,气液高度混合,需要卫星贮箱内的推进剂管理装置对推进剂进行有效管理,实现气液分离,为推进系统提供不夹气的推进剂。板式表面张力贮箱以其质量轻、可靠性高的优点被广泛应用于多型号卫星[1-3]。在板式表面张力贮箱的设计过程中,需要对其性能进行验证。目前落塔试验有效时间短[4]、微重力飞机试验成本过高[4-6],都难以对板式表面张力贮箱性能进行大量、长周期的验证。随着计算流体力学(CFD)和计算机技术的迅猛发展,通过数值模拟技术对卫星贮箱性能进行仿真成为热点[7,8],极大提高了板式表面张力贮箱的设计和优化效率。
根据计算流体力学理论可知,在合理的参数设置下,数值仿真的误差随着网格数量的增加而逐渐减小直至收敛[9]。长期以来,工程人员常通过提高网格密度来提高仿真结果的精确度。然而,随着网格数量的增加,所消耗的计算成本以及计算时间也增加,因此需要对网格收敛性即网格无关性进行验证。在满足精度要求的情况下,较少地消耗计算资源。
针对网格收敛性验证问题,早在1994年,Roache[10-11]基于Richardson外推法,提出了网格收敛指数(Grid Convergence Index,GCI)用以评估网格模型。郑秋亚[12]等通过将网格逐步细分或粗化,采用GCI指数对网格无关性进行评估,选择一个理想的网格,做到既经济又能达到一定的精度要求。刘厚林[13]等通过对比得出GCI指数随着网格的加密会不同程度的减小,且由于网格越密离散结果越接近精确解。安恩科[14]等通过对比实验亦得出了同样的结论。Chung[15]等通过GCI指数分析液氢贮箱模型的收敛情况,获得了效率较高的仿真模型。以上研究均表明通过GCI指数能够较好地验证CFD数值仿真中网格的收敛性。目前部分仿真研究,对仿真模型并未进行网格收敛性分析,仿真效率较低。
本文以板式表面张力贮箱的应用为背景,首先建立了2.67L板式表面张力贮箱的几何模型,并对该模型离散化,生成了不同数量网格;然后对贮箱在50%、 60%填充率时的重定位过程进行了数值仿真。基于仿真结果,通过计算GCI指数,对不同网格数量的仿真模型进行网格无关性分析选出兼顾计算速度与精度的仿真模型;最后基于该模型计算不同方向扰动下贮箱质心的变化,以检验其抗外部扰动的能力。
2 板式表面张力贮箱仿真模型
2.1 物理模型
贮箱模型为球冠加圆柱段箱体(如图1所示),球面直径为120mm,圆柱段长度160mm,总高度为280mm,容积为2.67L。箱体内部安装有6片内导流板和6个外导流板,使得该贮箱具有较强的推进剂蓄留及导引能力[16]。内外导流板成30°夹角均匀分布在中央支撑柱周围。贮箱底部有24片叶片组成的蓄液器,用于卫星机动过程中蓄留推进剂,为推进系统提供推进剂。

图1 2.67L板式贮箱模型
仿真中贮箱内选择的工质为液态水,贮箱顶部留有气垫,选择工质为空气,其密度为1.225kg/m3,粘度为1.7894×10-5kg/m•s。液态水的相关参数如表1。
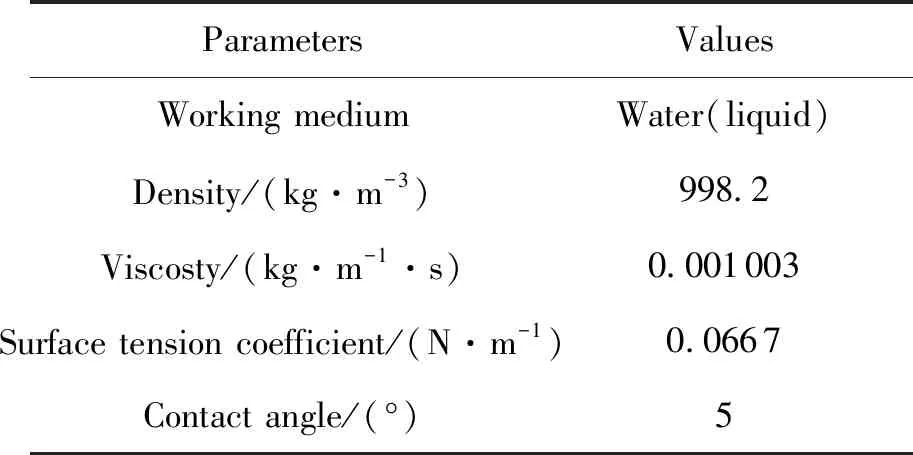
表1 工质的相关参数
2.2 网格划分
根据贮箱物理模型,建立仿真分析模型。采用非结构四面体网格划分方式(如图2所示)对贮箱内部流域进行离散化。

图2 2.67L板式贮箱网格模型
通过调整网格密度及边界层的数量(如图3所示),得到网格密度不同的四个模型。如表2所示
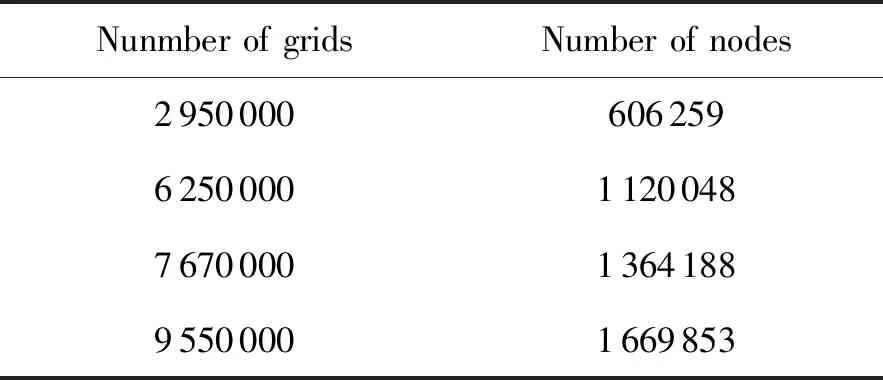
表2 4组网格的基本参数

图3 4种不同密度的模型在XY平面(z=0)的体网格截图
2.3 仿真参数设置
为模拟流体在贮箱内的流动情况,设置为非定常流动,不考虑重力的影响。各个壁面均定义为无滑移边界。选用VOF模型,设定初始状态下液体保持在贮箱底部,气体保持在贮箱顶部。将空气作为基本项,第二相为液相。湍流模型为Laminar模型。不考虑液体流动过程中的能量传递和热交换。
设置压力-速度耦合方程求解算法为PISO方式,梯度插值方案采用Green-Gause Cell Based法,压力插值算法选择Body Force Weighted,动量方程选用QUICK方法。
本文分别按照推进剂50%和60%的填充比,设定各相组分的初始条件,建立气液交界面并对其运动过程进行监测。监控并记录气液交界面最高点的位置,以推进剂爬升的最高点为仿真结果分析仿真模型的收敛情况。
3 网格收敛指数
假设数值仿真过程中存在仿真收敛解f与真实解f[exact]。则f可表示为:
f=f[exact]+g1h+g2h2+g3h3+…
式中:h为网格间距,gi为与步长无关的常数。令g1=0,得到:
令网格间距比r=h2/h1,hi为不同网格数模型对应的网格间距。又因在同一组对比网格中,模型未发生改变,模型总体积不变,故:
f[exact]≅f1+(f1-f2)/(r2-1)
式中:Ni为节点数;p为收敛率;ε为收敛误差;fi为不同网格模型得到的收敛解。
基于以上计算,Roache引入了一个安全系数Fs,通常Fs被设置为1.25~3之间[17]。定义网格收敛指数为:
GCI=Fs|E|
由于本次仿真网格数量采用非定常数量增加,则其收敛率p可由以下方程解出:

(1)
式中:ε12、ε23为选定考察项目的网格收敛误差;r为网格增长率,r的下标为3套不同的网格,编号分别为1、2、3;r12、r23为对应网格数量增长率。则网格收敛指数(GCI)定义为:
4 讨论与分析
4.1 仿真结果
不同于地面环境,卫星运行在微重力环境下,表面张力占主导地位。贮箱内的推进剂在表面张力的作用下,将沿导流板及贮箱壁面形成的内角流动。当贮箱推进剂达到最小势能状态时,气液交界面按一定的曲率半径附着在导流板板壁周围。此时贮箱内液体呈连续分布,气体被包裹在贮箱顶部。当贮箱受到扰动时,例如卫星调姿时,贮箱气液界面被破坏,当扰动停止时,推进剂在表面张力的作用下进行重定位,恢复到稳定的气液界面。为了保证卫星两次调姿时推进系统正常运行,需要获得贮箱推进剂在扰动停止后的重定位时间。
图4的数据来源于第二套模型(网格数为625万的模型),显示了贮箱60%填充率时重定位过程的仿真情况。图4(a)为仿真初始状态下气液交界面的形状,当重力消失,推进剂在表面张力的作用下沿罐壁和导流板爬升,气液交界面由平面逐渐收缩成弯液面。图4(d)为重定位完成时气液交界面的形状。

图4 60%填充率时液面爬升趋势图
4.2 不同网格数量结果
汇总4组不同网格的计算结果,绘制推进剂液面最高点的轨迹图。如图5所示,流动趋势保持一致,气液分界面的最高点相差较小。相较于网格数为295万的仿真模型,其余3组模型的重定位时间和液面高度曲线与文献[16]中的理论计算结果基本吻合且重定位时间相同,均为0.75s左右。为保证仿真过程中流场内的计算精度大致相同,要求网格的疏密程度相合理。对比图2网格剖面,网格数为295万的模型在贮箱边缘附近网格单元质量较差,且各导流板间的流域内网格疏密程度和排列方式均不相同。通过对数据后处理分析,该模型难以对接近壁面处推进剂的流动情况进行较高精度的仿真。
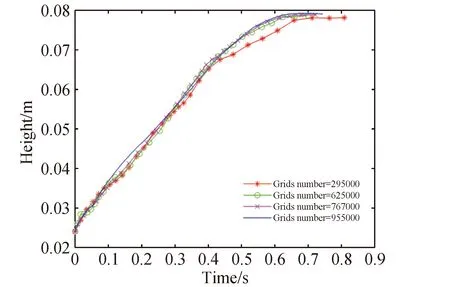
图5 60%填充率下4种网格模型液面爬升过程对比
通过观察图4中推进剂重定位过程中的气液交界面知,贮箱导流板具有良好的导流能力,且推进剂的最高点在内导流板的根部附近。为评估仿真模型对计算结果的影响,对仿真结果进行网格收敛性的分析。在评估过程中以气液分界面最高点的值作为对比量,为消除仿真计算过程中舍入误差的影响,每组工况均重复计算3次,分析数据并对差别过大数据予以剔除并求取计算平均值。汇总相关计算数据。如表3所示:

表3 不同填充率下仿真结果
其中L1为60%填充率液面最高点,L2为50%填充率液面最高点。
4.3 网格无关性对比分析
为检验贮箱重定位模型的网格收敛性,基于表3得到的仿真结果进行计算。由网格收敛指数定义知,收敛率p与网格模型有关。因为在建模时采用非结构化网格的网格划分方式,故网格间距的比值r为非定常量。因此在按式(1)计算收敛率p时,无法统一计算收敛率。所以将4组模型将数据按编号分为(1,2,3)、(2,3,4)、(1,2,4)和(1,3,4)共计4组对比组。Roache[16]指出,当对比组内存在3项数值时,此时安全系数Fs=1.25,带入公式(2)分别计算每组网格的网格收敛指数GCIfine和GCIcoarse。计算结果如表4所示。

表4 60%填充率GCI指数计算结果
通过对比四组对比组的数据,当加注量在60%时四组网格的网格收敛指数(GCI)均在1%以内,符合小于3%的要求[14]。且随着网格数量的增加,网格收敛指数呈下降的趋势,且网格收敛指数趋于0。
Ali等[18]在Roache的基础上,定义了收敛比R的概念:
若0
为验证上述结论,对50%填充率下,不同网格数量的仿真结果进行分析。如表5所示。在50%加注量时,网格数为295万的模型的计算结果相较剩余3组模型有较大偏差,使得其在网格收敛指数计算结果偏离正常值,甚至对比组(1,2,4)无正数解。且当充液量为50%时第1、3、4对比组的网格收敛比R>1,仅有第2对比组的网格收敛比在区间(0,1)内。符合收敛条件。综合以上计算,当充液量为50%时,仅有第二对比组的网格符合收敛条件。从而得到网格数量分别为625万、767万和955万的三组网格组成的网格组收敛。

表5 50%填充率GCI指数计算结果
通过比较4组不同数量网格的仿真模型,结果表明,网格数量分别为625万、767万和955万的仿真模型仿真收敛,能够满足目标精度。其中数量为625万时,不同工况的仿真结果已具有较高精度。经对比,网格数为625万、767万和955万的仿真模型计算耗时分别为8小时、10小时和13小时。综合考虑网格数为625万的模型计算时间较少,具有较高性价比。
4.4 贮箱受扰动情况下的重定位过程
卫星在轨运行时,根据其任务不同,需要进行在轨机动及轨道保持。为验证贮箱在轨运行时的抗扰动能力,针对卫星脉冲的典型工况[19,20],分别对贮箱50%填充率时受到周向和轴向扰动的质心晃动情况进行仿真分析。由于贮箱为轴对称结构,故仅模拟沿-X方向及-Z方向受到外部扰动的情况。设置扰动时长为1s,扰动大小为1.4×10-2m/s2。分析并记录扰动过程整体质心的变化,用以对比不同扰动对重定位过程的影响,以检验贮箱抗扰动的能力。
图6显示了贮箱质心坐标在不同扰动下的变化情况。当受到-X方向扰动时,X轴质心偏移量随时间逐渐加大,最大值为7×10-4m,此时Y轴质心偏移量经历小幅度波动后,逐渐恢复基本与无扰动时相一致。对比Z方向的质心坐标,无论是受到-X向还是-Z向扰动,其坐标曲线基本重合,最大偏移量仅为5×10-5m。如表6所示。由图可知,贮箱周向扰动对贮箱质心的影响较轴向扰动更大,但总体变化小于10-3m,因此单方向的扰动对其他方向的质心坐标影响亦十分有限。
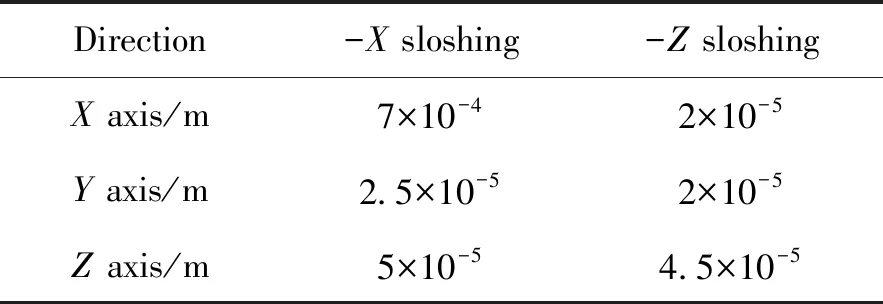
表6 各坐标轴重心最大偏移量
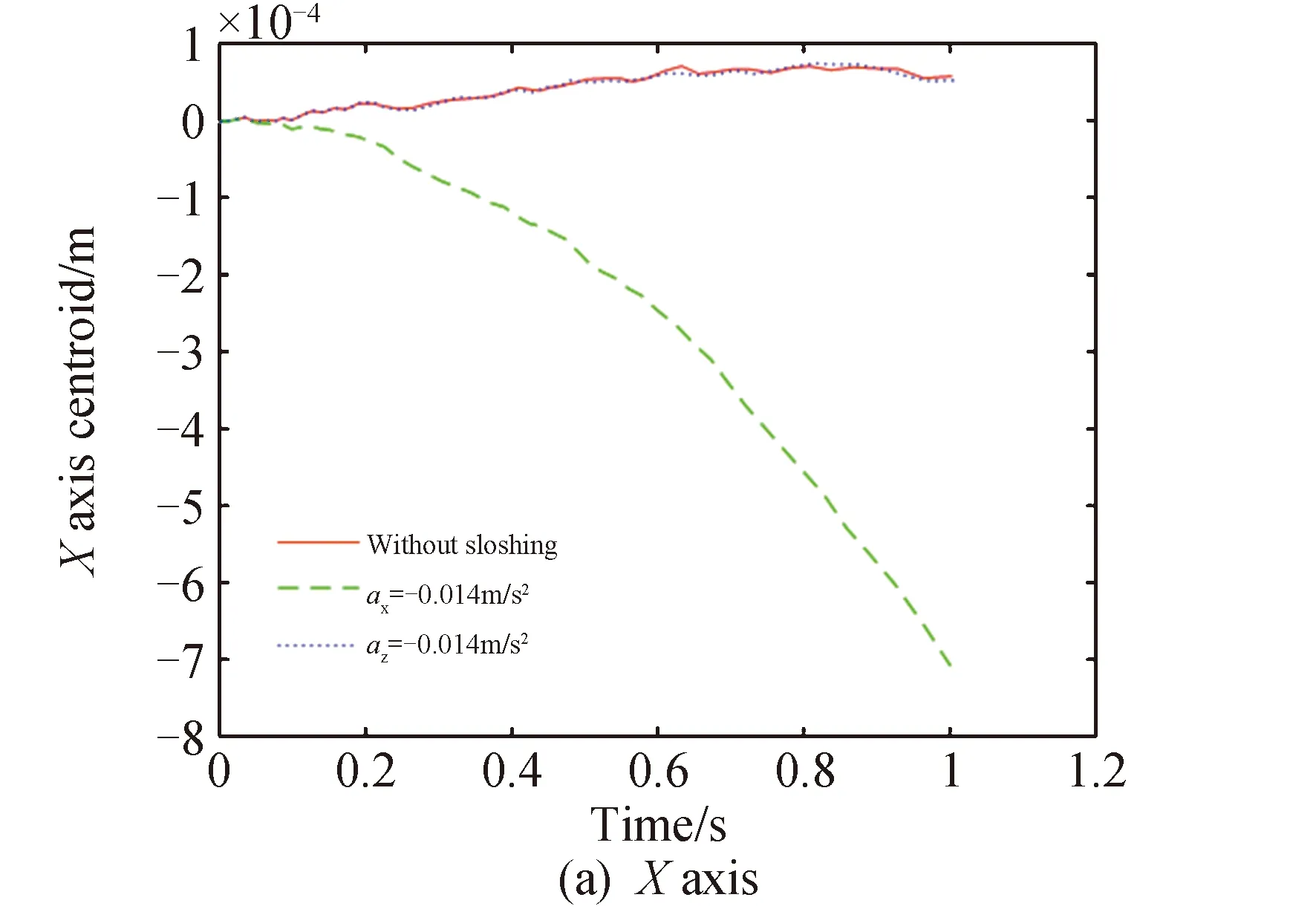
图6 质心坐标在不同扰动下的对比图
通过与无扰动时对比,在施加外部扰动下,质心各坐标轴的变化较小,小于10-3m。因而认为该贮箱有较好的抗扰动能力。该结果符合设计时同时采用内外导流板的初衷。
5 结论
论文以板式表面张力贮箱的典型工况仿真为背景,建立了2.67L板式表面张力贮箱的几何模型以及不同网格数量的仿真模型,通过计算不同贮箱模型在填充率为50%和60%时重定位仿真结果的GCI指数,进行网格收敛性分析。结果表明:在2.67L贮箱推进剂重定位仿真过程中,对于网格数为625万、767万和955万的仿真模型对比组,其数值模拟的误差逐渐收敛,数值模拟的计算值结果不会因网格数量不足而失真。综合考虑各方面的因素,选择网格数为625万的网格具有较高计算效率,用于板式贮箱后续工况的仿真计算。基于该仿真模型,分别对贮箱受到轴向、周向1.4×10-2m/s2加速度扰动以及不受扰动情况下的质心变化进行分析,质心变化小于1×10-3m,认为该贮箱具有较好的抗扰动能力。
通过监测外加扰动下贮箱质心的变化,得到在加速度为1.4×10-2m/s2的外加扰动下,贮箱内的液面管理装置能有效的抑制液面晃动。
