基于深度子领域自适应的直驱风机次/超同步振荡源定位

郝 琪，刘崇茹，王瑾媛，王鑫艳，苏晨博，郑 乐

（1.新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2.清华大学电机工程与应用电子技术系，北京市 100084）

0 引言

随着“双碳”政策的落实推进，以风能为代表的清洁可再生能源逐渐代替传统化石能源，在能源供给侧逐步占据主导位置。然而，新能源场站与电网的交互特性复杂多变，导致互联系统产生的振荡形态更加多样化，从而诱发频段愈发宽广的次/超同步振荡，严重威胁电力系统的安全稳定运行。例如，2015 年中国新疆哈密地区出现直驱风电场与弱交流系统交互作用产生持续的次/超同步振荡，造成多台机组相继脱网［1］。考虑到风电规模的日益增大，为了采取更为有效的次/超同步振荡抑制措施，亟须在众多风电机组中快速、准确地进行振荡源机组的识别与定位，这对避免振荡进一步扩散、保证系统的安全稳定运行具有重要意义。特别指出，本文实际系统次/超同步振荡源是指与系统发生交互，引发系统次/超同步振荡的风电机组。

目前，振荡源定位常用的方法有行波检测法、能量法、混合动态仿真法等。行波检测法将振荡的传播看作是行波在电网中的移动［2］，以振荡机电波峰值总是最早出现在振荡源处的理论为基础［3］，通过比较各测量点记录到行波波头最大值对应的时刻，进而来定位振荡源［4-5］。该方法响应速度非常快，但当振荡源距离电压测量单元较近时会失效。能量法通过构造能量函数，根据能量在系统中的传播路径即可判断出振荡源所在的位置，是一种基于机理分析的数值仿真方法，广泛应用于低频领域［6-9］。但由于次/超同步振荡频带较宽，诱发机理复杂，采用能量法分析含新能源电力系统次/超同步振荡问题的普适性还有待考证。另外，能量法的应用需基于一定的假设条件，在电力系统实际运行时，这些假设条件可能无法满足，这会导致定位的偏差较大［10］。混合动态仿真法基于系统仿真模型，仿真结果与实际测量数据之间差距较大的区域即为振荡源所在范围，通过多次迭代来获得精确振荡源位置［11-12］。该方法原理简单易懂，但需要大量的迭代时间。因此，通常只用于振荡的事后分析。

伴随电力系统结构的多元化和动态特性的强非线性化，从物理机理角度出发进行次/超同步振荡定位、识别的研究愈发困难。机器学习因其强大的处理非线性问题的能力被引入振荡源定位领域。文献［13］针对强迫振荡，考虑量测误差和系统变化的影响，提出了基于集成学习的振荡源定位方法。文献［14-15］同样针对强迫振荡，基于K 最近邻（Knearest neighbor，KNN）算法进行了振荡源定位的研究。文献［16］考虑广域电力系统数据传输的通信带宽限制，提出了基于自编码器的信号压缩与长短期记忆网络的振荡源定位方法。

然而，当前限制机器学习在振荡源定位领域应用的主要原因在于实际振荡数据的匮乏。机器学习是一种需要依赖大量高质量数据的数据驱动技术，但在实际电力系统中，相较于稳态数据，振荡数据极度匮乏。因此，实际系统振荡数据匮乏成为一个亟待解决的问题。迁移学习的发展为解决该问题提供了一个重要思路。文献［17-18］基于两种场景，利用迁移学习尝试解决次同步频段振荡数据匮乏的问题。通过调节仿真中系统控制参数以获得大量源域振荡样本，并将其迁移泛化至实际振荡领域。但上述研究并未考虑振荡分量的耦合特性。同时，随着系统规模的扩大及控制环节的复杂化，调节系统控制参数来形成大量的可迁移有效振荡样本也具有较大难度。此外，文献［18］所提迁移学习模型仅考虑了两域样本的全局边缘对齐，在两域差距较大时，迁移能力受限。

鉴于上述问题，本文针对直驱风电场接入弱交流系统引发次/超同步振荡的场景，提出一种新的基于深度子领域自适应的振荡源定位方法。首先，在仿真系统风机侧直接加入扰动源激发系统次/超同步频段强迫振荡以获取大量源域样本，源域数据集获取方式较为简单且容易实现。其次，利用迁移学习将源域泛化到实际系统次/超同步振荡领域，解决了实际振荡样本匮乏的问题。本文所用迁移算法考虑了颗粒度的对齐，相较于传统深度学习与迁移学习，特征泛化能力更强，在电力系统中具有更好的应用效果。最后，采用一个含直驱风机的电力系统仿真模型对所提定位方法进行了验证分析。结果表明，所提次/超同步振荡源定位方法可以在较短的时间内获得更为精确的定位结果。

1 深度子领域自适应

1.1 深度迁移学习

鉴于现代电网“双高”（即高比例可再生能源、高比例电力电子设备）的发展趋势，电力系统非线性化程度加剧，传统建模分析变得困难。同时，人工智能的快速发展为处理复杂的非线性问题提供了一种新的思路。由于人工智能本身依赖于大量数据积累，而实际电力系统中振荡数据匮乏，利用深度学习等进行数据驱动建模变得困难。迁移学习是一种将在具有较多数据样本的相似领域内学到的知识应用到相关领域，以解决该领域标签数据少、难以进行训练等问题的方法［19］。迁移学习的示意图如附录A 图A1 所示。本文基于迁移学习的优势，利用仿真系统中的强迫振荡域来学习实际振荡域的特征，以解决实际电力系统振荡数据匮乏的问题。

与传统深度学习不同，迁移学习具有两个数据域，分别为源域Ds和目标域Dt，下文用下标s 代表源域、t 代表目标域。源域具有大量标签样本，是需要迁移的对象，在本文中特指仿真系统形成的强迫振荡特征样本域。目标域即为缺乏标注样本，需要被给予迁移知识的对象，在本文中指实际系统振荡特征样本域。每个域都由样本空间X以及概率分布P(X)构成，即Ds={Xs，P(Xs)}，Dt={Xt，P(Xt)}。源域与目标域内的学习任务由标签空间与其对应的预测函数组成，记作T={Y，f}。在本文所提模型中，样本标签为引发次/超同步振荡的风机编号，预测函数即为定位振荡源的模型。其中，预测函数f本质为数据分布的条件概率Qs（Ys|Xs）、Qt（Yt|Xt）。当f为深度表征函数时即为深度迁移学习。在源域与目标域的数据特征完全相同的情况下，源域所学到的预测函数fs也可以完全泛化到目标域中，完成目标域的任务。但是，源域与目标域的初始数据特征是不同的，反映到数据上即两域的边缘分布和条件分布是不同的。因此，迁移学习的目标本质上就是解决两域的数据分布问题。为使所提出的振荡源定位方法具有适用性，不因样本权重的改变而导致适用性降低，本文采用基于特征的迁移学习方法。即通过模型的设计使得两域特征被映射到另一个潜在特征空间上，在该空间中，两域的特征分布完全一致，源域所学到的知识便可以完全泛化适应于目标域任务。

针对电力系统振荡样本极其匮乏的问题，本文将较易在仿真系统获得的强迫振荡样本构造成源域，将少量实际次/超同步振荡样本构造成目标域，构成迁移学习，从而解决振荡样本匮乏的问题，建立基于深度迁移学习的次/超同步振荡源定位模型

1.2 深度子领域自适应原理

加入扰动源所激发的强迫振荡与实际风机产生的次/超同步振荡在产生机理上就有着较大差异，导致两者产生的数据域也不尽相同，源域与目标域两域差异较大。当仅考虑数据域的全局领域自适应——两域边缘分布具有一致性，而忽略不同类别之间分布的差异性时，在源域与目标域相差较大的情况下，迁移效果具有局限性。鉴于此，本文提出采用深度子领域自适应的方法建立次/超同步振荡源定位模型。深度子领域自适应［20］的方法进一步考虑颗粒度的对齐（本文的颗粒度指不同的振荡源风机机组），通过利用颗粒度关系进行相关子领域对齐，使不同域的全局分布和局部分布同时被拉近。子领域自适应与全局领域自适应的区别如附录A图A2 所示。

在本文中，将仿真系统产生的强迫振荡所形成的源域记作Ds={（xs，1，ys，1），（xs，2，ys，2），… ，(xs，l，ys，l)}，源域为有标签数域，其中，l为源域的样本数，xs∈Xs、ys∈Ys分别表示源域样本与对应的标签。实际次/超同步振荡所形成的目标域记作Dt={xt，1，xt，2，…，xt，k}或Dt={（xt，1，yt，1），（xt，2，yt，2），…，（xt，m，yt，m），xt，m+1，xt，m+2，…，xt，k}，其为无标签或少量标签数域，其中，m为目标域有标签的少量样本个数，k为目标域的样本数量，xt∈Xt、yt∈Yt分别表示目标域中的样本和其对应标签。

深度子领域自适应的基本思想是通过在神经网络中设计不同适配层，进行两域相关子领域分布差异的测量，通过减小分布差异进而实现子领域的对齐。由此可知，子领域自适应的核心是设计适配层：通过选择合适的迁移正则项来量度两域之间分布的差异。在迁移学习中，最大均值差异（maximum mean discrepancy，MMD）是应用最为广泛的量度方式，但MMD 无法测量局部分布之间的欧氏距离，故在此基础上，进一步定义局部最大均值差异（local maximum mean discrepancy，LMMD），具体形式如下：

式中：p、q分别为源域和目标域的数据分布；Ec（·）表示类别c的数学期望；Ep，c（·）、Eq，c（·）分别表示类别c下源域和目标域数据的数学期望；H为再生核希尔伯特空间（reproducing kernel Hilbert space，RKHS）；ϕ(·)表示数据由原数据空间到RKHS 的映射。

设样本属于类别c的概率为ωi，c，本文中即表示该振荡样本溯源后振荡源为编号c风机的概率权重。定义ωi，c如下：

式中：xj、yj分别为域D中的样本及其对应标签，当公式用于计算源域样本权重时，D为Ds，当用于目标域时，D即为Dt；yj，c表示属于类别c的标签。

式中：b为标签类别总数，本文即为风机台数；ωs，i，c、ωt，j，c分别表示仿真系统强迫振荡所形成的源域样本xs，i与实际振荡形成的目标域样本xt，j溯源后振荡源为风机c的概率，其中，源域样本采用真实的标签ys，i来计算ωs，i，c，目标域样本采用模型预测的伪标签ŷt，j来进行ωt，j，c的计算，如果目标域中有部分真实标签，有标签部分以真实标签来进行参数的计算在理论上会提升迁移的效率。

通过加入概率权重，使用概率预测进行类别权重赋值，相较于直接使用模型预测伪标签［17］，会减轻标签错误时对模型性能的影响。

将式（3）展开后用于不同适配层来计算两域之间的距离，其函数如式（4）所示。

式中：o为适配层的层数；zs，i，o、zs，j，o分别为源域样本xs，i、xs，j在适配层o的高维激活向量；同理，zt，i，o、zt，j，o分别为目标域样本xt，i、xt，j在适配层o的高维激活向量；ns、nt分别为源域、目标域的样本数量；k（·）定义为映射的内积，定义式如式（5）所示。

综上所述，基于LMMD 的深度子领域自适应网络（deep subdomain adaptation network，DSAN）的数学架构可以表示为：

式中：Ω为适配层的集合；λ为迁移损失权重；第1 项J（·）表示分类损失，本文使用交叉熵函数计算分类损失；第2 项d̂o(p，q)即为使用LMMD 计算的自适应损失。

本文将该方法通过进一步适配于振荡源定位的场景，应用到实际含直驱风机系统次/超同步振荡源的在线定位。

2 基于DSAN 的次/超同步振荡源定位方法

2.1 源域与目标域样本空间构建

由第1 章分析可知，深度迁移学习的本质是对数据的特征进行泛化学习。与传统深度学习一致，样本特征的选择对于模型的准确率具有较大的影响。本章通过对源域与目标域样本特征的选择、样本数据处理等，完成源域与目标域样本空间的构建。

2.1.1 样本特征选择

本文研究所针对的直驱风机经弱交流电网并网的场景结构示意图如图1 所示。图中：V1，V2，…，Vb表示各台风机出口母线电压；Vp表示风电场并网母线电压；Va表示交流侧出口母线电压；P1，P2，…，Pb与Q1，Q2，…，Qb分别表示各台风机输出有功、无功功率；Xf1，Xf2，…，Xfb表示各风机侧电抗；R1、X1分别表示输电线路等效电阻和电抗；R2、X2分别表示交流侧等效电阻和电抗。直驱风电场用b台并联的直驱风机模型表示，汇集到集中母线上。经过弱交流系统连接并入交流主网（等效为无穷大系统）。风电场风机台数众多，当系统发生次/超同步振荡时，快速准确定位到振荡源风机对于振荡的平息至关重要。

图1 风机经弱交流系统并网场景示意图Fig.1 Schematic diagram of wind turbines connected to power grid via a weak AC system

为选取有效的数据特征，需研究电气量与振荡源之间的关系，选取与振荡源有关的电气特征。首先，根据闭环互联模型理论［21］，建立系统状态空间方程。

不考虑所研究风机外剩余子系统动态方程，风机子系统的系统状态空间方程为：

式中：ΔF1=［ΔV1，ΔI1］T为该风机子系统的输入变量，由风机子系统与剩余子系统并网处的电压和电流构成；ΔY1=［ΔP1，ΔQ1］T为所研究风机子系统的输出变量，即风机送出的功率；ΔX1为风机所有状态变量组成的列向量；A1、B1、C1、D1为风机子系统的系数矩阵。

不考虑风机子系统的动态方程，剩余子系统的系统状态空间方程为：

式中：ΔX2为剩余子系统的状态变量；A2、B2、C2、D2为剩余子系统的系数矩阵。

由式（7）、式（8）联立可知，风机经弱交流电网并网的互联系统状态方程如下：

式中：A为闭环系统的特征矩阵。

由传统的模式分析法可知［22］，当系统的线性化状态空间方程建立完成后，可以通过特征矩阵A计算系统的参与因子进而判断振荡源。参与因子的定义如式（10）所示。

式中：vμβ为右特征向量矩阵的第μ行第β列元素；wμβ为左特征向量的第μ行第β列元素；n为系统特征向量数。参与因子Cμβ衡量了受第μ个状态变量激励的情况下，第β个模式在该状态变量时域响应中的参与程度。

由式（10）可知，当已知闭环系统的特征矩阵A，便可以求出其参与因子C，即

式中：∂（·）表示参与因子与系统特征矩阵之间的映射关系函数。

联立式（7）—式（9）可知，在互联闭环系统中，闭环系统的特征矩阵A与系统的运行点M有关。因此，振荡源与系统电气量之间的关系可以表示为：

式中：S为振荡源标签，即风机标号；M由输入变量与输出变量构成，表示为M=［Y，F］=［P，Q，U，I］，其中，P、Q、U、I分别表示有功功率、无功功率、电压、电流；g（·）表示振荡源标签与系统参与因子之间的映射关系函数；h（·）表示系统特征矩阵与系统运行点之间的映射关系函数；s（·）表示振荡源标签与系统运行点之间的映射关系函数。

综上所述，实际系统振荡源与风机系统的有功功率、无功功率、电压、电流有关。同时，上述变量在实际系统中均能通过测量获得。显然，当利用数据驱动进行实际系统振荡溯源时，可选取风机出口母线处的有功功率、无功功率、电压、电流作为数据样本的特征。为形成同构迁移学习［19］，由强迫振荡所形成的源域亦采用风机出口母线处的有功功率、无功功率、电压、电流这4 个电气量作为源域样本特征。即本文所提振荡源定位方法两域样本特征均由各风机出口母线处的有功功率、无功功率、电压、电流构成。

2.1.2 样本生成与数据预处理

由上文分析可知，本文所提出的振荡源定位方法中，目标域样本集由少量的实际次/超同步振荡数据构成，源域样本集由仿真系统中加入扰动源生成的大量次/超同步强迫振荡数据构成。

1）目标域样本集构建

按照2.1.1 节所述，取实际系统次/超同步振荡时各风机出口母线电气量测的历史数据。选取样本所需的电气特征量：有功功率、无功功率以及A 相电压、电流，构建目标域样本，形成目标域样本集Xt。通过振荡历史记录或系统离线仿真分析的方法，获取少量历史振荡数据的真实溯源结果，形成目标域部分真实标签集Yt。进一步，对所获取样本集进行训练集和测试集的划分。

2）源域样本集构建

在根据实际电网场景案例搭建的时域仿真系统中，分别在不同的风机出口侧母线处注入谐波扰动，引发强迫振荡。所注入谐波频率为所对应的实际系统真实可以激发产生的次/超同步振荡频率。通过较大范围改变系统运行工况，在较宽频段内改变扰动源注入的谐波扰动分量，获取大量振荡数据。根据2.1.1 节可知，采集振荡时各个风机出口母线处的有功功率、无功功率以及A 相电压、电流波形数据构建源域样本，形成源域样本集Xs。并根据实际注入谐波扰动的风机母线所对应的风机编号形成源域标签集Ys。同理，对源域样本进行训练集与测试集的划分。

3）数据预处理

为加快后续神经网络梯度下降的速度，消除样本中特征量级不同对优化精度的影响［23］，利用minmax 归一化的方法，对所采集的样本数据进行数据预处理，将不同量级的P、Q、U、I特征都映射到［0，1］区间中。min-max 归一化的原理如式（13）所示。

式中：a为样本中不同特征的特征向量；a′为向量a经归一化后的特征向量。

2.2 次/超同步振荡源定位模型

由于实际电力系统次/超同步振荡数据匮乏，本文提出通过在仿真系统中激发强迫振荡，与实际系统次/超同步振荡构成迁移学习以解决振荡数据匮乏的问题。同时，由1.2 节可知，鉴于本文源域与目标域两域之间差异较大，本文采用考虑颗粒度对齐的迁移学习方法，即相关子领域自适应进行振荡源定位与识别研究［20］。

DSAN 的网络结构图如附录A 图A3 所示。由图可知，基于DSAN 的定位模型主要由特征提取器与适配层两部分组成。

基于次/超同步频段振荡样本的强非线性化数据特征，特征提取器采用具有强复杂特征提取能力的卷积神经网络（convolutional neural network，CNN），包括卷积层、激活层、池化层、全连接层等。由于电气振荡样本具有长条形的特点，特征矩阵维数较高，在训练过程中容易发生过拟合现象。因此，除去采用最大池化的方法（max-pooling）减少训练参数这一措施外，同时在模型中加入了Dropout 层来进一步防止过拟合。由2.1.2 节可知，归一化可以加快模型的收敛、提高模型的实用特性，因此，本文在对输入样本进行预处理的基础上，批归一化（batch normalization，BN）层的加入也在训练过程中对中间层进行再次归一化处理，提高模型的收敛性能。

通过2.1 节的分析可知，数据样本为次/超同步频段的有功功率、无功功率、电压、电流振荡曲线，相较于自然语言处理与计算机视觉领域，特征处理任务并不复杂。因此，本文在适配网络部分仅采用单层适配网络而非多层适配，提高了模型训练的速度。模型的网络结构与参数设置如表1 所示。

表1 模型网络结构与网络参数设置Table 1 Configuration of network structure and network parameter

2.3 次/超同步振荡源定位方法的具体流程

本文所提的次/超同步振荡源定位方法的具体实施流程如图2 所示。可以分为离线训练和在线应用两部分。

离线训练部分的具体步骤如下：

1）获取实际系统中次/超同步振荡历史录波数据，形成目标域样本集，对目标域数据进行预处理，划分形成目标域训练样本集与目标域测试样本集。

2）根据实际系统构建时域仿真系统，按照2.1.2节所述方式在仿真系统中激发强迫振荡生成源域样本，对源域数据进行预处理，划分形成源域训练样本集和源域测试样本集。

3）按照2.2 节DSAN 架构进行振荡源定位模型搭建。

4）利用两域训练集样本数据，通过多次尝试获取最优学习率等超参数，进行模型的训练。使用Iacc指标来衡量模型的准确率是否满足定位要求，设置Iacc初始设定阈值。Iacc定义如式（14）所示。

式中：N为测试集样本总数；Tc为预测与实际均是风机c为振荡源的测试样本数量，其中，c=1，2，…，b。

5）测试样本的Iacc未达到初始设定阈值时，根据系统损失函数按照梯度下降方式进行迭代，模型进行参数更新。

6）模型Iacc达到初始设定阈值时，停止训练并保存网络。此时，所获得的网络便是最终的次/超同步振荡源定位模型。

在线应用部分具体步骤如下：

1）根据量测设备获取系统待定位振荡源的在线次/超同步振荡量测数据。

2）利用本文2.1.2 节所提方式进行现场量测数据的数据处理，获得模型可用特征数据。

3）输入振荡源定位模型，获取振荡源位置标签，实现次/超同步振荡源在线定位。

3 算例分析

3.1 算例数据集的构建

本文将PSCAD/EMTDC 仿真软件中搭建的4 台直驱风机经弱交流电网并网的模型作为实验算例，进行所提方法有效性的验证，模型结构如附录B图B1 所示。模型搭建详细参数见附录B 表B1。

1）目标域样本获取：因无法获取实际系统振荡历史数据，本文采用搭建的仿真系统模拟实际系统产生少量目标域训练样本以及测试样本，进行所提振荡源定位方法有效性的验证。按照2.1 节样本空间构建的方法，设置4 个风电机组分别与交流系统耦合产生次/超同步振荡［24］，调节各机组的额定出力变化范围为0.5～1.0 p.u.，得到若干不同运行点以模拟实际系统运行情况。随着运行点改变，系统次/超同步振荡频率随之改变，变化范围为16～18 Hz、82～84 Hz。采集4 台风机出口母线处的有功功率、无功功率以及A 相电压、电流信号（采样频率为2 kHz，采样时长为0.5 s），形成目标域的振荡样本xt=［P1，Q1，U1，I1，P2，Q2，U2，I2，P3，Q3，U3，I3，P4，Q4，U4，I4］。剔除系统潮流不收敛的无效样本，经数据预处理后获取目标域有效训练样本400 个。同样，按照上述方法，获得有效测试样本364 个，并形成测试样本与少量训练样本的标签数据集Yt。

同时，在附录C 中给出了关于目标域样本数量选择对于模型准确度的影响，在附录D 中给出了关于样本数据长度对模型准确度的影响。通过上述研究，验证了本文所提定位模型在不同目标域构造（样本数量、数据长度）时的性能。

2）源域样本获取：在上述仿真模型中，分别在4 台风机出口侧母线处加入强迫振荡源，通过向系统注入周期性扰动（本算例中扰动频率为15～19 Hz、81～85 Hz），引发系统强迫振荡。改变风机出力情况（0.5～1），注入扰动幅值（0.01～0.06）来模拟实际运行中的若干运行点。根据2.1 节，记录振荡时各个风机出口母线处的有功功率、无功功率以及A 相电压、电流（采样频率为2 kHz，时长为0.5 s）形成源域样本xs=［P1，Q1，U1，I1，P2，Q2，U2，I2，P3，Q3，U3，I3，P4，Q4，U4，I4］，并按照2.1 节所示方法形成对应标签数据集Ys。剔除稳定、潮流不收敛等无效样本，经数据预处理后获得源域有效训练样本2 568 个，源域测试样本500 个。

经过上述样本生成过程，最终两域形成的样本数量如表2 所示。同时，在附录E 中，以一个样本生成为例，给出了样本中各个特征的时域仿真结果波形图。

表2 两域样本数量分布Table 2 Sample size distribution of two domains

3.2 模型训练结果

本文利用Python 语言在Facebook 公司发布的Pytorch1.7.0 架构搭建迁移学习网络，构建2.2 节所设计的振荡源定位模型，所采用计算机配置为12th Gen Intel®Core（TM） i5-12400。

在利用3.1 节产生的训练样本进行模型离线训练的过程中，样本分批次进行训练，批次大小设置为25，网络学习率与迁移损失权重分别设置为10-4与0.5。同时，采用Adam 加速算法进行模型训练的优化。

利用2.3 节所提出的评价指标Iacc来对模型的准确度进行评估，模型准确率随训练迭代次数变化的曲线如图3 所示。

图3 模型准确率随训练次数变化曲线Fig.3 Curves of model accuracy varying with training times

观察图3 曲线可知，随着训练的不断深入，模型的精准度虽有波动，但是整体呈现出逐渐升高的趋势。当训练次数达到300 次时，模型精确度已经达到较高水平，指标准确率达到90%以上，模型最终测试准确率为96.43%，基本可以满足实际应用中振荡源定位的精度要求。

为更加全面评估所提方法的性能，除准确率指标Iacc外，另定义每个类别的精准率Kc和召回率ςc再次对模型性能进行评估，定义如下：

式中：Fec为实际振荡源为风机e，但预测振荡源为风机c的样本数量；Fce为实际振荡源为风机c，但预测振荡源为风机e的样本数量。

模型混淆矩阵与指标评价结果如图4 所示，图中每个单元格中整数为样本数量，百分数为指标评价结果。模型对于每个类别的精准率以及召回率都能达到90%以上，模型定位在各个标签中表现都较为稳定。基本可以实现实际应用中振荡源的定位。

图4 定位模型的混淆矩阵Fig.4 Confusion matrix for localization model

进一步分析所提迁移学习方法的域适应效果，利用t-分布随机邻域嵌入（t-distributed stochastic neighbor embedding，t-SNE）算法，给出两域样本通过DSAN 前后的特征空间分布，如图5 所示。

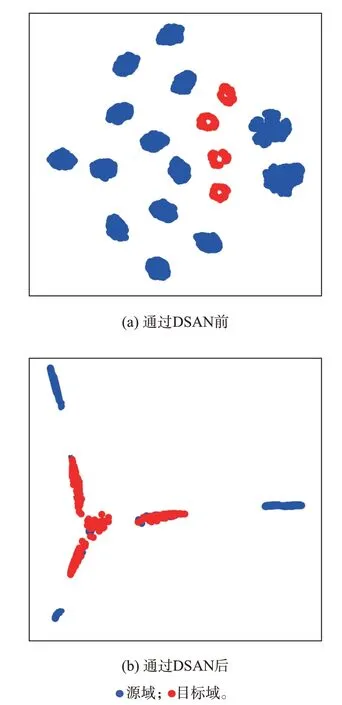
图5 DSAN 前后两域数据特征分布Fig.5 Distribution of data characteristics of two domains before and after DSAN

由图5 可以看出，在经过迁移学习网络之前，两域样本空间重合较少，分布差距较大；经过迁移学习网络后，两域分布趋势基本相同，数据映射到二维后空间分布基本重合，即两域此时的特征分布近似一致。上述过程表明，所搭建的DSAN 具有较强的领域自适应能力，完成了强迫振荡样本向实际系统次/超同步振荡样本的迁移泛化。

本文所提模型直接依托于数据特征信息进行振荡源的定位识别，因此，区别于传统基于机理的振荡源定位方法，模型不会随着振荡机理改变、振荡频带变宽而失效。为进一步验证本文所提振荡源定位方法在次/超同步较宽频段内的适应性，针对系统存在不同频段次/超同步振荡的情况进行了仿真验证，具体仿真实验过程与结果见附录F。实验结果表明，本文模型在次/超同步宽频带内都具有较高的模型精准度及适应性。

进一步，在附录G 中给出了算例规模扩大时模型定位性能的验证。验证结果表明，本文所提振荡源定位模型不会随风机台数增加而失效，仍具有较高的定位精度。

综上，通过算例验证可以说明，本文所提的振荡源定位方法初步解决了实际系统次/超同步振荡数据匮乏的问题，具有较高的精准度，基本可以满足在线应用的需求。

3.3 不同振荡源定位方法的对比

3.3.1 本文所提定位模型与传统深度学习定位模型的对比

为了进一步测试本文所提方法在两数据域差距较大时的领域自适应能力，本节基于卷积神经网络设计针对强迫振荡的深度学习定位模型，将其直接用于实际振荡定位中。模型结构如附录A 图A4 所示，同时，在网络中额外加入了Dropout 层用于防止模型的过拟合。

利用源域中强迫振荡的数据进行定位模型的训练，当源域的测试精度达到100%时，目标域测试精度只有52.74%。即未经过迁移的情况下，源域与目标域的数据分布差异是较大的，源域所训练的定位模型并不可以直接用于目标域中。同样，仿真系统中强迫振荡样本并不可以直接扩充实际振荡样本集。而本文提出通过子领域自适应方法，进行两域的特征迁移，最终定位模型的准确度可达到96.43%。两种定位模型的对比可以表明：由于两种振荡特征差距较大，利用仿真系统强迫振荡所训练获得的振荡源定位模型，无法直接用于实际次/超同步振荡源定位。进行两域之间的迁移学习是利用仿真系统中的强迫振荡来解决实际振荡数据缺失的必要选择。

3.3.2 本文所提定位模型与基于对抗迁移的定位模型的对比

域对抗神经网络（domain-adversarial neural network，DANN）将深度学习中对抗生成网络的对抗思想引入迁移学习中，是目前常用的一种基于特征的迁移学习方法［25］。该方法将网络主要分为特征提取器、标签分类器以及域判别器。该方法通过不断优化网络参数，使域判别器无法正确分辨出数据的域来源，以此来获得域不变特征。本文尝试基于该方法进行强迫振荡与实际次/超同步振荡之间的迁移，构建的振荡源定位模型基本架构如附录A图A5 所示。

为防止模型过拟合，在网络中也额外加入了Dropout 层。模型准确率曲线与本文所提模型准确率曲线对比如图6 所示。

图6 DANN 与DSAN 的准确率对比Fig.6 Accuracy comparison of DANN and DSAN

如图6 所示，当训练次数达到300 次时，本文所提模型准确度基本稳定在90%以上，而基于DANN的振荡源定位模型精度仍处于较低水平。为防止DANN 训练不充分导致模型准确度较低，继续对模型进行训练，当训练次数大于1 000 次时，模型基本收敛，保留其最优模型，其模型精度与本文所提方法的模型精度测试结果对比如表3 所示。

表3 基于DANN 和DSAN 模型的测试结果Table 3 Test results based on DANN and DSAN models

由表3 可知，基于DANN 的振荡源定位模型在训练次数达到1 000 次时，其最高准确率仅为85.44%，准确度远低于本文所提定位模型。且与本文所提的基于DSAN 的振荡源定位方法相比较，其训练收敛速度也较慢。同时，在训练过程中，由于对抗网络的存在，DANN 的训练难度远大于DSAN。综上可知，基于DANN 的振荡源定位模型在实际电力系统振荡源定位的在线应用中适应性不强。而本文所提振荡源定位方法在训练收敛难易程度、收敛速度以及模型准确率上，相较于基于对抗的迁移定位模型存在着较大优势。

4 结语

本文针对直驱风机经弱交流电网并网的场景，提出了一种基于深度子领域自适应的次/超同步振荡源定位方法，并给出了振荡源定位方法的具体实现过程。通过将仿真系统中的强迫振荡迁移到实际次/超同步振荡领域，完成实际风机系统次/超同步振荡源的定位。最后，设计了直驱风机经弱交流系统并网的仿真算例，验证了所提方法的有效性与优越性，并得出以下结论：

1）本文将仿真系统中获取的强迫振荡样本迁移到实际次/超同步振荡领域中，初步解决了实际系统振荡数据匮乏、获取困难的问题。相较于其他源域的选择方法，本文提出将仿真系统中利用周期性强迫源激发的系统强迫振荡作为源域样本，使得样本数据获取更加简单。该方法为由于振荡数据匮乏导致机器学习在振荡领域发展受限的问题提供了一种解决思路。

2）通过算例分析可知，本文所使用的迁移方法相较于其余基于特征的迁移学习方法，在训练难易程度、模型收敛速度以及定位准确度上都有着较大的优越性，模型的可塑性较强。

3）本文所提的振荡源定位方法不需要进行复杂的机理建模，不依赖于数学模型的精度，在定位速度、准确度上相较于传统振荡源定位方法有着较大的优势。实现了离线训练、在线应用，推动了智能电网的建设和发展。

基于本文当前工作，未来可研究本文所提方法在高频领域的应用，以建立全频段振荡源在线定位模型。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。