不同核函数高斯过程回归算法与不同因子输入情况下对长江流域蒸散发量应用研究

2023-09-15杨梓涵崔峥铮张鹏程

水利科技与经济 2023年9期

杨梓涵,崔峥铮,张鹏程

(河海大学水文水资源学院,南京 210024)

0 引言

参考作物腾发量(Reference evapotranspiration,ET0)是自然界水分循环与能量平衡的重要组成部分,与降水等因素共同影响着区域的干湿状况,也是估算生态需水和农业灌溉用水的关键因子[1]。长江流域地处亚热带季风气候区,年降水量大,流域内有丰富的自然资源,是我国重要的水利经济带。因此,对长江流域内部分城市的参考作物腾发量进行研究,对水资源合理开发利用与水循环有促进和指导意义。

目前,常用的参考作物腾发量估算公式主要有Penman-Monteith、Priestley-Taylor、Hargreaves-Samani和Thornthwaite 公式[2],这4个公式对长江流域都具有一定的适用性。由于每个公式计算因子不同,对不同地区蒸散发计算的结果精度也不同,许多学者针对不同地区对ET0估算公式进行了适用性分析并进行修正改进。如黄强等[2]针对珠江流域42个观测站点1959-2011年的逐日气象数据,以实测蒸散发数据为基准,探讨了PM公式、PT公式、HS公式和TH公式在珠江流域蒸散发计算中的适用性,结果表明PM公式在不同季节和地区的计算结果都较为稳定,与实测值更接近,最适用于珠江流域的蒸散发计算。朱潇枭等[3]针对海南省7个气象站点2000-2014年的逐日气象数据,以PM公式计算结果为标准,对Priestley-Taylor法,Irmak-Allen法和Hargreaves-Samani法的适用性进行了评价和对比分析,结果表明3种不同的ET0计算方法在海南省的相关性依次为:PT公式>IA公式>HS公式。

ET0的计算可以看作是一个依赖于大量气象变量的复杂非线性回归过程。因此,很难建立准确的经验模型来代表所有复杂的过程[4]。近年来,有学者提出ET0估计的机器学习方法,因为它们可以为非线性和多变量函数提供简单的解决方案[5]。FAN等[4]基于我国不同气候区8个气象站点1960-2010的逐日气象数据,对SVM、ELM、RF、M5tree、GBDT、XGBoost这6种高斯过程回归算法模拟ET0的精度进行了对比,结果表明GBDT和XGBoost在模拟ET0中有着显著的优越性,但SVM和ELM是模拟ET0最稳定的两个模型。赵文刚等[6]选取BP神经网络、极限学习法和小波神经网络3种较为常用的机器学习法,以广东省典型代表站点1981-2010年的实测逐日气象数据为研究对象,对比了3种高斯过程回归算法的可靠性,结果表明ET0计算精度表现为:BP>极限学习机>小波神经网络。此外,还有部分学者针对有限气象数据条件下高斯过程回归算法计算ET0的精度进行了研究[7-8]。

因此,本文以长江流域10个站点1970-2019共50年的逐日气象数据为研究对象,以PM公式计算的ET0为参考值,对比不同因子输入组合情况下,采用PT公式、HS公式、TH公式和3种不同核函数的GPR算法为计算方法,计算逐日参考作物腾发量的精度。本研究目的:①对比全气象因子输入情况下,3种ET0经验公式与3种不同核函数的GPR算法计算参考作物腾发量的计算精度。②对比不同因子输入情况下,3种不同核函数GPR算法的计算精度,并尝试分析因子输入改变情况下计算精度改变的原因。

1 材料与方法

1.1 数据资料

本研究所使用的气象资料由国家气象科学中心(http://www.nmic.cn/)提供。基于站点空间分布均匀且具有较强代表性为原则,收集了长江流域10个常规气象站近50年(1970-2019)的逐日气象数据,主要包括最低气温(Tmin,℃)、最高气温(Tmax,℃)、平均气温(Tmean,℃)、相对湿度(RH,%)、平均本站气压(P,kPa)、日照时数(N,h)、风速(U2,m/s)共8项指标。

1.2 参考作物腾发量(ET0)计算方法

1.2.1 FAO-56 Penman-Monteith模型

由于FAO-56 PM公式计算精度较高,能够较为准确反映参考作物腾发量的真实情况,因此近年来一直被广泛应用。具体计算公式如下:

(1)

式中:Rn为到达地表的净辐射,MJ/(m2·d);Tmean为日平均气温,℃;G为土壤热通量,MJ/(m2·d);γ为干湿计常数,kPa/℃;es、ea分别为饱和水汽压与实际水汽压,kPa;Δ为饱和水汽压与温度曲线的斜率,kPa/℃;U2为距离地面2m处的日平均风速,m/s。

1.2.2 Hargreaves-Samani模型

HS公式是一种基于温度来估算ET0的方法,由于需要的气象数据较少,常用于气象设备缺乏地区的ET0预报。其表达式为:

(2)

式中:Ra为大气辐射,MJ/(m2·d);C、E、T为Hargreaves公式的3个参数,建议值分别为0.0023、0.5和17.8。

1.2.3 Priestley-Taylor模型

Priestley-Taylor(P-T)公式法是在假定周围湿润的条件下提出来的,因此该方法一般适用于在湿润地区计算参考作物腾发量。其公式如下:

(3)

式中:α系数主要考虑空气动力因素影响,一般情况下取1.26;λ=2.501-0.002361T或直接取2.45。

1.2.4 Irmak-Allen模型

Irmak-Allen(I-A)见式(6):

ET0=0.489+0.289Rn+0.023Tmean

(4)

1.3 高斯过程回归算法

1.3.1 高斯过程回归(GPR)

高斯过程回归(GPR)数学模型是依赖于非参数核的概率模型,它在机器学习编程领域具有重要意义[9]。

假设GPR模型中输入向量(x)和目标(y)之间的运算关系为:

yi=f(xi)+ε

(5)

式中:f(xi)为任意函数;ε为噪声(回归残差)。

本研究中,认定各选定的气候指标为输入向量,参考作物腾发量为输出向量。

在函数f(x)中,f是因变量,x为自变量,并且任何未观察到的数对(x*,f*)见式(6)。

(6)

式中:K(X,X) 为训练数据中所有点之间的n×n协方差矩阵;k(X,x*) 为点x*和训练数据之间的n×1协方差向量。

p(f*|x*,X,f)=N(k(x*,X)K(X,X)-1f,k(x*,x*)-k(x*,X)K(X,X)-1k(X,x*))

(7)

(6)式通过最大化f*条件下的联合概率来确定f*。为了利用有噪声的数据,该模型必须伴随有测量误差。因此,式(5)常常被改为如下形式:

(8)

条件似然函数变化为:

方差变化为:

式中:σ2为观测误差的方差;I为单位矩阵。

本文研究中运用的3种核函数如下:

1)二次有理核函数。公式为:

(9)

2) 平方指数协方差函数(SE)。公式为:

(10)

3)Matern协方差函数(Matern 5/2)。公式为:

(11)

式中:Kv为修正贝塞尔函数。

1.3.2 评价方法

ET0精度采用平均绝对误差(MAE)、均方根误差(RMSE)和决定系数R2这3个指标进行评价[10],各指标的计算公式为:

(12)

(13)

(14)

通常情况下,MAE和RMSE越小,表明模型偏差越小,精度越高;R2越接近1,表明模型的拟合程度越高。

1.4 统计与分析

使用Microsoft Excel 2011对各站点气象数据进行整理,并采用FAO56-PM公式、HS公式、Priestley-Taylor公式和Irmak-Allen公式对ET0进行计算,采用Matlab 2021b对机器学习进行训练与预测,并采用Origin 2021对3种经典算法和3种高斯过程回归算法的预测精度进行图表绘制。

2 结果与分析

2.1 基于灰色关联分析法分析不同气象因子对逐日蒸散发的影响程度

灰色关联分析法是一种根据因素之间发展趋势的相似或者相异程度,即“灰色关联度”,作为用来衡量因素间的关联程度的一种方法。

对ET0影响程度排序为:日最高气温>平均气温>日最低气温>平均本站气压>平均风速>相对湿度>日照时数,将关联度数据进行可视化,见图1。

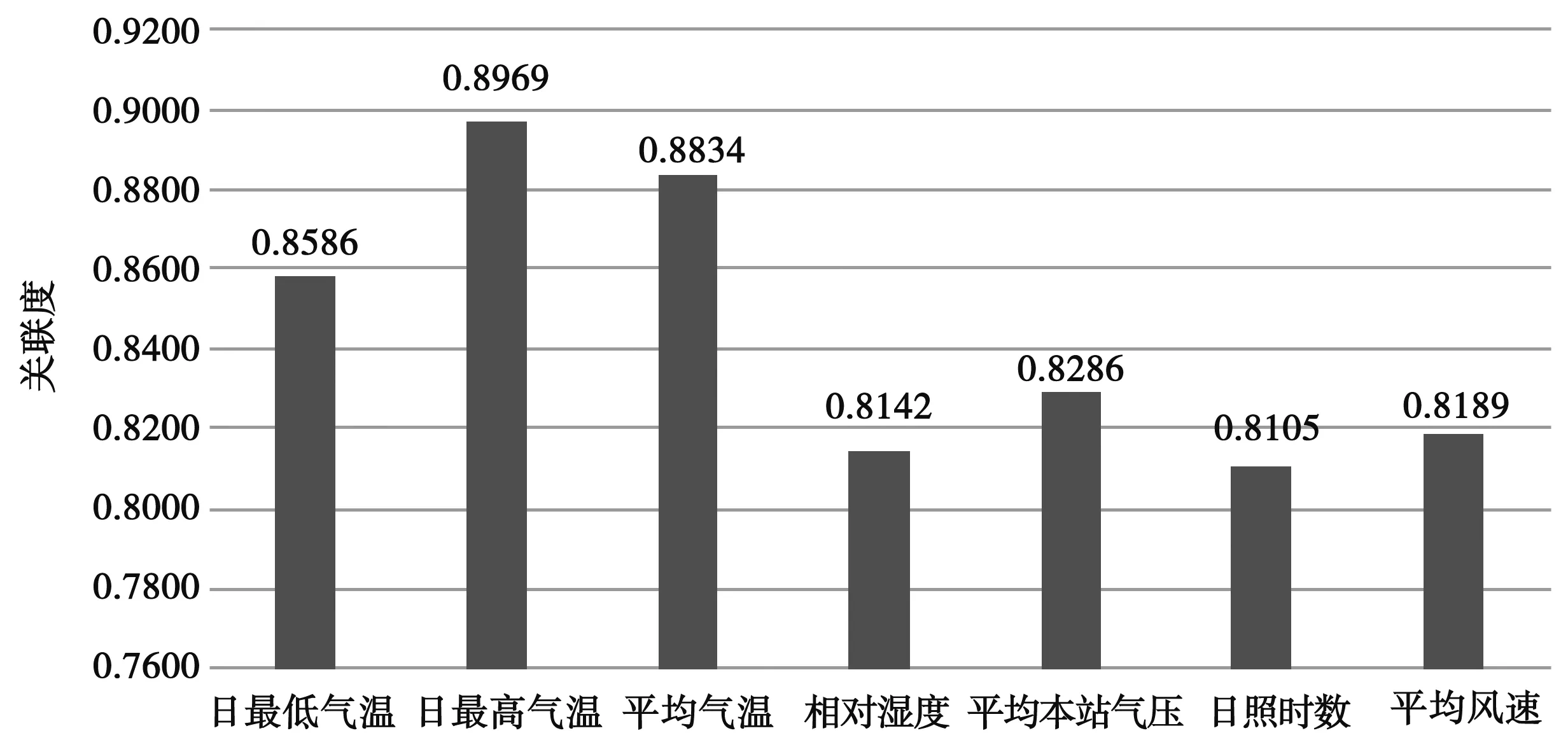
图1 关联度可视化

利用灰色关联度分析可得,日最高温度对ET0影响较大,日照时数对ET0影响较小,其余子因素对ET0的影响适中。

2.2 基于同一参考公式全因子输入下的3种经典算法和3种不同核函数高斯过程回归算法预测精度对比

为了比较Hargreaves-Samani、Priestley-Taylor、Irmak-Allen等3种经典算法和二次有理、平方指数、Matern 5/2等3种不同核函数高斯过程回归算法在全因子输入下预测ET0方面的精度情况,本研究首先通过PM公式、HS公式、Priestley-Taylor公式和Irmak-Allen公式,计算出各站点逐日参考作物腾发量ET0,PM、ET0,HS、ET0,PT、ET0,IA,再分别以前40年(1970-2009年)逐日气象资料(Tmin、Tmax、Tmean、RH、P、N和U2)和ET0值(ET0,PM)为机器学习输入变量和输出训练集,并最终通过输入后10年(2010-2019)逐日气象因子,模拟该时间序列上的ET0值,最后与对应的ET0,PM值进行对比分析,其具体结果见图2。

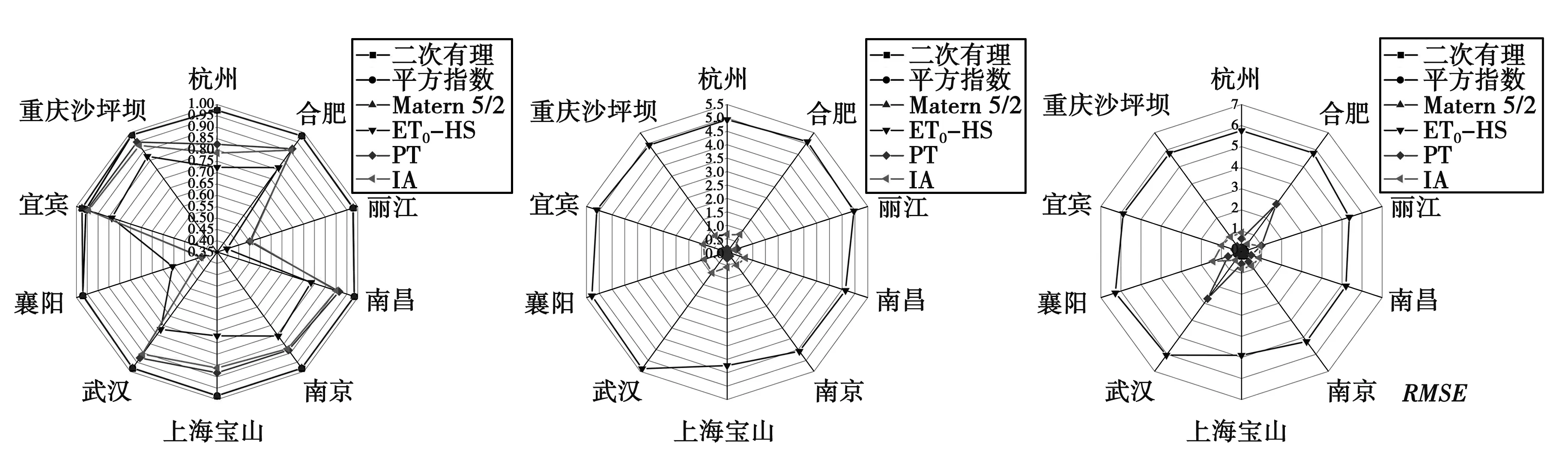
图2 PM参考公式下3种经典算法和3种不同核函数高斯过程回归算法评价指标对比

由图2可以看出,当以PM公式计算的ET0结果为参考时,Hargreaves-Samani公式计算结果的R2、MAE和RMSE分别维持在0.396～0.871、4.235～5.378和4.900～6.279范围内;Priestley-Taylor公式计算结果的R2、MAE和RMSE分别维持在0.422～0.951、0.017～0.396和0.348～2.805范围内;Irmak-Allen公式计算结果的R2、MAE和RMSE分别维持在0.424～0.945、0.284～0.952和0.472～1.419范围内。二次有理核函数模拟结果的决定系数R2的变化范围为0.970～0.988,MAE的变化范围为0.003～0.105,RMSE的变化范围为0.172～0.232;平方指数核函数模拟结果的决定系数R2的变化范围为0.957～0.988,MAE的变化范围为0.002～0.105,RMSE的变化范围为0.172～0.269;Matern 5/2核函数模拟结果的决定系数R2的变化范围为0.970～0.988,MAE的变化范围为0.001～0.103,RMSE的变化范围为0.171～0.233。

从整体上分析可以得到,在以PM为参考公式情况下,6种算法的模拟ET0表现效果均为:Matern 5/2>二次有理>平方指数>PT>IA>HS,总体上3种不同核函数高斯过程回归算法的预测精度远优于3种经典算法。

2.3 基于同一参考公式不同因子输入下的3种不同核函数高斯过程回归算法预测精度对比

为了比较二次有理、平方指数、Matern 5/2等3种不同核函数高斯过程回归算法在不同因子输入下预测ET0方面的精度情况,本研究首先通过PM公式计算出各站点逐日参考作物腾发量ET0,PM,再根据2.1一节灰色关联分析结果,确定四因子、五因子、六因子3种因子输入组合。四因子输入时,分别以前40年(1970-2009年)逐日气象资料(Tmin、Tmax、Tmean和P)和ET0值(ET0,PS)作为机器学习输入变量和输出训练集;五因子输入时,分别以前40年(1970-2009年)逐日气象资料(Tmin、Tmax、Tmean、P和N)和ET0值(ET0,PM)作为机器学习输入变量和输出训练集;六因子输入时,分别以前40年(1970-2009年)逐日气象资料(Tmin、Tmax、Tmean、P、N和U2)和ET0值(ET0,PS)作为机器学习输入变量和输出训练集,并最终通过输入后10年(2010-2019)逐日气象因子,模拟该时间序列上的ET0值,最后与对应的ET0,PM值进行对比分析。具体结果见图3。

由图3可以看出,当以PM公式计算的ET0结果为参考时,二次有理核函数在四因子输入下模拟结果的R2、MAE和RMSE分别维持在0.569～0.932、0.025～0.182和0.407～0.869范围内;二次有理核函数在五因子输入下模拟结果的R2、MAE和RMSE分别维持在0.804～0.963、0.011～0.117和0.303～0.560范围内;二次有理核函数在六因子输入下模拟结果R2、MAE和RMSE分别维持在0.908～0.977、0.027～0.202和0.055～0.454范围内。

当以PM公式计算的ET0结果为参考时,平方指数核函数在四因子输入下模拟结果的决定系数R2的变化范围为0.568～0.932,MAE的变化范围为0.026～0.181,RMSE的变化范围为0.407～0.870;平方指数核函数在五因子输入下模拟结果的决定系数R2的变化范围为0.801～0.963,MAE的变化范围为0.011～0.120,RMSE的变化范围为0.303～0.565;平方指数核函数在六因子输入下模拟结果的决定系数R2的变化范围为0.910～0.976,MAE的变化范围为0.028～0.202,RMSE的变化范围为0.252～0.453。

当以PM公式计算的ET0结果为参考时,Matern 5/2核函数在四因子输入下模拟结果的决定系数R2的变化范围为0.569～0.932,MAE的变化范围为0.028～0.182,RMSE的变化范围为0.406～0.868;Matern 5/2核函数在五因子输入下模拟结果的决定系数R2的变化范围为0.803～0.963,MAE的变化范围为0.011～0.118,RMSE的变化范围为0.303～0.561;Matern 5/2核函数在六因子输入下模拟结果的决定系数R2的变化范围为0.909～0.977,MAE的变化范围为0.026～0.201,RMSE的变化范围为0.251～0.453。

从整体上分析可以得到,在以PM为参考公式的情况下,3种不同核函数高斯过程回归算法的模拟ET0表现效果均为:六因子>五因子>四因子。

3 讨论与分析

3.1 经典算法和机器学习算法适用性对比

不同经典算法对ET0的计算结果有显著不同,同样不同机器学习算法对ET0预测结果有显著影响。如任传栋等[10]以山东省为研究区域,选取深度神经网络(DNN)、时间卷积神经网络(TCN)和长短期记忆神经网络(LSTM) 3种深度学习模型,极限学习机模型(ELM)、广义回归神经网络模型(GRNN)和随机森林模型(RF) 3种传统机器学习模型,Hargreaves-Samani模型(HS)、Droogres-Allen模型(DA)、Priestley-Tayor模型(PT)、Marrink模型(MK)、WMO模型(WMO)、Trabert模型(TRA) 6种经验模型,以均方根误差(RMSE)、决定系数(R2)、平均绝对误差(MAE)和效率系数(Ens)为精度评价体系,找出了适用于山东省ET0估算的最优模型,结果表明,相同气象参数输入条件下,机器学习模型精度普遍优于经验模型。李可利[11]以陕西省为研究区域,利用陕西省30个气象站点(1960-2016年)逐日气象资料,采用FAO P-M公式计算出标准ET0,对ET0进行时空分布特征分析、敏感性分析,并对ET0进行周期分析、预测,对ANFIS、RF、SVM 3种机器学习算法在陕西省ET0计算的适用性与可移植性进行分析,结果表明,在使用相同气象因子计算ET0时,SVM模型要优于H-S、Iramk、Makkink、P-T等4种传统ET0计算方法,SVM可以应用于陕西省缺少气象资料地区的ET0计算,代替其他ET0简化方法,提高计算精度。上述研究成果与本研究的结果保持一致。高斯过程回归的本质是通过一个映射把自变量从低维空间映射到高维空间的过程,由于选择核函数与惩罚参数的不同,该模型的预测精度也不同,所以该模型存在着一定的优化空间,有待进一步深入研究。