基于支持向量机回归算法陕西省降水量空间插值研究
2023-09-15樊庆
樊 庆
(榆林水文水资源勘测中心,陕西 榆林 719000)
降水量是雨量学中一个非常关键指标,对气候变化、水资源管理以及农业生产等方面都有着重要作用[1-3]。因此,精确预测和插值降水量的空间栅格面,对于降水状况的监测和预报具有重要的实践意义。经典降水量插值局限于Anusplin、Oridinary kriging、Inverse Distance Weighting等[2-5],其基于线性关系假设,而只能反映局部站点尺度降水数量信息,无法准确解释空间尺度连续性分布特征。支持向量机回归模型(Support Vector Machine Regression, SVMR)是一种非参数回归方法,通过寻找最优超平面,使多维数据拟合收敛[6-7]。相比于其他插值方法,SVMR具有更好的稳健性和泛化能力,可以有效处理高维数据和非线性问题。
本文基于SVR模型,对陕西省降水量进行空间插值,旨在全面探究其应用性,为雨量灾害预报、水资源管理、农业生产等领域的相关决策提供科学依据。
1 研究区与数据资料介绍
陕西省位于我国地理中心,介于N31°42′-N39°35′、E105°29′-E111°15′,总面积20.56×104km2。受地形环境、海陆位置、季风影响,由北向南依次为温带大陆性季风、亚热带季风气候,分属中温带半湿润区和湿润区,多年平均气温6℃~13℃,降水量分布范围300~1 100mm,无霜期180~240d,日照时数2 300~2 600h,积温一般为1 500℃~4 200℃,气候资源呈由南向北减少。境内为陕北黄土高原、关中盆地和陕南秦巴山地分异地貌,海拔320~3 780m,植被呈地带性分异,其中优势物种为马尾松、毛竹、刺槐等。区域分属长江、黄河流域,流域面积占比分别为35.37%、36.82%,另有27.81%属内流区。
所使用的雨量降水资料从国家气象科学数据中心共享获取。共收集到研究区2001-2020年92个雨量站点逐日降水量资料(图1),各站点不存在数据缺失。将原站点雨量数据在Excel 2016中进行处理,先合成逐年数据,再计算得到近20年来平均值。
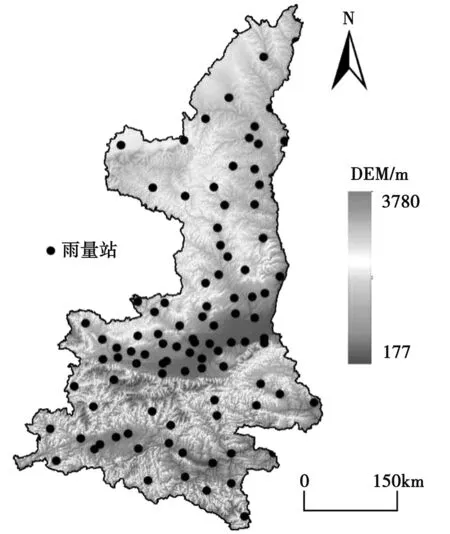
图1 研究区地形和雨量站点分布
2 支持向量机回归插值方法
2.1 支持向量机回归原理
SVR是一种用于建立连续变量之间非线性关系的机器学习算法。与其他回归方法不同的是,支持向量机回归通过在数据集中找到一条最优曲线或者超平面,即最小化训练误差和最大化有效边缘来进行回归。支持向量机回归的亮点在于其通过使用核函数来处理非线性问题,使输入样本更容易进行分离。对于训练数据集为D={(xi,yi)},xi是n维向量,yi是标量预测值,引入松弛变量ξi和ξi*,最小化如下的目标函数:
(1)
式中:C为惩罚系数;w、b分别为模型的系数和截距。
通常引入的核函数有高斯核、多项式核和Sigmoid核函数,本文选用高斯核函数进行建模,公式如下:
K(xi,xj)=exp(-‖xi-xj‖2)/(2σ2)
(2)
式中:σ为超参数[6-7]。
2.2 基于支持向量机的降雨量插值流程
1)数据预处理。将获取的研究区DEM、NDVI数据重采样成100m空间分辨率,设置其投影系统为UTM-CGS-1984,并利用处理后DEM栅格单元中心生成其地理经度(Lon)、地理纬度(Lat)的栅格面数据,由此构建环境变量栅格数据集,其包含DEM、NDVI、Lon和LAT等。再利用ArcGIS的Spatial Analysis→Extract→Extract multi-value to points工具,提取92个雨量站点位置所对应的环境变量信息,进而构建样本集。
2)SVR模型训练。按照7∶3的比例随机划分训练集合测试集,前者用以构建SVR模型,模型中因变量为站点降水量值,自变量为环境变量值,利用Rstudio软件中的caret和e1071程序包设计SVR模型,并通过grid search方法对模型中关键参数Cost、Sigma进行寻优。
3)空间插值预测。将构建的SVR模型代入环境变量栅格数据集进行空间预测,生成研究区100m空间分辨率的降水量栅格图。
4)插值精度验证。以测试集中的因变量为真值,提取相应站点位置对应的预测值,进而计算二者之间的决定系数R2、平均相对误差MAE、均方根误差RMSE,用以评价SVR模型的插值精度。公式如下:
(3)
(4)
(5)
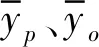
为证明SVR算法优势,以传统的Ordinary Kriging(OK)、Inverse Distance Weighting(IDW)算法为对照模型。
3 结果与分析
3.1 陕西省雨量站点数据统计特征
针对每一站点降水量,统计其近20年来降水量平均值,然后计算空间92个站点降水量统计特征,见表1。由表1可知,研究区站点降水量最大值为陕南镇巴站的1 317.55mm,最低值为陕北三原的353.39 mm,最大最小相差964.16mm,其统计平均值641.33mm,中值593.90mm,离差系数0.30,表明研究区降水量空间分异性强烈。进一步统计表明,其中有54个站点观测的径流量低于全域平均值,仅34个站点达到平均值以上,表明该站点观测值呈非平稳分布。因此,利用自然对数变换,使其符合正态分布形式,得到其Pks值<0.05。

表1 研究区雨量站点降雨量统计特征
3.2 支持向量机回归模型建立
本研究选择径向基函数(Radial Basis Function, RBF)作为核函数,设计基于R语言设计SVR模型关键代码如下:

train_index <- sample(1:nrow(data), round(nrow(data) ∗ 0.7)) # 70%的数据用于训练traindata <- data[trainindex, ]testdata <- data[-trainindex, ]tunegrid <- expand.grid(Cost = seq(0.1,1,0.1), Sigma= seq(0.001,0.1,0.001))svrmodel<- train (y~NDVI+DEM+Lon+Lat,data = traindata, method= ′svmRadial′, metric = "MAE" ,tuneGrid = tunegrid, trControl = control)#超参数优化predicted <- predict(svmmodel1,traindata[,-1])R2<-cor(predicted, testdata[,-1])^2MAE<-mae(predicted, testdata[,-1])RMSE<-(predicted, testdata[,-1])##精度评估
SVR模型性能不仅受数据结构影响,还对超参数的配置敏感。利用grid search方法,先对参数设置搜索空间,其中Cost的空间为[0.1,1],Sigma为[0,0.1],其迭代步长分别为0.1和0.01。经较差验证发现,当超参数Cost、Sigma取值分别为0.3、0.016时模型的MAE达到最小,仅为86.5mm。SVR拟合过程的鲁棒性和准确性见图2。
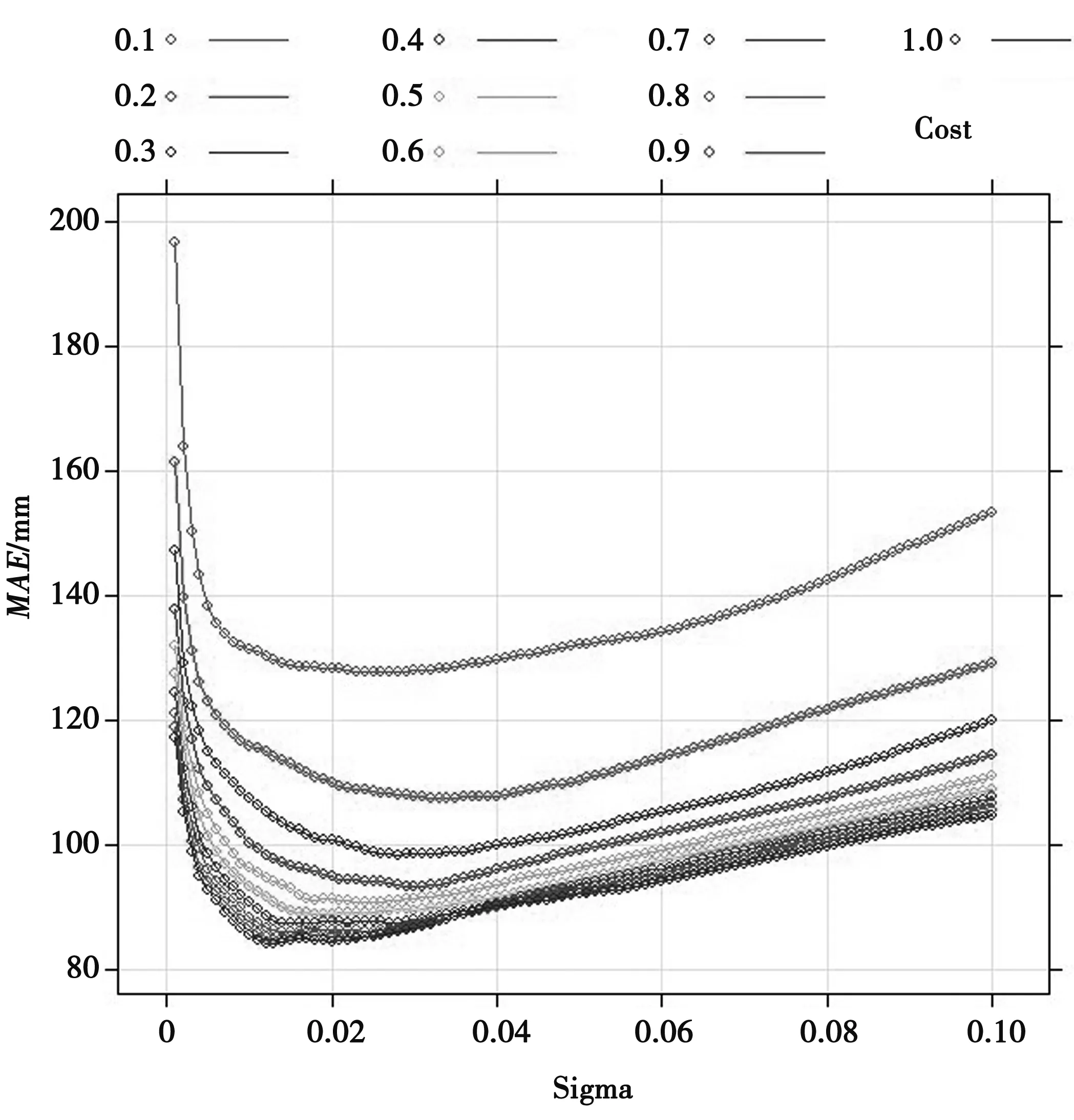
图2 SVR模型参数优化过程图
3.3 基于支持向量机回归模型降水量空间插值结果
通过对降水量数据的处理和SVMR模型的拟合,得到陕西省降水量的空间插值图,见图3。图3显示,降水量分布范围343~1 254mm,空间平均值658mm,这与站点统计值接近。降水量最高值分布于陕南,局部可达1 100~1 300mm;关中地区次之,介于550~700mm之间;陕北地区最少,仅为343~500mm。表明研究区降水量呈现自南向北地带性减少分布特征,这与研究区实际情况一致。另外,图3呈现局地降水量随地形分布的规律,并且精细刻画出局部渐变。综合而言,该降水量分布图具有科学性、可靠性。

图3 基于SVR算法陕西省降水量空间插值分布图
3.4 支持向量回归插值法精度分析
利用28个站点降水量进行独立验证,真实降水量值与不同算法的插值结果散点图见图4。由图4可知,SVR模型中散点图聚集性较好,离散性较低,其中R2为0.71,MAE和RMSE分别为108.43、128.39mm。对照模型中的OK插值法精度参数R2为0.62,MAE和RMSE分别为129.54、143.39mm;而IDW插值精度R2更低,仅为0.59,MAE和RMSE为118.45、152.16mm,且其离散性更大。
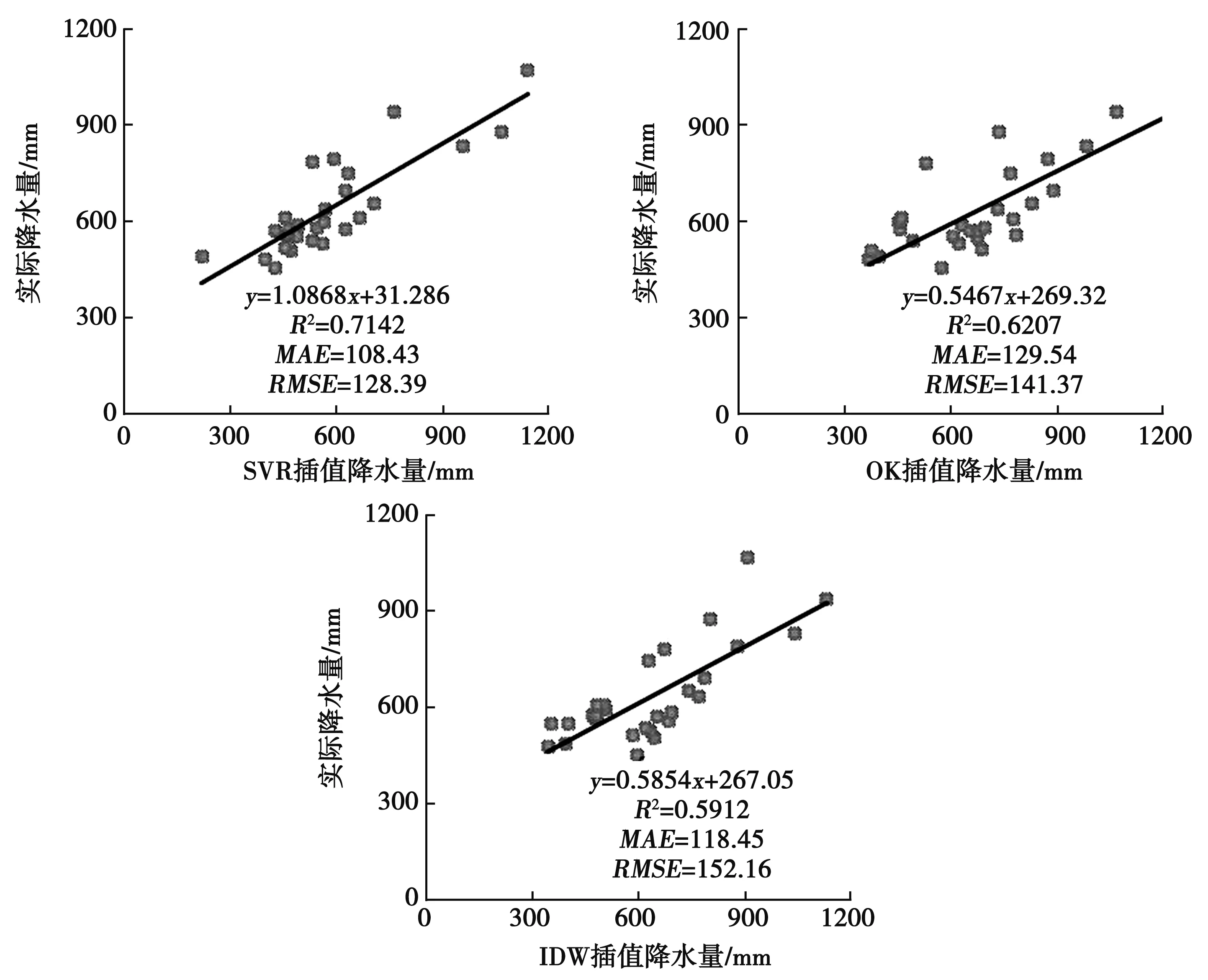
图4 不同算法对降水量进行空间插值的精度比较
由此可见,SVR模型插值精度更高,这归因于其能拟合降水量分布与不同环境变量之间非线性关系。相比于OK和IDW模型的R2增加14.52%、20.34%;MAE降低16.30%、8.46%,RMSE减小9.18%、15.62%,表明SVR插值法在研究区降水量空间预测性插值具有良好应用能力。
4 结 论
随着气候变化的加剧,雨量科学越来越受到人们的关注。在雨量科学领域,降水量的空间插值是雨量预报、环境保护等经常用到的一种技术。本文引入SVR算法,改进陕西省降水量空间插值精度,结论如下:
1)SVMR模型通过良好泛化和非线性处理能力,拟合降水量分布与环境变量之间关系,得到精细尺度降水量分布图,在省域尺度具有较好的预测效果。
2)相较于经典OK、IDW插值法,SVR存在明显优势,即拟合非线性关系进而改善降水量空间插值能力,并可应用于其他雨量变量的空间插值和预测研究中。
3)SVR模型的稳健性需考虑数据平衡性和参数率定,grid search方法可帮助对模型超参数进行快速寻优。此外,还发现一些站点数据量不足、模型偏差等问题,建议今后研究中加入更多敏感性变量如距离海陆位置远近、大气含水量等,进一步优化插值精度。
