基于地形断面参数辨识的泵站水动力模型研究

柯 仁,秦 锴

(1.深圳市水务规划设计院股份有限公司,广东 深圳 518001;2.中国建筑第四工程局有限公司,广州 510000)

0 引 言

在社会和经济发展以及保障社会健康等诸多层面上,水资源具有不可替代的重要地位[1]。我国作为农业大国,由于特殊的地理和气候条件,同时面临着水资源时空分布不均、供需矛盾突出、水质恶化和水资源利用率低的问题,使社会经济发展受到水资源的强烈制约。南水北调工程是解决华北地区严重缺水问题的重要战略,经过多年的探索、规划和研究,长江流域规划出东西中3条调水线路[2]。其中,河道被用作送水载体,泵站被用作主要控制结构,从低洼水源区开始,通过泵站的提水功能,将水输送至地势较高的接收区[3]。近年来,随着水资源调度理论和计算机技术的快速发展,研究人员试图对各种引水工程进行自动化和智能化调度,以保证工程的安全和稳定[4]。由于地形参数的不足以及水流撞击等诸多干扰因素,将会带来调水系统的计算难题[5]。因此,有必要研究泵站的输水特性,以实现准确的水力控制,并找到一种在地形数据缺失的情况下描述流量的方法,从而消除模拟建模对河流地形的依赖[6]。

鉴于此,本文提出一种基于数字高程模型(Digital Elevation Model,DEM)和敏感性分析方法,来优化现有水动力模型,以期优化调水工程决策问题。

1 面向地形数据缺失的泵站水动力计算模型优化

1.1 考虑水力损失和河道蓄量的一维水动力快速计算模型

一维流体动力学模型易于构建、计算快速且准确,可用于传感和计算水流状态。在输水过程中,水流的摩擦和冲击可能导致水力损失,泵站的调节会导致水道的蓄量变化[7]。此外,包括降雨、非监督流入和排水等干扰,可能会使水道中的水流难以控制。鉴于此,本此次研究将采用一维水动力模型,分析河道水力的运动规律[8]。图1为水力特性分析示意图。

图1 水力特性分析示意图

明渠一维流体运动的基本方程是Saint-Venant方程。为了获得明渠的流体动力学模型,必须添加边界条件,才能构建一个闭合形式的方程组[9]。设置边界约束时,一般从流量角度、水位角度或者两者关系角度出发。第3种边界条件因可能导致计算不稳定,而难以将水位关系应用于上游的外部边界[10]。因此,在边界条件上,上游和下游有5种流体流动模型。水力损失以及河道蓄量可以借助边界条件的组合实现计算。图2为河道水力损失计算示意图。

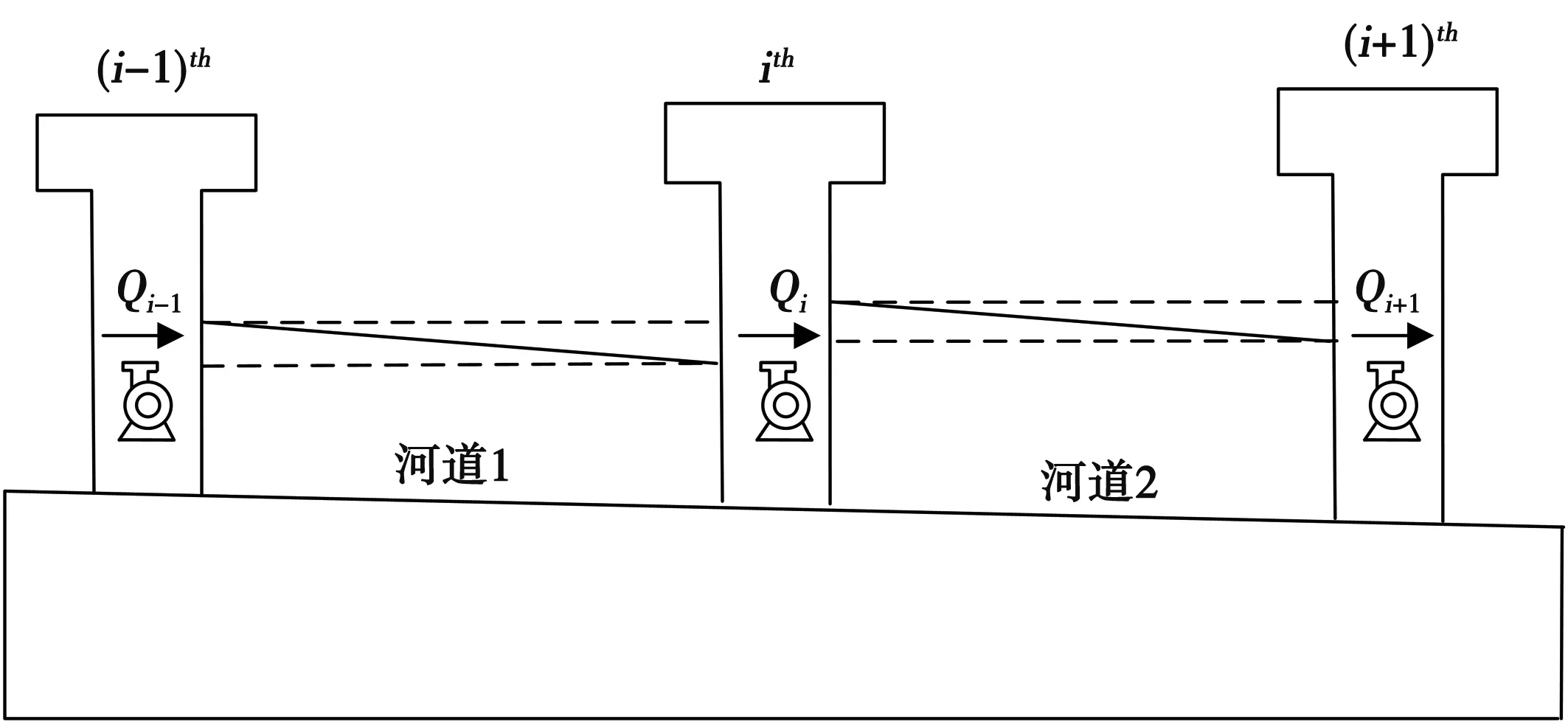
图2 河道水力损失计算示意图

河道水力损失的第一种方法是通过上游流量、下游水位作为边界条件,以实现对一维稳定水流进行建模,然后从下到上分级求解水面线,计算水流的水力损失。第二种是通过水流的上游水位和下游流量作为边界条件来模拟一维稳定水流,然后从上到下分级求解水面线,计算水流的水力损失。考虑到河道蓄量的计算便利性,研究采用一维恒定流量模型来计算河流上下游的流量[11-12]。

在供水渠的运行过程中,难监测、不可控的水量扰动会给河道蓄量计算带来计算偏差。为了准确求解水量,研究提出一种将水平衡与水力特性分析相结合的新方法来估计通道中的非监测湍流,公式如下:

(1)

1.2 基于DEM和LH-OAT的地形断面参数识别模型优化

水流横截面的几何轮廓对河道的流体动力学模拟至关重要。通常,测量容器用于测量河流横截面的几何形状,并通过插值处理该区域,以描述整个河道的地形。由于部分河道地形水文条件恶劣,水动力数值模拟模型难以建立。为了解决这个问题,研究使用观测数据驱动方法,建立一个未映射的河流水动力学模型[13]。在该模型中,利用水下DEM数据,对河道中的水下地形进行梯形综合处理,并基于LH-OAT全局灵敏度分析模型识别关键元素。通过粒子群算法在地形资料缺失情况下描述河流地形,从而实现更准确的水动力描述。图3为地形概化过程示意图。

图3 地形概化过程示意图

从图3可知,人工开挖明渠流道的横截面具有对称性和规律性。为了满足一般稳定性、最小河道、最小开挖量,河流断面的几何形状通常采用等腰梯形。但如果用等腰梯形来直接扩展横截面,则其对于断面真实模拟度将减弱。

DEM由一系列不同类型的数据空间分布组成,其中高度用于表示表面特征,垂直坐标系用于描述高度空间。利用开源DEM数据,可以获得水下地形的几何信息,且这些信息可以被推广。图4为LA-OAT方法流程图。

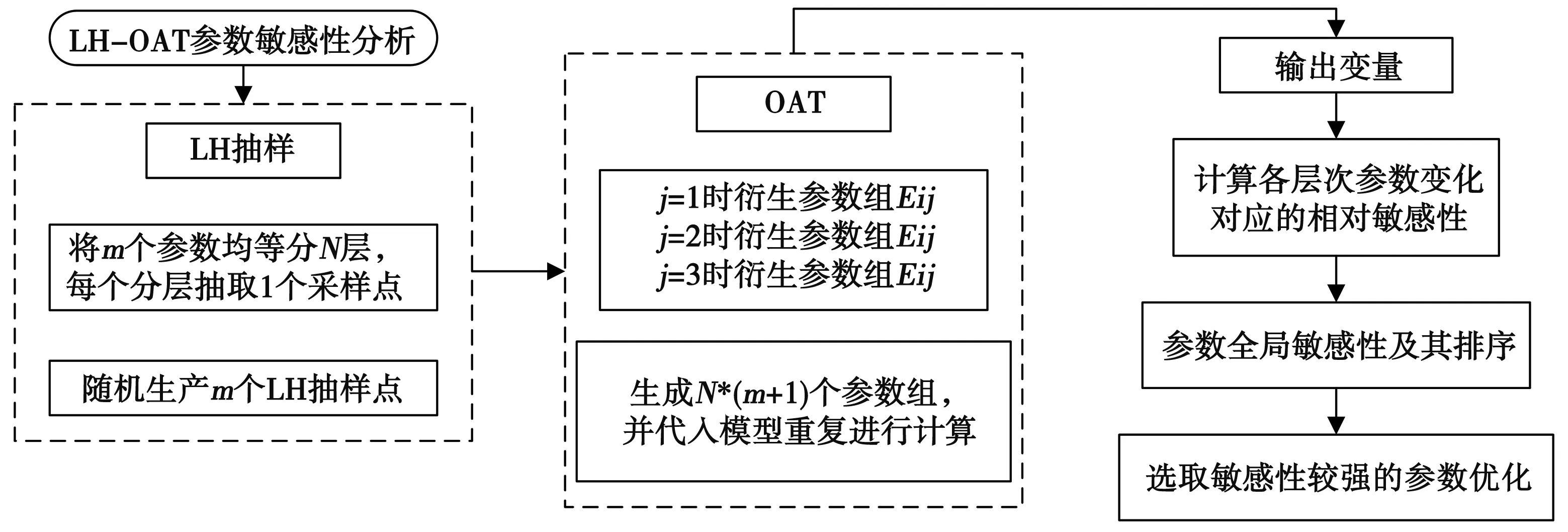
图4 LA-OAT方法流程图

LH-OAT(Latin hypercube-One factor at a time)算法基于Latin-Hypercube抽样法和OAT敏感性分析组成。根据LH的抽样概念,整个参数空间将进行堆叠,并随机选择每个级别。在将参数空间划分为n个级别的情况下,产生包括P参数的一组数量为n的LH采样参数。然后,根据OAT方法,小幅度修改LH采样参数,以计算目标函数的变化。流体动力学模拟中,存在多种输入元素。应用LH-OAT模型,对截面的深度和表面粗糙度进行分析,关键要素可以得到有效和正确的识别。本研究基于历史观测水位,借助粒子群优化算法,通过关键要素识别来确定决策变量。水位或流量计算值和实际值之间的偏差目标函数公式如下:

(2)

式中:zm、zo分别为模拟计算水位和实际水位,m;N为测量次数。

粒子群算法基于鸟类觅食行为启发而来,因此将解空间视为鸟的运动空间。每只在运动空间中飞行的鸟都被称为粒子,它会寻找最佳的全局位置进行求解。粒子速度和位置更新公式如下:

(3)

2 基于DEM和LH-OAT优化地形参数的水动力模型结果分析

为了验证研究所提基于DEM和LA-OAT算法优化的水动力模型有效性,选择南水北调工程中3个泵站作为实验对象,其装机台数分别为5、4、4,单机流量分别为30、20、10m3/s。仿真时,模型边界条件选为上游流量和下游水位,以进行恒定流水动力模拟,并计算水力损失。

从图5可知,在0～160h的观测时间内,起始时间的水力损失计算值49cm,水力损失实际值45cm,差值4cm,差值百分比约8.8%。当观测时间为75h时,水力损失计算值48cm,水力损失实际值56cm,两者差值8cm,差值百分比约14.2%。

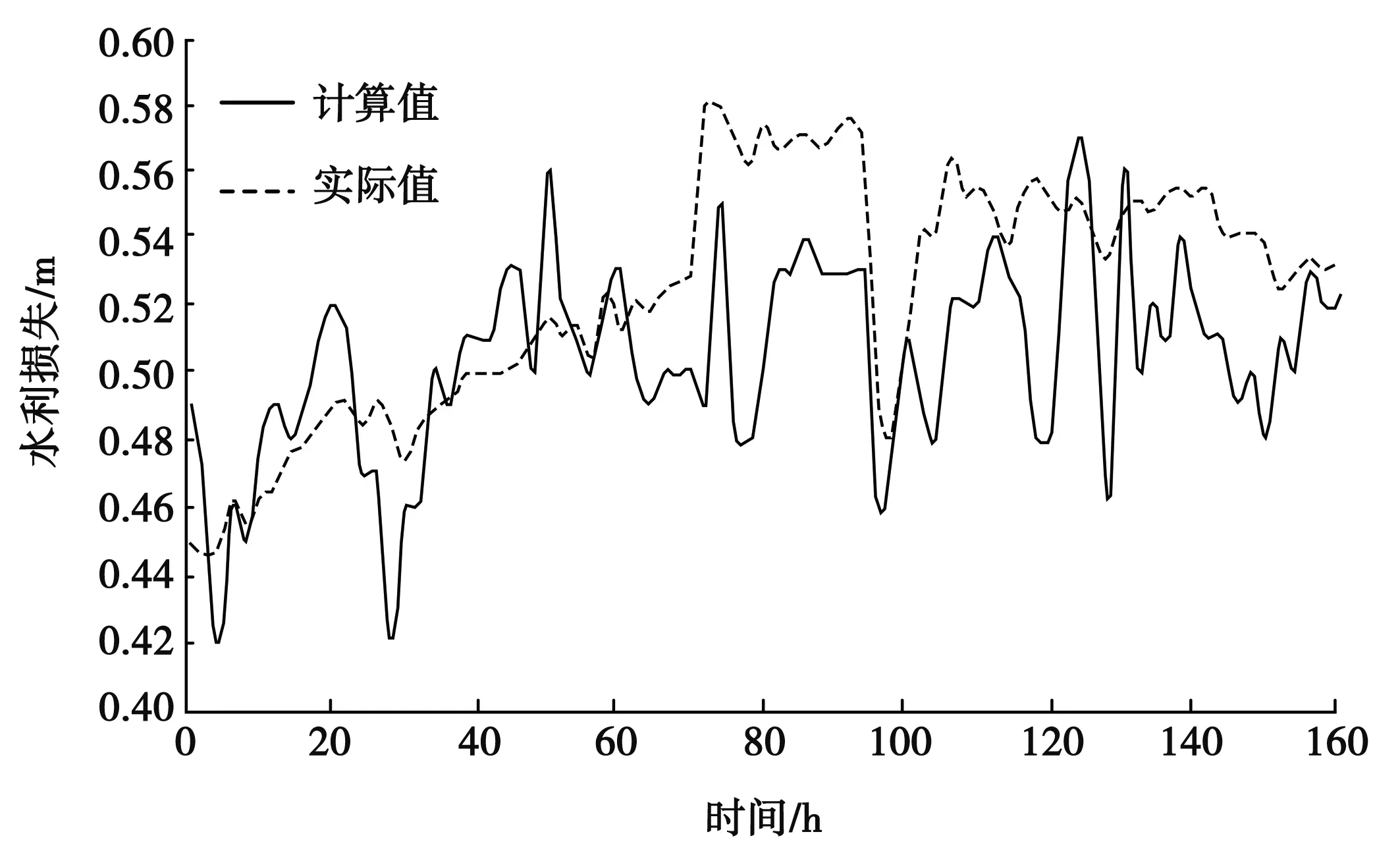
图5 水力损失值计算值和实际值对比曲线

整体而言,水力损失计算值在46～54cm之间波动,小时内波动范围不超过1.5cm,最小值和最大值分别为42和57cm。且在120h之后波动较为剧烈,波动频次和幅度明显增加。而水力损失实际值大多在48～56cm之间波动,小时内波动范围不超过1cm,最小值和最大值分别为45和58cm。

此外,研究所提水动力模型所得水力损失值计算值曲线与水力损失实际值曲线平均误差在3.4cm。经计算,其纳什效率为0.42。因此,模拟结果较为客观,表明该方法适用于进行水力损失的快速计算。

从图6可知,在率定期实验中,研究所提模型水位计算值在37.5～49.0cm之间波动,而水位观测值在40～50.5cm之间波动。两者波动区间差值不大,最小值和最大值分别相差2.5和1.5cm。此外,从曲线升降上看,两条曲线仅在时间为20、60以及110h变化趋势不一致,其余时间均具有相同走势。验证期实验中,模型水位计算值和观测值的最大差值出现在90h处,大小为5cm。两条曲线除了在时间为70h处的增减变化不同外,其余时间点处均保持相同变化趋势,表明研究所提模型水动力模拟结果较为精确。

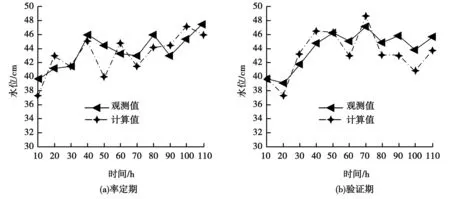
图6 模型率定期和验证期计算对比曲线

从表1可知,当迭代次数大于或等于40次时,横断面数量在取值为1～5之间时,其对应的平均误差均低于4cm,且从迭代次数为40开始,其平均误差稳定在3.8附近波动。当迭代次数为60,横断面概化数量在1～5之间变化时,其对应的模型平均误差距离3.8差值分别为+0.03、-0.11、+0.02、-0.02、+0.02。因此,横断面概化数量对计算结果和优化截面的效率几乎没有影响。但考虑工作量将随着推广的数量递增,建议减少横断面插值。

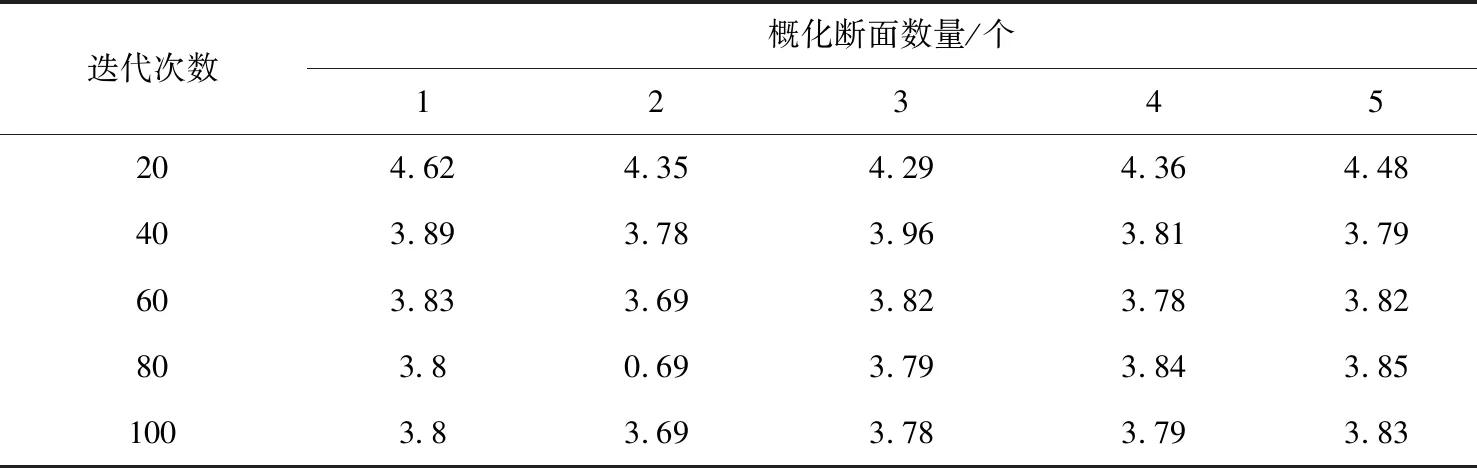
表1 横断面概化数目对模型平均误差的影响

3 结 论

为了优化泵站调水工程调度分析,本次研究将未勘探的地形断面河道作为研究对象,提出了一种基于DEM和敏感性分析优化的水动力模型。结果显示,率定期水位计算值和水位观测值差值不大,最值差值均低于3cm;验证期水位计算值曲线和观测值曲线几乎保持相同变化趋势。此外,断面概化数目对于模型优化结果影响不大,当迭代次数为40次之后,平均误差均低于4cm。表明研究所提模型水动力模拟结果较为精确,有助于输水河道水力的精准控制。