基于神经网络的零航速减摇鳍模型参考自适应控制设计

齐 雪, 石满红, 董姗姗, 潘 花

(安徽科技学院 信息与网络工程学院,安徽 凤阳 233100)

无论是平静水域还是复杂海域,船舶都会产生摇荡运动。并且环境所带来的外部干扰是无法完全避免的,这些干扰对于船舶的横摇运动影响最大,所形成的危险性也最大,所以,对于船舶的横摇控制是必须要考虑的问题。目前, 减摇鳍是技术较成熟且实用性最大的船舶减横摇装置,具有主动减摇的工作机理,高速状态下减摇效果达90%以上。受船舶航行速度的影响,减摇鳍的控制效果也不尽相同。当船速较高时,减摇效果能达到最佳状态;但是,当船速较低或者为零时,减摇效率就大大降低了。此外,减摇水舱也是一种常用的船舶减横摇装置,减摇水舱的优势在于其放宽了对船舶航速的限制,可以弥补减摇鳍的不足;缺点是体积较大,减摇效果受制于谐摇频率的大小,即船舶在谐摇频率附近做摆动时,减摇水舱能够实现最好的减摇效果,即显性减摇效果好,但是当船舶以远离谐摇频率做摆动时,减摇水舱工作能力下降,甚至会出现增摇的现象[1-3]。鉴于对减摇鳍和减摇水仓优缺点的对比,为了使减摇装置适合于船舶零航速的特殊情况,学者们提出了零航速减摇鳍的概念。

船舶零航速减摇概念的提出是基于其广泛的应用背景而言的。中国一直在积极推进海洋领域的探索和开发工作,近年来随着海洋工程项目的增多,需要船舶在零航速下工作也变得越来越频繁,为了保证船舶在风浪条件下仍然有平稳安全的工作环境,就迫切需要对船舶进行减摇。一般情况下,长浪的周期是7～14 s,而大马达游艇的横摇周期是6～11 s。由于海浪的周期跟停泊状态下船舶的横摇周期相近,那么即使在浪高很小的情况下,船舶也会剧烈横摇[4-6]。

手稿中，除了画，还有一部分是文字手稿。内容多为李铁夫自己的诗词、楹联创作，少数是抄录他人作品。部分手稿因为几幅合裱在一起，账本登记中只给了一个藏品号，所以有一个藏品号包含了数件作品的情况（如藏品“诗稿”为三个藏品号，实际共六幅作品）。

20世纪90年代,许多科研机构开始对零航速状态下船舶减摇问题进行了系统性、探索性研究。从经济实用性角度考虑,可以设计一套减摇鳍系统在不同的航速间切换工作状态。当船舶以中高航速行驶时,减摇鳍切换到传统工作模式以实现减摇目标;当船舶以低速行驶或系泊状态工作时,减摇鳍切换到振动模式来产生升力,进而完成减摇任务。文献[7]提出基于Weis-fogh机构和单翼拍动工作方式的两种设计方案,试验数据和实践应用进一步验证了该设计方案的优越性。文献[8-9]对减摇鳍在零航速下升力产生机理进行了深入研究,形成一系列研究成果。

由文献[10-12]可知,零航速减摇鳍升力模型具有非线性特征,其相关变量为鳍角度、鳍角速度和鳍角加速度。模型中参数具有不确定性,这给实际操作带来了很大困难。文献[7]和[13]基于Weis-fogh减摇方案设计了经典PID控制器,该控制方法将船舶横摇模型在期望工作点附近进行线性化处理,针对此线性化系统进行减摇控制。这种严格的线性化约束会导致远离期望工作点处控制失效的后果。因此需要进一步考虑模型不确定性和非线性的实际状况。文献[14]通过对波浪扰动、船舶横摇运动、鳍运动和鳍诱导水动力的相位匹配分析,得出了基于扰动和补偿的控制策略。文献[15]采用相位匹配控制策略,同时对减摇鳍常规减摇和零航速减摇进行了分析和研究,该控制研究是在线性横摇理论的基础上展开的,没有考虑模型的不确定性和参数的时变性。文献[16]设计了混沌遗传算法的自适应控制器来实现大型船舶非线性减摇的效果。文献[17]采用分数阶自适应滑模方法进行船舶非线性减摇控制。文献[18]基于船舶横摇模型非线性、非稳态的特点,加入积分过程,形成模糊积分控制。

零航速减摇鳍系统原理如图1所示。

为了解决船舶横摇模型参数的不确定性问题,本研究设计自适应控制器,该控制器使船舶横摇角跟踪指定的参考模型输出信息。参考模型为一个期望的理想系统。参考模型的输入量与真实系统的输入量相同,参考模型的输出量为期望结果。系统以参考模型输出与真实被控对象输出的差异大小作为调整控制器参数的依据,从而使得真实系统的闭环控制性能与参考模型的性能保持一致,这些性能包括系统时域特性和频域特性[19-20]。零航速减摇鳍的升力力矩为非线性不确定系统,本研究采用径向基函数神经网络[21-22]在线逼近重构误差。本研究仅以减摇鳍鳍角速度作为测量元件,则实际控制量为鳍角速度,通过设计鳍角速度的大小形成合适的控制力矩作用在船舶横摇模型上,以达到理想的减横摇效果。

1 横摇模型介绍及分析

船舶横摇模型被广泛应用于工程实践中,其中,用于刻画小角度下的横摇线性方程为Conolly模型,其线性二阶微分方程模型可以表述如下[11]:

(1)

其中,Ix和ΔIx分别为相对于通过船舶重心纵轴的惯量和附加惯量,2Nu为每单位横摇角速度的船舶阻尼力矩,D为船舶排水量,h为横稳心高,φ为横摇角,Kw为海浪干扰力矩,K为减摇鳍产生的对抗海浪干扰的控制力矩。上述参数并不是恒定不变的常数,随着船舶装载情况的变化以及海况的复杂变化,横摇模型参数也会随之改变,即参数具有时变性;并且参数变化受多变量影响,具有非线性特征。

紫外分光光度计（UV2400型，上海舜宇恒平科学仪器有限公司）；高速逆流色谱（TBE－300B型，上海同田生化有限公司）；微量分析天平（TP－214型，美国丹佛仪器有限公司）；超声清洗机（KQ32002型，昆山市超声仪器有限公司）；高压灭菌锅（MLS－3780型，日本三洋公司）；恒温培养箱（DHP－9162型，上海齐欣科学仪器公司）；超净工作台（SW－CJ－1F型，苏州安泰空气技术有限公司）。

令a2=Ix+ΔIx,a1=2Nu,a0=Dh。

1.6 他汀类药物停药指征 当出现以下指征时，考虑停药或更换剂量：（1）年龄≥80岁，AST、ALT超过正常上限2倍。（2）年龄＜80岁，AST、ALT超过正常上限3倍。（3）CK超过正常上限5倍且（或）伴有肌痛、乏力、酸困等他汀类药物相关不良反应。（4）表皮生长因子受体（eGFR）下降≥50%。

则a2,a1和a0会随着海情或船舶装载情况的变化而变化。

2 零航速减摇鳍的升力模型

龙庆峡位于北京市延庆县城东北10公里的古城村西北的古城河口，距北京城区85公里。龙庆峡古称"古城九曲"，被人们誉为北京的"小漓江"，是北京十六景之一。其水源于海坨山东麓，经玉渡山汇入古城水库。

图1 零航速减摇鳍系统工作简图Fig.1 Schematic diagram of zero speed fin stabilizer system

零航速减摇鳍较常规减摇鳍而言增加了运动模式切换系统,即在船舶中高速运动过程中,控制系统通过改变减摇鳍的攻角来调节升力[7],从而实现减摇目标;在船舶低速或系泊状态下,控制系统驱动鳍翼绕鳍轴在水平位置附近做振动,由于振动频率的不同而产生不同大小的升力来抵抗外部干扰。本研究只考虑船舶零航速下的减摇问题,减摇鳍运动方式如图2所示。

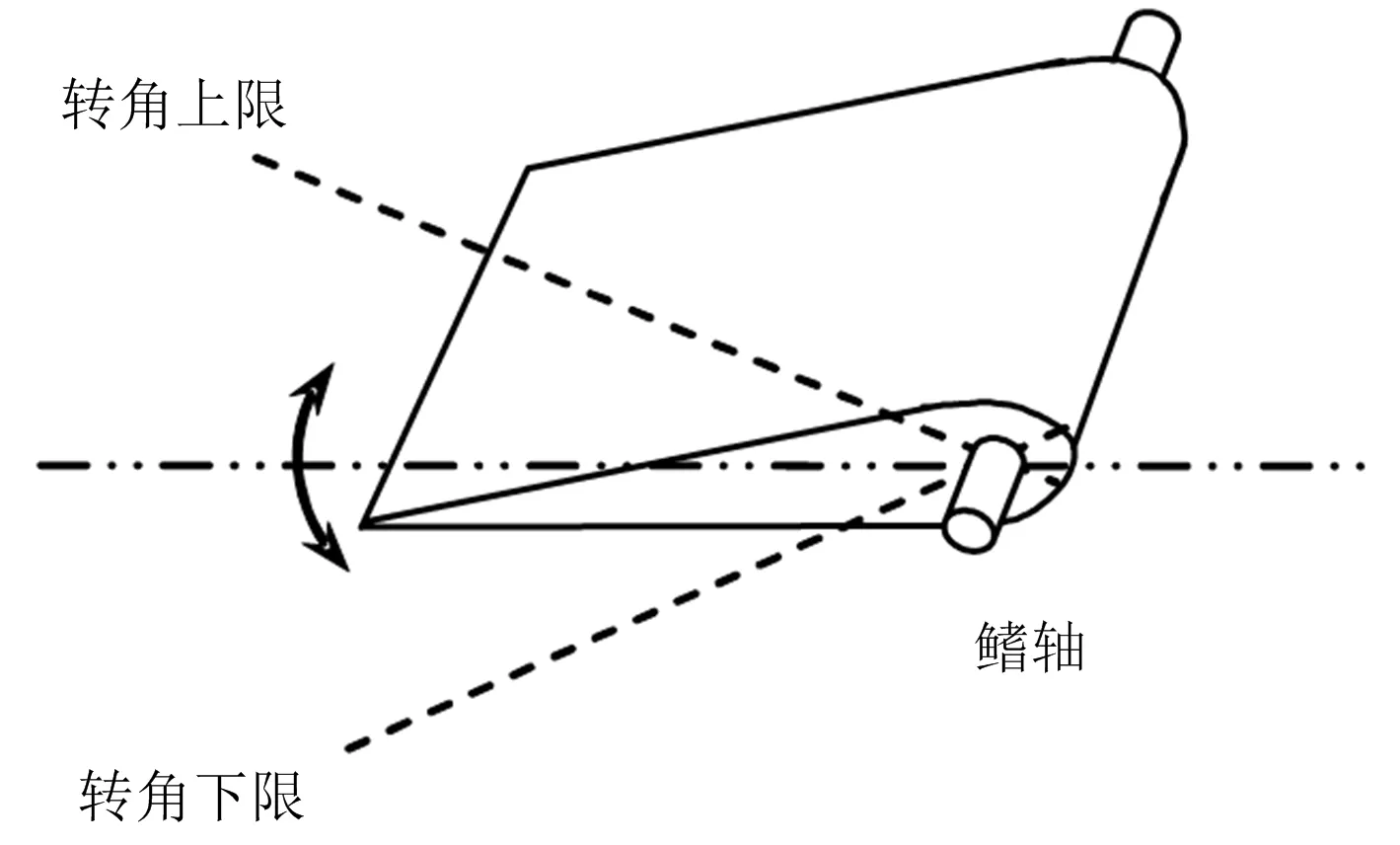
图2 零航速减摇鳍工作方式Fig.2 Working mode of fin stabilizer at zero speed

对于零航速减摇鳍来说,升力力矩K的表达式如下:

(2)

其中,k1、k2为常数,ω为减摇鳍绕鳍轴的旋转角速度,α为减摇鳍与水平位置的夹角。控制力矩随着鳍角及其运动方式而发生变化,需要控制这些影响力矩的变量大小,从而达到有效的减摇效果。由升力力矩模型式(2)可知,零航速减摇鳍升力模型是一个非线性结构,其相关变量为鳍角度、鳍角速度和鳍角加速度。由于

α=ωt

(3)

(4)

3 控制器设计及稳定性分析

则

图3 控制器结构图Fig.3 Controller structure diagram

设参考模型为:

资源依赖学派认为，面对环境的束缚，组织也会主动对环境进行管理和控制，组织采取各种策略以减少其对外部环境的依赖以及来自外部环境的制约，这充分体现了组织在与环境关系中的积极主动性⑧。社工组织在遭遇互动困境的时候，也不是被动地接受约束。社工组织也会采取各种互动策略，从而获得更多资源的支持，进而获得自主发展的机会。

(5)

其中,r(t)是有界参考信号。

对于式(2),设

(6)

爱情，就像“三国”，合久必分，分久必合；爱情，也像“西游”，九九八十一难，方才取得真经；爱情，更像“红楼”，总有一些人把它奉为圭臬，耗费毕生研究它；爱情，最像的还是“水浒”，管你有多轰轰烈烈，最终都得被生活招安。

设虚拟控制器:

(7)

(8)

式(1)可以重记为:

(9)

定义信号z(t)为:

(10)

其中,e=φ-φm为跟踪误差,β1、β0是使得p2+β1p+β0成为稳定(胡尔维茨)多项式的正常数。在式(9)两边加上(-a2z(t))并整理,将被控对象动态改写为:

(11)

令

(12)

选择虚拟控制器:

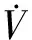
(13)

其中,Φ(ω)∈RL×1为径向基函数,通常选为高斯函数,即

4.BEPS第15项行动计划成果的重要贡献。中国国家税务总局积极参与“引入多边工具”的制度建设，2015年11月，OECD牵头成立了《实施税收协定相关措施以防止税基侵蚀和利润转移(BEPS)的多边公约》(以下简称《协定公约》)特别工作组，共同研究起草《协定公约》文本。其中，中国当选为该工作组第一副主席国，积极参与组织《协定公约》的研究制定工作，并与其他100多个国家进行了为期一年的集体谈判与磋商，为《协定公约》的制定