次线性期望下负相依随机序列加权和的完全收敛性
2023-09-15陆卫国郭明乐
陆卫国, 郭明乐
(1.铜陵学院 数学与计算机学院,安徽 铜陵 244000;2.安徽师范大学 数学与统计学院,安徽 芜湖 241003)
随着科技和经济的跨越式发展,现实世界中各种问题的不确定性变得越来越大,对可能产生的风险进行预测和控制变得十分困难。Peng等[1-2]受到金融领域中的风险评估及波动的不确定性启发,给出了次线性期望下独立同分布的随机变量的概念[1-4],定义了G-期望、G-布朗运动,建立了理论框架。由于次线性期望的应用广泛性,迅速引起国内外许多学者的关注,形成一个新的研究热点。在次线性期望框架下,Zhang[5]获得了部分和最大值不等式和Kolomogov强大数律,Chen[6]、Hu[7]、Wu等[8]建立了强大数定律,Zhang[9]研究Donsker's不变原理和Chung's重对数律,冯凤香[10]对强大数定律、完全收敛性、完全矩收敛性以及几何权级数的正自则重对数律进行了研究。因为次线性期望和容度的不可加性,目前次线性期望理论仍处于发展中,有很多问题亟需解决,以期更好地为社会、统计、金融和科技服务。
从Borel-Cantelli引理可以得到完全收敛蕴含几乎处处收敛。Hsu等[11]证明当方差有限,独立同分布随机变量序列的样本均值完全收敛于总体均值。而袁千顺[12]证明在{Xn,n≥1}是独立的情形下,其逆命题也成立。Hsu等以及袁千顺的研究结果是概率论中的一个基本定理。时至今日,已有许多学者在不同方向领域中推广并完善了完全收敛性的结果,获得了丰富的理论成果,其中一项重要的推广是胡泽春等[13]给出了独立同分布随机变量序列的完全收敛性的等价条件。Chen等[14]讨论了负相协(NA)随机变量序列的完全收敛性,郭明乐等[15]将其推广到负相依(ND)随机变量序列,克服了ND随机变量序列的Rosenhtal型不等式中的系数不为常数的难点。
本研究将上述结果推广到次线性期望下负相依随机变量序列情形,采用Peng的次线性期望理论框架。设(Ω.J)为可测空间,H是由定义在(Ω.J)上的实函数构成的线性空间,使得对任意的φ∈Cl,Lip(n)若X1,X2,…,Xn∈H,则φ(X1,X2,…,Xn)∈H,空间H称为随机变量的集合,这里Cl,Lip(n)表示满足如下条件的局部Lipschitz函数φ组成的线性空间,|φ(x)-φ(y)|≤C(1+|x|m+|y|m)|x-y|,∀x,y∈n,此处常数C>0,m∈仅依赖于φ。
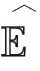
(II)(常数不变性):若c∈,则

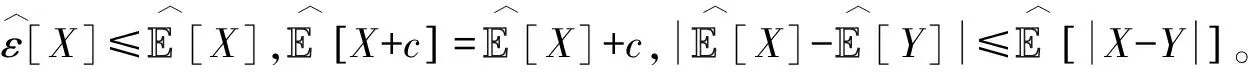
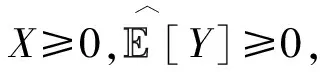

接下来,介绍对应次线性期望的容度概念。令g⊂J,如果函数V:g→[0,1]满足V()=0,(Ω)=1和V(A)≤V(B),∀A⊂B,A,B∈g,则称V为容度,如果容度V 还满足:V(A∪B)A≤V(A)+V(B),∀A,B∈g,则称容度V是次可加的。
(AC),∀A∈J,
其中,AC为集合A的补集。
通过次线性期望的性质,可以看出若f≤I(A)≤g,f,g∈H,则
对任意的X∈H,有
为了得到Borel-Cantelli引理,还需假定容度V具有次可列可加性。
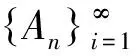
Choquet积分/期望定义如下:C
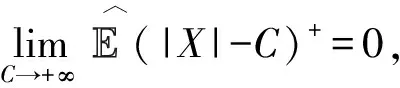
1 次线性期望的性质
为了叙述本研究的主要结果,先叙述一些记号和引理。约定:本研究中的C表示正常数,在不同的位置可表示不同的值;logx表示ln(max(e,x));an≪bn表示存在常数C>0,使得an≤Cbn。本研究主要结论中要用到的局部Lipschitz函数h,定义如下:设0
显然
I(|x|≤a)≤h(x)≤I(|x|≤1),I(|x|>1)≤1-h(x)≤I(|x|>a)
(1)

通过对学生课业学习质量等教育大数据资源的多尺度分析、数据集成、关联模式分析和数据深度挖掘分析,各高校能够透析学生的质量和学习行为之间的联系,对于学生作出具有个性化、全面化的综合分析报告、舆情分析、情感变化和能力分析,有助于学生的个性化学习方案制定与全方位能力评估。
(Sn≥x)≤

(Sn≥x)≤
(2)
(|Sn|≥x)≤2
(3)

(ii)当p>2时,存在仅依赖于p的正常数C ,使得
2 主要结果
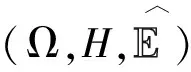

则:
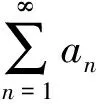
(4)
证明利用容度的单调性及条件(iii),为证式(4),仅需证明:
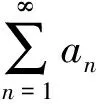
(5)
(|Xni|>aδ)+
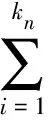
(6)
利用条件(i),只需证明:
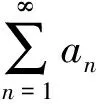
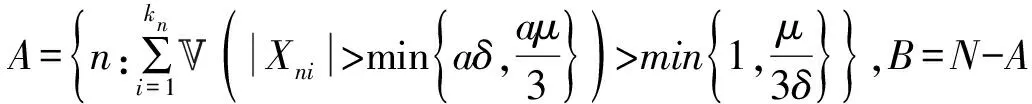
对n∈A,利用条件(i)可得:
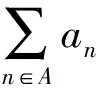

(7)
因此,为了完成定理3.1的证明,仅需证明:

(8)
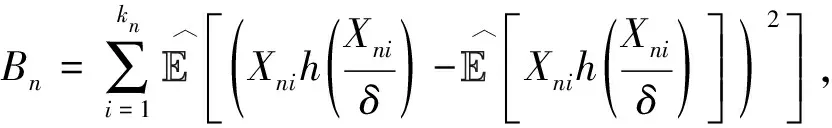

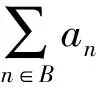
(9)
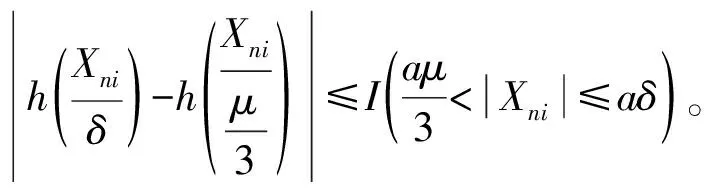
从而,当n∈B时,
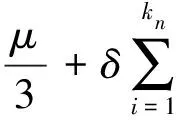
(10)
若μ/3≥δ,则:
(11)
从而由式(6)和(7),再利用条件(i),得:

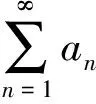
(12)
(13)
从而由式(8)、(9)可知式(4)成立。
注3.1从定理3.1的3个条件可以看出,研究次线性期望下的完全收敛性,往往需要构造局部Lipschitz连续函数h来替代示性函数,达到解决问题目的。同时,要注意的是,∑Xni是不能随便加绝对值的,这主要还是次线性期望不具有可加性导致的。
3 结论
利用Hölder's不等式,给出更易验证的完全收敛性3个条件,得到如下的结论。