基于仿冰壶火炬传递机器人的全向轮运动设计研究

王福利，陆洋

（1.中国科学院 沈阳自动化研究所，沈阳 110016；2.中国科学院 机器人与智能制造创新研究院，沈阳 110169）

0 引言

移动机器人是机器人领域的移动机构的一个重要组成部分，被广泛研究。按照移动方式，移动机器人被分为轮式、履带式、腿式、爬行式、跳跃式及复合式。而轮式移动机器人具有结构简单、运动建模容易、成本低、对场地要求低、运动灵活、稳定性和可靠性高等优点，被广泛应用。

根据移动特性，移动机器人分为全向移动机器人和非全向移动机器人[1]。当移动机器人同时具有前后、左右、旋转3个自由度时，则被称为全向移动机器人。不能同时具有3个自由度或者少于3个自由度的移动机器人则被称为非全向移动机器人。全向移动机器人克服了普通移动机器不能在3个自由度之间随意切换而带来的非完整性约束，能够在平面实现横移、斜移、旋转甚至更复杂的运动，实现全方位运动[2-3]。

全向轮是一种具有3个自由度的特殊轮子，一般由轮毂和从动轮组成，通过多个全向轮的组合，可以使机器人实现全向移动。这种由全向轮组成的全向移动机器人具有较好的机动性、灵活性等特点，逐渐成为全向移动机器人移动机构的主流。

全向移动平台作为全向移动机器人的运动执行部分，有着较为完整的体系和扩展性。它能够根据不同的应用场景搭载不同的移动轮组和不同的结构布局，实现不同的功能要求。

本文所设计的仿冰壶火炬传递机器人，由于实际传递场景运动曲线特性的特殊性（像冰壶一样，旋转的同时完成前进动作），如图1所示，对机器人的全向移动平台运动性能要求较高，对系统的加速度、速度、角速度等运动性能的物理量不断调整，使得机器人的运动性能始终为最优性能。

图1 机器人运行场景

1 全向移动平台设计与研究

1.1 全向轮的选择

全向轮作为全移动平台的运动执行机构的重要组成部分，其选择十分重要。全向轮是一种特殊的轮系，其特点是沿主轮毂圆周排布着与轮子成一定角度且可绕自身轴线进行旋转的从动辊子。根据从动轮组与主动轮毂平面角度不同，分为麦克纳姆轮和OMIN全向轮。麦克纳姆轮的从动辊轮相对于车轮平面成45°角，相对于穿过滚轮中心的平行于车轮旋转轴的直线成45°角。而OMIN全向轮则是在主动轮毂外轮廓上均匀分布着沿垂直轴分布的从动辊轮，从动辊轮的轴与轮毂轴正交[4]，如图2所示。

图2 全向轮示意图

麦克纳姆轮的优点为：外形美观，全向移动性能好，承重能力强，与地面摩擦力大、不易打滑。缺点为：加工难（金属材质较多）、造价高、速度较慢、寿命比传统胶轮短，每个轮子需要电动机单独驱动。OMIN全向轮的优点为：结构简单、易加工、成本低，原地打转时横向摩擦力小。缺点为：无法横向前进，承重能力较弱。两者还有一个共同的缺点：运动过程中都会横向卸力。为了保证运动的平稳性，当前一个辊子与地面即将分离时，后一个辊子必须与地面接触。因此在使用过程中，都选用双排轮结构的全向轮。

1.2 全向轮运动特性分析

1.2.1 单个全向轮运动特性分析

对于全方位机器人的运动机构，移动平台通常会通过多个全向轮组合来合成所需要的运动轨迹。不同数量、不同种类的全向轮组合成的运动轨迹是不同的，所以先对单个全向轮进行运动模型分析。

图3 O-XY坐标系全向轮位置关系

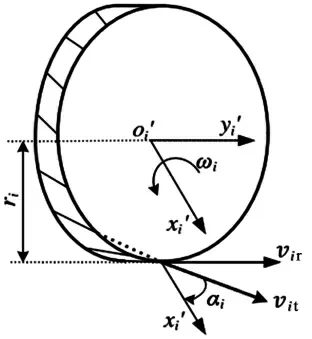
图4 全向轮坐标系参数位置关系

（xiyiθi）为全向轮本体坐标系到参考坐标系O-XY的位姿；ri为全向轮轮毂半径，vir为全向轮i沿着轮切线方向与地面的线速度矢量，以图3箭头方向为正；vit为辊子转动时沿着辊子转动切线方向的线速度矢量，以图3箭头方向为正；ωi为全向轮毂的转动角速度；θi为该全向轮的安装角，在O-XY坐标系下绕Z轴逆时针方向为正；looi′为全向轮中心oi′在参考坐标系O-XY下的位置矢量，坐标为（xiyi）；Ω为全向轮中心oi′在参考坐标系O-XY下绕Z轴的转动角速度，绕Z轴逆时针为正。

定义（vxvyΩ）T为参考坐标系O-XY整体运动的广义速度；（vixvix）T为全向轮中心oi′在坐标系O-XY上的速度矢量；（virvit）T为全向轮坐标系oi′-xi′yi′下的广义速度，其中vir与ωi满足如下关系：vir=ri·ωi。

1.2.2 单个全向轮运动方程分析

由图3可以看出，对于任意角度αi的全向轮，当给定广义速度（vxvyΩ）T时，通过运动合成，可以得出oi′点在O-XY坐标系下的速度分量（virvit）T，其矢量表达式为

根据式（1），将矢量分解为沿O-XY坐标系下的两个坐标轴：

将式（2）整理成矩阵形式：

令R1为式（3）从（vxvyΩ）T到（vixviy）T转换关系的矩阵，可得

定义R2为式（5）从（vixviy）T到（vix′ viy′）T转换关系的矩阵，可得

定义R3为式（7）从（virvit）T到（vix′ viy′）T转换关系的矩阵，可得

式（3）、式（5）、式（7）联合可得（virvit）T与（vxvyΩ）T的关系方程：

式（9）反映了参考系整体的（vxvyΩ）T速度与任意夹角辊子的转速、切向速度的关系。由det（R2）≠0、det（R3）≠0可得

已知

由式（10）和式（11）整理可得

式中：lx=-looi·sinωiθi、ly=looi·cos θi分别为全向轮到参考坐标系中心X轴和Y轴上的距离。

定义R为式（12）从（vxvyΩ）T到（ωivit）T转换关系的矩阵，因此

1.2.3 全向轮轮组布局分析

对于全向轮轮组，布局方式是轮的数目、布局的形状和间距的设计，从根本上讲，布局的方式取决于两种运动模型所组成的轮系雅克比矩阵的奇异性，以及对αi、βi、lx、ly参数数值的选取。当已知多轮系本体上的广义速度（vxvyΩ）T，为了能够获得每个轮所需的转速（｛ωi|ωi，i=1、2、3、4…｝），需要分析并得到多轮系运动学方程。

由式（13）可得出ωi与广义速度（vxvyΩ）T的关系为

由式（15）看出，系数矩阵R的列数为3，未知数个数也为4个（αi、βi、lx、ly），故对于全向轮组来说，ωi的个数至少为4。

对于已知αi角度的全向轮，以OMIN全向轮为例，由式（14）可得

由式（16）看出，系数矩阵R的列数为3，未知数个数也为3个（βi、lx、ly），故对于OMNI全向轮来说，ωi的个数至少为3。同理对于45°麦克纳姆轮也一样，ωi的个数至少为3。

1.3 常用全向轮轮系布局分析

对于全向轮组布局结构，国内外学者们进行了大量研究，这里只针对常用的三OMIN全向轮和四麦克纳姆轮，以及本机器人采用的四OMIN全向轮进行布局分析[6-7]。

1.3.1 三OMIN全向轮布局分析

建立三OMIN全向轮参考坐标系布局，如图5所示。

图5 三OMIN 全向轮坐标系布局

由式（16）得出三轮轮组的运动学方程为

而在最常用的三OMIN全向轮组中，β1=90°，β2=210°，β3=330°，两两夹角为120°，θi=βi，且loo1′=loo2′=loo3′=L，各个轮子半径均为r，如图6所示。

图6 三OMIN 全向轮正三角布局

简化后的逆雅可比矩阵为

1.3.2 四OMIN全向轮布局分析

建立三OMIN全向轮参考坐标系布局，如图7所示.

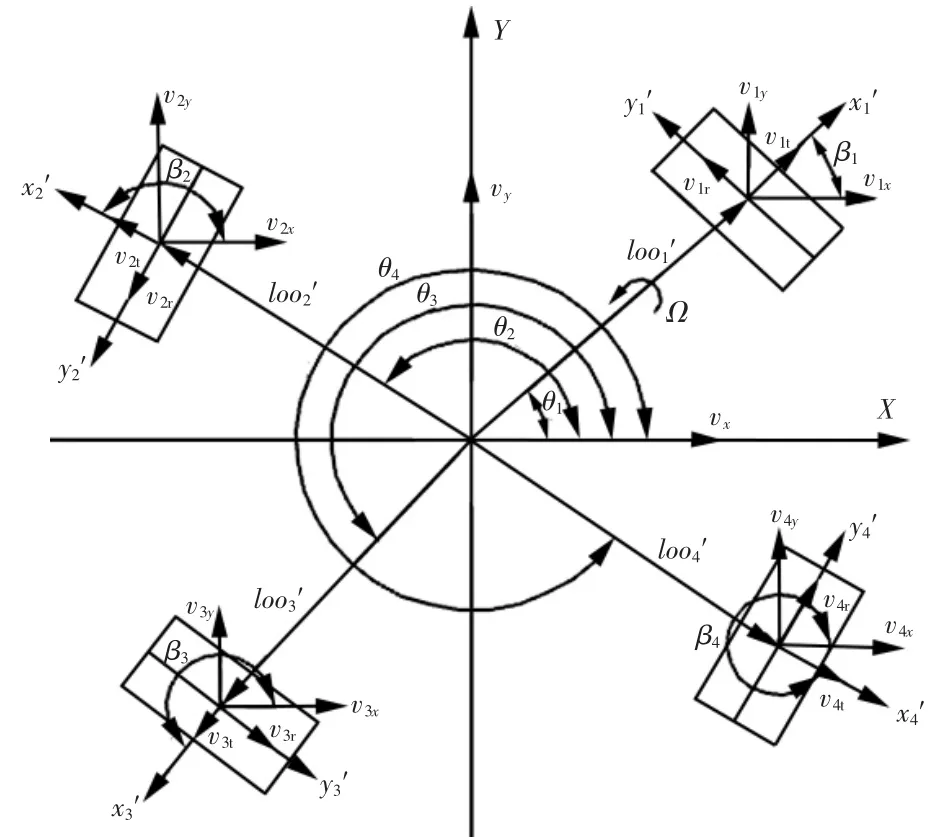
图7 四OMIN 全向轮坐标系布局

由式（16）得出四轮轮组的运动学方程为

常用布局中OMIN全向轮相对于坐标O-XY相互对称。根据lx与ly是否相等，可分为方型四角布局、长方形四角布局。对于方形四角布局，β1=45°，β2=135°，β3=225°，β4=315°，两两夹角为90°。θi=βi，且loo1′=loo2′=loo3′=loo4′=L，各个轮子半径均为r。如图8所示，对应的逆雅可比矩阵为

图8 四OMIN 全向轮方形四角布局

1.3.3 四麦克纳姆轮布局分析

由式（15）得出四麦克纳姆轮轮组的运动学方程为

图9 四麦克纳姆轮的两种布局

对于X型布局，4 个 轮 子 转动时，沿着Z轴转动的力臂短，力矩比O型小，通常不使用此方案。由O型布局 图 可 知，4 个麦克纳姆轮半径一致，即r1=r2=r3=r4=r，并且轮轴彼此平行，轮子安装方向垂直矩形边，即β1=β2=β3=β4=0，根据O型布局中的旋向，规定4个麦克纳姆轮αi的角度分别为α1=45°，α2=-135°，α3=-135°，α4=45°，且lx1=lx2=lx3=lx4=lx，ly1=ly2=ly3=ly4=ly。简化后JM4为

1.4 全向轮组的选用

上面分析的3种组合方式，都可以实现全向移动的功能，但是从布局方式上就可以看出很大的差距。

三轮组布局是理论上最简单的布局方法，具有控制方便、成本低的特点。但是少一个轮子就少了一个驱动电动机，相应的驱动力较小，而且三轮组结构容易造成一个轮子离地，从而导致整体稳定性变差。与之相比，四轮组结构多一个轮子，每个轮子所受的负载也减小。从布局上看，四轮组布局结构对称，在某一方向的直线移动更加精准，无需传感器辅助。

单个OMIN全向轮与麦克纳姆轮各有优缺点。但是从轮组布局上，四OMIN全向轮布局的旋转效率更高，而四麦克纳姆轮组布局的运动效率更高。全向轮运动的平台一般要求地面平整，而且有较大的摩擦力。四麦克纳姆轮甚至可以在相对复杂的场地上运动[8]。

虽然四麦克纳姆轮轮组布局比四OMIN全向轮更有优势，但是本文涉及的仿冰壶火炬传递机器人的外形为圆形的冰壶形状，且对于机器人的旋转特性要求要更高一些。另外，冰壶机器人的运动环境主要为冰上运动，为了防止全向轮运动时打滑，需要优先选用摩擦力较大的全向轮。故最终选用四OMIN全向轮布局为全向最终移动平台，如图10所示。

图10 仿冰壶机器人全向轮布局

2 全向轮运动电动机控制设计与研究

电动机控制系统设计是为了实现机器人陆地全方位移动作业，它采用以太网与CAN混合组网的设计方式将各个单元部件联系在一起。当有大数据传输时，各单元之间通信采用以太网通信方式，控制命令与状态数据反馈则主要采用CAN总线来完成。具体设计的结构如图11所示。

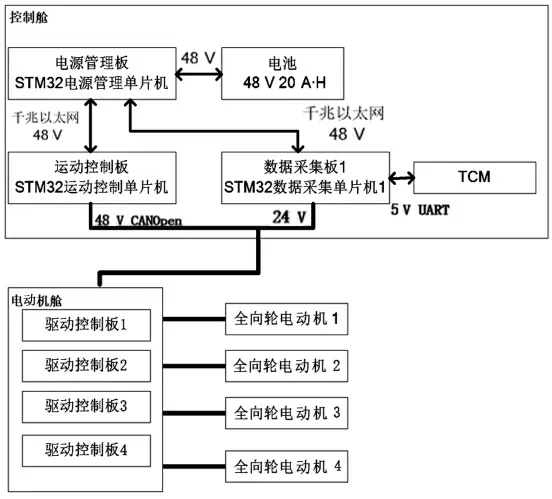
图11 控制系统结构图

电源管理单片机管理电池电量并监测能耗，同时为运动控制单片机与数据采集单片机供电并通信。运动控制单片机分别控制电动机舱内的4个驱动控制板，驱动板分别控制全向轮电动机运动，通过速度分解获得每个车轮轮毂的转速分量之后，采用矢量控制原理进行全向轮电动机控制，数据采集单片机采集各电动机驱动数据和TCM电子罗盘的数据反馈，通过带有实时操作系统的DSP实现同步和运动控制，达到期望的运动状态，如图12所示。

图12 火炬传递机器人设定轨迹示意图

依照设定要求，对机器建立了运动学模型观测，通过试验测得机器人角速度、艏向角、速度数据，如图13～图15所示。

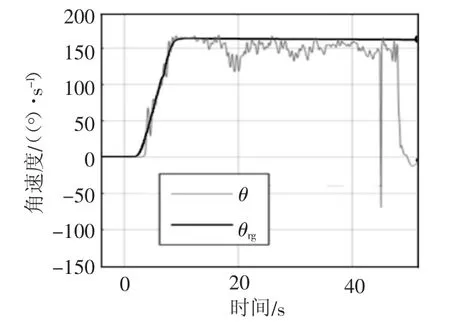
图13 角速度曲线图

图13中灰色线条θ为角速度传感器陀螺仪测量到的机器人的实时角速度，黑色线条θrg为动力力学模型根据全向轮动力输出预测的机器人的角速度。可以看出预测角速度都与传感器测量值差别不大，仅有一些短暂的误差及一些瞬时的扰动。由图14可以看出，在机器人运动的过程中，机器人艏向的期望角度与实际角度基本一致，旋转性能良好，控制准确稳定。图15中灰色线条v为机器人前进速度，黑色线条vrg为机器人理论前进速度，不难看出机器人均速与理论速度基本吻合，但波动较大、稳定性差，电动机控制效果不够理想，但不影响机器人达到预期效果。

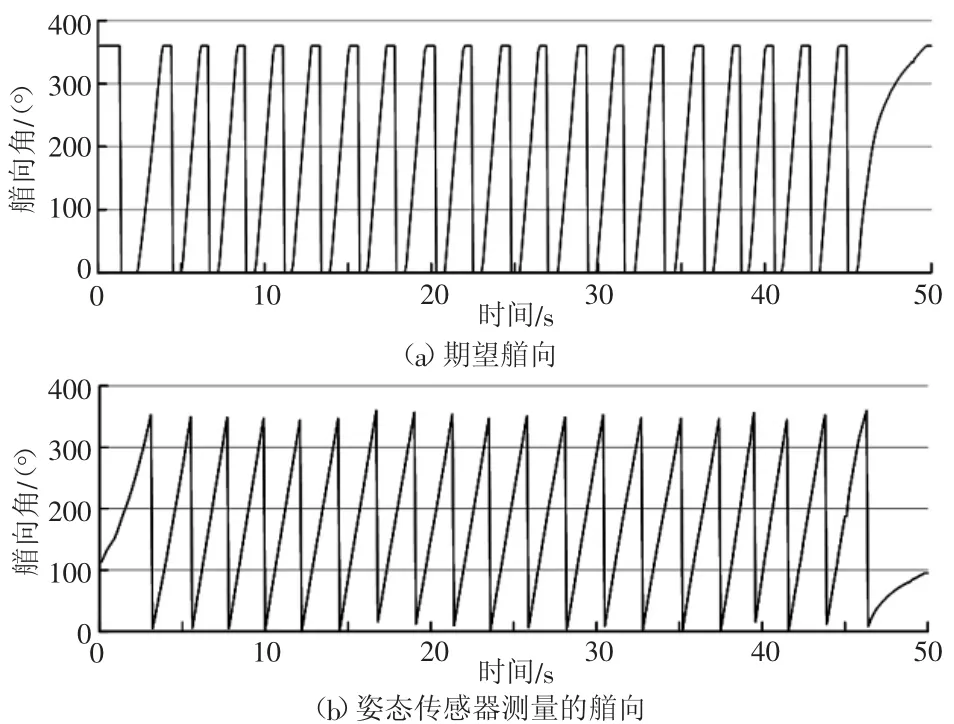
图14 艏向曲线图

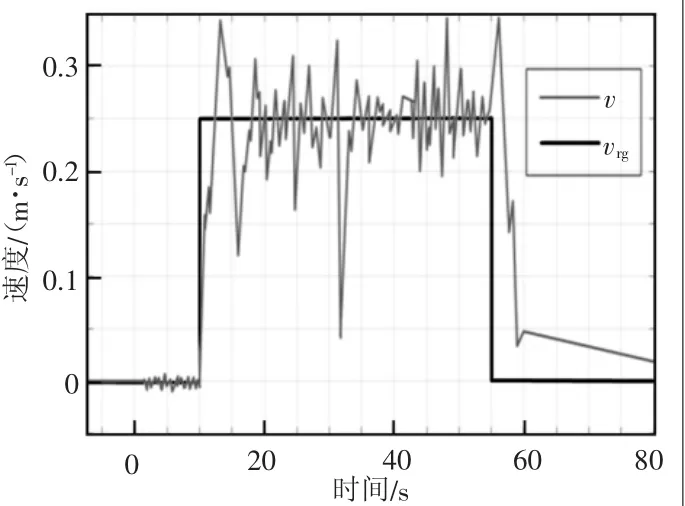
图15 速度曲线图

3 结论

在分析2种全向轮的单轮运动特性和多轮组运动特性后，本文综合分析了它们的优缺点，结合火炬传递应用场景设计了四OMIN全向轮移动平台，该移动平台实现了火炬传递机器人的全方位移动的功能，而且结构简单，运动控制灵活。充分发挥了其在冰面应用环境下的独特优点。尤其在冬奥会火炬传递距离由最初的50 m缩短到10 m后，充分展现了其高效率的旋转特性。通过实物成果的展示，验证了设计理论的合理性及方案的可行性与可靠性。当仿冰壶火炬传递机器人手持燃烧火炬，沿冰壶赛道旋转滑入冰洞口，让生生不息的奥运圣火阶次传递，彰显了奥运与科技的结合。