量子贝叶斯算法的金融应用

2023-09-15葛志斌

银行家 2023年8期

刘越葛志斌

科技的发展给人类的生活带来了极大的便利，从传统计算机的硬件提升到量子计算机的研发应用，迎来了新一轮的算力革命。与此同时，随着国内外金融市场的发展，涌现了大量需要处理的复杂金融数据和大量应用复杂模型的场景，传统计算机硬件的摩尔定律也即将失效，量子计算机特有的并行性和纠缠性质能够相对于经典的处理方法带来平方级加速甚至是指数级加速，这意味着量子计算机的有效应用将给金融领域带来全新的机遇与挑战。本文对传统贝叶斯网络进行改进，构建对应的量子模型，进行相应的流动性风险评估，以期促进金融科技和算法的发展。

量子计算发展历程

人类历史上的第一次量子革命可以追溯到1900年，普朗克用量子论解释黑体辐射问题。在随后的三十多年里，经过爱因斯坦、玻尔、泡利、薛定谔、波恩、海森堡等众多著名物理学家对量子规律的不懈探索，量子力学的物理大厦逐步建立起来。第一次量子革命中量子力学原理的发现，不仅改变了人类对物质世界的看法，而且直接催生了现代信息技术，推动了量子物理应用到电子、计算和通信领域的几乎所有产品和技术。例如，1947年发明的晶体管，利用隧道效应构成了当今数字世界的基础；基于光电效应的光电管与利用光和物质相互作用的激光器，在通信等很多领域都有应用；发光二极管以及包括核磁共振成像在内的许多医学成像方案，也依赖于各种量子效应；基于量子力学构建的原子钟，为全球定位系统奠定了基础。

20世纪80年代以来，人类进入了以量子信息技术为代表的第二次量子革命，实现了量子态主动调控和操纵的巨大飞跃，即控制单个量子物体 (原子、电子、光子)，同时也实现了量子叠加和纠缠。第二次量子革命涵盖了量子物理和量子信息科学在计算、通信、传感等方面的各种创新应用，极大改善了人类数字世界的性能和安全性。量子计算以量子力学的叠加态、非局域纠缠态及量子相干性为基础，利用量子特性进行计算的好处是能够提高运算速度并确保信息和通信安全。量子通信在原理上可以提供无条件安全的通信，既包括应用纯量子原理的量子通信，如量子隐形传态，也涉及将量子原理与经典通信和加密技术结合，如量子密码学。量子传感则利用了量子叠加态和量子纠缠态对于环境变化的异常敏感性，来制造超精确超灵敏的传感器件。

目前，量子计算硬件的技术路线“百花齐放”，主流路线包括超导、半导体量子点、离子阱、光量子、NV色心、拓扑量子、中性原子等多个方向。每种硬件技术路线都有各自的优势和劣势，仍处于并行发展和开放竞争的状态，且尚未出现融合收敛趋势。此外，不同技术路线的量子硬件性能指标如比特数、比特连通性、操纵及门保真度、相干时间等都有所差异，但各种路线的关键指标不断取得新的突破。在全球范围内，各种量子计算的软件技术也随着硬件不断发展且迭代活跃。量子计算软件研发门槛相对较高，仍处于初期发展阶段，开放和开源化是主要发展趋势。

量子金融发展历程

量子计算在金融领域的应用发展十分迅速。在产业现状方面，量子计算头部公司获得了大量的资金支持和资本青睐，投融资的规模也不断增加。量子计算初创公司近年来也不断涌现，一部分公司也开始登陆纳斯达克等交易所。量子计算的产业链逐渐呈现出融合的趋势，产业链上下游公司之间的合作也更加密切频繁。国内外金融巨头纷纷与科研院所和量子计算公司开展密切合作，诞生了很多合作成果。越来越多的量子金融算法研究，如量子蒙特卡洛模拟、量子组合优化及量子机器学习等开始深入实际问题，并不断获得新的突破。量子金融广泛涉及了券商、交易所、银行、保险公司等主要金融机构，涵盖了金融衍生品定价、投资组合优化、银行存贷、证券交易、金融风险控制、量化交易、精算与风险建模、财务分析、资产定价等诸多应用场景；量子金融产品已经从早期的演示示例发展到了与专业金融应用逐渐融合的量子应用云平台、量子金融应用移动端App及专业化的金融程序开发软件等更加丰富、实用和多样化的产品。

贝叶斯网络介绍与量子转化

贝叶斯网络是一种常见的概率图模型，被广泛应用于人工智能与数据挖掘等领域。贝叶斯网络能够帮助我们理解和分析复杂的系统，从而做出准确的预测和决策。

贝叶斯网络主要由节点和边组成。不同于传统的图模型，概率图模型使用节点表示随机变量，使用节点之间的有向边表示节点之间是否存在概率关系。每个节点可以看作一个子节点，子节点会与父节点相连，父节点代表的随机变量会根据概率关系影响其子节点随机变量的取值。这种概率图结构可以清晰反映各个随机变量（节点）之间是否独立，或者以某种关系存在。

贝叶斯网络在使用过程中主要分为两个阶段：学习和推断。其核心是首先利用历史数据，通过一些参数估计方法，学习到节点之间的条件概率，而后使用贝叶斯定理计算出后验概率，然后利用概率关系推断各个变量的状态，完成相应的任务，具体而言：第一，在学习阶段，利用已有的数据来估计节点之间的条件概率。该阶段可以通过点估计或者贝叶斯估计得到。学习阶段的目标是根据数据建立一个准确的贝叶斯网络模型。第二，在推断阶段，使用已经学习到的模型和观测到的证据来计算后验概率。该步骤可以利用贝叶斯定理结合链式法则得到。推断可以帮助我们回答关于系统中变量状态的各种问题，例如，预测未来事件的概率、诊断问题的根本原因或者填补缺失的数据。

贝叶斯网络在许多领域中都有广泛的应用。在医学诊断中，贝叶斯网络可以帮助医生根据症状和测试结果来确定患者可能患有的疾病。在自然语言处理中，贝叶斯网络可以用于语义解析和文本分类。在金融领域，贝叶斯网络可以用于风控模型的构建，该模型可以通过针对不同信贷行为的逾期风险的及时监控和预警完成风险控制。具体实现过程为：贝叶斯网络模型首先通过历史数据，分析得出风险因素的先验概率，再根据最近的数据对先验概率得到后验概率来调整模型，从而找出导致不良贷款、逾期、坏账等问题的风险诱因和影响程度。然而，现有金融领域的贝叶斯应用，由于算力限制，其可构建的网络模型复杂度、运算规模和可在有限时间里完成的计算量均受限。

相应地，贝叶斯网络也被转化到量子版本，研究者在论文中具体地提出了构造的方法和应用场景[1][2]。经典贝叶斯网络中的学习和推断过程转化为了量子概率表示和量子概率推断。

首先，量子贝叶斯网络使用量子态来表示概率分布，用量子比特来表示经典贝叶斯网络中的节点（随机变量）。通过引入量子比特和量子门来实现经典贝叶斯网络到量子贝叶斯网络的结构转化。量子比特可以表示经典贝叶斯网络中的随机变量，而量子门则可以模拟经典贝叶斯网络中的概率依赖关系。经典概率分布的状态被转化为量子态的形式，一般对于一个大小为2的系统使用1个量子比特上的RY门就可以表示。对于一个节点的多个状态，只需要对数级别个数的量子比特进行表示，就会在存储上有指数级加速，这种表示方法称为量子概率表示。量子贝叶斯网络在转化过程中需要考虑到量子计算的特殊性质，如量子叠加态和量子纠缠。这些特性使得量子贝叶斯网络在处理概率关系时具有与经典贝叶斯网络不同的优势。

其次，对于推断过程，通过适当的量子门操作和测量，可以实现对量子贝叶斯网络中的概率进行推断。经典贝叶斯网络是使用贝叶斯定理和链式法则得到的后验概率，而在量子贝叶斯网络中，推断过程主要是由量子态演化和测量组成，量子比特之间的相互作用和测量操作用于更新概率分布的状态。

总而言之，通过量子概率表示和量子概率推断可以将经典贝叶斯网络转化为量子贝叶斯网络。通过引入量子比特和量子门，可以实现经典贝叶斯网络中概率关系的量子描述和推断。

案例分析

本案例针对风险控制问题中的流动性风险进行评估构建对应的量子贝叶斯网络。已知某个银行的变现资产、流动资产、流动负债、长短期存款、总存款、总资产、短期投资、在其他银行的信贷、在中央银行的信贷等等指标数据。

本案例通过人为对数据的理解，和历史经验及历史参考文献中的理论结果来对各个数据之间构建节点关系。由于贝叶斯网络是通过真实量子计算机的量子比特之间的纠缠关系来构建节点之间的单向关系，我们以总债权/总资产和不稳定存款/总负债的单向影响关系举例。假设总债权/总资产单向影响不稳定存款/总负债，且前者高导致后者高的概率为0.988，前者低导致后者也低的概率为0.571。对于初始的节点总债权/总资产假设有一个初始的分布为0.98的概率高和0.02的概率低，由于编码概率的实数性质，所以在编码的时候使用RY门进行编码即可。通过计算可知，初始的概率态编码的角度需要通过计算，也就是找出使得对应的角度值为0.2837。此时对第一个量子比特上的RY门进行角度编码即可。而对于节点对应的单向相关关系可以分别使用实控门（控制节点为1时生效）和虚控门（控制节点为0时生效）进行对应角度的受控旋转，角度的计算和上述相同。于是可以在两个量子比特的节点上得到对应的受控旋转门。具体的线路和角度如图1所示。

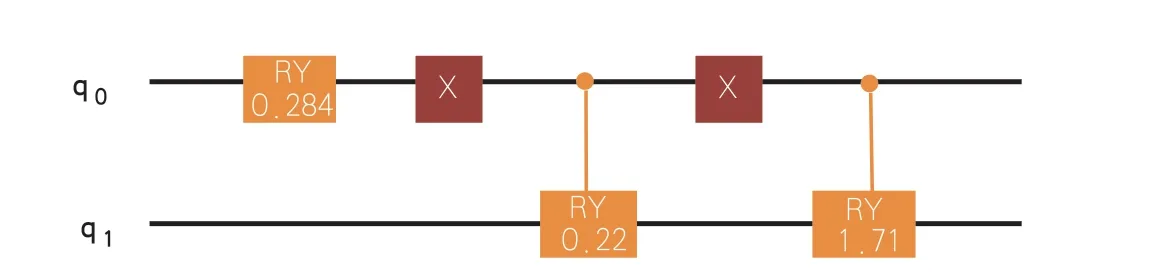
图1 两比特QBN示例

而对于整体的结构按照同样的方法进行扩充，图2给出了具体的因果关系和对应的指标意义.

当线路进行对应的扩充时，只需要在前置的线路中继续连接受控的量子比特即可，由于“X6—X7—X8”是链式的受控的形式，所以只需要对X7对应的量子比特后面继续接入量子线路即可，这就使得前面构建的量子线路是可以重复利用的。图3反映的是对应的具体的扩充后的量子线路。

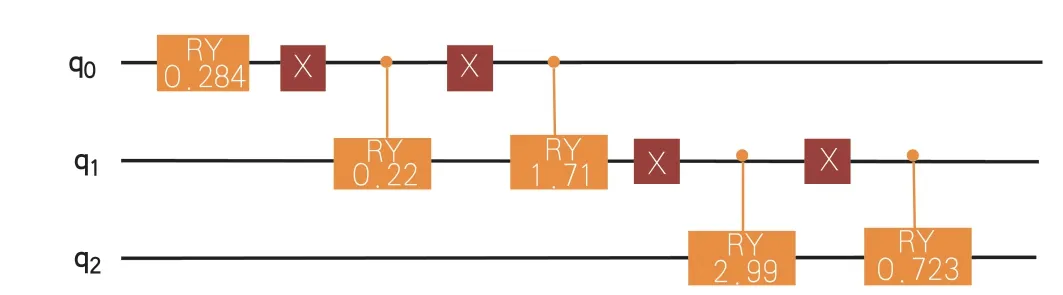
图3 三比特QBN示例

通过这种方法继续完成X1到X10的所有节点构成的线路，再对X10对应的量子比特进行测量就可以完成对应的流动性风险计算。

通过实际的金融数据的输入和角度的编码，我们可以得到在初始节点的概率一定的情况下，X1到X10系统可能出现的最大状态为：|1000000101＞。这也就意味着，该系统最有可能出现的状态为变现比率高、短期投资比率高，其他指标低的情况，而如果我们进行每个比特观测统计测量，得到了10个量子比特对应的具体每个比特的概率测量结果，详见表1。