颗粒阻尼器耗能特性及振动抑制研究

邵敏强 宋杰 姚鹏 滕汉东

摘 要：机电控制系统受振动影响易发生故障，严重影响飞行安全，本文通过颗粒阻尼器对机电控制系统进行振动抑制研究，采用离散元仿真方法研究阻尼器的耗能变化规律与振动幅值、振动频率和颗粒数量的影响关系，并通过BP神经网络对颗粒阻尼器耗能数据进行训练和预测；通过机电控制器的随机振动试验，验证离散元仿真结论与BP神经网络预测模型的准确性。结论表明，离散元仿真在振动频率20～40Hz、激励幅值2～16mm范围内，其他条件一定时，阻尼器耗能随频率和幅值的增大而增大，随颗粒填充率先增大后减小，在57%～70%填充率范围内具有最佳耗能效果；在机载系统随机振动试验中，颗粒阻尼器填充率处于30%～90%范围内均表现出较好的振动抑制效果。仿真和试验结果对颗粒阻尼器在机电控制系统中进一步应用具有指导意义。

关键词：机载设备； 颗粒阻尼器； 离散单元法； BP神经网络； 随机振动

中图分类号：TH703 文献标识码：A DOI：10.19452/j.issn1007-5453.2023.06.011

基金项目： 航空科学基金（20200028052013）

近年来，随着电子技术的发展和智能化水平的提高，由精密的电子元器件和复杂机械结构等组成的机载设备集成化程度和综合性能大幅提高，机载设备对飞机的控制、通信、定位、导航等方面都具有重要作用[1]。飞机运行时产生的随机振动会对机载设备的正常工作造成严重影响，振动问题给机载设备的稳定性及飞机的安全性能带来很大挑战。机载设备的振动机理和振动抑制在航空领域是一个重要的研究课题。

颗粒阻尼技术自提出以来受到广泛的研究，广泛应用于航空、航天、机械、土木等领域，颗粒阻尼器的减振机理主要是颗粒间的摩擦和非弹性碰撞作用造成能量的交换与耗散[2]，减振研究主要通过数值模拟方法与试验方法展开。於为刚等[3]针对航空液压管道的振动问题，通过离散元仿真分析与减振试验发现在一定的输入条件（颗粒大小、填充率）下颗粒阻尼器达到最优的减振效果；P. Veeramuthuvel[4-5]通过大量试验获得颗粒阻尼器参数（颗粒直径、填充率和颗粒密度）的最佳组合，通过神经网络对试验数据进行训练并建立预测模型，预测结果与实际加速度响应相符，验证了随机振动环境下颗粒阻尼器对航天器印刷电路板振动的有效抑制；陈前等[6-7]基于碰撞理论对颗粒阻尼提出计算模型并进行试验研究，从碰撞力学的角度建立颗粒单元的动力学分析模型，计算的损耗因子结果与试验结果有很好的一致性，验证了计算模型的准确性。李来强等[8]利用改进的BP神经网络算法对颗粒碰撞振动阻尼进行了预测，通过对阻尼器的激振频率、填充率和振幅有效值等参数进行仿真，得到了系统在低频阶段颗粒粒度、填充率和振幅有效值之间的关系；徐志凯等[9]基于网格搜索法（GS）的支持向量機（SVM）建立了颗粒运动形态的分类预测模型及其能量损耗的回归预测模型，对颗粒运动形态的分布及其能量损耗的大小进行了预测，很好地揭示了颗粒系统在不同运动形态下的能量耗散变化规律；鲁正等[10]基于离散单元法，建立颗粒阻尼器对多自由度结构的减振控制数值模型，试验结果与数值模拟结果吻合良好，为颗粒阻尼器在土木工程上的应用提供了一条可行的数值分析途径。

颗粒阻尼具有高度的非线性特性，受到的影响因素复杂，如颗粒的材料属性、外形、直径，颗粒的填充率，容器形状以及振动环境等因素相互影响，对减振效果产生不同的影响。在工程应用中，很难对各种因素都加以考虑，一般考虑主要因素对结构的影响，忽略次要因素的影响。

本文主要针对机载机电控制器的振动问题，展开颗粒阻尼器的研究工作，根据仿真与试验结果对颗粒阻尼器进行设计与研究，分析颗粒阻尼的阻尼耗能特性，验证基于颗粒阻尼动力吸振器的减振性能指标，达到提升机载设备的使用性能和使用寿命的目的。

1 颗粒碰撞原理及耗能研究

1.1 离散单元理论模型

颗粒阻尼器内部环境干燥、整洁，颗粒间无黏结，不考虑塑性变形，只考虑颗粒间的碰撞与摩擦耗能，本文采用Hertz-Mindlin无滑动接触模型对颗粒碰撞行为进行分析，法向力基于Hertz接触理论进行计算，切向力基于Mindlin接触理论进行计算，颗粒接触模型如图1所示[11-12]。

颗粒间的接触力计算模型同样适用于颗粒与阻尼器内壁碰撞时的作用力计算，其中阻尼器内壁为平面时半径趋于无穷，等效粒子半径为颗粒半径；其他情况下，根据颗粒间接触力模型进行计算。根据颗粒碰撞基本力学模型，可进一步扩展到多颗粒、颗粒与容器碰撞过程的动力学计算以及由摩擦产生的能量耗散。

1.2 颗粒碰撞耗能

1.3 离散元仿真

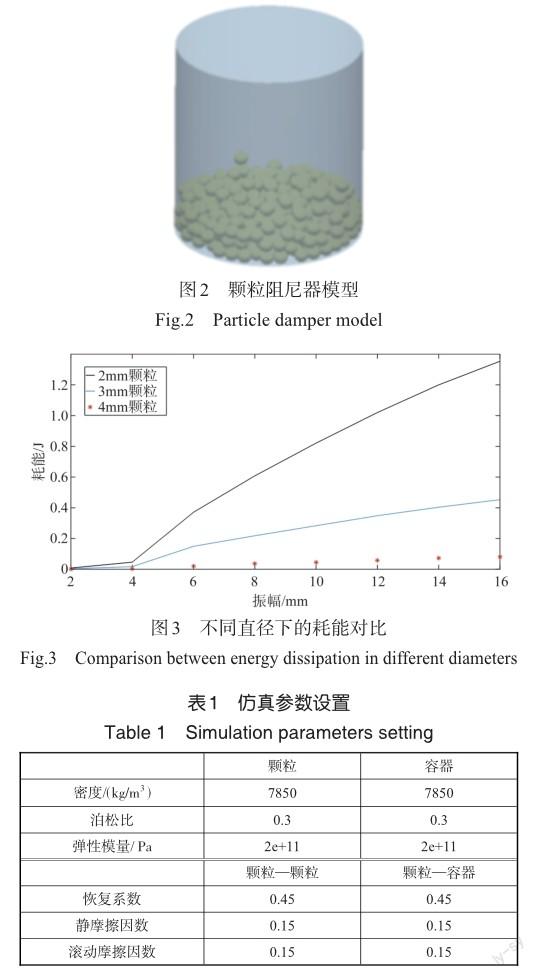
根据颗粒接触碰撞动力学模型和能量耗散规律，结合工程离散元仿真软件（EDEM）进一步开展颗粒碰撞动力学数值模拟，研究颗粒的填充率、激励幅值和频率对系统的耗能影响规律，从而获得高耗能状态下的结构参数设置，为颗粒阻尼器设计提供依据。仿真结构模型如图2所示，阻尼器圆柱体的高度为30mm，内径为28mm，根据阻尼器结构选择合适大小的颗粒进行仿真。分别选用直径为2mm、3mm和4mm的颗粒进行仿真分析，在相同填充率下分析颗粒直径对耗能的影响，耗能结果如图3所示，2mm直径颗粒耗能效果最好，4mm直径颗粒效果最差，3mm直径颗粒耗能效果介于两者之间，综合考虑耗能效果和仿真计算量，采用3mm直径颗粒进行不同颗粒数量、外激励频率和幅值情况下的离散元仿真研究，当颗粒数量为700时将容器填满，填充率接近100%，颗粒和容器采用相同的材料，材料参数和接触参数见表1，根据离散单元法进行仿真，时间步长取Rayleigh时间步的30%，设置为4.88×10-7s，仿真时长为1s。

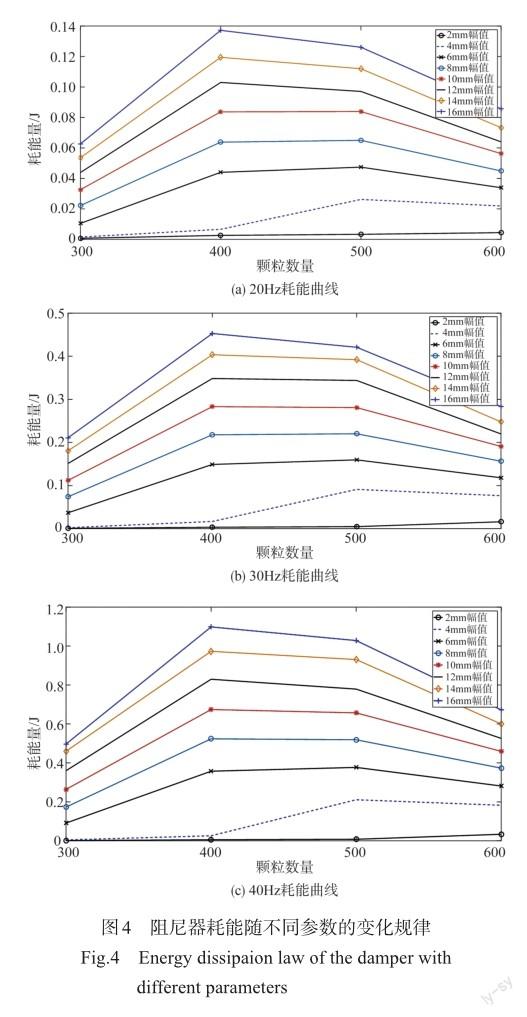
离散元仿真得到20～40Hz频率下不同颗粒数量与振动幅值的耗能变化规律，如图4所示。

在颗粒数量和激励频率不变的情况下，通过调节振动幅值，阻尼器能量耗散值随振动幅值的增加而增大；在颗粒数量和激励幅值不变的情况下，阻尼器耗能随频率增加呈递增趋势；当激励幅值和频率一定时，改变阻尼器的颗粒数量，阻尼器耗能随颗粒数量的增加呈先增大后减小的变化趋势，将颗粒数量转换为相对于容器的填充率时，在57%～ 70%填充率范围内产生最佳耗能效果，在实际应用中以该填充率作为阻尼器设计的依据。

2 BP神经网络耗能预测与试验验证

2.1 离散单元理论模型

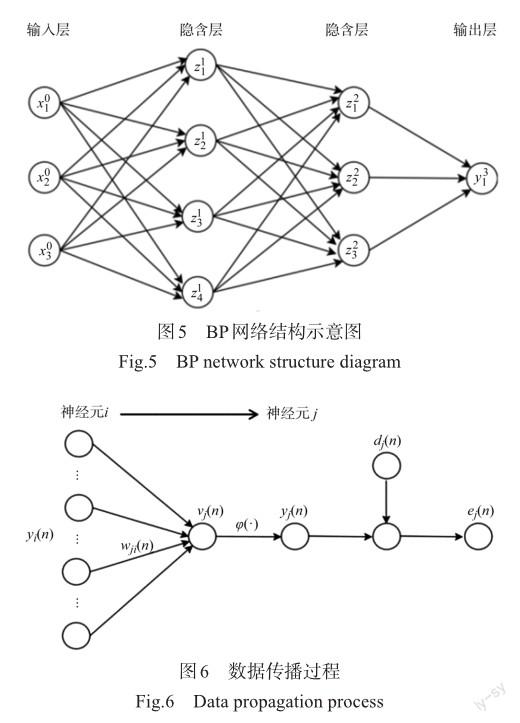
由于颗粒阻尼器动力学性能仿真计算量大、耗时长，为提高阻尼器设计效率，对耗能未知的参数状态进行估计，获得各种参数取值情况的耗能结果，结合神经网络构建估计模型，采用有限计算数据进行模型训练，获得有效的颗粒阻尼器耗能估计神经网络模型。神经网络误差反向传播算法的结构如图5所示，该算法由前向传播和反向传播组成。前向传播中，输入矢量通过前向传播，产生一个输出矢量，若输出与期望相差较大，则转入反向传播；在反向传播中，根据网络的目标响应减去实际响应而产生误差信号对权值进行调整，误差信号通过反向传播，调整权值使得网络的实际响应从统计意义上接近目标响应[15]。

2.2 预测模型

通过离散元仿真得到振动频率分别为20Hz、30Hz、40Hz情况下，振动位移幅值的范围分别为2mm、4mm、6mm、8mm、10mm、12mm、14mm、16mm，颗粒填充数量变化范围为300、400、500、600下阻尼器的耗能数据，离散元仿真得到96组耗能数据，将耗能数据中的75%划分为训练集，对网络模型进行训练，获得符合精度要求的预测模型；25%划分为测试集，对训练好的神经网络模型进行验证。为避免人为因素的干扰与数据数量级带来的误差，采用随机选择的方式对样本进行训练并对训练数据进行[-1，1]范围内的归一化处理。

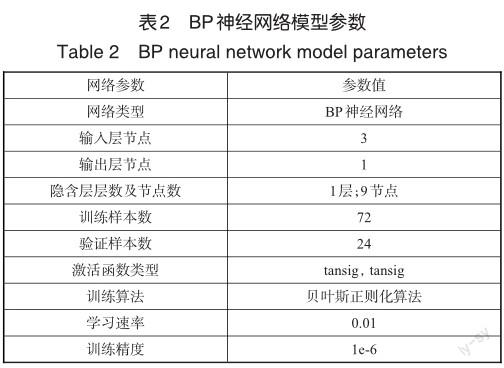
本文神經网络的输入维度为3，即颗粒填充率、激励幅值、激励频率；输出维度为1，即能量耗散值；隐含层层数越多意味着更复杂的拟合函数，同时也会带来过拟合的现象，隐含层节点的选取根据经验公式（21）所示做出选择

其中，h为隐含层节点数目，m为输入层节点数，n为输出层节点数，a为1～10的调节常数。

隐含层传递函数选用双曲正切函数，BP神经网络模型参数见表2。神经网络对训练样本数据的拟合相关性如图7所示，其中实际值和预测值都经过归一化处理，图7（a）表示神经网络从训练数据中选取85%的数据用作训练，图7（b）表示训练数据中的15%用作测试网络拟合的性能，图7（c）表示网络对整个训练数据预测值与实际值拟合的相关性。网络预测模型与实际值之间能达到较好的一致性，网络对训练样本具有较高的拟合程度，可用于对验证样本的预测。通过对验证样本数据进行预测，预测结果与实际值拟合程度如图8所示，两者具有较好的一致性。

根据神经网络预测模型进一步估计最佳耗能所对应的阻尼器填充率，选择激励频率为30Hz、幅值为10mm的状态进行估计，结果如图9所示，当颗粒填充率为63%时阻尼器达到最大耗能，为0.386J。

3 颗粒阻尼器在机电控制器上的应用研究

3.1 机电控制器与试验条件

根据机电控制器安装空间和仿真获得的颗粒填充率设置参数，设计符合机电控制器应用的颗粒阻尼器。机电控制器的三维模型如图10所示，主要由安装支架和机箱组成，机箱内部布置有电路板及连接插口等电子零部件。安装支架及机箱主体均采用6061-T6铝合金材料；机箱内部印制电路板的材料为FR-4。

试验条件为宽带加窄带随机振动，其功率谱密度（PSD）变化规律曲线如图11所示，其中窄带的中心频率分别为 f1， f2， f3， f4 ，频率值分别为107.5Hz，215Hz，322.5Hz，430Hz，窄带带宽为中心频率的 ±5%；宽带激励的频率范围为15～2000Hz，计算公式如式（21）所示

3.2 机电控制器动态特性试验

3.2.1 机电控制器模态试验

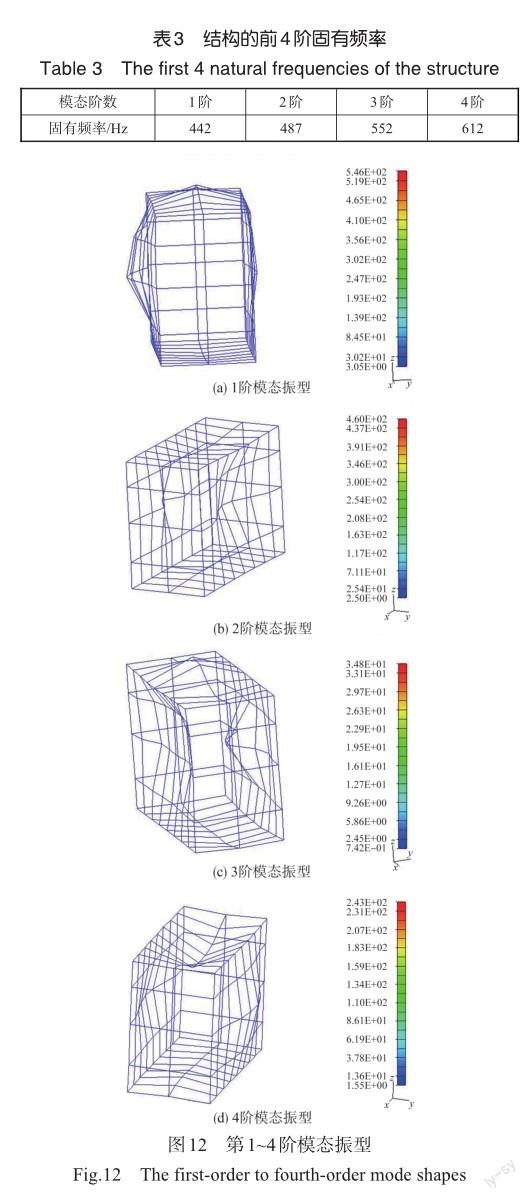
为进一步确定阻尼器安装位置，对机箱的固有动态特性进行测试。通过橡皮绳悬挂，模拟机箱自由约束状态，采用锤击法进行模态试验，移动加速度传感器测量机箱的各测点响应，信号采集和频响函数处理由晶钻Spider-80动态信号分析仪实现。经测量计算，获得机电控制器前4阶固有频率见表3，模态振型如图12所示。

根据前4阶振型，可知机箱壳体在侧面板中心位置处于振型的峰值位置，相对其他位置该处变形最大，在该位置安装阻尼器能够起到较好的振动抑制效果。

3.2.2 机电控制器随机振动试验

将机电控制器安装在振动台上进行随机振动试验，以加速度总均方根值（Grms）为8g的随机激励作为输入进行振动试验，振动台实际输入Grms为8.41g，结构响应点的PSD曲线如图13所示，响应点的Grms为21.34g，响应与输入的比值为2.54，结构的响应明显放大，主要频率点响应峰值与对应的频率见表4。

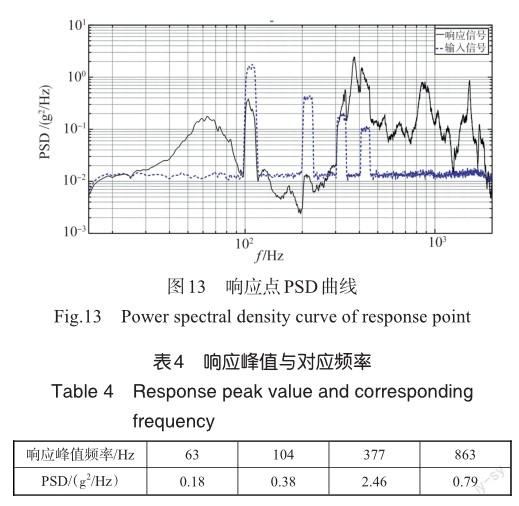
对图13和表4进行分析，相比基础激励，在前两个窄带范围内测点响应出现减小的现象，后两个窄带范围内响应功率谱密度表现出放大，且在30～90Hz以及300Hz以上频段，结构响应功率谱密度均出现明显放大现象。

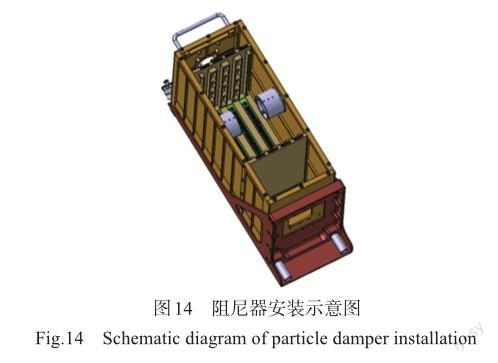
对机电控制器进行振动抑制研究，根据模态试验结果与随机振动响应分析，考虑机箱的实际结构及阻尼器的安装空间，在机箱两侧面安装颗粒阻尼器，安装位置如图14所示，试验时通过502胶水将阻尼器与机箱黏结，进行减振研究。

3.3 颗粒阻尼减振试验

通过机电控制器的随机振动试验验证颗粒阻尼器在不同填充率下的减振效果，随机振动试验仪器设备如图15所示，振动测试试验由振动台控制主机输入外激励信号，加速度传感器布置在转接结构件上测量振动台的实际振动信号，并在试验件上布置加速度计测量结构的振动响应信号，对采集的数据进行处理，分析阻尼器的减振效果。

以Grms为8g的随机激励作为输入，通过对2mm直径颗粒进行随机振动试验，研究阻尼器颗粒填充率对结构的减振效果，加速度响应Grms随颗粒阻尼器填充率的变化曲线如图16所示。

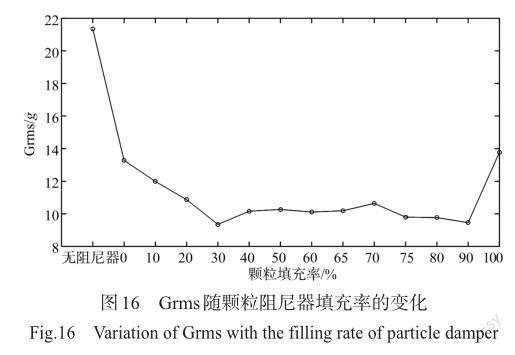
在随机振动条件下，无颗粒阻尼器时结构测点响应和输入总均方根比值为2.54，安装阻尼器的情况下，改变颗粒的填充率，结构监测点响应和输入总均方根比值随着颗粒填充率变化表现出先减小后增大的现象。填充率在0～30%时，输出、输入总均方根比值急剧减小；当填充率为30%时，输出、输入总均方根比值为1.11，达到最优减振效果，与无阻尼器的情况相比，测点响应衰减率达到56%以上；在填充率为30%～90%时，输出、输入总均方根比值处于1.11和1.27之间，变化趋势平缓；当填充率为0和100%时，无颗粒碰撞耗能，此时阻尼器对整体结构起到附加质量的效果，对原结构固有频率产生一定影响[16]，且振动抑制效果明显弱于其他填充率情况。试验结果表明，颗粒阻尼在机电控制器减振中发挥有效的能量耗散作用。

4 结论

本文通过对颗粒阻尼器的动力学性能进行研究，获得颗粒阻尼器摩擦和非弹性碰撞情况下的耗能特性，根据仿真分析结果建立多参数影响下的颗粒阻尼器耗能预测模型，进一步结合机电控制器开展振動抑制试验研究，有效验证颗粒阻尼器的动力学特性和耗能规律。通过研究，可以得到以下结论：

（1）采用离散单元法进行颗粒碰撞动力学研究，建立碰撞模型与耗能模型。通过EDEM离散元仿真颗粒阻尼器在不同的激励频率、激振幅值以及不同颗粒数量情况下的系统耗能变化规律。

（2）针对颗粒阻尼器非线性特点，采用BP神经网络方法建立颗粒阻尼器能量耗散和激励频率、幅值和颗粒填充率之间的对应关系，将耗能数据通过神经网络模型训练，获得有效的能量耗散预测模型，为颗粒阻尼器的设计提供指导。

（3）在随机振动试验中，通过颗粒阻尼器对机电控制器的减振试验研究，阻尼器减振效果随填充率的变化趋势与仿真结果一致，且试验中颗粒填充率在30%附近达到最佳振动抑制效果，在填充率处于30%～90%范围时输出、输入总均方根比值接近。这表明颗粒阻尼在机电控制器减振中发挥有效的能量耗散作用。

参考文献

[1]醋强一，成鑫，畅凡，等. 机载电子设备温循寿命试验方法探讨[J]. 航空科学技术，2022，33 （6）： 86-89. Cu Qiangyi， Cheng Xin， Chang Fan， et al. Discussion on exper‐imental method of temperature cycle life for airborne electron‐ic equipment[J]. Aeronautical Science & Technology， 2022， 33（6）： 86-89. （in Chinese）

[2]闫维明，王宝顺，黄绪宏. 颗粒阻尼器的研究进展及其在土木工程中的应用展望[J]. 土木工程学报，2020，53（5）： 32-41. Yan Weiming， Wang Baoshun， Huang Xuhong. Research prog‐ress of particle damper and its application prospect in civil en‐gineering[J]. China Civil Engineering Journal， 2020， 53（5）： 32-41. （in Chinese）

[3]於为刚，陈果，刘彬彬，等. 飞机管道颗粒碰撞阻尼器设计与试验验证 [J]. 航空学报，2018，39（12）： 401-413. Yu Weigang， Chen Guo， Liu Binbin， et al. Design of a particle damping absorber and experimental study on vibration damp‐ing of pipe[J]. Acat Aeronautica et Astronautica Sinica， 2018， 39（12）： 401-413. （in Chinese）

[4]Veeramuthuvel P， Shankar K， Sairajan K K. Vibration suppres‐sion of printed circuit boards using an external particle damper[J]. Journal of Sound and Vibration， 2016， 366： 98-116.

[5]Veeramuthuvel P， Shankar K， Sairajan K K. Experimental in‐vestigation of particle damper-based vibration suppression in printed circuit board for spacecraft applications[J]. Proceedings of the Institution of Mechanical Engineers， Part G Journal of Aerospace Engineering， 2016， 230（7）： 1299-1311.

[6]段勇，陳前，林莎. 颗粒阻尼对直升机旋翼桨叶减振效果的试验[J]. 航空学报，2009，30（11）： 2113-2118. Duan Yong， Chen Qian， Lin Sha. Experiments of vibration re‐duction effect of particle damping on helicopter rotor blade[J]. Acat Aeronautica et Astronautica Sinica， 2009， 30（11）： 2113-2118. （in Chinese）

[7]王青梅，陈前. 基于碰撞理论的颗粒阻尼计算模型及试验研究[J]. 振动、测试与诊断，2007，27（4）： 300-303. Wang Qingmei， Chen Qian. Computational model based on col‐lision theory and experimental study on particle damping[J]. Journal of Vibration， Measurement & Diagnosis，2007， 27（4）： 300-303. （in Chinese）

[8]李来强，王树林，李生娟，等. 基于模拟退火改进的神经网络算法在颗粒碰撞阻尼研究中的应用[J]. 振动与冲击，2010，29（3）： 89-90，112. Li Laiqiang， Wang Shulin， Li Shengjuan， et al. Particle damp‐ing analysis using neural network based on improved simulated annealing method[J]. Journal of Vibration and Shock， 2010， 29（3）： 89-90，112. （in Chinese）

[9]徐志凯，尹忠俊，韩天. SVM颗粒运动形态及其能量耗散的预测分析[J]. 实验室研究与探索，2020，39（1）： 59-64，82. Xu Zhikai， Yin Zhongjun， Han Tian. Prediction of particle motion modes and energy dissipation based on SVM[J]. Research and Ex‐ploration in Laboratory， 2020， 39（1）： 59-64，82. （in Chinese）

[10]鲁正，吕西林. 颗粒阻尼器减震控制的数值模拟[J]. 同济大学学报（自然科学版），2013，41（8）： 1140-1144，1184. Lu Zheng， Lyu Xilin. Numerical simulation of vibration con‐trol effects od particle dampers[J]. Journal of Tongji University（Natural Science）， 2013， 41（8）： 1140-1144，1184. （in Chinese）

[11]Zhou Y C， Wright B D， Yang R Y， et al. Rolling friction in the dynamic simulation of sandpile formation[J]. Physica A： Statis‐tical Mechanics and Its Applications， 1999， 269（2-4）： 536-553.

[12]孙其诚，王光谦. 颗粒物质力学导论[M]. 北京：科学出版社，2009. Sun Qicheng， Wang Guangqian. Introduction to the mechanics of particulate matter[M].Beijing： Science Press，2009. （in Chinese）

[13]姚冰. 顆粒阻尼建模仿真及工程应用[D]. 南京：南京航空航天大学，2013. Yao Bing. Modeling and simulation of particle damping and its engineering applications[D]. Nanjing： Nanjing University of Aeronautics and Astronautics， 2013. （in Chinese）

[14]金栋平，胡海岩. 碰撞振动与控制[M]. 北京：科学出版社，2005. Jin Dongping， Hu Haiyan. Collision vibration and control [M]. Beijing： Science Press， 2005. （in Chinese）

[15]贲可荣，张彦铎. 人工智能[M]. 3版. 北京：清华大学出版社，2018. Ben Kerong， Zhang Yanduo. Artificial intelligence[M]. 3rd edi‐tion. Beijing： Tsinghua University Press， 2018. （in Chinese）

[16]冯志杰，肖慧婷，杨永锋. 基于机构随机振动分析的载荷谱非参数上限统计归纳方法对比研究[J]. 航空科学技术，2022，33 （7）： 120-126. Feng Zhijie， Xiao Huiting， Yang Yongfeng. Comparative study on non-parametric upper limit statistical induction of load spec‐trum based on random vibration response of mechanism[J]. Aeronautical Science & Technology， 2022， 33 （7）： 120-126. （in Chinese）

Study on Energy Dissipation Characteristics and Vibration Suppression of Particle Damper

Shao Minqiang1， Song Jie1， Yao Peng2， Teng Handong1

1. State Key Laboratory of Mechanics and Control for Aerospace Structures， Nanjing University of Aeronautics and Astronautics，Nanjing 210016， China

2. AVIC Jincheng Nanjing Engineering Institute of Aircraft System，Nanjing 211106， China

Abstract： Mechanical and electrical control system is prone to failure due to vibration， which seriously affects flight safety. In this paper， particle damper is used to study the vibration suppression of electromechanical control system. Discrete element simulation method is used to study the energy dissipation law of the damper and the influence on vibration amplitude， vibration frequency and particle number. BP neural network is used to train and predict the energy dissipation data of the particle damper. Through random vibration test of electromechanical controller， the accuracy of discrete element simulation conclusion and BP neural network prediction model is verified. The results show that discrete element simulation is performed in the range of vibration frequency 20～40Hz and amplitude 2～16mm. And when other conditions are fixed， the energy dissipation of the damper increases with the increase of frequency and amplitude， the energy dissipation of the damper increases first and then decreases with the particle filling. The best energy dissipation effect is obtained at the filling rate of 57%～70%. The particle damper has a good vibration reduction effect when the filling rate is between 30% and 90%. Combined with BP neural network energy dissipation prediction model and experiment of particle damper， it can provide guidance for the design and application of particle damper effectively.

Key Words： airborne equipment； particle damper； discrete element method； BP neural network； random vibration