减速器内部金属屑运动仿真分析

张祺祥 ，韦 坤 ，王泓林 ，陆凤霞

（1.中国航空发动机集团有限公司，北京 100097；2.南京航空航天大学直升机传动技术重点实验室，南京 210016）

0 引言

直升机减速器内轴承发生异常磨损时会产生金属屑，通过高速旋转的齿轮搅动油气使其向底部流动，若其能被机匣底部的信号器吸附及报警，可实现减速器故障监控，因此亟需研究金属屑在中减内部固-液-气的运动状态及附加力对其的影响规律。

Ran 等[1]分析了粒子的边界层特征和对粒子的作用力，应用拉格朗日方法提出了气固旋转流中粒子运动的3 维数学模型，表明在旋转边界层中离心力和萨夫曼升力对颗粒与气固旋转流的分离过程中起着重要作用；Mithun 等[2]提出了一种三相流完全可压缩模型和浸入边界模型，用于预测不可凝气体（Non-Condensable Gas,NCG）存在下2 维齿轮泵发生的空化现象；Zhang 等[3]提出了一种多尺度的离散相模型（Discrete Particle Mode , DPM）和直接数值模拟法（Direct Numerical Simulation,DNS）耦合方法DPM-DNS，表明采用DPM-DNS 计算得到的合成相力分布和浓度分布与采用得到的DNS 基本相同，计算速度较DNS 高30 倍以上，但远低于DPM；喻泽雄[4]提出了由高斯光诱导的温度梯度导致的表面张力系数梯度，研究了表面张力梯度对微粒的驱动特性；赖科等[5]以毫米级球形颗粒为例，获得颗粒在流场中的运动轨迹，并分析了颗粒在旋转流场中的受力情况，表明离心力和科氏力是颗粒在旋转流场中运动的主要影响因素；夏铖[6]基于计算流体力学-离散元法（Computational Fluid Dynamics-Discrete Element Method, CFD-DEM）耦合方法，选取欧拉-拉格朗日法计算液固两相流运动，对比分析了不同形态和体积分数的颗粒在2 级混流泵内部的运动规律来得到颗粒的流动特性；Drew 等[7]推导了虚拟质量加速度的一般形式，并通过试验确定了虚质量力的计算公式；黄社华等[8-10]针对任意流场内稀疏颗粒非线性运动方程，采用积分变换方法对其进行解析，并提出了以P（EC）k多步法差分格式为基础的数值计算方法；李振中等[11]应用理论和数值方法计算稀疏固气两相湍流中的颗粒所受各种相间力，同时考虑剪切升力和旋转升力，表明除曳力和重力外，在主流和翼展方向上Basset 力较重要，而在壁面法向上拖曳力、剪切升力和Basset 力均重要；Yang 等[12]结合动网格法（dynamic mesh，DM）和DPM 模型计算颗粒运动轨迹和分布，结果表明颗粒均呈离心运动趋势，粒子的平均运动速度与齿轮转速和中心距呈非线性正、负关系；陈有斌等[13]研究了旋流场作用下固相颗粒的动力学特性，并进行粒子图像测速（Particle Image Velocimetry, PIV）流场测试分析，研究固相颗粒的运动轨迹、停留时间及受力特点。

目前针对颗粒的运动分析多以颗粒的运动特性仿真分析为主，缺少通过颗粒受力的运动方程揭示运动机理研究。本文根据颗粒受力平衡方程，基于单向数值计算方法，获得减速器内颗粒的运动轨迹，采用多相流模型（Volume of Fluid, VOF）和DPM 相结合的CFD 仿真方法，计算双向耦合作用下的颗粒运动轨迹；对比验证VOF-DPM 耦合模型的正确性，并利用CFD 仿真对比分析不同附加力对颗粒运动轨迹的影响。

1 VOF-DPM 耦合模型验证

1.1 颗粒受力方程

根据牛顿第二定律得到颗粒的载荷平衡方程

式中：mp为颗粒质量，kg；u为连续相的速度，m/s；up为颗粒速度，m/s；ρ为连续相的密度，kg/m3；ρp为颗粒的密度，kg/m3；F为附加力，N；（u-up）/τr为颗粒受到的流体阻力（曳力），N；τr为颗粒的弛豫时间，s

式中：μ为连续相的分子粘度，Pa·s；dp为颗粒直径，m；Cd为阻力系数；Re为相对雷诺数，其定义为

式中：a1、a2、a3为常数，在不同雷诺数范围内有不同的值[14]

此外，颗粒旋转对其在流体中的运动状态也有着一定影响，尤其对于高转动惯量的颗粒，影响更为明显。为考虑颗粒的旋转，需求解关于角动量的常微分方程

式中：Ip为颗粒转动惯量，kg·m2；ωp为颗粒角速度，rad/s；ρf为流体密度，kg/m3；Cω为旋转阻力系数；T为作用在颗粒上的力矩，N·m；|Ω|为相对颗粒-流体角速度，rad/s

对于球形颗粒，其转动惯量Ip为

由于DPM 模型基于拉格朗日坐标系，将颗粒视为质点，忽略颗粒间的相互作用力、碰撞、摩擦、变形等，通过式（1）从流场中的受力即可得出其加速度，根据加速计算速度，最后得出颗粒在流场中的运动轨迹。

1.2 编程计算

根据颗粒的受力方程，编程计算颗粒的运动轨迹及运动速度，为节省计算成本，未添加任何附加力，则式（1）简化为

每次迭代时需判断Cd大小，尤其是在空气与润滑油的交界面，此时连续相的粘度与密度均会发生突变。此外还需判定当前时刻颗粒的空间位置是否撞击到箱体或齿轮壁面，如果撞击到则需变换颗粒的速度矢量继续求解。计算流程如图1所示。

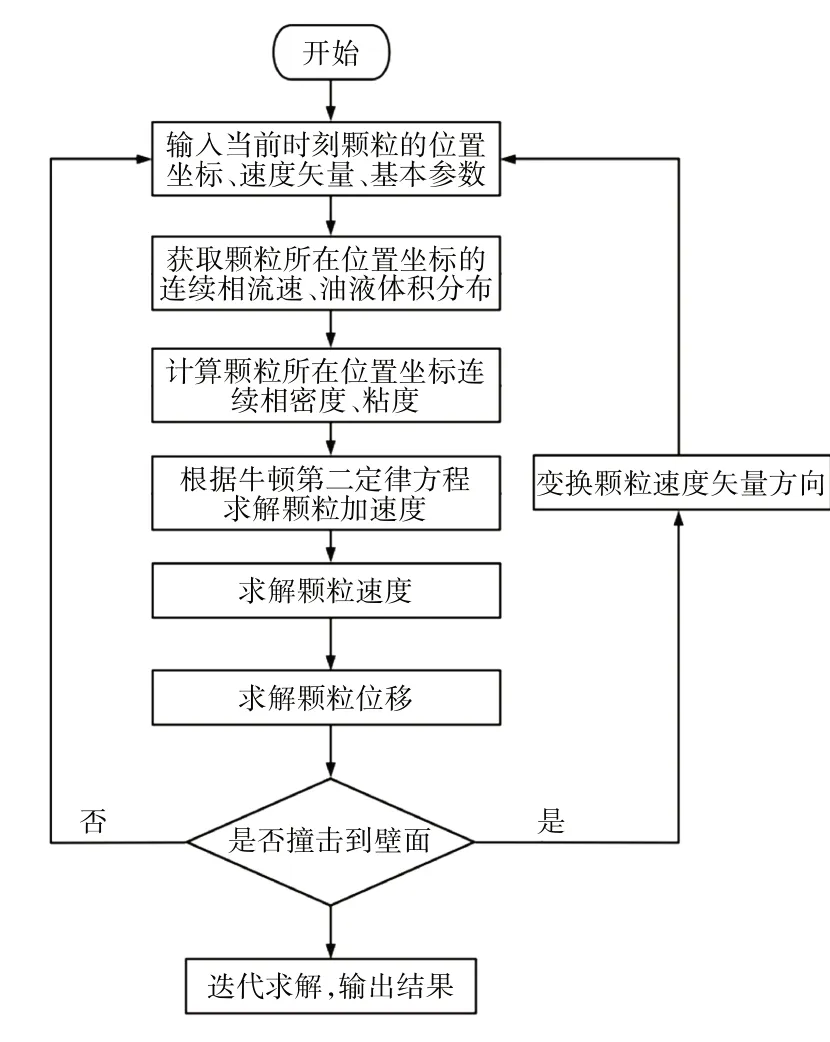
图1 计算流程

1.3 CFD仿真

由于3 维减速器中颗粒运动轨迹复杂，本文以简化的2 维减速器进行分析。建立齿轮箱平面如图2 所示。齿轮箱长434 mm，高300 mm，压力出口宽20 mm，对其划分非结构化网格以适应复杂流动状态，以压力出口的质量流量为监测量，经过网格无关性验证，网格数量最终确定为18742，网格质量最大偏斜度为0.5812，符合CFD仿真计算标准。

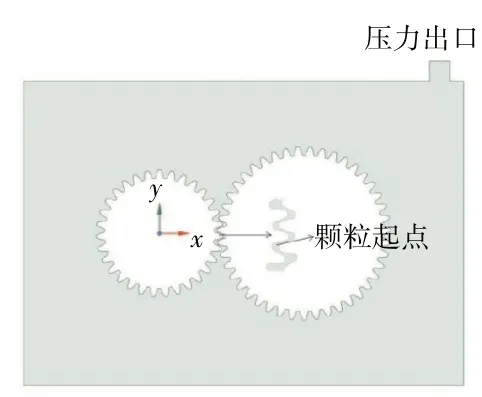
图2 齿轮箱平面

齿轮模数、齿数、转速、浸油深度、颗粒物性参数等齿轮及滑油的主要参数设置见表1。

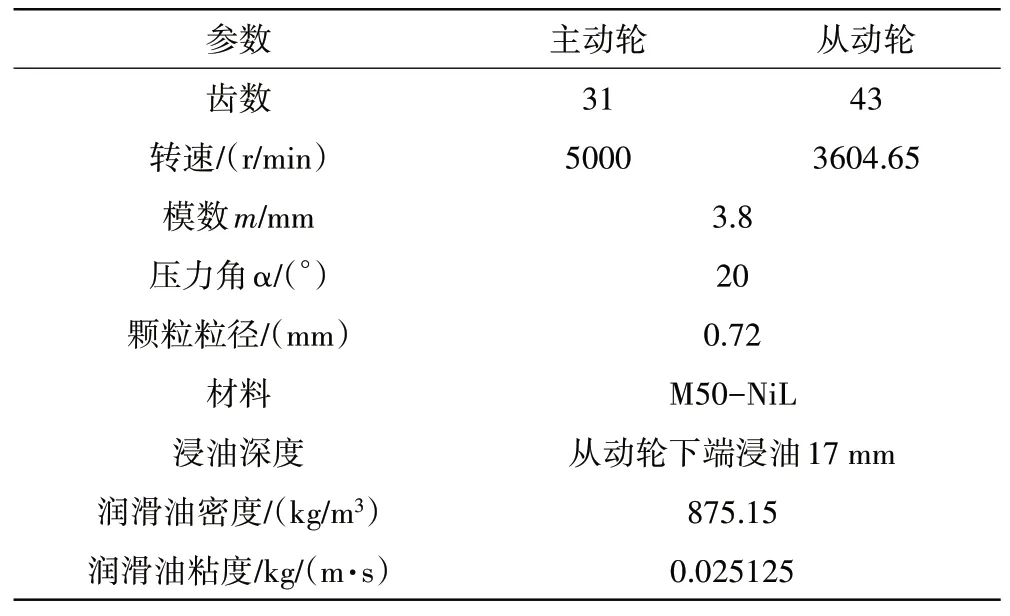
表1 齿轮及滑油的主要参数

为更好研究颗粒的运动状态，在齿轮啮合处预置单个颗粒，流场计算模型初始状态如图3 所示。开启双向耦合模型，时间步长设为5×10-6s，计算0.1 s 即主动轮转动约10圈。

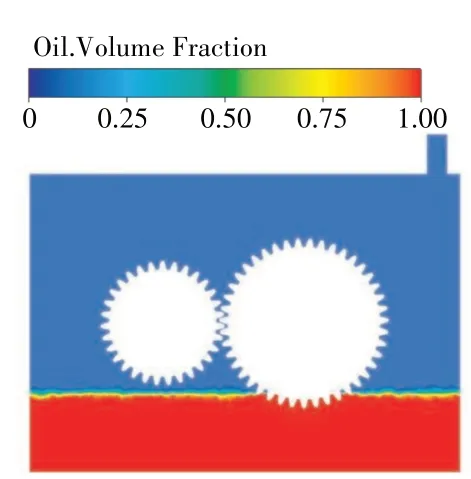
图3 流场计算模型初始状态

1.4 对比验证

应用编程计算方法与CFD 方法分别计算颗粒运动轨迹，如图4（a）所示。从图中可见，在初始时刻颗粒从齿轮啮合处至进入油液中，2 种方法计算的颗粒轨迹极为接近；在颗粒射入油液中后，在浮力和流体曳力的综合作用下，颗粒轨迹有2 处上浮的位置，而CFD 方法仅有1 处（图中黑色方框处），而其余位置轨迹误差很小；待颗粒随齿轮转动再次飞出油液后，编程计算方法计算的颗粒飞出角度略大，导致其后续运动轨迹与CFD方法的略有差异。

图4 编程计算方法与CFD方法计算的颗粒运动状态

编程计算方法与CFD 方法计算的颗粒运动速度如图4（b）所示。从图中可见，与CFD 仿真分析方法相比，编程计算方法中颗粒刚从齿轮啮合处飞出时速度较小，其余时刻均较大，导致计算所得运动轨迹与CFD仿真分析方法的略有差异，其原因在于CFD方法考虑了连续相与离散相的耦合作用。与编程计算方法中的单向耦合相比，CFD方法计算的颗粒载荷略有差别，二者计算的运动轨迹误差约为5%，速度误差除刚开始时刻外其余约为3%，充分验证了VOF-DPM耦合模型的正确性，同时也证明了在本文颗粒质量轻、数量少的参数特点下，连续相与离散相的耦合作用对颗粒轨迹的影响较小，可以忽略。

2 附加力对金属屑运动的影响

颗粒在流场中除受到流体浮力、曳力、颗粒自身重力外，由于流体与颗粒的相对运动和流体自身的粘性，还受到其他的附加表面力作用。根据颗粒的承载类型，可将作用力分为如下类型：重力与浮力、气动阻力（流体曳力）、虚质量力、压力梯度力、热泳力、Brownian力、Saffman升力、Magnus升力等。

本章应用CFD 方法仿真计算颗粒在流场中的运动状态，并分析不同附加力对金属屑运动状态的影响。

2.1 虚质量力

颗粒周围流体加速运动时作用在颗粒上的附加力为虚质量力（Virtual Force）

式中：Cvm为虚质量系数，默认值为0.5。

从式（10）中可见，当流体的密度远小于颗粒的密度时，虚质量力数值会很小，例如本文中空气和颗粒的密度比仅为0.00014，但是油液与颗粒的密度比达到了0.11，此时虚质量力不可忽略，因此需要考虑虚质量力对颗粒轨迹的影响。

有/无附加虚质量力的颗粒运动轨迹对比如图5所示；主动齿轮分别旋转1、10、20、30、40、50 圈时，颗粒运动状态和油液体积分布如图6所示，其中左侧无附加力，右侧添加虚质量力，颗粒的运动位置见图中黄色方框处（下同）。

图5 有、无附加虚质量力的颗粒运动轨迹对比

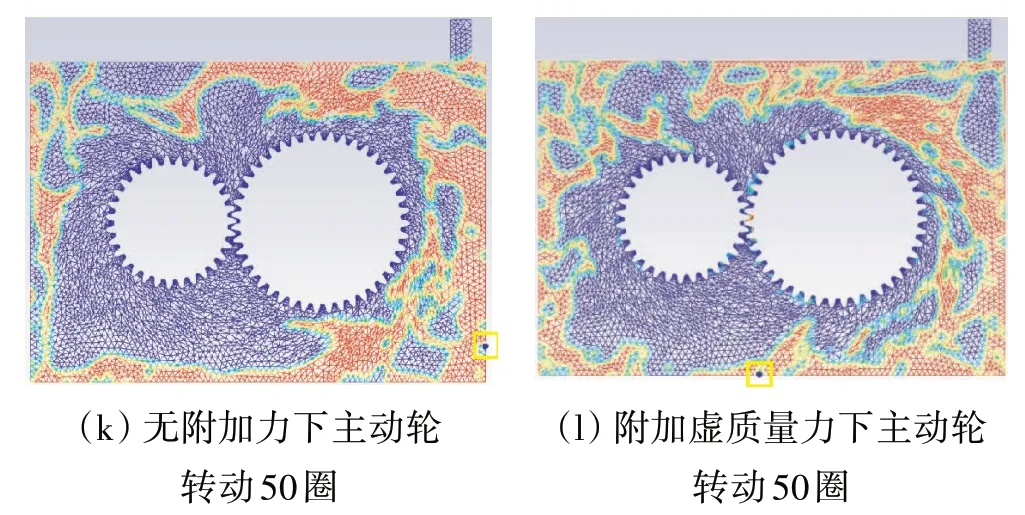
图6 有、无附加虚质量力的颗粒运动状态及油液分布对比

结合式（10）可见，当颗粒在空气中运动时，颗粒的密度远大于空气密度，此时空气对颗粒运动轨迹的影响很小，如图6（a）、（b）所示；但当颗粒进入油液之后，连续相流体的密度突变，此时连续相对颗粒附加的虚质量力不可忽略，从图6（c）、（d）中可见，主动轮转动10 圈后，颗粒已经脱离油液，且由于虚质量力的影响，颗粒脱离油液的射出角度不同，导致受到虚质量力的颗粒已经达到箱体的上半部分，撞击壁面反弹的入射角也不同，颗粒轨迹开始发生较大的变化，但运动趋势依旧是由齿轮的旋转和油液来主导，最终随着油液落至油池底部。

2.2 压力梯度力

流体的压力梯度作用在颗粒上的附加力为压力梯度力（Pressure Gradient Force）

压力梯度力与虚质量力相同，取决于连续相与离散相的密度比，因此同样需要考虑压力梯度力对颗粒运动轨迹的影响。

根据式（11），流体的密度对颗粒的压力梯度力有很大影响，有/无附加压力梯度力的颗粒运动轨迹对比如图7 所示，有/无附加压力梯度力的颗粒运动状态及油液分布对比如图8 所示。从图中可见，主动齿轮转动10 圈时，颗粒尚未摆脱油液，且在后续运动中始终处于油液当中；右侧添加压力梯度力相较于左侧无附加力的颗粒，齿轮转动50 圈内并没有围绕着齿轮运动，反而是受油液的压力梯度力影响一直位于箱体右半部分，可见油液中压力梯度力对颗粒运动状态影响极为明显。

图7 有、无附加压力梯度力的颗粒运动轨迹对比

图8 有、无附加压力梯度力的颗粒运动状态及油液分布对比

2.3 Saffman升力

颗粒在有速度梯度的流场中运动时，由于颗粒两侧的流速不一样，会产生一项由低速指向高速方向的升力，这就是Saffman升力

式中：K=2.594；dij为变形张量。

从式（12）中可见，Saffman 升力考虑的是剪切变形，这仅在小的颗粒雷诺数的流体运动中较为明显，因此Saffman 升力对亚微尺度的颗粒影响较大。有/无附加Saffman 升力的颗粒运动轨迹对比如图9 所示，有/无附加Saffman 升力的颗粒运动状态及油液分布对比如图10 所示。受到Saffman 升力的颗粒始终未能摆脱油液，除去左侧无附加力的颗粒撞击齿轮箱壁面反弹后的运动轨迹外，左右两侧有无Saffman升力的颗粒运动轨迹并无明显区别，因此在本文中可以选择忽略Saffman升力对颗粒运动轨迹的影响。

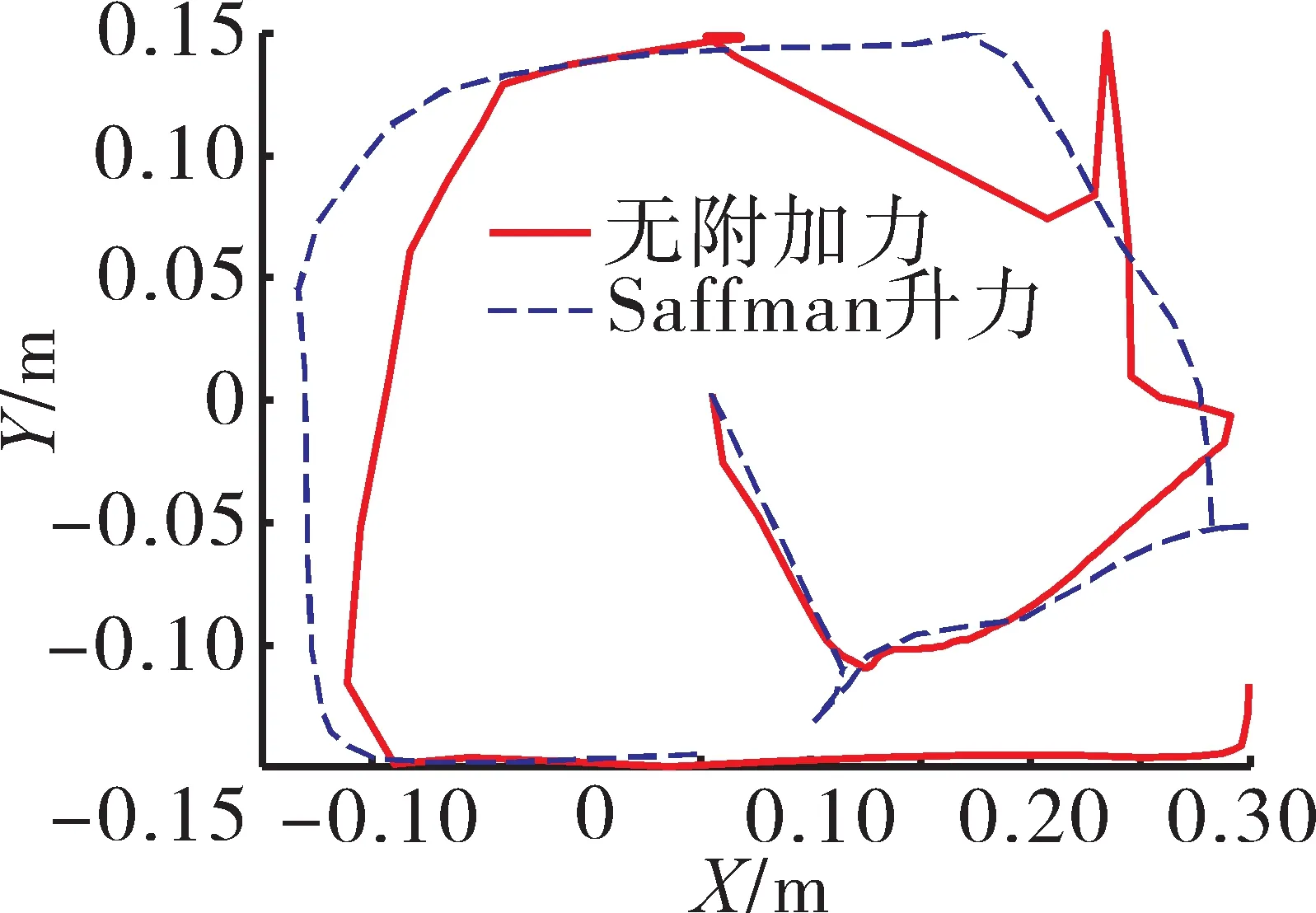
图9 有、无附加Saffman升力的颗粒运动轨迹对比

图10 有、无附加Saffman升力的颗粒运动状态及油液分布对比

2.4 Magnus升力

颗粒在流体中旋转时会产生Magnus 升力，这是由沿粒子表面的压力差引起的，高雷诺数情况下，Magnus升力FRL为

式中：Ap为颗粒投影面积，m2；V为流体-颗粒相对速度，m/s；Ω为流体-颗粒相对角速度，rad/s。

对于旋转升力系数CRL，常用以下2种计算方法。

（1）Oesterle and Bui Dinh[15]。旋转升力系数依赖于旋转雷诺数Reω与颗粒雷诺数Rep，该公式在Rep＜2000时与试验值吻合较好

（2）Tsuji et al[16]。旋转升力系数定义为自旋参数S的函数，该公式在Rep＜1600时广泛采用

自旋参数S定义为

有/无附加Magnus 升力的颗粒运动轨迹、运动状态及油液分布对比如图11、12 所示。从图中可见，在齿轮转动低于20 圈时，有/无附加Magnus 升力的颗粒运动轨迹较为接近，但当颗粒第1 次撞击到齿轮箱上壁面时（图12（c）），右侧受到Magnus 升力的颗粒被油液裹挟向后运动，由此开始二者的运动轨迹产生了较大的差异，因此Magnus升力对颗粒的运动影响不可忽略。

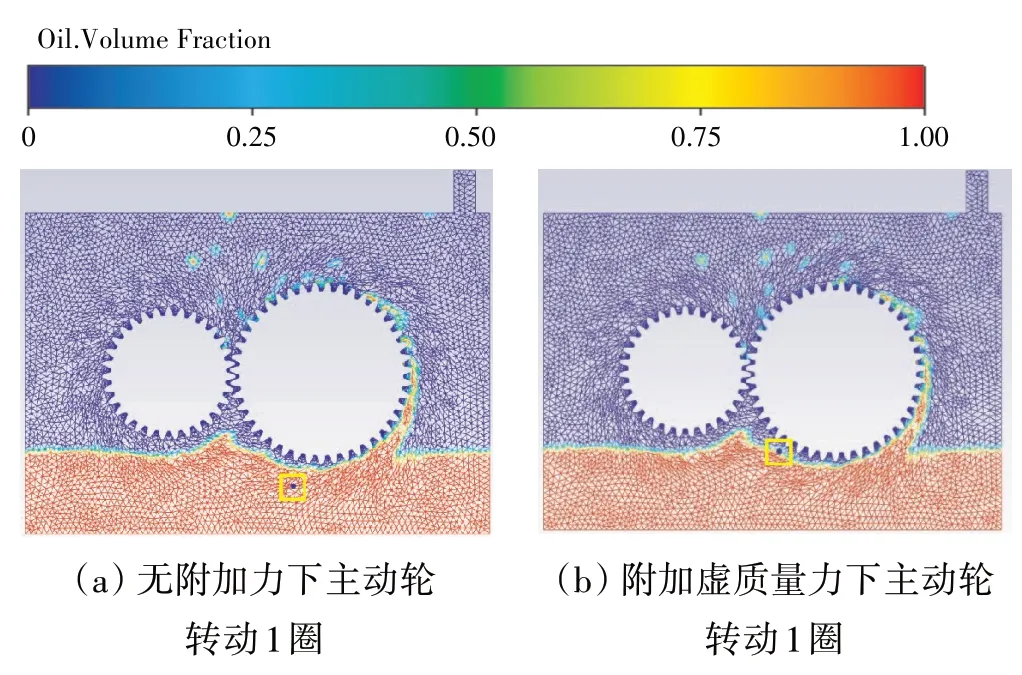
图11 有、无附加Magnus升力的颗粒运动轨迹对比

图12 有、无附加Magnus升力的颗粒运动状态及油液分布对比

2.5 热泳力

存在温度梯度的流体中悬浮的小颗粒受到的力与温度梯度方向相反，该现象称为热泳，可以在附加力中加入对粒子的热泳效应

式中：Dt，p为热泳系数，可定义为常数、多项式或用户自定义函数，也可采用Talbot[17]提出的形式

式中：Kn=2λ/dp，为Knudsen 数，λ为流体的平均自由程，m；K=k/kp，k为流体热导率，W/（m·K）；kp为颗粒热导率，W/（m·K）；Cs=1.17；Ct=2.18；T为流体温度，K；μ为流体粘度，Pa·s。

本文中减速器内部流场马赫数小于0.3，空气为不可压缩相，根据以往的研究成果，可不考虑温度变化和能量方程，因此忽略热泳力的影响。

2.6 Brownian力

对于亚微尺度的粒子，需要考虑布朗运动的影响。将布朗力的分量建模为谱强度为Sn，ij的高斯白噪声过程[18]

式中：δij为Kronecker δ函数，且有

式中：γ为流体的运动粘度，m2/s；Cc为Cunningham 修正系数；kB为Boltzmann 常数。布朗力分量的幅值定义为

式中：ξ为与单位方差无关的高斯随机数，均值为零。

每个时间步长计算布朗力分量的幅值，布朗力只适用于层流模拟。由于减速器内齿轮的旋转，箱体内时刻有湍涡流产生，不适用Brownian 力，因此可不考虑Brownian力对颗粒运动的影响。

3 结论

（1）采用编程计算与CFD 仿真对比的方式，验证了仿真模型的准确性。与单纯的连续相作用相比，连续相和离散相耦合作用对金属屑颗粒运动的影响较小，在2 种计算条件下的轨迹误差约5%、速度误差约3%，可忽略不计。

（2）基于CFD 方法对2 维减速器的仿真结果表明，虚质量力、压力梯度力和Magnus 升力对颗粒运动轨迹的影响较大；Saffman 升力对尺寸较大的颗粒运动轨迹影响较小，但对亚微尺寸颗粒运动有影响；热泳力与布朗力不适用于本文研究对象。在实际分析时应当结合实际情况施加相应的附加力。

（3）通过2 维减速器模型揭示了颗粒在减速器内部固、气、液多相耦合作用下的运动机理，可为预测减速器内部金属屑运动状态及运动轨迹提供技术方法。

（4）本文的研究方法方法可以拓展到3 维减速器仿真，以实现更准确的预测减速器内部金属屑运动状态，避免金属屑在减速器内部沉积，提升故障监控效果。