振动工况下特殊螺纹接头密封性能仿真研究
2023-09-14于洋屈展许富艳曹银萍窦益华刘渝
于洋 屈展,2 许富艳 曹银萍 窦益华 刘渝
(1.西北工业大学航空学院 2.西安石油大学石油工程学院 3.上海城建职业学院 4.西安石油大学机械工程学院)
0 引 言
大排量压裂及高产气作业过程中,因管内流体压力及流速的变化引起管柱振动,并在管柱上产生动态载荷[1-2]。特殊螺纹接头作为油管的连接结构,在复杂的载荷工况下常发生密封失效,甚至由此引发安全事故[3]。传统的研究多集中于静力学分析,考虑不同密封结构及载荷工况,分析特殊螺纹接头等效应力、接触压力及接触长度等对特殊螺纹接头密封性能的影响[4-6]。许红林等[7]基于赫兹接触理论,建立了球面对锥面密封形式的接触模型,计算了球面半径对接触压力和有效接触长度的影响。张颖等[8]建立了特殊螺纹接头泄漏模型,分析了密封面平均接触压力、密封面表面粗糙度及密封面有效长度对气体泄漏率的影响。窦益华等[9-10]基于有限元法,分别考虑不同密封结构、密封面参数及载荷工况,分析了特殊螺纹接头应力及接触压力分布对密封性能的影响。然而,以上基于静力学分析的方法无法有效解释因管柱振动引发特殊螺纹接头密封性能减弱的问题。特殊螺纹接头密封面可视为2个接触面,接触面主要承受法向载荷和切向载荷[11]。外压力的产生使接触面法向载荷改变,影响接触面的接触形貌及接触压力[12-13];切向载荷由管柱的轴向力产生,可引起密封面的水平滑移[14-15]。振动工况下,特殊螺纹接头密封面将发生微动,产生能量耗散,导致磨损或疲劳破坏[16]。张颖等[17]建立了密封面的接触压力模型,分析了振荡载荷下不同密封锥度对特殊螺纹接头能量耗散的影响。李凡等[18-19]将特殊螺纹接头密封面简化为剪切层微滑模型,基于能量耗散理论分析了动态载荷下接头的密封性能。上述研究为特殊螺纹接头密封性分析提供了新的思路,而建立的模型基于一定的简化和假设,并未考虑模态振型对密封性能的影响。
为此,本文基于能量耗散理论,考虑振动工况下密封面微观接触滑移的影响,建立了锥面-锥面特殊螺纹接头限元模型,通过振动模态分析,得到含特殊螺纹接头管柱的模态振型;通过摩擦接触分析,得到不同模态振型与上扣扭矩下接头的Von Mises应力、接触压力及摩擦力-位移迟滞曲线,据此研究特殊螺纹接头的密封性能,以期为特殊螺纹接头上扣扭矩控制及动载作用下密封性能评估提供参考。
1 模态振型的获取
为了获取振动工况下特殊螺纹接头的动态载荷,首先对含有接头的管柱进行模态分析。以线性模型为基础,管柱的振动方程为[20-21]:
(1)

无阻尼力的振动方程为:
(2)
若接头密封面在模态分析之前已有作用力(如上扣扭矩),则接触状态也会改变,刚度矩阵[K]随载荷的变化而变化。无阻尼力时式(1)可表示为:
(3)
式(3)中f(t)包含静态载荷f1(t)与动态载荷f2(t):
f(t)=f1(t)+f2(t)
(4)
动态载荷的幅值一般小于静态载荷的幅值,所以该幅值并不能打破由于静态载荷所建立的结构平衡状态。施加静态载荷后系统的刚度矩阵[K1(u)]为:
[K1(u)](u)=f1(t)
(5)
当f1(t)达到终值时,可以得到静态载荷作用后的终值(u)与[K1(u)]。此时的系统刚度矩阵[K1(u)]可以看作初始刚度矩阵。因此,方程(5)为:
(6)
计算特殊螺纹接头模态振型与模态频率分为2部分:第一部分是考虑接触条件下做一次静力学非线性分析,第二部分则是用传统模态分析求得结构的模态振型与模态频率。
2 特殊螺纹接头模态分析
基于以上模态分析理论,本文将模态振型的数据以循环位移的方式施加在含有特殊螺纹接头的油管上,通过提取密封面节点摩擦力与位移,求得各阶模态振型下特殊螺纹接头密封面的能量耗散。以ø88.9 mm×6.45 mm锥面-锥面特殊螺纹接头为研究对象(见图1),接头密封面锥度为1∶2,扭矩台肩角度为10°,螺纹牙承载面角度为-3°,螺纹牙导向面角度为10°,螺纹锥角为1∶16。

图1 锥面-锥面特殊螺纹接头结构示意图Fig.1 Schematic diagram for structure of cone-cone special threaded connector
建立含有特殊螺纹接头管柱的有限元模型,如图2所示,接头两端油管长度分别为9.8 m,并将接头以推荐的上扣扭矩拧紧,油管两端施加全约束。在上扣扭矩及外载作用下,由于特殊螺纹接头密封面和螺纹处发生弹、塑性变形,同时接触面将发生位移,需在ABAQUS软件中开启几何非线性和材料非线性[5]。相关材料参数如下:弹性模量210 GPa,泊松比0.3,摩擦因数0.1,最大屈服强度828 MPa,抗拉强度835 MPa。模型整体选用C3D8I单元,并分别对螺纹、密封面及扭矩台肩进行网格细化处理。为加快非线性分析的求解速度,同时保证计算的准确性,选用ABAQUS/Standard求解器进行求解分析。
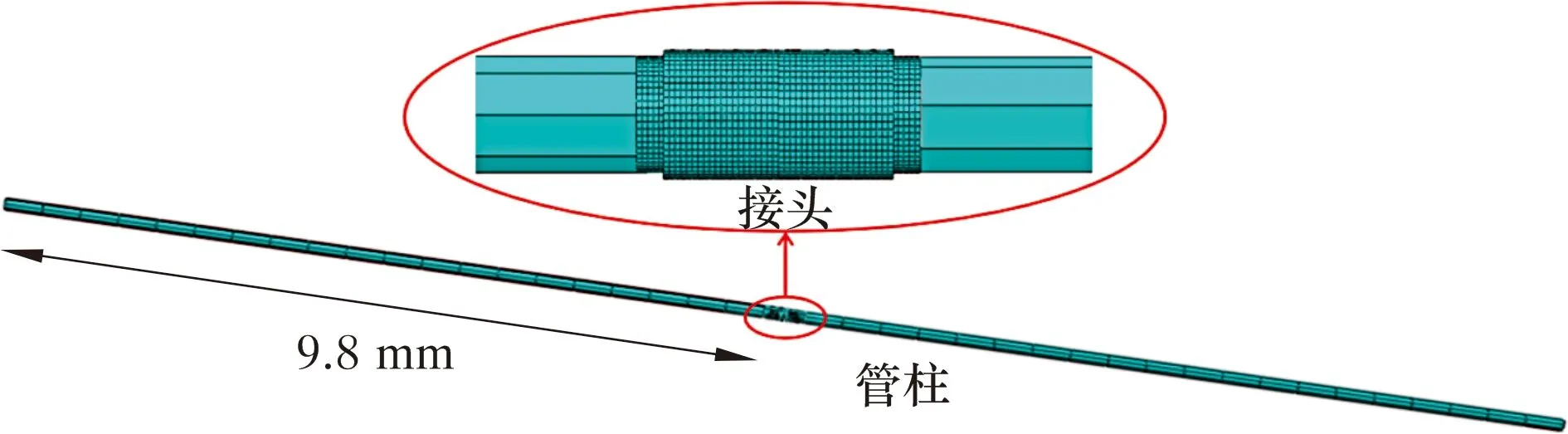
图2 含有特殊螺纹接头的管柱有限元模型Fig.2 Finite element model of pipe string with special threaded connector
在分析步程序类型中选择线性振动[22],采用频率的方式创建分析步,计算得到前4阶模态振型,如图3所示。由图3可知,1阶与2阶模态振型的最大位移在接头两端的油管中部,分别为0.021 4和0.021 7 mm;3阶与4阶模态振型的最大位移在接头部位,分别为0.055 41和0.055 45 mm,并发生了整体偏转。提取模态分析结果中的固有频率,前4阶的固有频率分别为1.23、1.28、3.58和3.58 Hz。
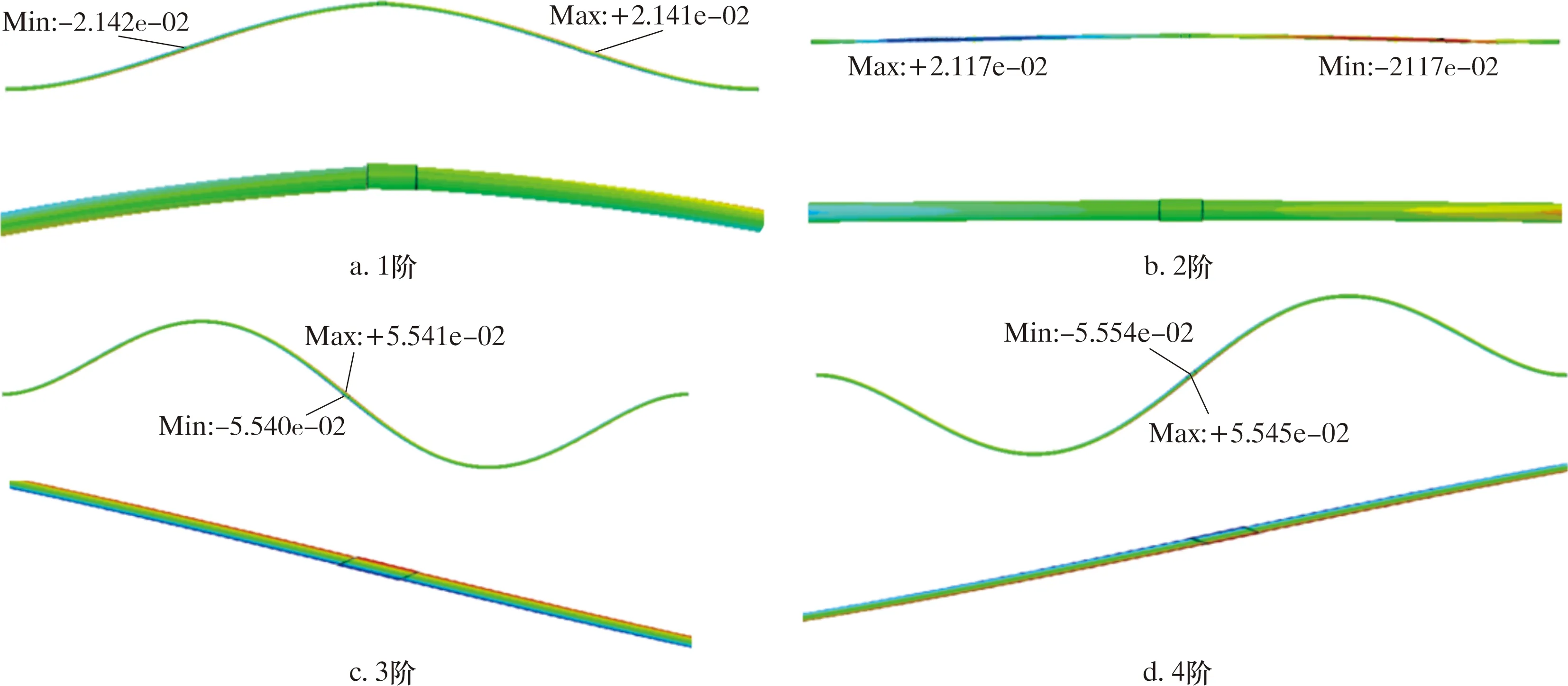
图3 管柱前4阶模态振型Fig.3 First four-order modal shapes of pipe string
3 接头应力与接触压力分析
由于管柱模型1阶与2阶、3阶与4阶的轴向位移幅值和固有频率几乎相同,故在以下分析中,将1阶与3阶的位移幅值作为交变位移载荷加载在管柱一端,另一端设置为全约束,然后进行模态振型下的非线性静力学分析。同时,由于上扣扭矩影响特殊螺纹接头的接触状态及能量耗散,所以考虑了最小、最佳及最大3种上扣扭矩的影响。
3.1 模态振型下特殊螺纹接头应力分析
不同模态振型与上扣扭矩下特殊螺纹接头密封面von Mises应力分布云图如图4所示。由图4可知,最大von Mises应力在密封面靠近扭矩台肩处,但均未超过材料的强度极限835 MPa;交变位移载荷加载完成后,1阶与3阶模态振型下,密封面最大von Mises应力变化较小,最大差值仅为3 MPa。相应随时间变化的密封面von Mises应力曲线如图5所示。
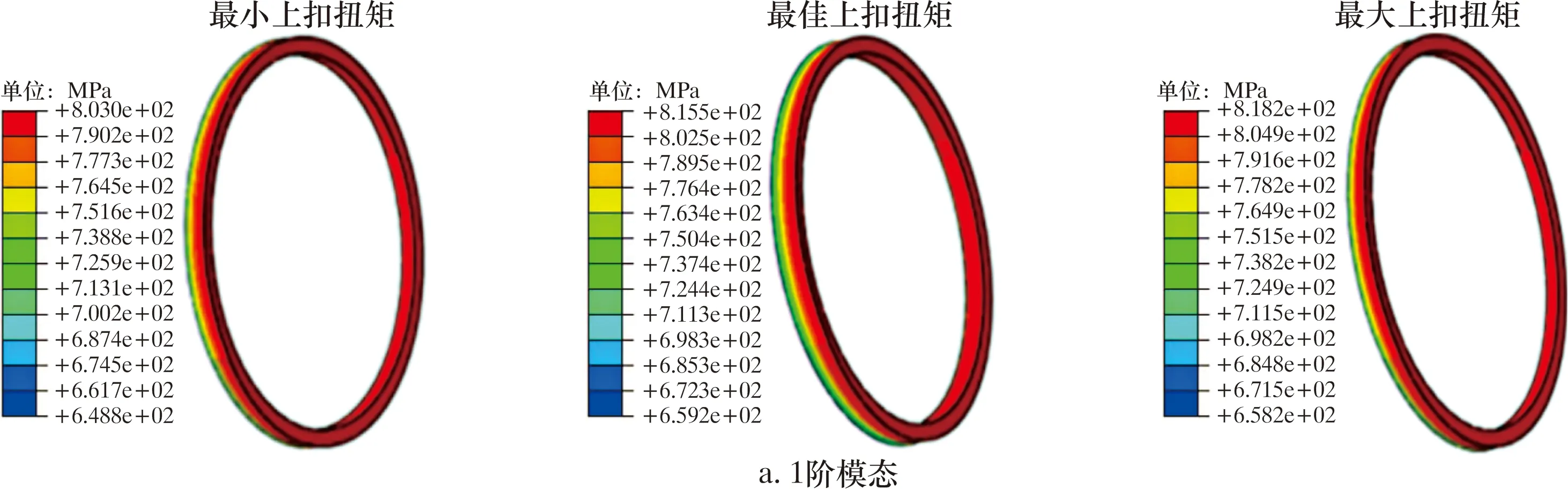
图4 不同模态振型与上扣扭矩下特殊螺纹接头密封面von Mises应力云图Fig.4 Cloud chart for von Mises stress of sealing surface of special threaded connector under different modal shapes and make-up torques

图5 不同模态振型与上扣扭矩下特殊螺纹接头密封面von Mises应力曲线Fig.5 Von Mises stress curve of sealing surface of special threaded connector under different modal shapes and make-up torques
图5中,0 s为上扣扭矩加载过程,0~0.4 s为轴向压缩位移加载与卸载过程,0.4~0.8 s为轴向拉伸位移加载与卸载过程。2种模态振型加载与卸载过程中,von Mises应力呈V形变化,没有应力显著增大的现象。仅在3阶模态振型下,当轴向拉伸位移达到峰值时,密封面von Mises应力最小。这是因为3阶模态振型的位移较大(约为1阶的2.6倍),使得密封面向油管端的滑移量增加,密封面的过盈量减小,从而导致von Mises应力减小。以上分析表明,1阶振型与3阶振型对特殊螺纹接头的应力影响较小。
3.2 模态振型下特殊螺纹接头接触压力分析
不同模态振型与上扣扭矩下特殊螺纹接头密封面接触压力分布如图6所示。由图6可知,交变位移载荷加载完成后,2种模态振型下最大接触压力同样位于密封面靠近扭矩台肩处,且密封面均保持了较高的接触压力。相应随时间变化的密封面接触压力曲线如图7所示。
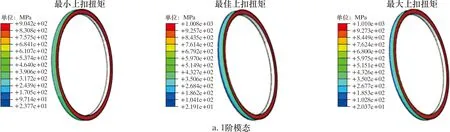
图6 不同模态振型与上扣扭矩下特殊螺纹接头密封面接触压力云图Fig.6 Cloud chart for contact pressure of sealing surface of special threaded connector under different modal shapes and make-up torques

图7 不同模态振型与上扣扭矩下特殊螺纹接头密封面接触压力曲线Fig.7 Contact pressure curve of sealing surface of special threaded connector under different modal shapes and make-up torques
由图7可以看出,1阶与3阶模态振型下,3种上扣扭矩的密封面接触压力随时间均呈正弦曲线规律变化,且3阶模态振型的变化幅值较大。虽然3阶模态振型下在加载轴向拉伸位移时,最小上扣扭矩的密封面接触压力的降幅最大,但仍保持了较高的接触压力(值为673 MPa)。在1个周期的交变位移载荷加载结束后,密封面的接触压力与初始值基本持平。
由以上分析可知,模态振型对特殊螺纹接头密封面von Mises应力及接触压力的影响并不明显,利用两者分析振动工况下接头密封性能具有一定的局限性。
4 接头能量耗散与密封性能分析
在外部递增载荷作用下,密封面首先发生微观滑移(黏着与滑移共存)。随着载荷进一步增大,密封面发生宏观滑移。在1个循环载荷作用周期内,各种滑移相互转换,出现力-位移迟滞现象,则力与位移迟滞曲线包含的面积即为1个周期内密封面产生的能量耗散[16]。
不同模态振型与上扣扭矩下密封面摩擦力、位移随时间变化曲线如图8所示。由图8可知:1阶模态振型下力、位移曲线重合度较高;3阶模态振型下密封面的力、位移分离度较大,表明后者的迟滞现象较明显。提取图8中密封面位移、摩擦力的幅值,如表1所示。

表1 不同模态振型与上扣扭矩下密封面摩擦力与位移幅值Table 1 Friction and displacement amplitude of sealing surface under different modal shapes and make-up torques
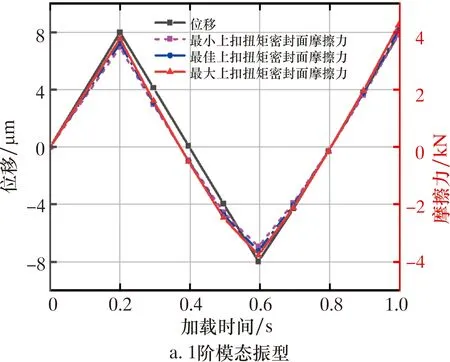
图8 不同模态振型与上扣扭矩下密封面摩擦力与位移随时间变化曲线Fig.8 Time dependent curves of friction and displacement of sealing surface under different modal shapes and make-up torques
由表1可以看出,模态振型下,特殊螺纹接头密封面的位移为微米级,且摩擦力随上扣扭矩的增大而增大。3阶模态振型下,密封面的滑移量和摩擦力的变化幅值分别为1阶模态振型的2.5和1.3倍。
不同模态振型与上扣扭矩下密封面摩擦力-位移迟滞曲线如图9所示。
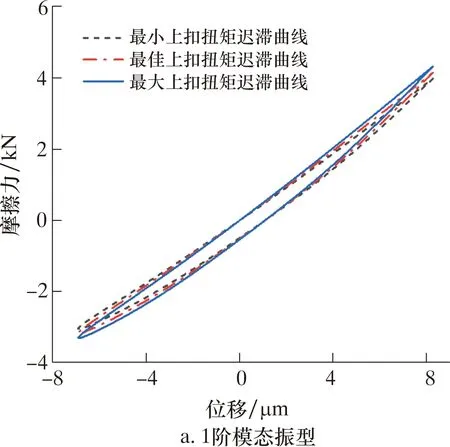
图9 不同模态振型与上扣扭矩下密封面摩擦力-位移迟滞曲线Fig.9 Friction-displacement lag curves of sealing surface under different modal shapes and make-up torques
由图9可知,2种模态振型下,密封面的迟滞曲线均呈“针叶”形,处于微观滑移状态,没有宏观滑移。由Mindlin理论可知,此时密封面的接触边缘发生微观滑移,而中心处于黏着状态[16]。相较于1阶模型振型,3阶模态振型下密封面黏着区域较小,微观滑移较大。通过计算迟滞曲线的面积,得到相应的能量耗散,如图10所示。由图10可知:3阶模态振型下密封面的能量耗散约为1阶模态的3.2倍;相同模态振型下,上扣扭矩越大,能量耗散越大。振动工况产生的能量耗散可以造成接触面摩擦磨损,也可加速疲劳裂纹的萌生[23],导致特殊螺纹接头密封性能减弱。在长期振动作用下,将导致接头密封失效或使用寿命缩短。因此,利用力-位移迟滞曲线分析密封面的接触滑移状态及能量耗散,可以明显反映出振动工况对特殊螺纹接头密封性能的影响。
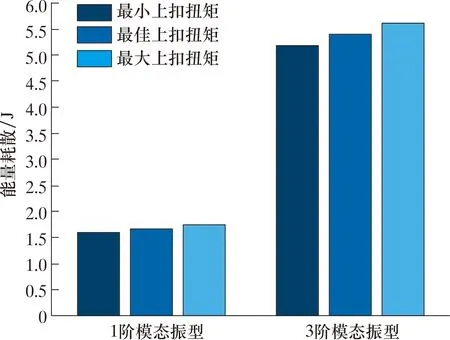
图10 不同模态振型与上扣扭矩下密封面能量耗散Fig.10 Energy dissipation of sealing surface under different modal shapes and make-up torques
以上研究表明,振动工况下特殊螺纹接头密封面的滑移量极小,可达到微米级,这对基于静力学分析接头von Mises应力及接触压力的影响并不明显,不能有效解释因振动引发特殊螺纹接头密封性能减弱的问题。而利用能量耗散理论从微观层面研究接头密封性能的方法,可以有效解决这一问题。
5 结 论
(1)模态振型对特殊螺纹接头密封面von Mises应力及接触压力的影响并不明显,而基于能量耗散理论,利用力-位移迟滞特性分析密封面的接触滑移状态及能量耗散,可从微观层面解释因管柱振动引发特殊螺纹接头密封性能减弱的问题。
(2)模态振型下,特殊螺纹接头密封面间的摩擦力与能量耗散均随上扣扭矩的增大而增大;3阶模态振型下,密封面的摩擦力、位移迟滞现象明显,其能量耗散值大于1阶模态。
(3)模态振型下,特殊螺纹接头密封面的位移为微米级,密封面的摩擦力-位移迟滞曲线呈“针叶”形,处于黏着与滑移共存的微观滑移状态。长期振动工况下,易造成密封面磨损,导致特殊螺纹接头密封性能减弱甚至密封失效。
