基于响应面法的压裂液混砂搅拌系统结构优化
2023-09-14刘子豪朱青林管锋万锋刘先明李梓睿
刘子豪 朱青林 管锋 万锋 刘先明 李梓睿
(长江大学机械工程学院)
0 引 言
携砂液质量与搅拌装置的混合特性之间存在着紧密的联系,因此,配制不同压裂工艺要求的携砂液是压裂混砂搅拌系统的主要作用。在实际压裂作业过程中,经常会出现携砂液混合不均匀、质量不达标等问题,严重影响压裂作业效果[1]。
混砂车搅拌装置中重要的工作部件——搅拌器,对搅拌效果起着决定性的作用。但目前混砂车搅拌装置的流体混合效率仍然偏低,造成其搅拌功率普遍偏高。因此需设计具有良好混合性能的压裂液搅拌装置。姜小放等[2]、秦斌[3]利用Fluent软件对搅拌罐流场的影响因素进行了模拟,发现设置挡板可以增强流场的湍流能力,提出挡板的高度、宽度、形状可以在实际应用中进行调整,从而提高生产效率。宋康康等[4]、黄天成等[5]、李龙杰[6]、S.S.HOSSEINI等[7]为提高压裂混砂搅拌装置的搅拌效果,以混砂搅拌装置的搅拌时间作为评价指标,并针对搅拌叶轮的结构特点,对压裂混砂搅拌装置的搅拌效果进行了评价;采用正交试验和CFD数值模拟相结合的方法,研究了混合叶轮的主要几何尺寸对混合时间的影响规律。殷瑱等[8]利用正交软件对不同结构参数下的搅拌功率进行分析,基于Fluent数值模拟分析压裂液搅拌装置功率,从而得到影响搅拌功率的最优组合。黄天成等[9]针对压裂搅拌的特点和对压裂混合液的质量要求,确定了压裂混砂设备关键部件搅拌叶轮和混砂罐的结构设计方法。
但上述方法无法构建各结构参数与优化目标之间的数学模型,只能在试验组所涉及的因素水平范围内进行参数优选,并没有综合考虑其他结构参数导致搅拌效果不佳的问题。
为此,笔者基于响应面优化方法,对混砂搅拌系统结构参数进行了优化,并建立了可预测结构参数与混砂搅拌混合时间的数学模型,验证了模型预测和优化结果的准确性,实现了理论上指导压裂混砂搅拌系统的设计。而且为了使仿真结果与现场实际更为贴合,构建了幂律型非牛顿流体混砂搅拌罐有限元模型,以此减小仿真结果与实际结果间的差异。研究结果可为压裂液混砂搅拌系统的优化提供参考。
1 结构及工作原理
机械搅拌设备在工艺过程中具有重要作用,可以用于混合、传质和传热。本文介绍的压裂液混砂搅拌系统采用了桨式搅拌器。桨式搅拌器有2种形式,一种是平浆式,一种是斜浆式。平桨式搅拌器由直径与高度之比为 4~10、圆周速度为1.53 m/s的2片平直桨叶组成,其所产生的径向液流速度较小。在平直桨叶低速转动时,液体主要为水平环向流动;在桨叶转动速度增加的情况下,液体的主要流向由水平环向流变为径向流动。因此平直桨叶的桨式搅拌器属于径流式搅拌器。斜桨式搅拌器的叶片相反折转45°或60°,其叶面与旋转方向成一定的倾斜角。当桨叶低速旋转时,液体既有水平环向流动,又有轴向的分流;当桨叶转速增高时,液体还有较大的径向流。因此,斜桨叶搅拌器介于径流型和轴流型搅拌器之间,但更接近于轴流型搅拌器。上述2种形式的搅拌器在中央安装和较高的转速下,中心区域的上层液体会产生凹陷的涡漩,一般称为圆柱状回转区,在这个涡漩中的液体随着搅拌器一起转动,无法起到搅动作用,形成一个搅动死区。将一定数量的立式挡板或导流筒安装在搅拌容器中,可以消除此类漩涡[10]。
本文研究的是一种新型混砂车搅拌罐(见图1),采用内置扰流板的立式罐,底部采用平面底板。整个罐体分内外2层,基液从外罐体中部沿切向进入,经环形腔体循环后由内罐体弯管进入搅拌区,经与罐顶加入的石英砂充分混合后通过排出口排出。搅拌罐外层罐体直径D1=1 984 mm,内层罐体直径D2=1 784 mm,罐体高H=745 mm,采用双层桨式结构。这种搅拌罐的初始结构参数根据实验室前期通过正交试验法优选后的结果确定,并通过正交试验因素分析选定了4个主要影响因素:下搅拌叶角度(A)、下搅拌叶直径(B)、扰流板角度(C)和扰流板数量(D)。主要结构参数初始尺寸为:下搅拌叶角度67.5°,下搅拌叶直径1 230 mm,扰流板角度45°,扰流板数量6个。以上述4个结构参数为输入自变量,以搅拌的混合时间为因变量,构建混砂搅拌罐的结构参数与混合时间的数学模型,进而确定出最佳的多参数优化匹配方案。
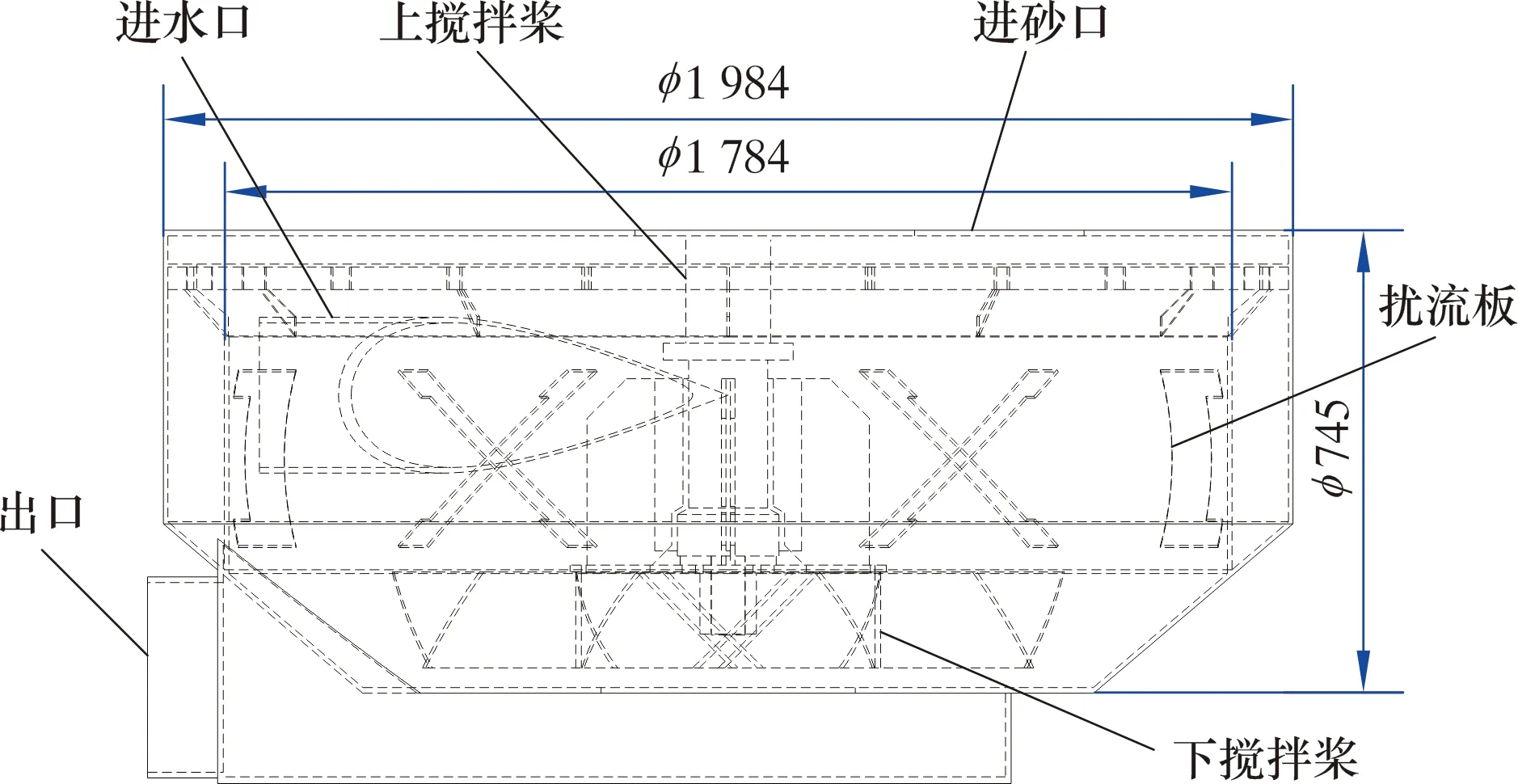
图1 混砂罐几何模型Fig.1 Geometric model of sand mixing tank
2 有限元模型建立
2.1 流体力学模型
在混砂罐中进行搅拌时,可以把搅拌流场看作是固液的两相流动。在这个过程中,固体颗粒会随着液体的随机运动而移动。这一过程受到颗粒沉降速度、局部流体速度和湍流强度的影响。本文假设两相分别遵循各自的控制方程,并且流体是等温的,这不会影响模拟结果。由于压裂液中砂粒颗粒体积分数较高,占据总体积的15%,所以不能被忽略。为了分析这种情况,本文使用了欧拉多相流模型中的Euler模型。在这个模型中,流体与砂粒被认为是共同存在相互渗透的连续介质,通过质量守恒方程和动量守恒方程得到液体和砂粒之间的耦合(complex)[11]。
质量守恒方程为:

(1)

(2)
动量守恒方程为:


(3)


(4)
式中:α为体积分数;ρ为密度,kg/m3;v为速度,m/s;τ为应力张量,N/m2;p为固液两相共同承受的压力,Pa;ps为固相额外承受的压力,Pa;Kls为固液两相动量交换系数,kg/(m3·s);g为重力加速度,m/s2;下标l、s分别表示液相和固相。
在考虑两相(液相和固相)间动量和能量交换的问题时,用欧拉模型计算,其前提是假定没有质量传递,只通过动量和能量交换。液相和固相的相互作用是通过能量交换项和连续相作用在分散相上的曳力实现。在Wen-Yu模型[12]中,使用动量交换系数Kls来衡量相间的动量交换,以实现两相间的相互作用:
(5)
(6)
(7)
式中:CD为曳力系数;Res为颗粒雷诺数;ds为固相颗粒直径,m;μ1为液相黏度,Pa· s。
2.2 参数设置及边界条件
本文使用 Mesh进行网格划分。在混砂罐搅拌区中选取流体作为计算域,将整个搅拌罐流体域分为旋转域和外流域2部分。下叶轮区域为动区域(旋转域),其他部分为静止区域(外流域);动区域采用滑移网格设置,动区域与静区域通过交界面来传递数据,如图2所示。由于混砂车搅拌罐的几何结构复杂,故采用非结构化网格划分方法对流体域进行网格划分,并且为了提高计算精度,对上、下2桨叶区的网格进行了加密处理。验证发现,当网格数大于1 100 000时,搅拌罐内同一点同一时间混合时间变化小于5%。因此本文对于每个模型的网格划分都保持在1 200 000个单元左右。
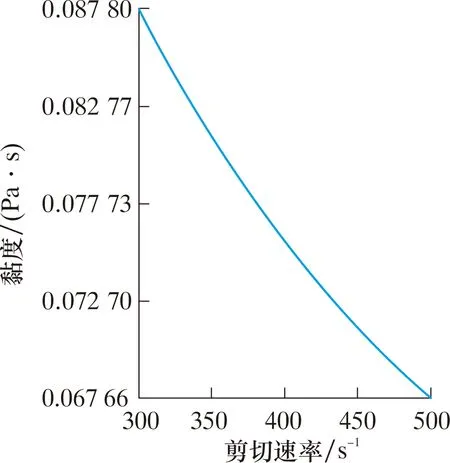
图3 幂律型介质流变曲线Fig.3 Rheological curve of power law type medium
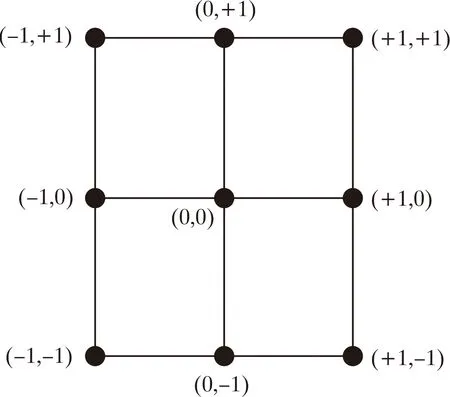
图4 Box-Behnken设计试验点分布Fig.4 Distribution of Box-Behnken design test points
采用欧拉多相流模型进行两相间模拟计算,湍流模型选择标准k-ε模型。混砂车搅拌罐的轴转速100 r/min。压裂液设定为幂律型非牛顿流体,其流变参数为:稠度系数K=1.61 Pa·sn,幂律指数n= 0.49,钻井液密度1 200 kg/m3[13],幂律流变曲线如图 3 所示。固相为砂粒,黏度0.01 Pa·s,密度为 1 500 kg/m3。设定以速度入口为入口边界,压力出口为出口边界,标准大气压为出口压力,壁面上以壁面函数法处理并采用无滑移的边界条件。混砂车搅拌罐内的搅拌过程按照上述初始结构参数和操作条件进行模拟。由于在湍流模式下,Fluent软件并没有提供相应的幂律流变模型。因此,用户需要使用UDF编程来确定幂律流体的本构方程。本文采用C++语言编写了幂律型非牛顿流体,并使用DEFINE宏来定义。UDF中可以使用Fluent提供的预定义宏,通过这些预定义宏,可以获取Fluent求解器得到的数据。最终,定义了混合时间的概念,即在试验中,出口监测点砂相达到最终平均体积分数(偏差在5%以内)的流场体积达到一定体积分数(15%)所需的时间[14]。
3 结果分析
3.1 BBD试验设计及方程构建
响应面设计是一种常见的试验设计方法,采用3个水平(中心点 0,低水平点-1,高水平点+1)的试验点,结合因素设计和不完全集合区设计,具体分布可参考图 4。通过寻找回归方程的最优参数组合,可以研究因素和响应之间的关系。响应面设计的优点在于可以估算出1阶、2阶及交互作用项的系数,使之成为测试次数较少的高效设计方式。因此,本文采用了BBD试验设计方法来确定混砂搅拌罐混合时间的试验方案。具体的因素水平及编码值见表1。
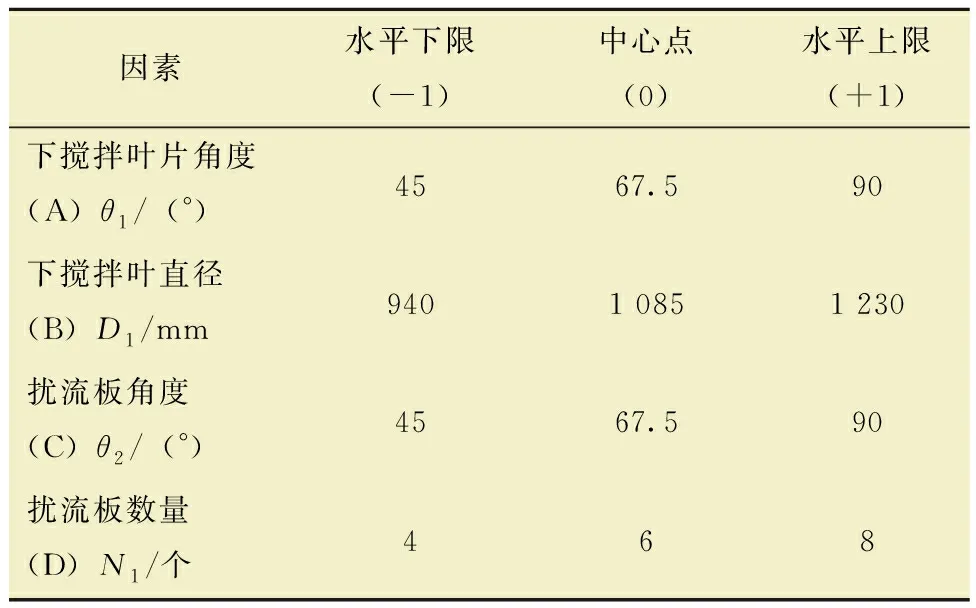
表1 结构因素及其水平Table 1 Structural factors and their levels
本文通过对表1中不同结构参数因素水平进行设计,生成了29组BBD试验方案,并针对不同试验组中的结构参数建立了混砂搅拌罐流体域模型。对这些模型进行相同水平的网格划分并进行数值模拟分析,收集不同试验组的仿真结果数据,最终得出BBD试验设计方案及数值模拟结果,结果汇总见表2。

表2 BBD设计及试验结果Table 2 BBD design and test results
笔者利用2阶模型对表2中的数据进行了二次多项式拟合,并通过多元线性回归分析得出了结构参数与混砂搅拌罐混合时间y之间的回归方程,具体表达如下:
y=692.902 1-0.374 52A-1.008 2B-0.995 47C+
3.079 89D-3.065 13×10-5AB+2.469 14×10-4AC-
0.051 111AD+4.061 3×10-4BC+1.120 69×10-3BD-
0.028 333CD+7.794 24×10-3A2+3.820 85×10-4B2+4.584 36×10-3C2+0.020 833D2
(8)
3.2 方差分析
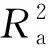

表3 回归方程的方差分析结果Table 3 Variance analysis results of regression equation

表4 回归模型误差统计分析结果Table 4 Statistical analysis results of regression model errors
3.3 预测准确性验证
为了验证下搅拌叶角度(A)、下搅拌叶直径(B)、扰流板角度(C)及扰流板数量(D)这4个结构参数在表1所示范围内变化时,反映结构参数与混合时间的预测模型(式(8))的预测结果准确性,根据预测的最优4个结构参数数值建模,采用与BBD试验相同的数值模拟方法开展数值模拟分析,结果如表5所示。由表5可以看出,预测值与试验值的相对误差为6.43%,从而验证模型预测结果的准确性。

表5 模型精度验证对比Table 5 Accuracy verification comparison of model
3.4 优化有效性验证
通过最小二乘法对构建的结构参数与混合时间的回归方程进行偏微分求导,计算得出可使混合时间取极小值的结构参数匹配方案即为响应面优化后的最佳设计点。考虑到加工等问题,将部分参数进行圆整计算,得到优化后的结构参数为:下搅拌叶角度(A)46.77°,下搅拌叶直径(B)1 230 mm,扰流板角度(C)65.87°,扰流板数量(D)5个。优化后的结构参数如表6所示。图5所示为优化前后砂相体积分数随时间的变化曲线。由图5可知,优化后的混砂搅拌罐出口砂相混合均匀的时间明显缩短,说明优化后的结构能提高搅拌效果,有更好的搅拌特性。数值模拟结果显示,优化前混合时间为32.7 s,优化后混合时间为18.9 s,混合时间明显缩短,充分验证了响应面优化结果的精确性和高效性。
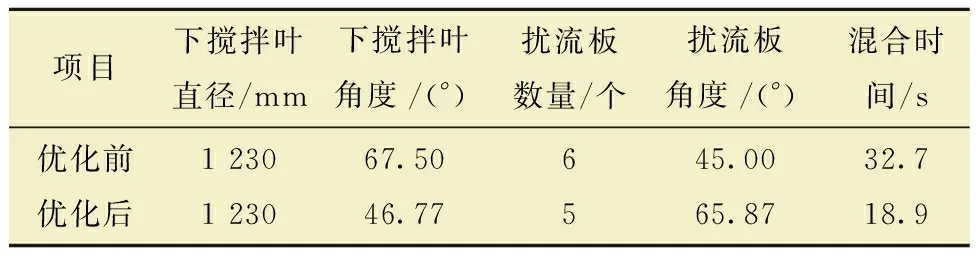
表6 模型优化有效性对比Table 6 Comparison of model optimization effectiveness

图5 砂相体积分数变化曲线Fig.5 Volume fraction variation curve of sand facies
4 结 论
(1)采用BBD试验设计方法构建结构参数与混砂搅拌罐混合时间的数学模型具有可行性。由此方法得到了基于2阶多项式构建的混砂搅拌罐混合时间预测模型。
(2)通过开展预测准确性验证,验证了构建的数学模型可以对参数水平范围内的混合时间进行准确预测,混合时间的模型预测值与实际值的相对误差为6.43%。
(3)基于幂律型非牛顿流体压裂液构建的混砂搅拌罐混合时间预测模型得到的优化结构参数,可以有效提高混砂搅拌系统的混合效果,优化后结构的混合时间为18.9 s,比结构优化前的32.7 s明显缩短,表明该结构优化的有效性和可行性。
