声学和电流特征融合的行星齿轮箱诊断方法
2023-09-14张娜段礼祥李肇阳樊晓萱
张娜 段礼祥 李肇阳 樊晓萱
(中国石油大学(北京)安全与海洋工程学院;应急管理部油气生产安全与应急技术重点实验室)
0 引 言
行星齿轮箱因传动比大、承载能力强的优点在页岩气压裂作业[1-2]、海上风电等油气行业的大型装备中发挥了关键作用。例如在压裂泵机组中,行星齿轮箱一端连接压裂泵动力端,另一端连接电机,实现动力传递和调速[3]。一旦行星齿轮箱发生故障,将影响正常的运转,可能导致压裂泵转速骤变,甚至停机。而大型机组若因故停机,不仅再启动时耗时长,还会导致下一级装置停车、可靠性降低和进一步的危害。因此,关注行星齿轮箱的安全性并进行故障诊断具有重要意义。
目前行星齿轮箱故障诊断多依靠振动传感器实现[4-7],主要因为采集所得的振动信号受外界干扰较小且稳定性较强。但是振动传感器作为接触式传感器不仅需要与设备直接接触,而且需慎重确定安装位置,因为安装位置直接影响采集到的信号中含有故障信息的量[8]。然而,在压裂作业等现场可能存在机组行星齿轮箱处表面温度过高、理想安装位置不允许改造(如打磨、钻孔)等难题,限制了接触传感器的安装。为此,研究人员通过非接触传感器实现行星齿轮箱故障诊断。付国梓等[9]依靠声学传感器,通过改进多尺度熵和支持向量机结合实现行星齿轮箱故障诊断;JIANG Z.K.等[10]提出依靠电流传感器的行星齿轮箱故障诊断方法。但以上依靠单一非接触传感器的行星齿轮箱诊断方法,不仅需要进行复杂度高的信号处理,而且诊断效果不够理想。
原因之一是行星齿轮箱特殊的运动形式使得传感器获取的是经过复杂传输路径衰减后的信号,所以其故障特征微弱[11]。而且声学传感器易受环境噪声干扰,使得声学信号信噪比低,加剧了故障特征的提取难度[12];电流传感器无法像振动、声学传感器那样通过尽量靠近故障发生位置增强故障特征,加之电流工频的突出,导致电机电流信号中故障特征不明显[13]。此外,不同传感器对各故障敏感度不同,使得单一信号获取的特征信息不完备[14],难以准确表征行星齿轮箱状态。以上原因均可使故障诊断效果差。
多传感器融合能充分利用信号间的互补来丰富特征信息[15],提高故障识别的准确性。例如段礼祥等[14]通过融合振动信号和红外图像获取了旋转机械故障的互补特征信息,实现了精确诊断;武国营等[16]融合温度和压力传感器信息,大幅提高了液压动力单元失效诊断准确性。在行星齿轮箱故障诊断领域也有研究人员采用多传感器融合,例如:李峰[17]提出一种电机电流信号和振动信号融合的行星齿轮箱故障诊断方法;JING L.Y.等[18]提出一种融合声学、振动、瞬时角速度等信号的方法识别行星齿轮箱故障;魏秀业等[19]提出一种基于深度残差网络的行星齿轮箱故障多振动传感器特征融合诊断方法。
以上方法通过融合多个传感器,有效提升了故障诊断准确性。但目前基于多传感器融合的行星齿轮箱故障诊断研究主要是接触传感器与非接触传感器的融合,或多个接触传感器的融合,其中均含接触传感导致不适用于之前所提的限制情况;而且为了能从结构复杂的行星齿轮箱监测信号中提取到可靠特征,实现高效融合诊断,主要采用结构较深的网络,如InceptionNet[20-21]、ResNet[22-23]、DenseNet[24]等,导致存在参数量大、复杂度高、计算效率低的问题。
针对以上问题,笔者研究了一种从2个非接触传感器(即声学和电流传感器)信号中提取和融合特征的方法。该方法首先通过经验模态分解与快速傅里叶变换对电机电流信号进行预处理,将声学信号和预处理后电机电流信号作为网络的输入。然后设计了一个轻量化的多尺度解耦卷积网络,该网络主要采用多尺度的解耦卷积、串行并行计算和金字塔池化模块对标准卷积网络进行改进。其中多尺度的解耦卷积用以提取信号中微弱、对类间差异敏感的特征,增大感受野,进而加快网络收敛、轻量化网络结构;串行、并行计算实现特征融合,增强特征完备性;金字塔池化模块用以减少特征丢失。笔者还开展了行星齿轮箱典型故障模拟试验,采集了声学信号和电机电流信号,对所提方法的有效性进行验证。研究结果可为行星齿轮箱的故障诊断提供参考。
1 理论分析
1.1 解耦卷积
标准卷积f(w,x)是权重w与输入x的内积,是通过计算内积衡量输入数据间的相似程度,其将类内变异和类间差异耦合在一个度量中。 具体可表示为:
f(w,x)=
(1)
标准卷积存在类内变异和类间差异难区分的问题。如当2个数据的内积相近时,存在2种可能:可能一为2个数据属于同一类状态;可能二为不属于一类状态但恰好内积相近,难以区分以致误诊断。
由于内积在数学中可进行分解:
(2)

fd(w,x)一般表示形式为:
(3)
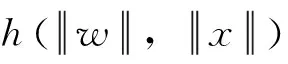
由式(3)可看出,其包含了标准卷积作为它的一种特殊情况。
文献[25]根据解耦卷积一般表示形式,提出了双曲正切卷积(Hyperbolic Tangent Convolution,TanhConv),具体计算为:
(4)
式中:m为控制输出范围;ρ为控制x的范数。
双曲正切卷积中幅值函数是一个有输出范围限制的常数,范围为[-m,m],表示双曲正切卷积考虑了类内变异,但有上界限制,卷积的结果将主要由角度函数决定,所以对类间差异更敏感。因此相比标准卷积,双曲正切卷积更能提取到信号中对类间差异敏感的特征,加速网络收敛。由于以上优点,采用解耦卷积能避免需多层标准卷积堆叠才能获取具有区分度的特征的情况,从而轻量化网络结构,提高计算效率。
1.2 多传感器深度特征融合
多传感器深度特征融合是指将多个传感器信号输入到深度学习网络中实现特征提取和融合[26]。采用较多的是卷积网络,其本身是一个融合结构,它能通过卷积、池化以及串行、并行计算等将特征提取、特征融合、分类集于一体[18]。其中串行、并行计算定义如下。
假设A、B为信息空间I相应的2个特征空间,对于任意信息样本ζ∈I,其对应的2个特征向量分别为α∈A和β∈B,γ为融合后的特征,于是串行计算为:
(5)
并行计算为:
(6)
1.3 金字塔池化模块
金字塔池化模块(Pyramid Pool Module,PPM)在2017年被提出[27],模块包括多阶池化、1×1卷积和上采样。
多阶池化由一组池化核大小不同的池化层组成,它将输入特征划分为多个子区域并各自作池化,获取含不同子区域间细节的特征。后经过1×1卷积使特征降维。再通过双线性插值对降维后特征上采样,使特征的尺寸与输入特征一致。最后通过串行计算实现多阶特征与输入特征的融合,减少特征信息丢失。
原始金字塔池化模块是对尺寸为(n,n)的输入特征提出的,但本文输入特征宽度固定为1,即输入特征尺寸为(1,li),其中li为特征长度。在本文中,假设划分为N个子区域作池化时,则池化核与步长的尺寸相等,具体尺寸计算为:

(7)
式中:Kpool为池化核;Spool为池化步长;⎣•,•」为向下取整符号。
2 声学和电机电流信号深度特征融合方法
2.1 声学信号
行星齿轮箱局部故障时,声学信号上会出现周期性冲击。虽然声学信号受噪声干扰大、信噪比低,使冲击不够突出,但故障状态与正常状态间仍然具有一定的可分性。
以行星齿轮箱中行星轮缺齿故障为例进行分析。图1为正常状态声学信号时域图。图2为行星轮缺齿状态声学信号时域图。
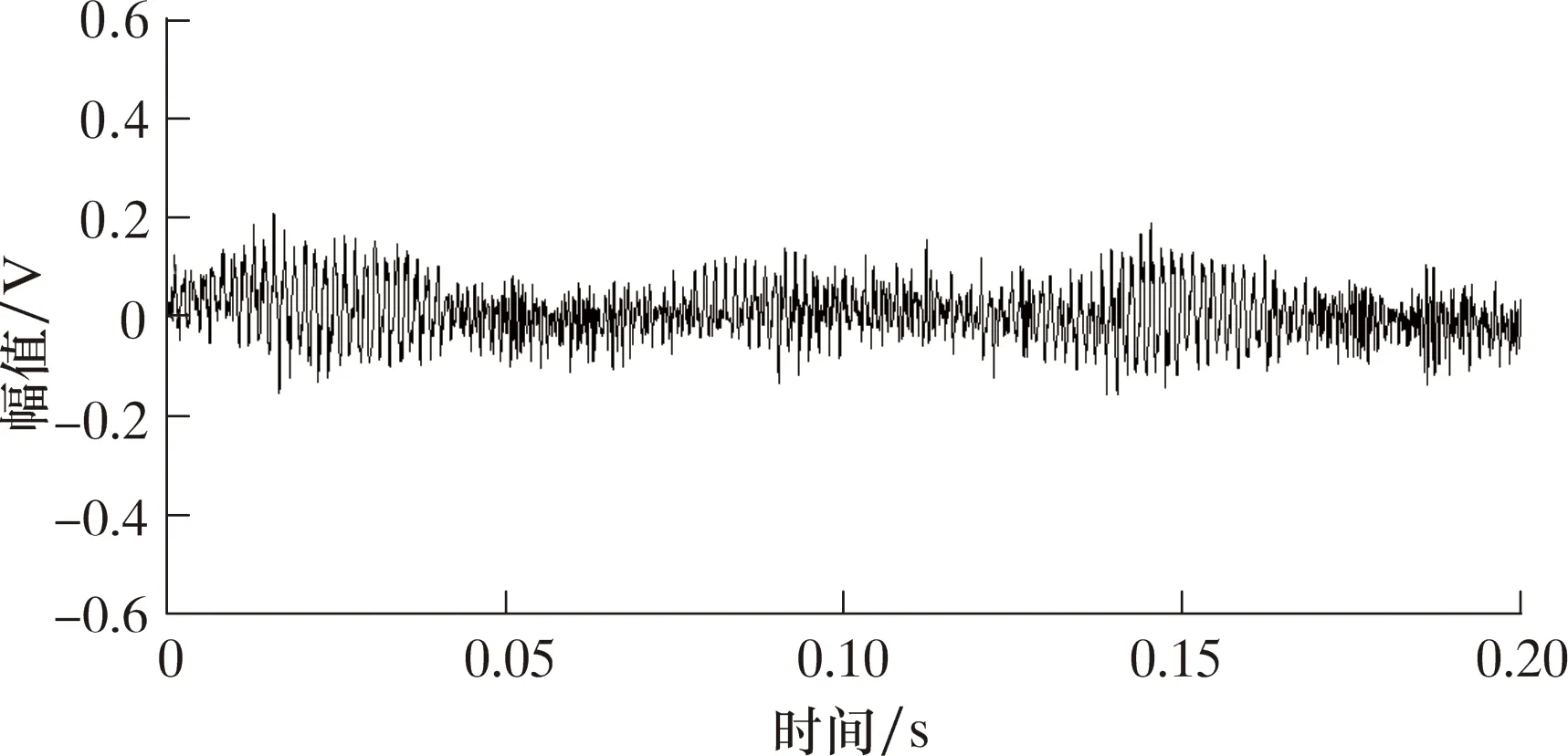
图1 正常状态声学信号时域图Fig.1 Time domain diagram of acoustic signal in normal state
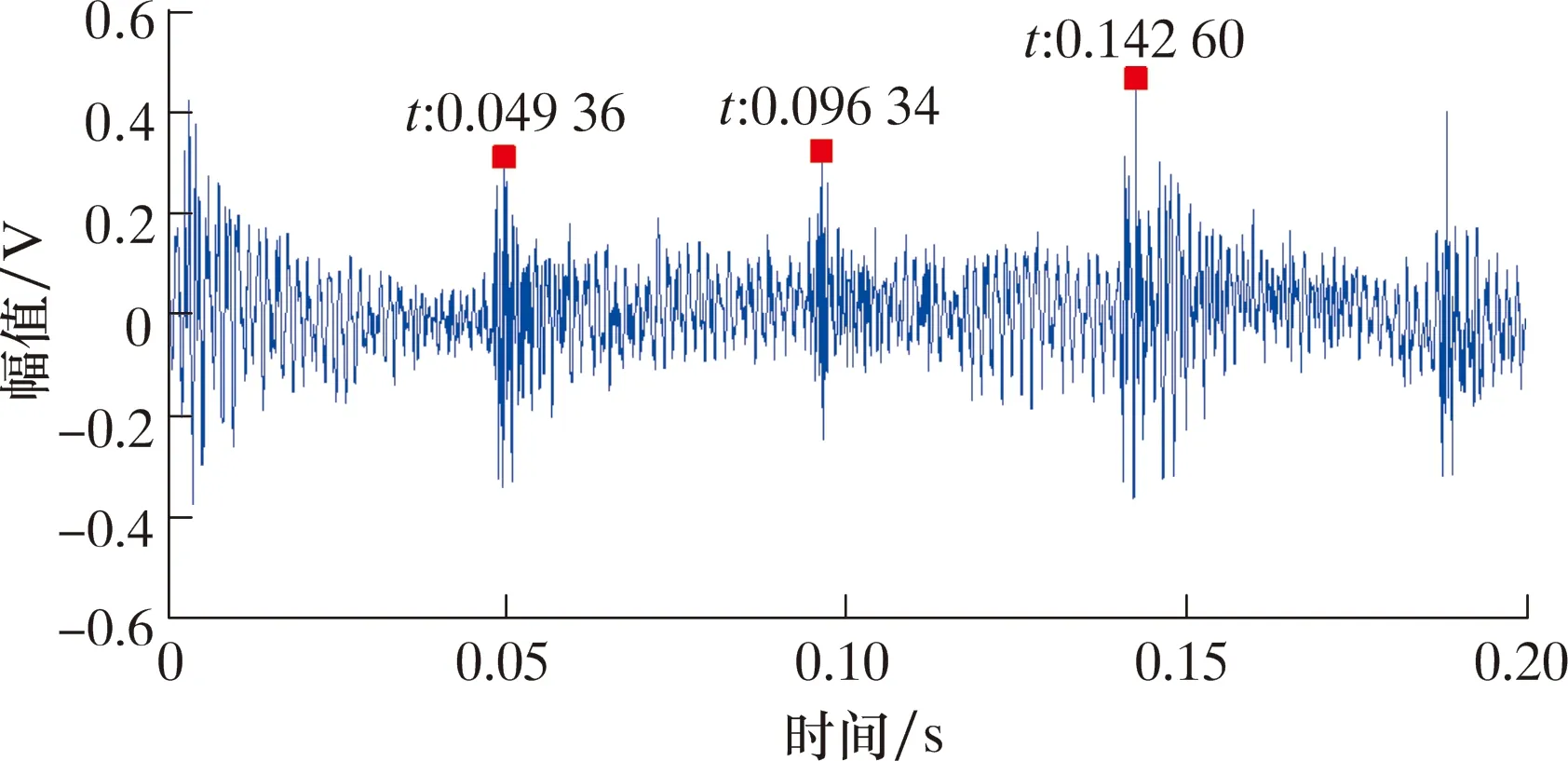
图2 行星轮缺齿状态声学信号时域图Fig.2 Time domain diagram of acoustic signal in epicyclic gear teeth missing state
对比可知,缺齿状态信号中含周期性冲击,其周期为1/frps(frp为行星轮转频),且与正常状态间存在稳定的差异,可以相互区分。为了能定量地说明存在差异,采用对冲击敏感的峭度指标描述,经计算正常状态为2.983,行星轮缺齿状态为4.925。综上可证,通过声学信号的时域能区分故障状态与正常状态。
在已验证具有一定可分性的前提下,为避免因降噪、域变换等过程导致信息损失、微弱特征被忽略,本文不对声学信号进行预处理,而是直接将声学信号时域作为所提诊断网络的输入,实现端到端的故障诊断。
2.2 电机电流信号预处理
行星齿轮箱与电机相连,当行星齿轮箱中部件出现故障时,机组系统会产生额外的扭矩波动[28],然后电机会产生相应的扭矩来平衡该扭矩波动,进而反映为电机的电流变化[29]。因此能够通过电机电流信号诊断行星齿轮箱故障。
但与声学信号不同,故障状态与正常状态下的电机电流时域信号和直接对时域信号作快速傅里叶变换(Fast Fourier Transform,FFT)获得的频域信号都有极大局限性,可分性差。
仍以行星齿轮箱中行星轮缺齿故障为例进行分析。图3为正常状态电机电流信号时域和频域图。图4为行星轮缺齿状态电机电流信号时域和频域图。对比可知:二者时域信号的周期和幅值几乎一致;频域信号也仅电流工频突出,幅值稍有差异,无与行星轮故障相关的特征。

图3 正常状态电机电流信号时域和频域图Fig.3 Time and frequency domain diagrams of motor current signal in normal state

图4 行星轮缺齿状态电机电流信号时域和频域Fig.4 Time and frequency domain diagrams of motor current signal in epicyclic gear teeth missing state
因此,需对电机电流信号进行预处理,使故障特征突出并增强可分性。首先,采用经验模态分解(Empirical Mode Decomposition,EMD)把电机电流信号分解为一簇IMF分量,使复杂的非平稳信号变为单分量。然后,对获取的IMF分量作快速傅里叶变换。以所示行星轮缺齿故障为例,如图5所示,IMF1~IMF3依然是仅电流工频fe突出,故障相关特征不明显;IMF4中除电流工频突出外,与行星轮故障相关的特征均较明显,如行星轮故障频率fp以及0.5fp、fe-0.5fp、fe+0.5fp都较突出,而且幅值都高于正常状态(见表1),约是正常状态的1.6~2.2倍。

表1 行星轮故障特征频率幅值Table 1 Fault feature frequency amplitude of epicyclic gear

图5 行星轮缺齿状态电机电流EMD分解频域图Fig.5 EMD decomposition frequency domain diagram of motor current signal in epicyclic gear teeth missing state
综上分析,确定将IMF4分量频域信号作为所提诊断网络的输入。
2.3 多尺度解耦卷积网络构建
由于声学信号和预处理后的电机电流信号均是一维,所以本文构建的2种非接触传感器信号深度特征融合诊断网络以一维标准卷积网络为基础。
但标准卷积网络对类间差异不够敏感,易混淆类内变异和类间差异,因此引入双曲正切解耦卷积对标准卷积网络进行改进,将其置于网络最开始,用以在声学和电机电流信号中提取微弱、对类间差异敏感的特征。此外,故障影响声学信号和电机电流信号的机理不同,使得2种信号对同一故障的描述具有互补性,所以通过双曲正切解耦卷积分别对2种信号进行独立的特征提取,以保持互补关系。
对2种信号独立的特征提取采用了多尺度的解耦卷积,通过2个大小不同的卷积核进行解耦卷积操作,以获取到稀疏和不稀疏2种尺度的特征,增加感受野。再将2种尺度特征进行串行计算,然后进行池化和再次的解耦卷积,进一步扩大类间差异。接着把经过解耦卷积后获取的2种信号的特征作并行计算,并通过池化和标准卷积实现特征整合。之后引入金字塔池化模块来减少整合后特征的丢失,形成一个轻量化的多尺度解耦卷积网络。具体结构和详细参数如图6和表2所示。

表2 多尺度解耦卷积网络详细参数Table 2 Detailed parameters of multiscale decoupling convolution network

图6 多尺度解耦卷积网络详细结构Fig.6 Detailed structure of multiscale decoupling convolution network
3 试验验证
3.1 试验设计
试验所用行星齿轮箱系统如图7所示,包括机械部分和采集部分。机械部分主要由磁粉制动器、行星齿轮箱和电机组成。行星齿轮箱内部结构如图8所示,主要由齿圈、太阳轮、太阳轮轴承、行星轮、行星轮轴承等组成。采集部分主要由数据采集器、笔记本电脑和多种传感器(即声学、电流和振动加速度传感器)组成。

图7 行星齿轮箱试验系统Fig.7 Epicyclic gearbox testing system

图8 行星齿轮箱内部结构Fig.8 Internal structure of epicyclic gearbox
试验时,将声学传感器置于行星齿轮箱垂直径向上方处,将电机电源线穿过电流传感器,将振动传感器安装于行星齿轮箱垂直径向位置,之后3个传感器通过信号线与数据采集器相连,再通过计算机实现数据的同步采集和控制。
行星齿轮箱试验条件设计为:转速2 400 r/min,负载9 N·m,采样频率12 kHz。设置的状态有6种,既包含单一故障,还包含耦合故障,具体如表3所示。其中,耦合故障是以上单一故障的复合,复合方式如图9所示,其故障特征与单一故障特征近似,能有效检验所提方法的效果。
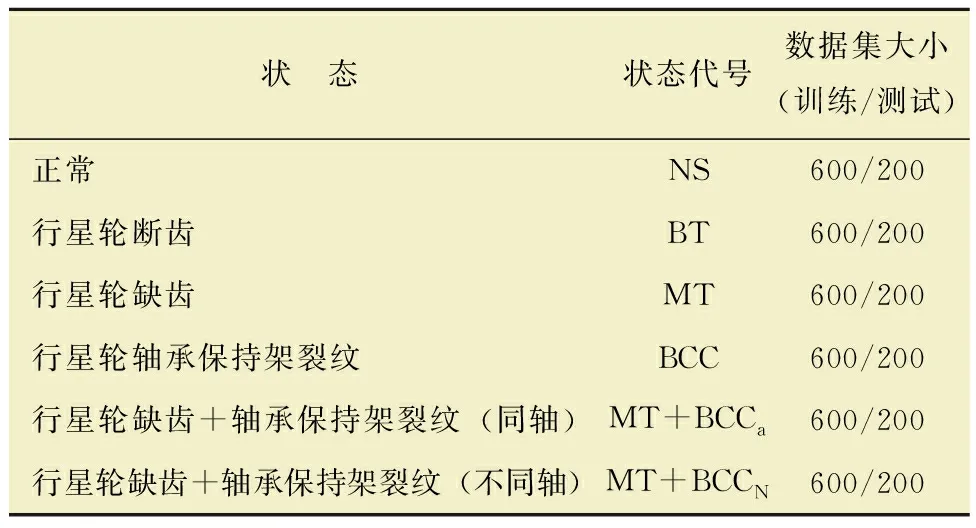
表3 行星齿轮箱故障状态Table 3 Fault state of epicyclic gearbox
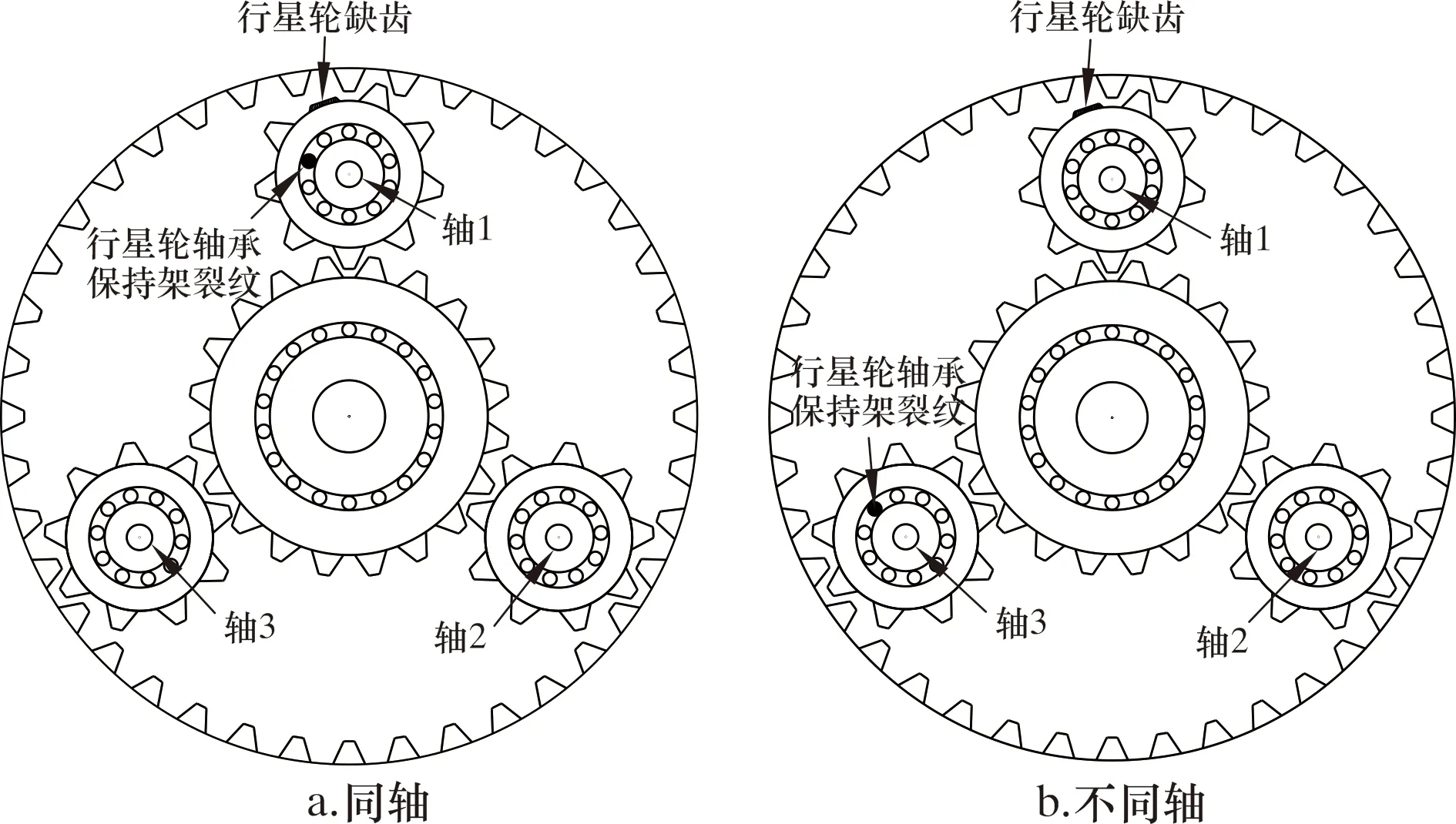
图9 耦合故障(行星轮缺齿+行星轮轴承保持架裂纹)复合方式Fig.9 Composite mode of coupling fault (epicyclic gear teeth missing + epicyclic gear retainer crack)
数据长度为1 024,训练数据和测试数据按3∶1的比例划分,每种状态训练数据600组,测试数据200组,因此6种状态共有训练数据3 600组,测试数据1 200组。
3.2 试验对比和结果分析
3.2.1 解耦卷积层与标准卷积层比较
为对比解耦卷积层与标准卷积层的效果差异,将声学和电机电流信号输入至所提网络和与所提网络结构一致但不含解耦卷积层的网络中,同样迭代30次,迭代曲线如图10所示。由图10可见:不含解耦卷积层的网络在迭代结束时才趋于收敛,曲线整体波动性大;而含解耦卷积层的网络在第10代时就趋向于收敛,且曲线波动较小,最后的诊断准确率也更高。说明解耦卷积有效地提取了类间差异敏感的特征,进而加速了网络收敛。

图10 准确率曲线Fig.10 Accuracy curve
3.2.2 与单一非接触传感器诊断、标准卷积网络融合诊断对比
为检验所提网络融合诊断的效果,将其分别与单一非接触传感器诊断、标准卷积网络融合诊断作对比,即分别将单一声学信号、单一电机电流信号、声学和电机电流信号分别输入至改进前的标准卷积网络中。为保证结果的准确性重复测试了5次,5次测试的结果如图11和表4所示。结果表明,本文所提网络各次测试的准确率均最高,平均诊断准确率比仅声学、仅电机电流、标准卷积网络融合声学和电机电流信号分别提高8.67个百分点、6.13个百分点和4.93个百分点。此外所提网络的标准差较小,表明该方法的稳定性也较好。

表4 5次测试的平均准确率和标准差Table 4 Average testing accuracy and standard deviation

图11 5次测试详细的测试准确率Fig.11 Detailed testing accuracy of 5 tests
图12为通过t-分布邻域嵌入法(t-distributed stochastic neighbor embedding,t-SNE)对以上诊断方法的可视化,能更清晰分辨不同方法对各状态的区分情况。图12显示,采用单一非接触传感器诊断和2种非接触传感器信号通过标准卷积网络融合诊断时,均未能实现对6种状态的完全正确分类。仅声学信号(见图12a)时,缺齿、保持架裂纹、缺齿和保持架裂纹的耦合故障间无明晰界限,尤其2种耦合故障存在大量重叠;仅电机电流信号(见图12b)时,各状态均未能完全聚为一团,其中故障程度相对不严重的轴承保持架裂纹与正常状态混叠,缺齿和保持架裂纹的耦合故障与缺齿状态也存在混叠,其余状态间亦无明晰界限。
综上,仅单一非接触传感器无法全面描述故障。声学和电机电流信号通过标准卷积网络融合(见图12c)时,部分相似状态仍存在极小的混叠,基本上各状态都能聚为一团,但聚集得较为松散,且各状态间距离较近,表明类内变异较大,类间差异较小。图12d为本文所提网络诊断结果的可视化,6种状态已被完全地分开,同类状态紧凑地聚在一起,不同类状态相距较远(由坐标可知),表明所提网络有效地缩小了类内变异,扩大了类间差异,尤其对于相似的耦合故障。同时具象化地表明了所提的多尺度解耦卷积网络实现融合诊断的优越性。
3.2.3 与接触传感器(振动传感器)诊断对比
本研究是为了在接触传感器安装受限时仍能实现行星齿轮箱故障诊断,因此需对比所提方法与接触传感器(即振动传感器)的诊断效果,衡量本文所提方法的可行性。
将振动信号输入至改进前的标准卷积网络中,5次测试的结果如图13所示。

图13 5次测试的详细测试准确率及其平均值Fig.13 Detailed testing accuracy and average of 5 tests
由图13可知,所提方法每次测试准确率均高于振动,平均约提高了2.66个百分点。在训练时间方面,振动信号诊断法平均约需6.78 s,本文所提方法平均约需11.46 s,差距较小。
为具体分析2个方法对6类状态诊断的效果,绘制如图14所示的混淆矩阵以进行定量比较,其中纵坐标为真实状态,横坐标为诊断状态,对角线上数据为诊断正确率,其余位置数据为错误率。从图14a可知,振动信号诊断将约9%的“缺齿和保持架裂纹(同轴)”耦合故障误诊为“缺齿和保持架裂(不同轴)”耦合故障,表明其对类间差异较小的2类耦合故障不敏感,而本文所提方法则对此有优异效果。从图14b可知,对“缺齿和保持架裂纹(同轴)”耦合故障诊断准确率可达99%,充分证明所提方法能有效提取故障特征,且充分关注类间差异,实现相似状态的准确诊断;此外还表明2种非接触传感器融合后不仅能达到与接触传感器一样好的诊断效果,而且实现了小幅度提高。

图14 混淆矩阵Fig.14 Confusion matrix
3.2.4 抗噪性分析
室内试验采集的声学和振动信号受噪声影响较小,真实环境中二者受噪声影响较大。为使试验数据更符合现场数据,向试验声学和振动信号中加入不同强度的高斯白噪声,加噪后信号的信噪比RSN为-6~6 dB,间隔为2 dB。信噪比定义公式为:
(8)
式中:Ps为信号有效功率;Pn为噪声有效功率;RSN单位为dB。
此外,在真实环境中很难获取不同强度噪声下带标签的故障数据。为能更贴近该情况,诊断网络的训练采用试验信号,测试采用加噪后信号。
图15所示为不同信噪比下诊断网络的准确率。由图15可以看出:仅振动和仅声学的诊断准确率曲线趋势都陡峭,伴随信噪比的减小,即噪声强度不断增大,准确率显著下降,说明二者的抗噪性差;而本文方法诊断准确率曲线趋势平稳,在信噪比达到-6 dB时准确率仍大于85%,且当信噪比逐步增大,准确率稳定在98.0%。这说明本文方法良好地完成了声学与电机电流信号特征融合,使易受噪声污染的声学信号与不易受污染的电机电流信号实现有效互补,因此具有了较强的抗噪能力。

图15 不同信噪比下诊断准确率Fig.15 Diagnostic accuracy at different signal-to-noise ratios
3.2.5 与同类其他方法对比
本文所提方法与同类其他的卷积网络AlexNet-8、VGG16、InceptionV1-22和ResNet18进行比较。将声学和电机电流信号输入至4种网络中,通过诊断准确率、参数量(Params)、FLOPs和训练时间4个指标评价不同方法的优劣。其中参数量和FLOPs是判断网络是否轻量化的2个重要评价指标。试验结果如表5所示。
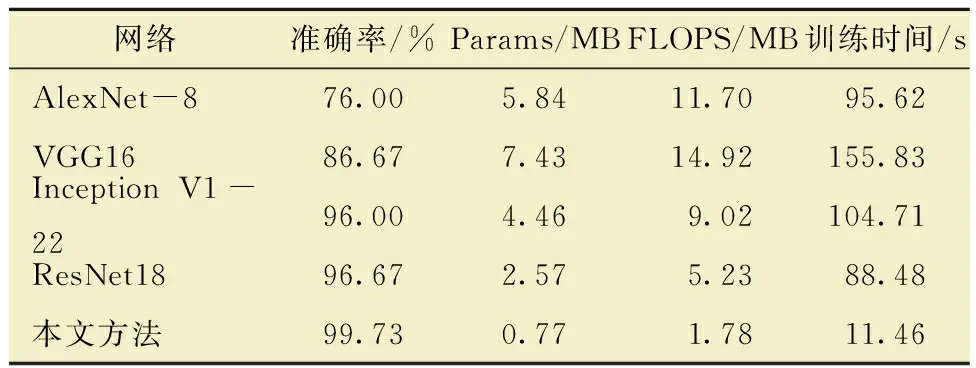
表5 与同类其他方法结果对比Table 5 Comparison of results with other similar methods
对比发现,在相同的迭代次数中,本文方法所需时间最少,准确率最高,且衡量网络内存需求的参数量指标和网络复杂度的FLOPs指标也均为最小。这说明本文所提网络是轻量化的,其结构相对简单、复杂度低,计算效率高,更有望被部署。
4 结 论
(1)采用解耦卷积层代替标准卷积层提取声学信号和电机电流信号中故障特征,能有效挖掘微弱、对类间差异敏感的特征。与只含标准卷积层的同结构网络相比,改进后提前了15代趋于收敛。
(2)采用对类间差异敏感、能增大感受野的多尺度解耦卷积和能减少特征丢失的金字塔池化模块改进标准卷积网络,形成多尺度解耦卷积网络,提高融合诊断效果。相比标准卷积网络和同类结构较深的网络,该网络准确率更高、训练时间短,且参数量和FLOPs更小,仅为770 kB和1.78 MB,是一个轻量化的网络,更有望被部署。
(3)采用2种非接触传感器融合诊断,能适用接触传感器安装受限的情况。该方法取得了比接触传感器诊断更高的准确率(提升了约2.66个百分点)和更好的抗噪性能(信噪比达到-6 dB时准确率仍大于85%,远大于接触传感器的54.4%);同时该方法故障诊断效果也优于单一声学、单一电流传感器,平均诊断准确率分别提升8.67和6.13个百分点。
