基于不同变形模式耗能框剪结构地震响应分析

罗维刚,祁 盼,宋江朋,李兰舟

(1.西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州 730050;2.甘肃省土木工程防灾减灾重点实验室,甘肃 兰州 730050; 3.兰州理工大学 土木工程学院,甘肃 兰州 730050)

在地震作用下,传统框架剪力墙双重结构破坏主要集中在墙体与墙体、框架与墙体之间的连梁或楼板上。因此,国内外学者用各种耗能构件进行替换,实现耗能和韧性功能。吕西林等[1]提出了用于可更换连梁的三种保险丝,并通过试验验证了保险丝功能的可行性;黄海新等[2]提出一种L型的金属耗能器,其具有大位移的变形特点;周云等[3]提出了功能自恢复连梁;崔瑶等[4]对平板支座进行拟静力加载试验,并针对提高该耗能能力给出了改进方案;霍林生等[5]提出了一种轻型屈曲约束支撑;周云等[6]提出一种新型管铅阻尼器,通过数值模拟验证了其耗能的可行性;Li X等[7]提出了几种可替换消能减震钢连梁,研究表明可替换耗能梁段在大震作用下率先进入塑性变形耗散能量,保护承重结构,震后通过更换损伤的耗能构件,使结构迅速恢复使用功能[8-11]。

上述研究是在构件层面添加或替换耗能构件以提高消能减震能力的,但利用结构自身变形特性来降低抗震需求的研究却很少。本文基于双重结构体系[12]中两个分体系在地震作用下侧向变形模式的不同,提出一种在两分体系间设置屈曲约束支撑(BRB)的耗能结构,可以称为基于不同变形模式的耗能双重结构。以框架剪力墙双重结构为例,通过在框架与剪力墙之间施加BRB得到新型耗能框架剪力墙双重结构,简称耗能双重结构,即利用框架与剪力墙两个分体系在水平地震作用时的“剪切型”和“弯曲型”变形模式不同,在每个楼层处两分体系间设置BRB构件,使其利用框架与剪力墙的相对运动进行耗能,同时“切断”重力荷载框架产生的惯性力向剪力墙传递,且可以通过改变BRB构件刚度和强度参数控制传递能力,减小结构抗震需求。

本文建立了耗能双重结构强度模型,考虑了结构构件的塑性和混凝土开裂对混凝土构件刚度的影响,可以更加准确地模拟实际混凝土结构在地震作用下的动力响应。强度模型的建立是在剪力墙底部、框架柱端和框架梁端设置集中塑性铰模拟钢筋混凝土结构构件的非线性行为[13],通过动力非线性分析BRB的不同刚度和强度参数对耗能双重结构强度模型各项地震响应控制效果的同时,讨论剪力墙和框架结构抗侧移刚度相对变化对耗能双重结构体系抗震性能的影响。

1 数值分析模型

1.1 原型框架剪力墙结构的基本信息

原型结构为一个六层传统框架剪力墙结构,其中一个单元平面布置如图1所示。结构底层计算高度为5.1 m,标准层高为3.1 m。框架柱截面尺寸为700 mm×700 mm;框架梁截面尺寸为300 mm × 500 mm;连梁截面尺寸为300 mm×750 mm;楼板厚度150 mm;抗震设防烈度为8度,场地类别为Ⅱ类,抗震等级为三级,设计基本地震加速度为0.3g,设计基准期为50年,混凝土强度等级采用C35。

图1 剪力墙、梁、柱平面布置图

1.2 框架剪力墙结构的有限元分析模型

对原型结构用ANSYS建立2D模型,将电梯井周围剪力墙等效成一片总剪力墙,并均匀分配到三榀框架上,取其中一榀框架剪力墙结构建立有限元分析模型;考虑楼板对框架梁的影响以及刚性楼板假定,将框架梁截面刚度放大10倍来实现,楼板自重由密度输入考虑,而活荷载取一半,按照附属面积计算,采用集中附加质量源的办法施加在框架结构的梁柱节点上,分析模型如图2所示。

图2 2D有限元分析简化模型

BRB的屈服强度通过传统结构连梁内力计算确定,刚度取值考虑了框架与剪力墙侧向变形能力,由给定的屈服变形确定,具体如下:对传统框架剪力墙原型结构模型进行动力时程分析,求出剪力墙结构的基底剪力;将基底剪力沿结构高度按倒三角分配至各层,得到沿高度成比例的各层连梁内力,顶层连梁内力记为Fy;在新型耗能结构中顶层BRB屈服强度取为Fy,由于各层内力按倒三角成比例,此时Fy也代表了各层BRB的屈服强度大小;选取BRB的屈服变形为0.0035 m[14],并以此计算对应的初始刚度,初始刚度为屈服强度与屈服变形的比值,而屈服后刚度取为初始刚度的5%。本文将传统框架剪力墙结构计算得到的连梁内力等量对应的BRB屈服强度的分析模型定义为新型耗能结构的基准分析模型。

1.3 有限元分析模型单元选取和参数确定

1.3.1 单元选取

用Beam188单元模拟连梁、框架梁柱和剪力墙;Combine39单元[15]模拟BRB;框架梁的两端、框架柱和剪力墙底部分别设置集中塑性铰,采用Combine39单元模拟;Mass21单元模拟施加的折算活荷载。

1.3.2 塑性铰参数的确定

框架梁、柱与剪力墙集中塑性铰本构关系参考了NIST CR 17-917-45报告结果[16],充分考虑混凝土开裂引起的刚度折减,其范围在0.3EI～0.7EI,框架梁采用柱模型本构,但轴压比取为零。框架柱与剪力墙轴压比分别为0.49和0.36,具体取值见表1和表2所示。表1中的Mn为屈服弯矩,可由文献[17]计算得到。

表1 钢筋混凝土框架梁柱骨架曲线控制点[16]

表2 塑性铰本构模型参数

2 有限元分析

建立三种不同剪力墙与框架结构抗侧移刚度比的耗能结构强度模型,在研究不同BRB参数对结构动力响应影响的同时,分析结构两个分体系抗侧移刚度差异对耗能结构动力响应的影响。其中,模型1中剪力墙与框架的抗侧移刚度比为9.7∶0.3;模型2中剪力墙与框架的抗侧移刚度比为8.0∶2.0;模型3中剪力墙与框架的抗侧移刚度比为7.2∶2.8。三种模型BRB屈服强度取基准分析模型Fy的10%、15%、20%、25%、30%、33%、67%、100%、133%、167%和200%,共计11个参数工况进行。

2.1 地震波选取

本文选取地震波考虑了地震类型、卓越频率、震中距、脉冲效应等不同因素,从PEER强震记录数据库中选取了El-Centro波、Imperial Valley波、Taft波、Parkfield波、San Fernando波、Tabas波等六条波,将其峰值加速度调幅至设计基本地震加速度0.3g。加速度反应谱及位移反应谱如图3和图4所示。

图3 加速度反应谱

图4 位移反应谱

2.2 模态分析

对比固有频率和模态振型探讨不同变形模式新型耗能结构的耗能机理和相对变形模式。

2.2.1 模态对比

对传统结构强度模型和新型耗能结构强度模型进行模态分析,结果表明:新型耗能结构强度模型自振周期较传统结构强度模型相比有所延长,且新型耗能结构体系的框架与剪力墙除第一阶振型相对运动一致外,其他振型出现了不一致的相对运动,如第二阶振型表现为剪力墙一阶振动时框架以二阶振型振动,这进一步增大了个别楼层两者的相对变形。表3为10%FyBRB新型耗能结构与传统结构的强度模型两阶自振周期对比,振型如图5所示。

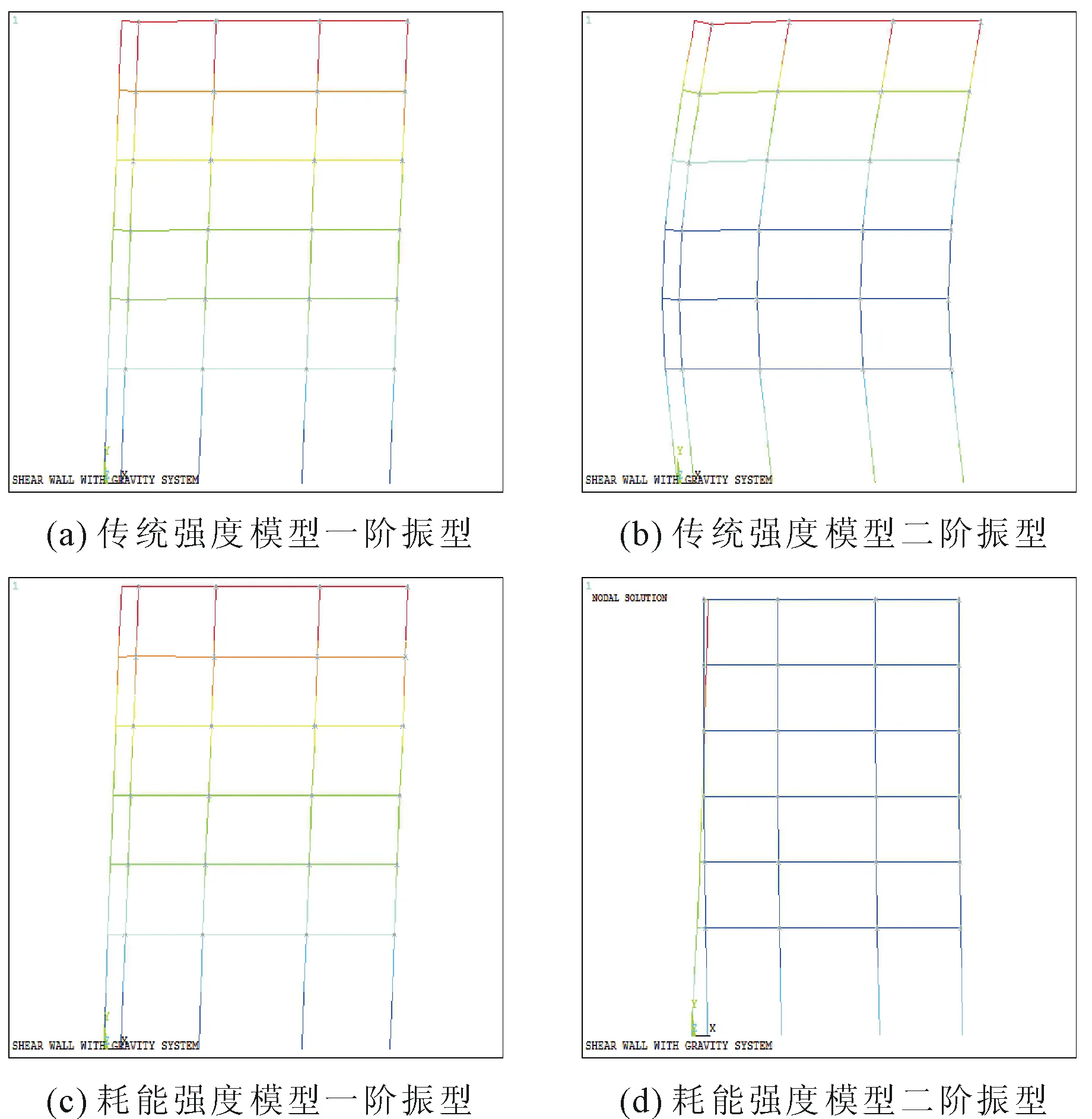
图5 传统强度模型(图a、图b)与耗能强度模型(图c、图d)振型

表3 两种结构自振周期对比

2.2.2 不同刚度比的BRB耗能结构强度模型模态对比

从上节可知,框架与剪力墙振动时相对侧向变形大小是BRB能否高效工作的关键,因此本文还考察了剪力墙和框架结构抗侧移刚度相对变化对BRB耗能敏感性的影响。通过对三种不同剪力墙与框架抗侧移刚度比耗能结构强度模型分析,选取安装有10%FyBRB的耗能结构强度模型进行模态分析对比各自的自振周期、振型。结果表明:随着刚度比的减小,模型的结构周期逐渐增大(见表4),说明刚度比对结构周期较为敏感。从图6可知,从模型1到模型3,剪力墙与框架抗侧移刚度比减小,两者的不一致性变形减少。

图6 三种不同刚度比模型振型对比

表4 三种不同刚度比模型自振周期对比

2.3 非线性动力时程分析

本节对不同BRB设计参数和刚度比的耗能结构强度模型和传统结构强度模型,输入6条地震动进行非线性动力时程分析,计算得到峰值加速度、基底剪力、侧向位移及层间位移角,并讨论耗能结构响应与传统结构响应比值随BRB参数变化的规律,分析剪力墙与框架抗侧移刚度比对耗能结构体系动力响应的影响。

分析结果以图表的形式给出,并对其内容作如下说明:(1)横坐标为传统结构强度模型和不同BRB取值的新型耗能结构强度模型;(2)纵坐标为新型耗能结构强度模型响应与对应传统结构强度模型响应的比值,若该比值小于1,表明耗能结构强度模型的该响应小于传统结构强度模型的响应。

2.3.1 剪力墙动力响应分析

框架剪力墙结构中框架承担了主要的竖向重力荷载,并在地震作用时产生主要的惯性力,因此框架与剪力墙之间的BRB具有将惯性力向剪力墙传递的“切断”效应。结果表明:(1)三种模型中剪力墙的峰值加速度、基底剪力均有所下降,但侧向位移增大;(2)三种模型剪力墙峰值侧移均大于传统结构且在10%Fy处最大,分别增大约7%～15%(图7所示);(3)在BRB屈服强度取10%Fy～200%Fy范围内时三种模型的剪力墙峰值加速度、基底剪力均小于传统结构,且加速度响应与基底剪力响应比值分别随着BRB的增大呈先减小后增大的变化趋势;在BRB取10%Fy～33%Fy时响应有明显的减小;当BRB取值为10%Fy时响应最小,分别减小了20%～35%和55%～60%(图8—图9所示)。由此可见,BRB“切断”了框架产生的惯性力向剪力墙的传递,使其加速度、基底剪力相应减小。

图7 剪力墙峰值侧移随BRB变化

图8 剪力墙峰值加速度随BRB变化

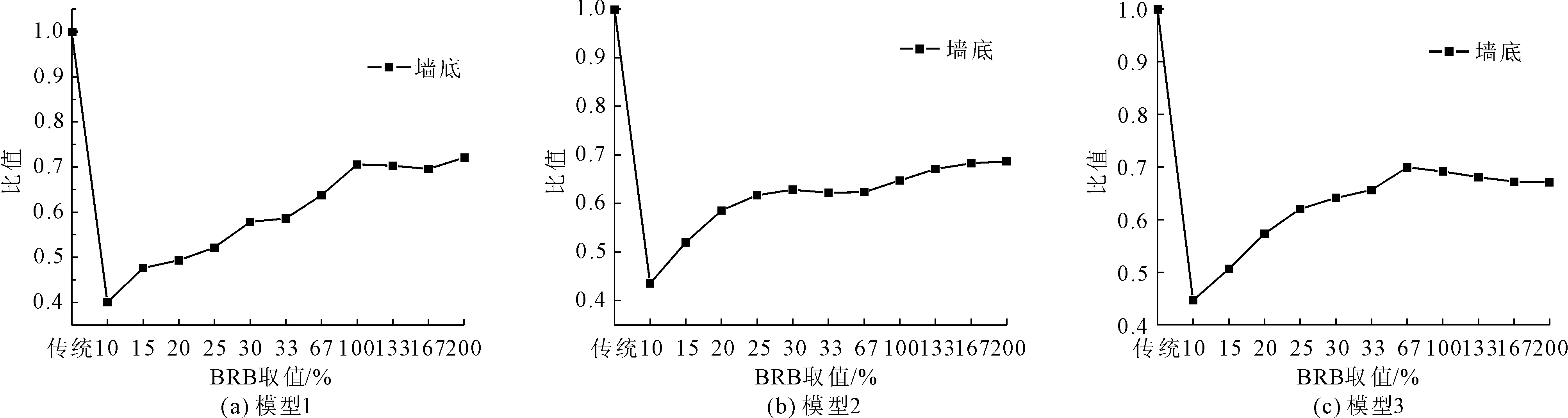
图9 剪力墙基底剪力随BRB变化

2.3.2 框架动力响应分析

BRB的参数对耗能结构动力响应有明显的影响,通过对11个参数工况的分析,得到6条地震动作用下框架结构峰值加速度、基底剪力、柱底弯矩、各层侧移以及层间位移角数据。由图10可知三种不同抗侧移刚度比模型中框架峰值加速度响应随着BRB屈服强度(初始刚度)增加表现出先减小后增大趋势,在10%Fy～33%Fy范围各层响应比均小于1,且在BRB取值为10%Fy时响应比为最小,表明BRB屈服强度约为10%Fy时耗能结构中框架峰值加速度响应比传统结构中框架减小了约25%～30%。框架结构基底剪力(图11)和框架柱底弯矩随BRB参数的增大也呈先减小后增大的趋势,而且均在10%Fy处响应最小,分别减小了60%和40%。

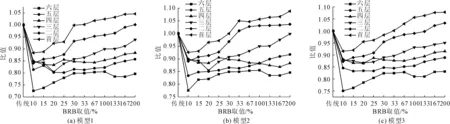
图10 框架峰值加速度随BRB变化

图11 框架基底剪力随BRB变化

耗能结构与传统结构相比,框架结构各层侧向位移在三个模型中均有所增加(图12所示),最大为18%,这是因为:(1)考虑了地震作用下结构中混凝土开裂引起的结构刚度下降;(2)BRB的设置使得剪力墙与框架结构之间的约束作用减弱,两个分体系突出了各自的悬臂属性,更容易发生侧向变形;(3)位移型耗能单元BRB的变形也会引起整体结构刚度减小。

图12 框架峰值侧移随BRB变化

图13给出了传统结构强度模型和BRB屈服强度取值为10%Fy～33%Fy范围的三种模型的各层层间位移角,结构表明:层间位移角数值分别为0.0135、0.0136和0.0137,其中最大值均出现在第二层。虽然侧向位移有所增加,但当BRB取值为10%Fy～33%Fy范围时,仍满足弹塑性层间位移角限值0.02的规范要求。

图13 不同BRB取值结构弹塑性层间位移角对比示意图

2.4 不同抗侧移刚度比对结构地震响应影响分析

框架和剪力墙的相对运动与各自的抗侧移刚度有关,因此本文提出了三种不同抗侧移刚度比模型,分析讨论两分体系刚度对整体结构响应的影响。

2.4.1 顶层侧向位移对比及层间位移角对比

如图14和图15所示,三种模型剪力墙和框架顶层侧向位移均比传统结构有所增大,模型2增加幅度最小,模型3最大,其中剪力墙和框架顶层位移增加幅度最大分别为14%和16%。

图14 剪力墙顶层侧移对比

如图16所示,从模型1到模型3的层间位移角比值最大依次为1.088、1.101和1.108,即随着刚度比的增加位移角比值在逐渐减小,表明刚度比的增加有利于控制层间位移角的变形。

2.4.2 各层峰值加速度对比

三种模型框架各楼层峰值加速度响应随着BRB屈服强度的增加先减小后增大(如图10所示),变化趋势相同;三种模型顶层峰值加速度响应对比见图17所示,模型1降低最为明显。剪力墙各层峰值加速度新型耗能结构比传统结构均有所减小(如图8所示),展现了明显的“切断”效应,但就减小程度而言,模型1则表现更为突出,如图18所示,顶层峰值加速度最大降低了25%。结果表明,当剪力墙与框架的抗侧移刚度比较大时对耗能结构减小峰值加速度响应更有利。

图17 框架顶层加速度对比

图18 剪力墙顶层加速度对比

2.4.3 峰值基底剪力对比

三种模型的峰值基底剪力随着BRB屈服强度的变化如图19和图20所示,表现为随着BRB屈服强度的增加先减小后增大。结果表明:当BRB屈服强度取值为10%Fy～33%Fy范围时,模型1的剪力墙和框架峰值基底剪力减小程度最大,比传统结构降低了约60%。

图19 剪力墙基底剪力对比

图20 框架基底剪力对比

对比三种模型各项响应发现:(1)侧移响应均有所增大,但剪力墙与框架抗侧移刚度比较大时,增大幅度较小;(2)抗侧移刚度比的增大有利于减小层间位移角响应;(3)峰值加速度和基底剪力响应均有不同程度减小,但剪力墙与框架抗侧移刚度比较大时,减小程度更加明显。

基于不同变形模式耗能双重结构不仅可以用于框架剪力墙结构,同样可以在框筒结构、框架支撑结构及双塔连体结构等双重结构中推广。

3 结 论

根据提出的基于不同变形模式耗能框架剪力墙耗能双重结构,建立了三种不同剪力墙与框架抗侧移刚度比的整体结构强度模型,通过非线性动力时程BRB参数分析,得出以下主要结论:

(1) 耗能双重结构比相应传统结构周期有所增长;与传统结构相比出现了两个分体系模态变形不一致的变形模态,进一步提高了BRB的耗能效果。

(2) 耗能双重结构在BRB屈服强度取值传统结构连梁内力的为10%～33%时,峰值加速度、基底剪力、基底弯矩响应与相应传统结构相比均明显减小,尤其剪力墙结构响应减小更为明显,表现出重力框架引起的惯性力向剪力墙传递时被“切断”机制。

(3) 耗能双重结构相比传统结构,框架侧向位移响应有所增大,但经合理设计BRB参数层间位移角可以控制在规范限值内。

(4) 耗能双重结构的剪力墙与框架抗侧移刚度比越大时,峰值加速度和基底剪力响应减小越明显,且侧向位移增大幅度较小,更利于减小层间位移角响应,结构耗能效果越好。