工质密度和储层渗透率演化对EGS系统传热效能的影响

黄涵钗,孟凡震,李沐子,修占国,张树翠,李致远

(青岛理工大学,山东 青岛 266000)

在所有清洁能源中,地热资源以其储量大、范围广、绿色清洁的特点备受青睐,被视为化石能源枯竭后最具潜力的战略接替能源[1]。其中人类能利用的地热资源90%都来自于干热岩[2]。目前干热岩的热能主要通过增强型地热系统(Enhanced Geothermal System,下简称EGS)开发,进行热能开采时,先从注入井泵入高压冷水,高压冷水流过热储干热岩中的裂缝,吸收岩石的热量,直到被迫以高压热蒸汽或汽水混合物的方式从生产井出来,实现采热。EGS的寿命以冷却区到达出口为止,此时称热贯通或热突破[3-4]。维持流体采热及延缓热突破是EGS系统的关键,直接影响EGS系统的产能和寿命。

流体进入地热储层后的流动和采热过程包含了复杂的热流固耦合效应,而热流固耦合效应必然导致流体密度和渗透率的演化,进而影响流体的采热和储层的热突破。针对这一现象,目前国内外学者基于数值模拟开展了大量耦合研究,其中大多数是基于商业软件实现的,其热流固耦合考虑的耦合项不完整[5-8],或者仅为建立在预先设定的耦合变量上的间接耦合,即不同物理场的求解系统是独立的[9-10],这一定程度上影响了耦合结果的准确性。少数EGS系统的热流固耦合模拟是基于自编程程序实现的。与商业软件基于正压流体模型建立的耦合程序不同,这些都是基于斜压流体密度模型建立的THM完全耦合自编程程序。Salimzadeh等[11]基于CSMP++设计了含单裂隙的热储层THM直接耦合程序,并基于立方定律探讨了裂隙渗透率演化对裂隙温度的影响。Cui Xin等[12]开发了等效多孔介质模型的THM双向耦合程序,并探讨不同耦合模式对收敛性的影响,结果表明了HM-T的双向耦合在保证耦合结果准确性的同时,可以比THM的直接耦合有更好的收敛。不过,对于方程中还残余的流体实时密度与参考密度之比,为了在计算流固场的耦合系数矩阵时,利用对称性来减少计算量,则忽略了实时流体密度的变化,这实际上是对流体密度演化的不完全实现。斜压流体密度模型在正压流体模型基础上进一步考虑了温度对于流体密度的影响,实现了求解系统中THM不同主要变量之间的直接耦合,更加符合实际情形。总体来说,基于斜压流体密度模型的THM完全耦合目前应用不多,基于该模型的传热效能分析也鲜有报道。

综上,为了提高EGS储层传热效能评价的准确性,本文建立包含传热效能指标评价的HM-T的双向耦合自编程程序,探究THM完全耦合作用下流体密度演化、渗透率演化对EGS系统和传热性能指标的影响。

1 THM耦合的数学模型

1.1 控制方程

对于变形场,基于饱和多孔弹性介质的应力平衡,建立了热弹性力学模型。在小变形假设下,考虑温度应力和孔隙压力的准静态条件下的应力平衡模型由式(1)给出:

(1)

式中:D为弹性张量;βv为多孔介质的体积热膨胀系数;Ks为多孔介质的体积模量;f为体力;未知量u为变形张量,T为温度,p为孔压;α表示Biot液力耦合系数;二维时,I=[1 1 0]T。

利用关于温度和压力的一阶泰勒展开式与参考流体密度ρf 0可以近似表征斜压流体的实际密度ρf。其中ρp和ρT分别为流体的体压缩系数和热膨胀系数。

ρf 0+ρf 0βp(p-p0)-ρf 0βT(T-T0)

(2)

则斜压流体在多孔介质内达西流动时的控制方程由式(3)给出[12]：

(3)

对于传热场,假设岩石基质中的流体速度足够慢,使得岩石基质中固体颗粒和流体始终处于局部热平衡。此时,用统一的变量表征多孔介质流体和固体的温度时,其传热的物理模型如式(4)[12]：

(4)

其中,

(ρc)m=φρfcf+(1-φ)ρscs

(5)

λm=φλf+(1-φ)λs

(6)

(7)

考虑渗透率演化时,使用李盼[13]基于室内实验得到的花岗岩渗透率演化模型对EGS系统进行模拟。

k=k0e0.23pm-0.15pc-0.0023Ts-0.21Tin

(8)

式中:pm为孔隙压力,MPa;pc为围压,MPa;Ts为岩样温度,K;Tin为注入温度,K。k0对应pm=0 MPa,pc= 0 MPa,Ts=0 K,Tin=0 K时的渗透率。不过这里不需要进行换算,实时渗透率k与k0之间是指数关系,使得k0可以认为是任意状态时的渗透率,k计算时仅需对pm、pc、Ts、Tin代入两状态间的增量即可。

1.2 EGS热开采的传热效能指标

生产井出口水温是评估EGS出力和寿命的重要指标之一[4,5,14]。出口平均水温定义为式(9):

(9)

式中:v为法向流速;T为温度;Γ为出口边界。

还有一些文献[13,15,16]定义净热提取率来讨论和评估不同输入参数下热提取效果。净热提取率是流经出口和入口的单位时间能量之差,通过式(10)得到:

Enet=Qouthout-Qinhin=cf(ρfoutvoutTout-ρfinvinTin)

(10)

式中:Qout、Qin分别为流出端和流入端工质的法向实时质量流率;hout、hin分别为流出端和流入端工质的实时比焓;ρfout、ρfin分别为流出端和流入端工质的实时流体密度;cf为流体工质的比热;Tout、Tin分别为流出端和流入端工质的温度。两种方法中,后者要实现更精确的计算还应当在THM耦合模拟中考虑比焓、相变等的变化,这里忽略相变,仅用比热和温度的乘积代替比焓。

1.3 THM耦合的程序实现

通过对控制方程组进行弱形式的推导,可以建立斜压流体THM完全耦合有限元模型,并进一步建立有限元程序。参考Cui和Wong[12],本文建立了基于等效多孔介质模型的HM-T的双向耦合求解有限元程序,如图1所示。

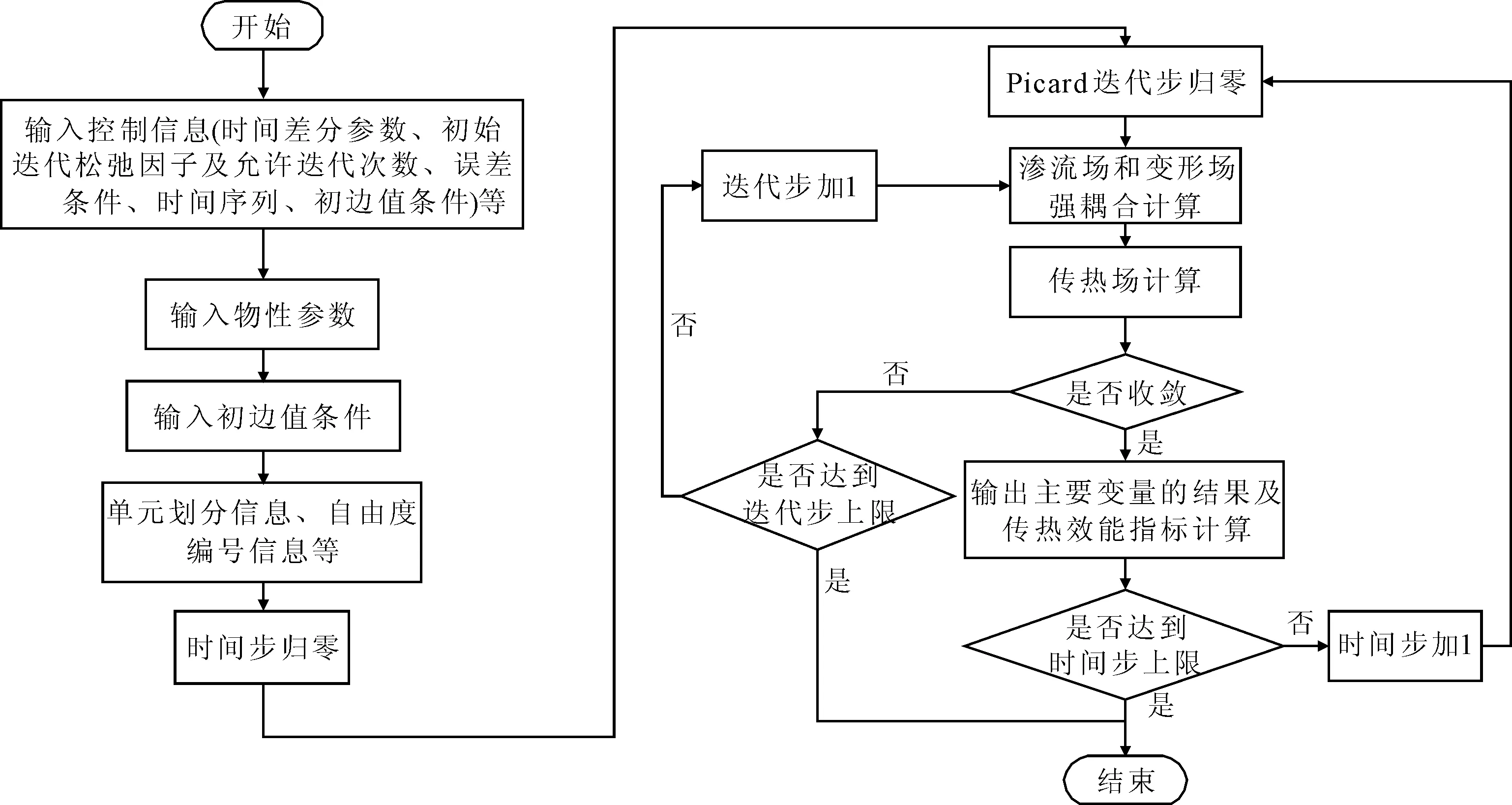
图1 HM-T的双向耦合求解有限元流程图

2 算例分析与讨论

2.1 计算模型及参数设置

本文使用的EGS模型基于Cui和Wong[12]的地热开采模型,见图2,原模型从五点注采模型中取了1/4进行了三维模拟。由于本文的有限元程序目前仅针对二维单元进行了开发,还未拓展到三维,本章在Cui等地热模型的基础上取A-A截面进行模拟。假设储层已经通过水力激励充分激发裂隙缝网,可以视作均匀等效连续介质处理。注入井流体出口位于储层左下角,而生产井流体入口位于储层右上角。

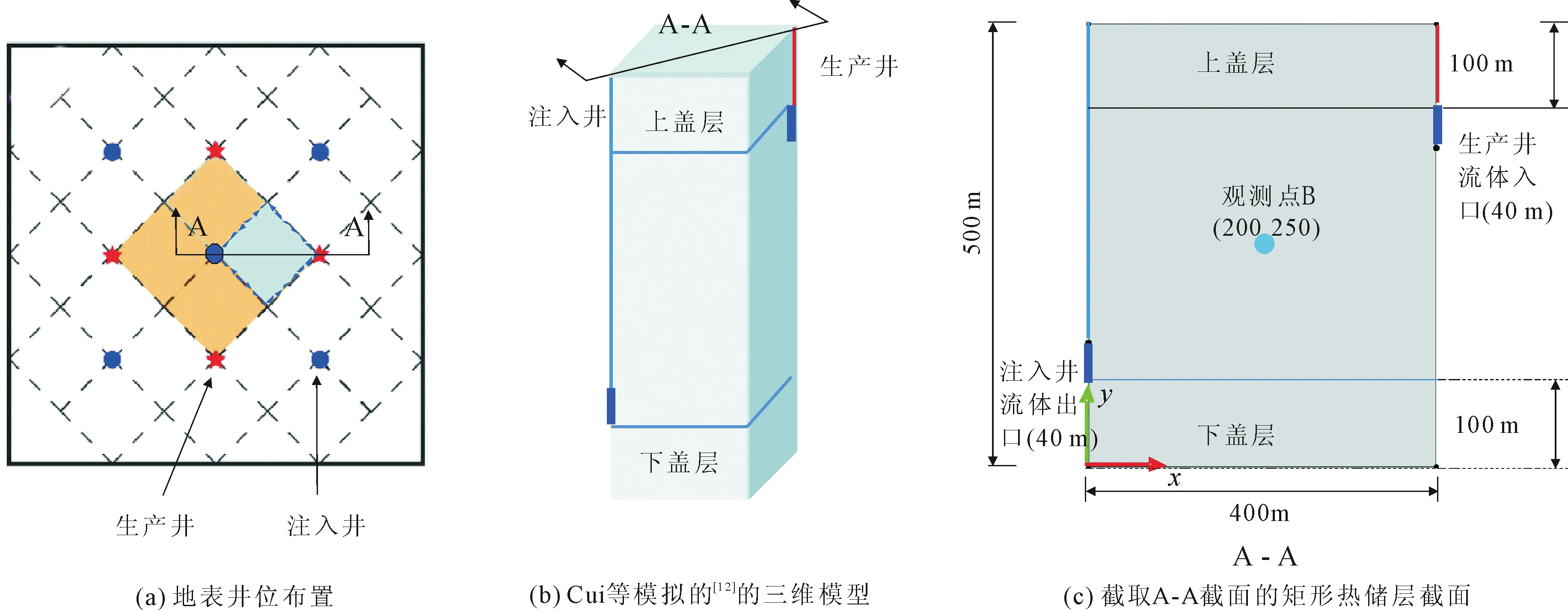
图2 五点注采模型

这里对EGS的模拟分两步进行,第一步仅对变形场和渗流场进行稳态计算,第二步以UP-T的双向耦合求解方式对储层模型进行持续40年的瞬态模拟计算。两步模拟的边界条件设置如图3。其中上边界σy=-25 MPa,对应地层深度约1 km,右边界σx=-37.5 MPa,即1.5倍竖直载荷。对于渗流场和温度场,未特殊说明的边界分别为不透水边界和绝热边界。假设以水为传热工质,但仅以20℃、0 MPa下的设置水流密度为1 000 kg/m3,其他输入参数见表1。单元设置为矩形单元,总计80(宽)×100(高)个。本文参考Cui和Wong[12],将瞬态模拟时间步长设计成序列形式,前100步的步长为0.01年,后390步的步长为0.1年。

图3 EGS储层模拟分两步进行的初边值条件

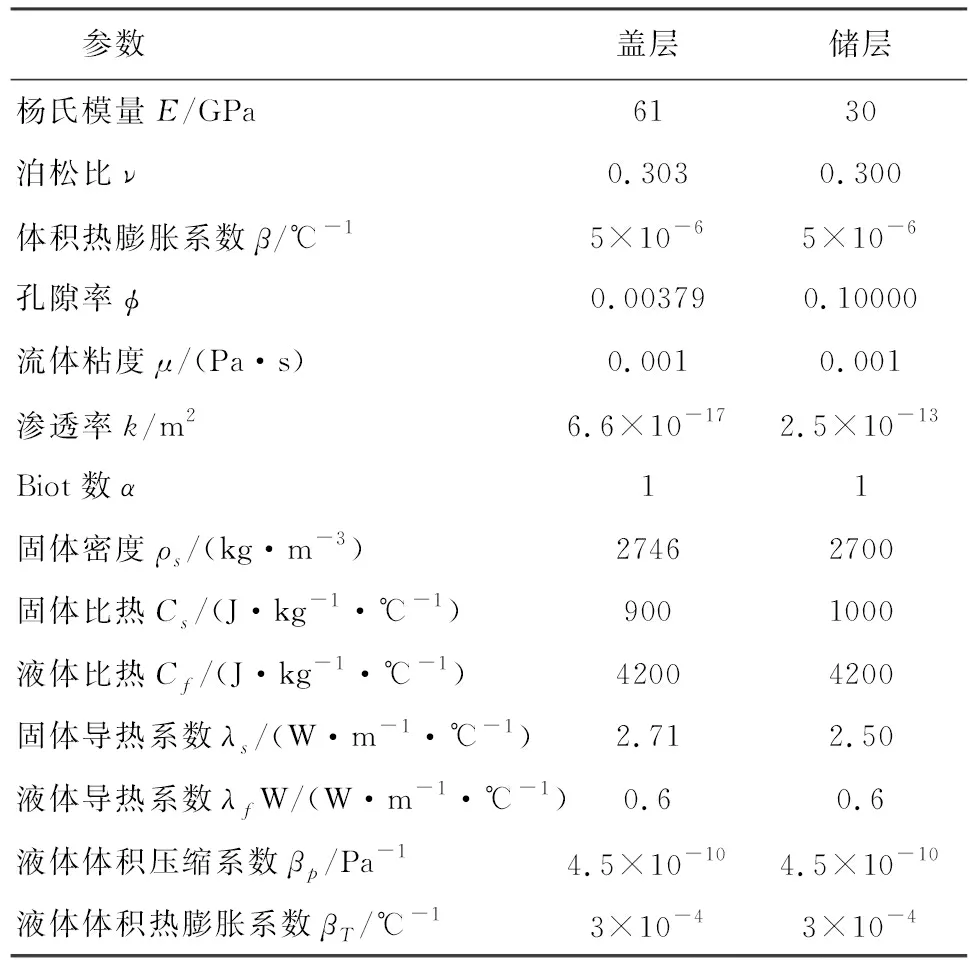
表1 地热开采模型中盖层和储层的输入参数

2.2 主要变量的时空演化特征

本文同时进行了考虑斜压流体密度演化和不考虑密度演化的数值模拟。不考虑流体密度演化时,认为流体密度为常数1 000 kg/m3。两种情况下主要变量的等值线形态相似。为避免赘余,在此仅绘制考虑斜压流体密度演化的模拟数据(0.01、1、10、20、30、40年后)进行观察,如图4所示。根据图4可以分析得到孔隙压力、温度、竖直位移、流体密度的时空演化特点如下:

图4 考虑流体密度演化时,40年内EGS模型的竖直位移v、孔压p、温度T、流体密度ρ演化

(1) 对于孔隙压力,在储层出口处的低压使得流体流出,区域内孔隙压力下降。周围流体向出口附近补充,来自渗透率较大的储层流体补充速度要比渗透率低的上盖层快得多;随着EGS运行,上盖层也有发生向出口的少量流动,使得孔隙压力逐渐演变,直至获得能够协调上盖层和储层不同渗透率的孔隙压力梯度分布。而在储层入口处,流体注入使得孔隙压力增大。总体来说,除了进出口处孔隙压力等值线稍微扭曲外,孔隙压力在空间分布上基本表现为沿竖直方向由下到上递减。

(2) 温度分布体现了对流占优型问题的明显特点,即存在完全冷却区且完全冷却区逐渐向出口扩张。完全冷却区逐步向出口扩散,其中上下盖层的渗透率较低,限制了从储层向上下盖层的流动,因此完全冷却区的扩散方向从入口处从水平向右,逐渐转为斜向上,最终指向出口。

(3) 对于竖向位移而言,储层和上盖层的竖向位移都是负值,即热开采导致了储层和上盖层的下沉。域内竖向位移的演化以完全冷却区的边界为界,完全冷却区两侧距离冷却区边界较远处,其局部变形几乎不受以温度梯度表征的热应力影响。完全冷却区的边界上,竖直位移等值线沿垂直于边界的方向扭曲。从地表上看,注入井和生产井的沉降量通常比其他区域多,开采初期,生产井由于需要提供低压而下沉显著;开采过程中,注入冷水导致注入井显著下沉,随开采进行,沉降逐渐从注入井扩散;从完全冷却区到达出口处(约第30年)开始,生产井的沉降量反而更显著。

(4) 对于流体密度而言,尽管依据斜压流体密度模型,温度和孔隙压力都会引起流体密度的变化,但是温度对流体密度的影响更大。具体体现在流体密度的等值线图中温度等值线图形状相同、趋势相反。在完全冷却区,流体温度较低,密度较大;在完全冷却区外,流体在流动过程中随着从岩层吸收热量其温度的升高,其密度也随之减小。总体来说,在密度演化模型下,实时流体密度比给定的常数密度(1 000 kg/m3)小。

2.3 流体密度演化对EGS系统的影响

在斜压流体模型中,流体密度的变化对热流固三个物理场的变量产生了影响。为探究这一影响规律,这里进一步绘制观测点B(见图2(c))处几个主要变量的变化如图5。基于孔隙压力的演化特点,可以将演化过程分为四个阶段。

(1) 第一阶段,即开始注入后0.01年内左右,由于此时出口处的孔隙压力条件比域内其他位置都小得多,较低的出口压力驱动流体克服重力向出口流动,域内的孔隙压力因此迅速下降。而此时完全冷却区还远在流体入口附近,变形场中有效应力仅随孔隙压力下降而增大,变形量增大,表现为水平和竖向位移向y轴负方向下降。考虑流体密度演化时,流体的孔隙压力下降的幅度比不考虑时大。这是因为考虑流体密度演化使得从B所在高度到出口处的流体实时密度比常数流体密度1 000 kg/m3小,维持从B到出口处的流动所需的压差比不考虑流体密度演化时小。

(2) 第二阶段,即完全冷却区到达B之前的阶段,从图5(c)和图5(d)可得这一时间大约在开始注入后的第0.1年至第12年。完全冷却区从流体入口处逐渐扩散导致储层温度降低。冷却区边界上的热应力作用使储层向流体入口处收缩,表现为水平位移和竖直位移的进一步减小。考虑流体密度演化与否对此时储层收缩的影响不大,且流体密度演化对完全冷却区的到达时间也没有显著影响。

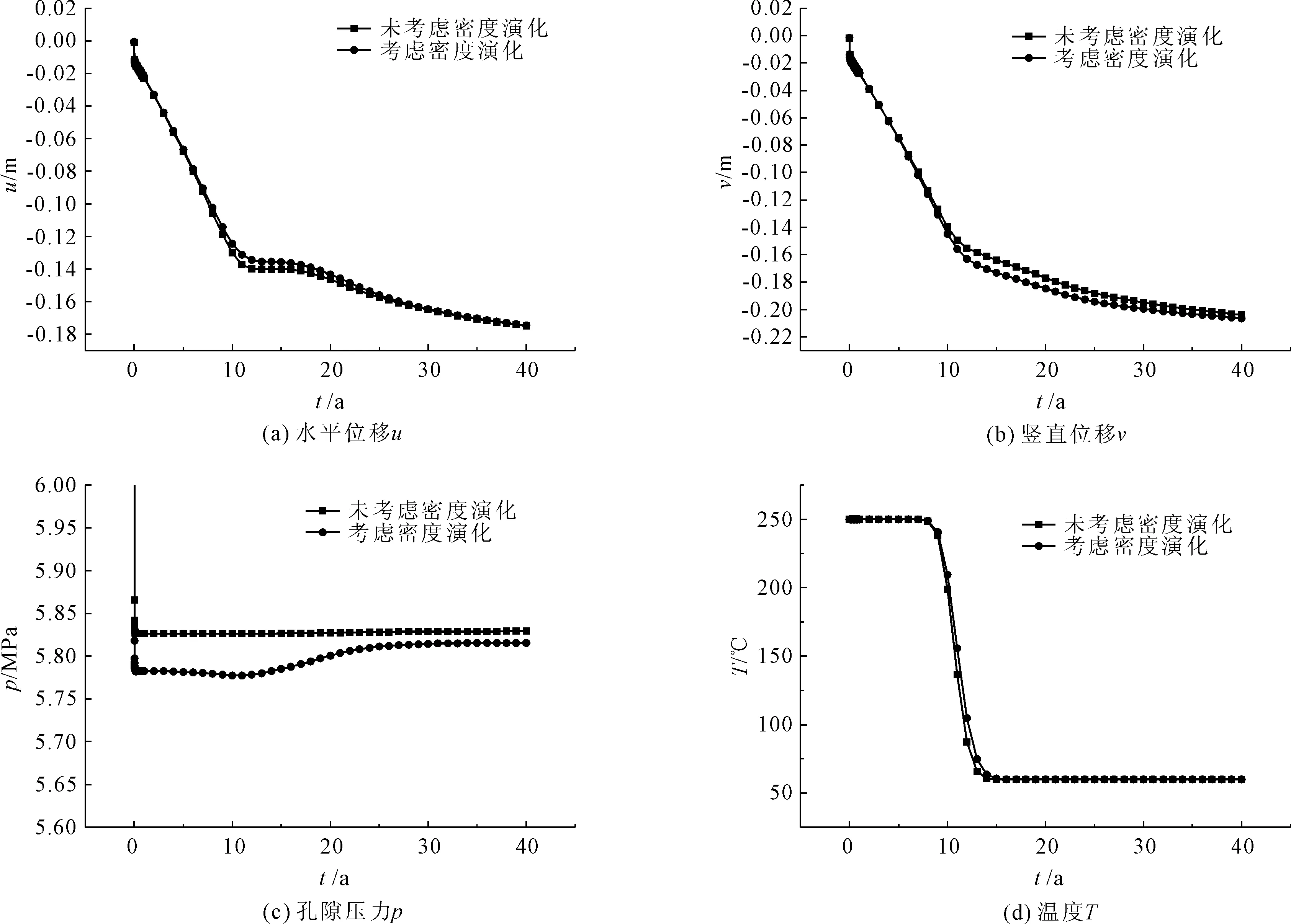
图5 考虑流体密度演化与否对模拟结果的影响

(3) 第三阶段,即完全冷却区从B扩张到出口处的阶段,结合图4和图5(d)可知这一时间大约在开始注入后的第12年至第30年。对于孔隙压力而言,考虑流体密度演化时,从在这一阶段开始,B所在高度以上的流体开始逐渐冷却而密度增大,从而维持到出口处的流动所需的压差增大,B处的孔隙压力开始增大。这一阶段还包含了B的冷却。从图5(d)可知B的冷却时间大约在始注入后的第12年至第19年。考虑流体密度演化时,B的冷却速度比不考虑密度演化时的慢一些。

(4) 第四阶段,即完全冷却区越过出口处所在高度后的扩张阶段,这一时间开始于注入30年之后,此时B至出口区域的流体密度基本稳定,故孔隙压力已不再受冷却区扩张的影响。

考虑密度演化与否对传热性能指标的影响见图6。如图6(a),尽管两者差距不太明显,但考虑密度变化比不考虑时延缓了出口温度的冷却。如果储层管理时设计某一标准如200℃作为合格的出口温度,考虑流体密度变化时储层寿命的模拟评估将比不考虑时延长近1年。对于净热提取率而言,如图6(b),开采的第一阶段EGS由于出口流速大而具有较高的净热提取率,进入稳定开采期后净热提取率演化主要受温度影响,净热提取率考虑密度演化时模拟评估净热提取率比不考虑时提高4.09%。

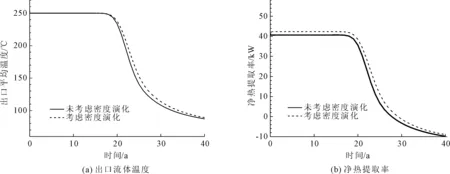
图6 考虑密度演化与否对传热效能的影响

2.4 流体密度和储层渗透率耦合演化对EGS的影响

这里初始状态对应第一步稳态计算后的状态,认为此时具有初始渗透率k0=2.5×10-13m2,此后储层渗透率因热流固耦合效应发生演化。由于本身就比较小,上下盖层的渗透率演化可以忽略。绘制40年内热储层的渗透率k演化如图7,其他主要变量的演化见图8。从图7和图8可以看出,渗透率k与温度的等值线图形状比较相似,即在热开采过程中,渗透率k受温度的影响最大。以完全冷却区为界,区内渗透率高,区外渗透率低。但在流体入口和出口处,由于局部压力梯度大,孔隙压力对渗透率的影响也比较明显,表现为入口处渗透率高而出口处渗透率低。但总体来说,由于前0.01年域内孔隙压力迅速降低,导致渗透率普遍减小,因此渗透率在演化条件下时,其大小比给定的常数渗透率小。

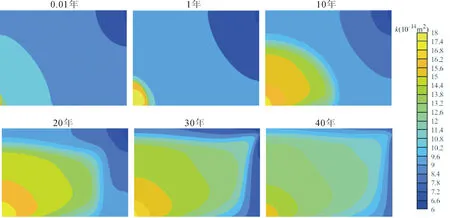
图7 EGS开采40年内热储层的渗透率k演化

考虑渗透率与否对传热性能指标的影响见图9。如图9(a),考虑渗透率演化时,出口水温的开始冷却时间提前1年左右。渗透率演化加快了出口平均温度的冷却速度。如图9(b),进入稳定开采阶段后,考虑渗透率演化时模拟所得的净热提取率比不考虑时提高了24.82%。

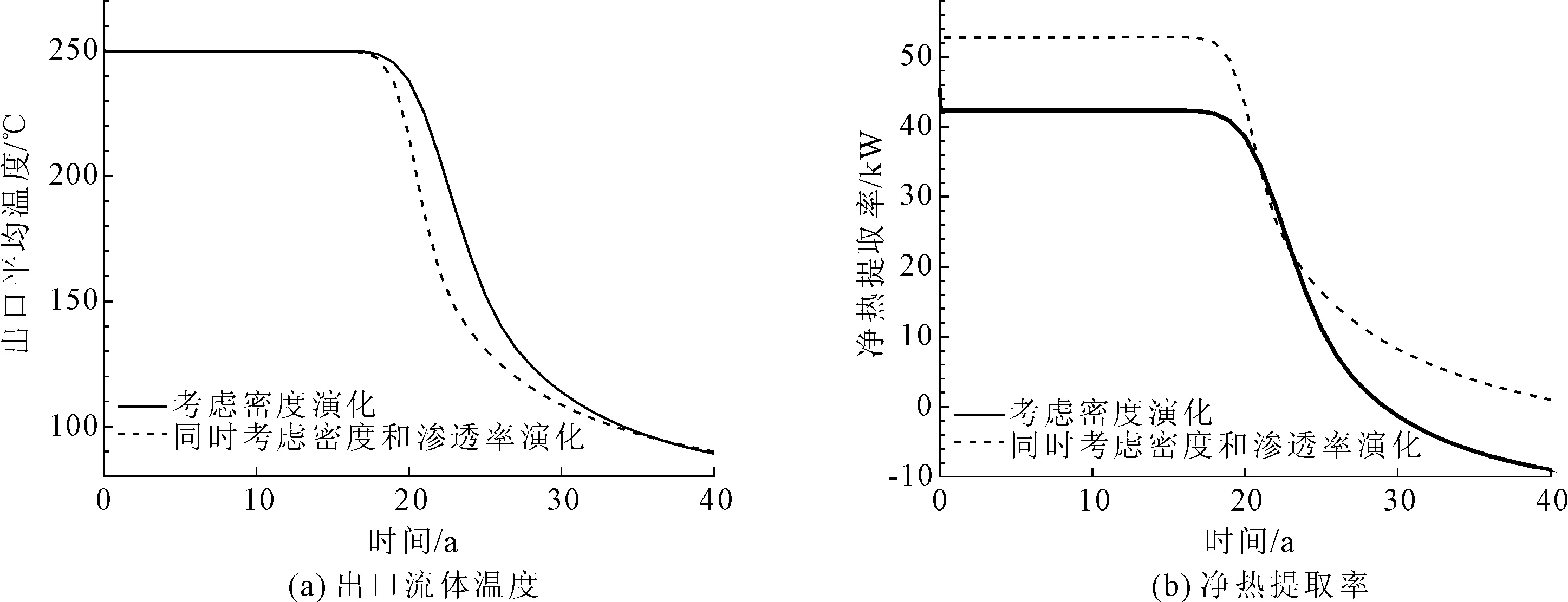
图9 考虑渗透率演化与否对传热效能的影响

3 结 论

(1) 随着EGS开采的进行,THM主要变量的演化如下:地层发生沉降,注入井和生产井的沉降量通常比其他区域多;孔隙压力的演化相比其他变量较快达到稳定,除了进出口处孔隙压力等值线稍微扭曲外,孔隙压力在空间分布上基本表现为沿竖直方向由下到上递减;温度分布体现了对流占优型问题的明显特点,即存在完全冷却区且完全冷却区逐渐向出口扩张。

(2) 考虑流体密度演化时,温度对流体密度演化的影响比孔隙压力的影响更大。在对比考虑流体密度演化与否对系统平均出口温度和净热提取率的影响时发现,考虑流体密度演化比不考虑时储层出口温度的开始冷却时间差别不大,但延缓了出口温度的冷却速度,而净热提取率比不考虑流体密度演化时提高约4.09%。

(3) 考虑流体密度和渗透率耦合演化时,温度对渗透率演化的影响比孔隙压力、围压等其他因素大。在对比考虑渗透率演化与否对系统平均出口温度和净热提取率的影响时发现,考虑渗透率演化时出口水温的开始冷却时间提前1年左右,加速了出口温度的冷却,而净热提取率比不考虑渗透率演化时提高约24.82%。