双向数据增强图卷积网络

郭新超，张维玉，夏忠秀

(齐鲁工业大学(山东省科学院) 计算机科学与技术学院，山东 济南 250300)

0 引 言

随着卷积神经网络的发展，一些学者提出了图卷积网络[1，2](GCN)。GCN的发展促进了图分析在现实世界任务中的应用，例如节点分类[3，4]、图分类[5，6]、链接预测[7-9]和社区检测[10]等。数据增强已被普遍用于提高机器学习模型的泛化能力，基于图数据的增强仍然是一个具有挑战性的问题，因为图数据比传统的数据更复杂，它由两个具有不同属性的特征组成：图拓扑结构和节点属性。

文献[11，12]提出了增加或消除边缘的不同策略，以提高GCN的健壮性。然而，这些增强方法仅限于修改图中具有特征的节点的一部分，增加了用于训练的数据量，但是这些修改可能会引入许多噪声或者删除了关键特征。在文献[13]中提出了节点并行的数据增强方法，为不同的节点建立互不相同的增强空间，但是这种方法摒弃标签传播的特性，在标签数据不足的情况下效果较差。

因此本文在改进自适应多通道图卷积网络模型[14]的基础上提出了双向数据增强图卷积网络(TDA-GCN)，在增强的过程中有效的对关键信息进行保护，通过一个图熵系统计算图中的信息量，在子图熵改变最小情况下为区域内的每一个节点设计一个独立的增强过程，通过两个卷积模块来提取相应的嵌入，然后用注意力机制来自动学习不同嵌入的权重，对它们进行自适应的融合，提高了模型的分类精确度。

1 相关工作

1.1 数据增强

数据增强在训练深度学习模型中扮演着重要的角色，它只对输入数据进行操作，而不改变模型结构，但显著提高了性能。现有的数据增强的方法中，如文献[11]是基于节点采样的方法，它通过随机删除部分节点以及与丢弃节点相连的边来对子图进行小批量训练；文献[12]的作用类似于一个数据增强器，它以一定的比率从输入图中随机删除边，形式上，它随机强制邻接矩阵A的一定比率的非零元素为零，从而生成子图；文献[15]增加二维形状数据使用，标准的现成的卷积神经网络模型训练与新颖的数据增强技术结合取得了显著的效果；文献[16]是一种基于图特征矩阵的扰动方法，它将某些节点的特征设为零向量；文献[17]利用迁移学习，使用大规模数据集上的训练模型的参数来训练小规模的数据集，可以作为一种特殊的数据增强方法。上述方法虽然达到了增强效果，但是没有一个相应的评判标准来衡量这种改变边或节点的增强方法是否改变了关键信息。

1.2 标签传播

半监督节点分类起源基于图的半监督学习，它通过探索图的结构，充分利用有限的标签数量，用已标记节点的标签信息去预测未标记节点的标签信息。通过节点之间的边传播标签，边上的权重越大，证明两个节点越相似，所以标签更容易进行传播。因此，它们可以表示为最小化目标函数

φ(Y)=12∑i，jωij(yi-yj)2

(1)

式中：ωij是节点vi和vj之间的相似性。

但是，大多数基于图的半监督学习算法忽略了网络拓扑或节点特征。当节点特性被忽略时，像标签传播这样的方法只利用网络上的标签传播(拓扑信息)，即ωij=aij， 这是邻接矩阵中的一个元素。其它方法在相似图中传播标签，该相似图是在没有考虑拓扑信息的情况下由节点特征构造的。在相似图中，ωij=exp(xi-xj22/σ2) 是使用它们的特征计算顶点vi和vj之间的相似性。图中标签的传播过程可以看作是用给定的标记细化图的结构。

1.3 图卷积网络(GCN)

图神经网络中的核心操作是邻域传播，信息通过某些确定性传播规则从每个节点传播到其邻域。例如，GCN采用传播规则X(l)=σ(AX(l-1)W(l))， 式中X(l)∈n×d(l)和X(l-1)∈n×d(l-1)是l层的输出和输入的节点表示矩阵，A^=- 12A^- 12，是对角节点度矩阵，式中=A+I是添加了自连接的邻接矩阵，W(l)∈d(l-1)×d(l)是特定层的可训练权重矩阵，σ是非线性激活函数，如ReLU。文献[18]对近年来卷积神经网络的发展进行了一个系统的概述，GCN通过传播邻居的表示并在此之后进行非线性变换来学习每个节点的表示。GCN最初应用于半监督分类，式中只有部分节点在图中具有训练标签。通过传播过程，标记节点的表示携带来自其通常未标记的邻居的信息，因此训练信号可以传播到未标记的节点。图卷积网络的结构如图1所示。

图1 图卷积神经网络模型结构

2 方 法

2.1 概 述

本文提出的TDA-GCN方法的模型框架图如图2所示，主要分为4个步骤：①将图分为节点特征图和拓扑结构图，其中节点特征图由节点属性的k近邻图生成；②在节点特征图和拓扑结构图上用改进的k-means算法选取一个子图区域，根据区域内图熵的变化，对节点特征图和拓扑结构图进行增强；③然后将增强后的图与原来的图共同作为输入，通过卷积神经网络提取不同的嵌入；④提取出的嵌入通过注意力机制进行自适应融合，得到最终的嵌入表示。

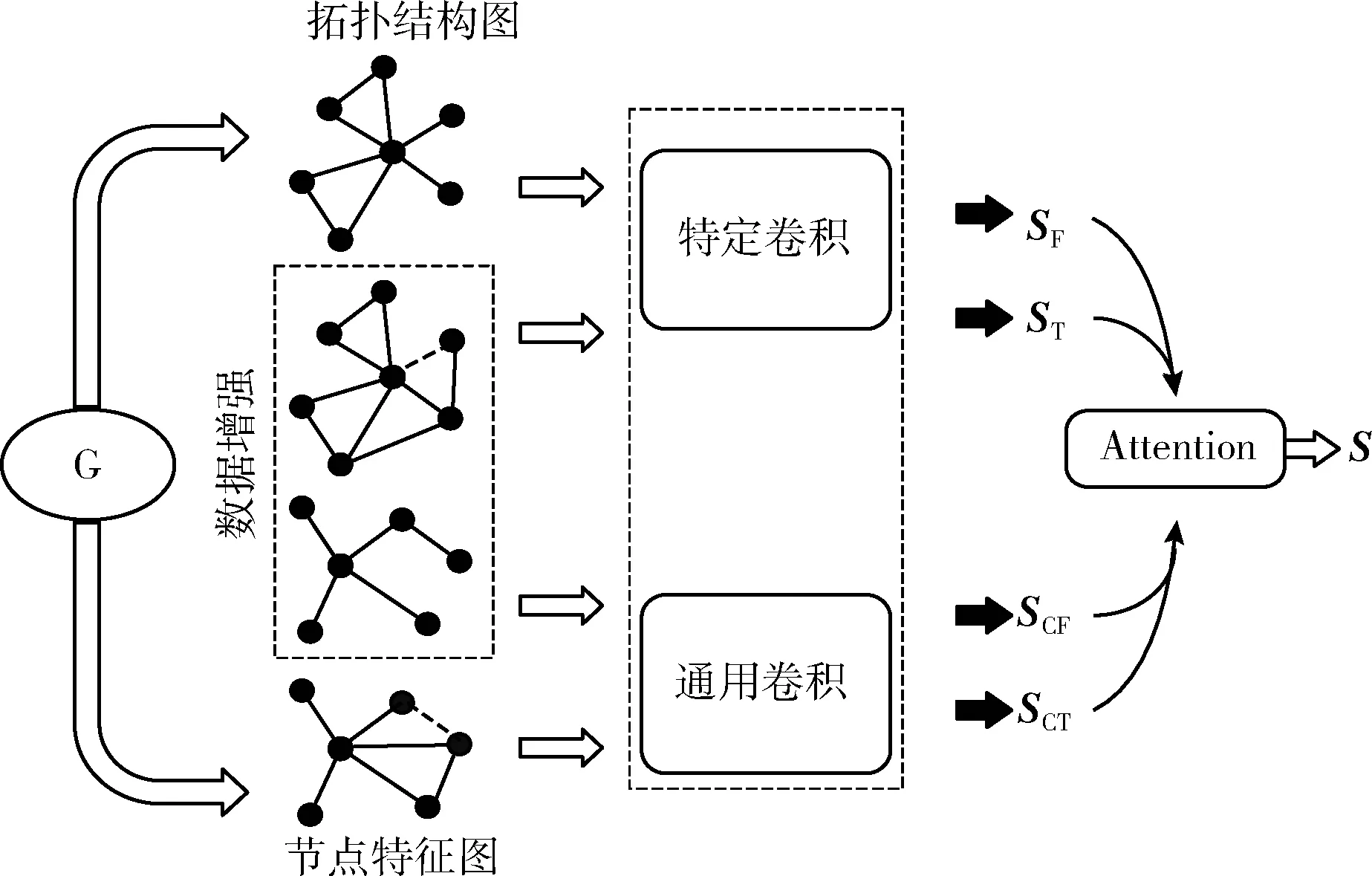
图2 TDA-GCN模型框架

在本文的方法中，图G=(A，X)， 式中A∈Rn×n是具有n个节点的对称邻接矩阵，X∈Rn×n是节点特征矩阵。具体来说，当节点i和j之间存在一条边时，Aij=1， 否则，Aij=0， 假设图中的每一个节点属于一个C类。

2.2 基于图熵的数据增强

与图像数据增强[19]不同，图形数据的非欧几里得结构导致图像数据的增强方法不能使用在图形数据上。本文设计了一种数据增强模式，首先对图中的节点进行聚类处理，把图划分为许多不同的子图，具体方法是使用Canopy聚类算法对图上的节点进行一个“粗”聚类，将相似的节点归纳进一个子图中，经过计算得到若干子图，各个子图之间可以是重叠的，但不会存在某个对象不属于任何子图的情况，得到子图的个数k和初始的聚类中心，并根据图中节点数量去调整k值和聚类中心，然后再使用k-means对子图进一步“细”聚类，把子图的划分标准更加细化，可以把这一阶段看作数据增强的预处理。然后对子图进行随机的删除或者增添边，每次删除或添加之前都选中一个节点，然后对其添加边或者删除相邻边，如图3所示，如果是只有一条边的节点则不删除边，即保证删除边后的图仍为连通图，得到的子图称为副子图，然后用式(2)来分别计算该节点删除边后和添加边后的副子图的图熵，用该子图初始的图熵作为评判标准，从副子图中分别选取图熵变化最小的副子图来作为该子图的增强子图，然后作为一个增强后的图

H1(X)=-∑|X|i=1p(xi)logp(xi)

(2)

式中：X是离散系统，-logp(xi) 表示xi∈X的发生概率p(xi) 的自信息，子图的熵由H1(X) 定义。

为了从副子图中筛选出想要的子图，使用图熵作为评定标准，但是这只体现在子图上，也就是说是局部最优。用式(2)分别计算图上的图熵和增强后的图的图熵，以无增强的图熵作为初始值，然后依次选择副子图熵变化最小的增强图，计算它的图熵，如式(3)

H2(X)=θH′(X)+(1-θ)H″(X)

(3)

式中：H′(X) 是增强后副子图的熵，H″(X) 是增强后图的熵，θ表示权重，以最小图熵的增强图作为一个输入。这样就得到了局部最优、全局最优的增强图，它们共同作为数据增强的结果图来作为输入，用图卷积网络进行提取嵌入表示。

2.3 卷积区域

2.3.1 特定卷积

现有的多数的图卷积操作遵循邻域聚合(或消息传递)方式，通过传播其邻居的表示并在此之后应用转换来学习节点表示。一般图的第l层卷积可以描述为

a(l)i=PROPAGATION({x(l-1)i，{x(l-1)j|j∈Ni}})

(4)

x(l)i=TRANSFORMATION(l)(a(l)i)

(5)

式中：x(l)i为节点i在第l层的表示，x(0)i初始化为节点特征xi。 GCN[6]、GIN[20]、GAT[21]等大多数图卷积都可以在该框架下通过不同的传播和转换机制得到。

为了提取节点特征图里节点的信息，使用节点的特征矩阵X构建了一个k近邻图(kNN图)Gf=(Af，X)， 式中Af是kNN图的邻接矩阵。具体来说，首先计算n个节点之间的相似矩阵M∈Rn×n， 选择使用余弦相似度获得的相似度矩阵M，然后为每个节点选择前k个相似节点用来设置边，最后得到邻接矩阵Af。 式中xi和xj是节点i和j的特征向量：

余弦相似度

Mij=xi·xj|xi||xj|

(6)

然后，利用特征结构中的输入图 (Af，X)， 第l层输出S(l)f可以表示为

S(l)f=ReLU(- 12ff- 12fS(l-1)fW(l)f)

(7)

式中：W(l)f是GCN第l层的权重矩阵，ReLU是激活函数，初始S(0)f=X，f=Af+If，f是f的对角矩阵，SF是最后一层输出的嵌入表示。通过以上操作，就可以学习节点嵌入，它在特征结构中捕捉特定信息SF。

对于拓扑结构信息，有原始的输入图Gt=(At，Xt)， 式中At=A和Xt=X。 使用与相同的计算方式在拓扑结构上学习嵌入ST， 这样，就在节点特征图和拓扑结构图上提取出特定信息。

2.3.2 通用卷积

特征结构信息和拓扑结构信息具有一定的相关性，节点分类任务可能与特征结构信息或拓扑结构信息以及它们的组合信息相关联。现在已经提取了特定嵌入，还需提取相应的共同嵌入，通过一个参数共享的通用GCN来提取节点特征图和拓扑结构图的共同嵌入。

利用拓扑结构输入图G(At，X)， 第l层输出S(l)ct可以用下所示

S(l)ct=ReLU(- 12ft- 12tS(l-1)ctW(l)c)

(8)

式中：W(l)c是第l层的权重矩阵，S(0)ct=X。 当利用通用卷积从特征图 (Af，X) 中学习节点嵌入时，为了提取共享信息，为通用卷积的每个层共享相同的权重矩阵W(l)c， 如下所示

S(l)cf=ReLU(- 12ff- 12fS(l-1)cfW(l)c)

(9)

式中：S(l)cf是l层输出嵌入，S(0)cf=X， 参数共享的权重矩阵可以从两个结构中筛选出共享特征。根据不同的输入图，可以得到两个输出嵌入SCT和SCF， 这两个结构的共同嵌入SC是

SC=λSCT+(1-λ)SCF

(10)

式中：SCT是通用卷积拓扑结构信息的嵌入表示，SCF是通用卷积特征结构信息的嵌入表示，λ参数表示权重。

2.4 注意力机制

通过以上的卷积操作，从节点特征图和拓扑结构图上提取出特定嵌入ST和SF以及共同的嵌入SC， 为了得到更精确的预测结果，通过注意力机制att来学习它们的重要性，相关的公式表示如下所示

(αt，αc，αf)=att(ST，SC，SF)

(11)

式中：(αt，αc，αf)∈n×1分别表示嵌入ST、SC、SF的n个节点的注意值。

对于变量i，ST的第i行的嵌入表示为SiT∈1×h， 首先对ST的第i行的嵌入进行非线性变换，然后通过激活函数与一个共享的注意向量q∈h′×1的转置得到最后的注意值ωiT如下

ωiT=qT·tanh(W·(SiT)+b)

(12)

式中：W∈h′×h是权重矩阵，b∈h′×1是偏差向量。同样地，可以使用式(12)获得SC和SF中节点i的注意值ωiC和ωiF。 然后，使用softmax函数对注意值ωiT，ωiC，ωiF进行归一化，以获得最终权重

αiT=softmax(ωiT)=exp(ωiT)exp(ωiT)+exp(ωiC)+exp(ωiF)

(13)

式(13)中较大的αiT意味着相应的嵌入更重要。同样求出αiC=softmax(ωiC)，αiF=softmax(ωiF) 的值。对训练集上的n个节点，通过式(13)已经得到权重αt=[αiT]，αc=[αiC]，αf=[αiF]∈n×1， 表示αT=diag(αT)，αC=diag(αC)，αF=diag(αF)。 把以上3种权重和嵌入结合，得到最终的嵌入S

S=αT·ST+αC·SC+αF·SF

(14)

2.5 目标函数

把式(14)中的输出嵌入S用于半监督分类，包括线性映射分类和柔性最大值激活函数分类。用Y^=[ic]∈n×C表示n个节点的类别预测，ic是节点i属于类别C的概率。然后Y^可以用以下方式计算

Y^=softmax(W·S+b)

(15)

式中：softmax(x)=exp(x)/∑Cc=1exp(xc) 就是所有类的规格化公式。

假设训练集是L，对于每个l∈L， 真实标签是Yl， 预测标签是Y^l。 在所有的训练集数据上，节点分类的交叉熵损失表示为ηt式中

ηt=-∑l∈L∑Ci=1YlilnY^li

(16)

结合式(2)、式(3)，确定最终的目标函数为

η=ηt+βH(X)

(17)

式中：β是图熵的超参数，H(X) 不同情况下分别表示H1(X) 或者H2(X)， 在标记数据的指导下，通过反向传播对模型进行优化，学习节点嵌入分类。

3 实 验

3.1 实验数据集

数据集的具体信息见表1。

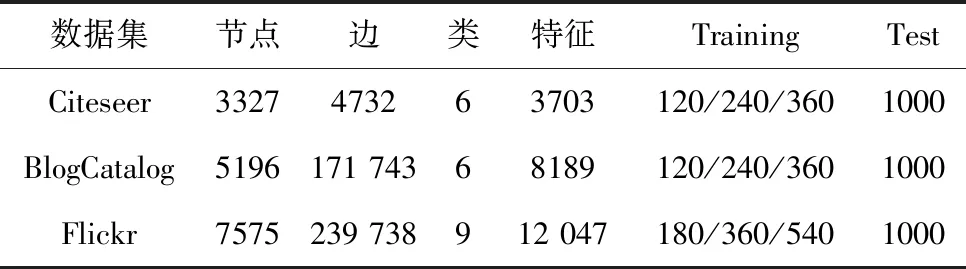
表1 数据集的统计数据

Citeseer：Citeseer是一个研究论文引用网络，节点是出版物，边是引用链接。节点属性是论文的单词包表示，所有节点分为6个区域。

BlogCatalog：它是一个社交网络，博主和他们的社交关系来自BlogCatalog网站。节点属性由用户档案的关键词构造，标签代表作者提供的主题类别，所有节点分为6类。

Flickr：Flickr是一个图片和视频托管网站，用户通过照片和视频的分享进行互动。它是一个节点代表用户，边代表其关系的社交网络，所有的节点按照用户的兴趣群体分为9类。

3.2 实验设置

操作系统：Ubuntu 16.04。软件版本：Python 3.7，Pytorch1.1.0，GPU：GTX 1080，CPU：inter Xeon E5-2679 v4@2.50GHz。使用每类20标签、40个标签、60个标签节点的训练集进行训练，使用10 000个节点用来进行测试，以获得鲁棒性更好的模型。这里的L/C是每个类的标记节点的数量，ACC是准确性，F1是F1宏观评分。表2中是本文模型具体的参数值。

表2 模型参数值

3.3 对比方法

将本文的方法与现有方法进行了比较，其中包含网络嵌入算法和基于图神经网络的方法。具体方法有以下：

GCN[2]是一个半监督图卷积网络模型，它通过聚集来自邻居的信息来学习节点表示。

kNN-GCN为了对比，用特征矩阵计算出的稀疏k-近邻图代替传统的拓扑图作为GCN的输入图，表示为kNN-GCN。

GAT[21]是一种利用注意机制聚集节点特征的图神经网络模型。

MixHop[22]是一种基于GCN的方法，它将高阶邻居的特征表示混合在一个图形卷积层中。

3.4 结果与分析

3.4.1 不同方法的实验结果对比

本文对比了不同模型节点分类精确度的结果，见表3、表4。表3列出了准确性下(ACC)的对比结果，表4列出了宏观评分(F1)下的对比结果。从图中可以看出，GCN在3个数据集上的分类精确度都不是最优，在Citeseer数据集上不如GAT，其余数据集上不如kNN-GCN，但是经过增强后的GCN在3个数据集上都有不同程度的提升，并且超过了上述模型，验证了数据增强方法的有效性。

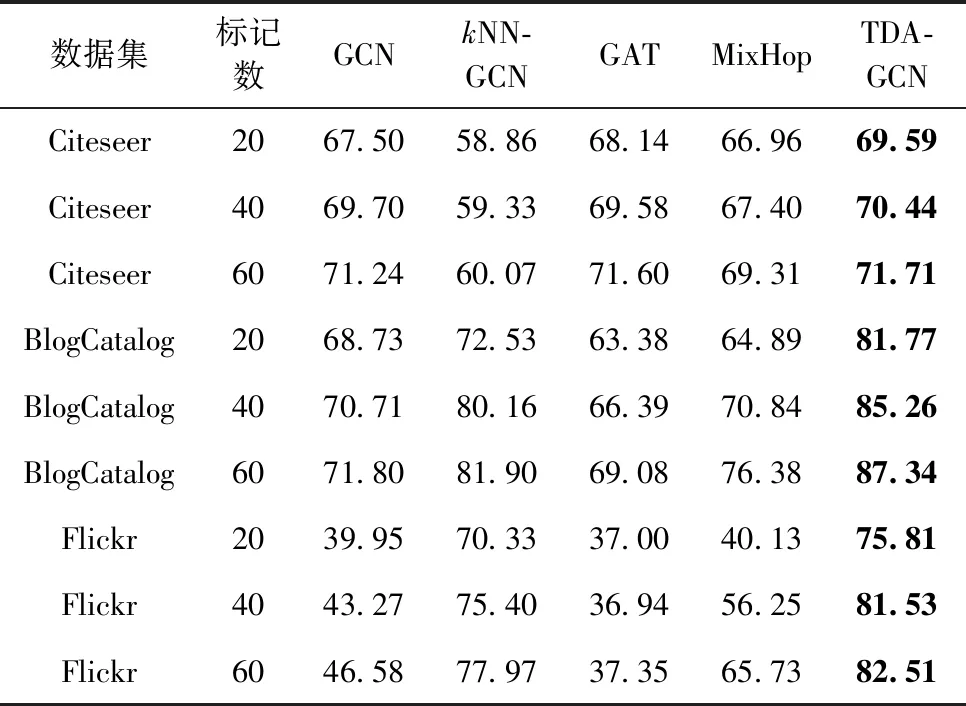
表3 实验结果(F1)

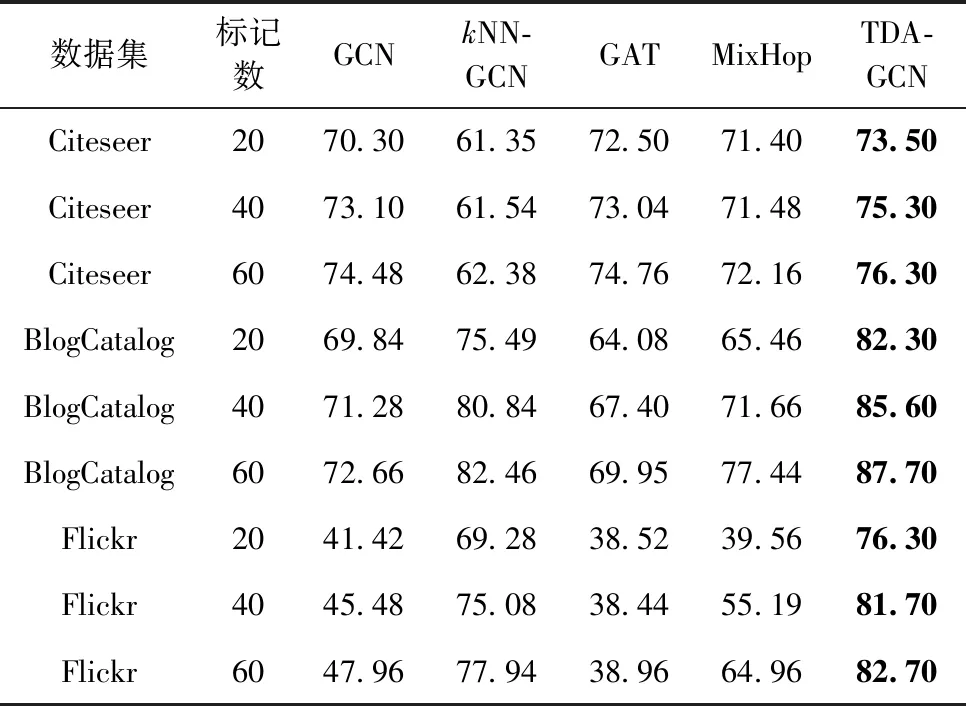
表4 实验结果(ACC)

TDA-GCN在最终结果上优于GCN和kNN-GCN，说明TDA-GCN可以从原始图中提取更多的有用信息，包括在拓扑结构和节点属性信息，并通过注意力机制对这些信息进行有效利用，也验证了注意力机制的有效性。

本文提出的TDA-GCN在所有的数据集中取得了最好的效果，准确性上，在BlogCatalog数据集上最大的提升效果达到了6.81%，在Flickr数据集上最大的提升效果达到了7.02%，在Citeseer数据集上提升了2.26%的效果，相比于对比方法，本文方法的提升效果较为明显，也验证了本文方法的有效性。

3.4.2 训练次数分析

在图4、图5展示了BlogCatalog与Citeseer数据集在不同数量标签下的迭代次数与分类精确度的训练曲线图，在前15次的迭代训练中，所有曲线有一个快速的增长，随着训练次数的增加，所有曲线都趋于平稳，但是增强后的模型在整体上占有优势。20标签的曲线在3条增强曲线中处于最低的水平，并与其它两条曲线相差较大，这说明了标签数量对分类精确度的影响。但是，分析发现40标签和60标签曲线相差较小，这说明随着训练次数和标签数量的增加，标签数量的对结果的影响在缩小。

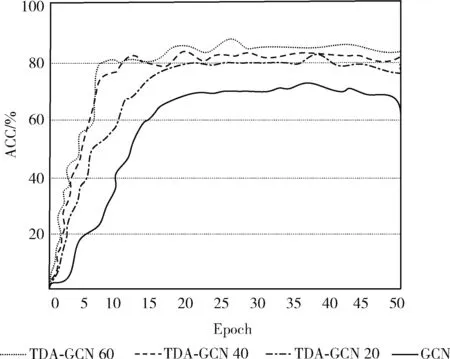
图4 BlogCatalog数据集的训练曲线

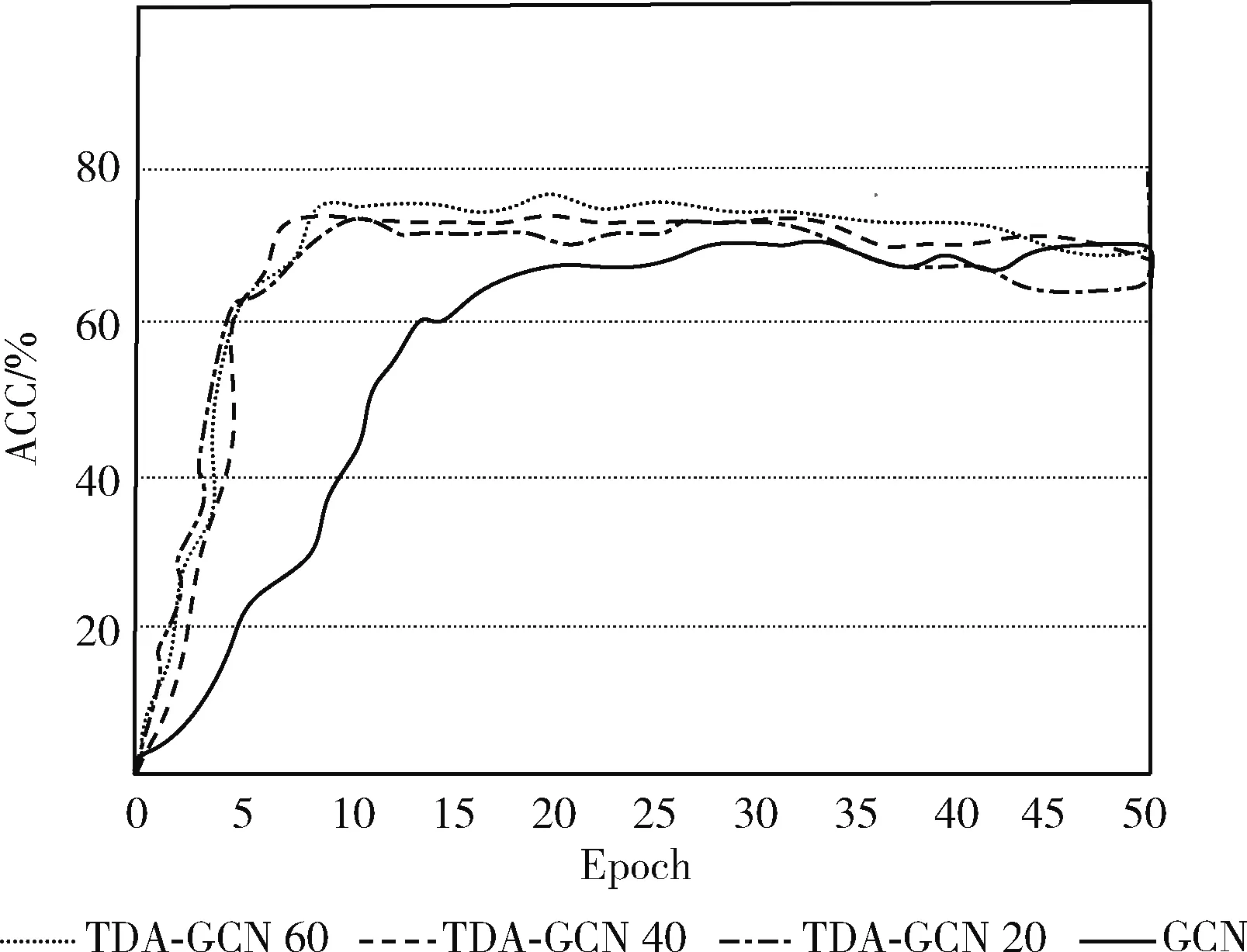
图5 Citeseer数据集的训练曲线

3.4.3 TDA-GCN与其变体对比分析

如图6所示，在这部分比较了TDA-GCN与其变体在3个数据集上的表现，以验证增强方法的有效性。

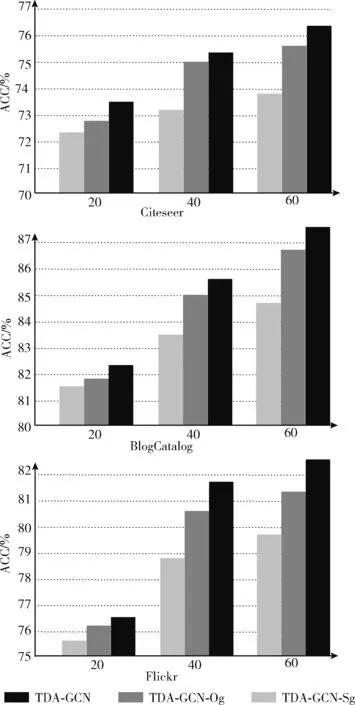
图6 TDA-GCN与其变体在3个数据集上的结果

(1)TDA-GCN-Og：只用全局最优的增强图；

(2)TDA-GCN-Sg：只用局部最优的增强图。

从图中的结果可以得出：在所有的数据集上，①TDA-GCN-Sg在所有数据集的增强效果不如TDA-GCN-Og，说明局部最优的增强效果过于单一，局部最优增强图在图中的权重占比较小；②TDA-GCN优于TDA-GCN-Og，但是差距不大，说明全局最优的增强图已经接近最好的增强效果，在增强过程中全局最优增强占比较大；③TDA-GCN-Sg在所有数据集上优于GCN，说明了本文增强方法的有效性。

4 结束语

本文针对数据不足带来的深度学习模型泛化性能较差问题，提出了双向数据增强图卷积网络(TDA-GCN)，通过子图增强法以及图熵选取的子图进行数据增强，不仅提取图的节点属性信息，而且也考虑拓扑结构上的信息，分别提取相应的嵌入表示，通过注意力机制融合生成最终的嵌入表示。这对训练出来的图卷积网络鲁棒性有一个显著的提升，在3个数据集也取得了最好的结果。未来我们的工作会致力于节点属性的数据增强，更好的节点属性会有助于最终的分类工作。