用于图像分类的模糊策略学习率ResNet

张睿权，覃 华

(广西大学 计算机与电子信息学院，广西 南宁 530004)

0 引 言

目前图像分类[1-6]主要用深度神经网络实现[7-11]，其中ResNet网络[12]具有网络层数较深时不容易出现梯度消失和爆炸的优点，但存在训练收敛难和过拟合等问题，这些不足与ResNet全连接层上的梯度训练算法有关。为此，出现了一些ResNet的改进训练算法。文献[13]用动态衰减率自适应梯度解决训练算法在某些应用场景中泛化能力下降的问题，文献[14]使用最大化过去平方梯度更新参数解决历史梯度对学习率的影响。文献[15]采用过去梯度的固定大小窗口来缩放梯度，改进了梯度算法的收敛性。文献[16]用混合幂和多维更新策略改进了梯度算法的收敛性。文献[17]提出的AdaBound算法通过学习率的上下界限实现了一种新的自适应梯度法，具有良好的训练收敛效果。受此上述文献启发，为改善ResNet的训练稳定性和收敛性，本文提出一种模糊策略的梯度下降法(fuzzy policy gradient descent，FPGD)用于ResNet全连接层的训练，核心思想是：首先把ResNet的训练看作一个无约束优化问题，推导出基于一阶梯度的神经元连接权重的迭代更新公式；接着设计一种模糊决策函数，用来自适应模糊调整权重更新公式的学习率。最后在经典的图像分类数据集CIFAR-100和CINIC-10上验证所提算法；与最新的AdaBound训练算法相比，所提算法在综合分类指标Kappa系数上分别提高了9.30%和9.27%，而准确率分别提高了9.16%和8.14%，宏召回率提高了9.16%和8.14%，宏精确率提高了8.09%和7.89%，宏F1提高了9.26%和8.17%。

1 ResNet深度神经网络的基本结构

ResNet深度神经网络的基本结构如图1所示，它是由一系列卷积层、残差模块和全连接层组成，其中Conv1、Conv2和Conv5等是由残差模块堆叠而成，其中残差模块是由卷积层串联在一起。图1中的上侧实线快捷连接是直接使用恒等快捷连接，有着恒等映射的作用；下侧虚线的快捷连接有两种选项：第一种是经过1×1的卷积核下采样，第二种是额外填充零输入以增加维度，不会引入额外的参数。全连接层是使用训练算法学习连接权重，最终产生输出。

图1 ResNet深度神经网络的结构

2 模糊学习率的梯度下降法

考虑一个无约束优化问题

minf(x)x∈Rn

(1)

其中，f是Rn→R上的连续可导函数，本文中此函数对应于深度神经网络的损失函数，而x是神经网络全连接层的连接权重。

解式(1)问题的一阶随机梯度迭代公式可写为

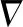
(2)

其中，αk>0是标量形式的学习率，k是迭代次数。f(xk) 是第k次的一阶随机梯度，xk是第k次的权重，xk+1是第k+1次的权重。传统的学习率αk通常是一个常数，不能根据实际迭代信息自适应地动态变化，从而影响了收敛速度和收敛效果，为此我们提出一种用二阶梯度信息设计的学习率，表示为

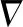
(3)

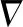
根据拟牛顿法的思想，令Dk=αkI，其中I为单位阵。矩阵Dk满足拟牛顿方程

Dksk-1=yk-1

(4)

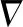
ak=minD=αID-1sk-1-yk-1

(5)

解式(5)的极小化问题，得

ak=sTk-1sk-1sTk-1yk-1

(6)

式(6)产生的学习率可能会过大或过小，导致算法迭代振荡，影响收敛的稳定性。为此，需要限制式(6)学习率的大小。本文提出了一种动态上下边界函数来控制式(6)的大小，方法如下。

αk的下边界ηk，l可定义为

ηk，l=-λe-k+λ

(7)

αk的上边界ηk，u定义为

ηk，u=(1-λ)e-k+λ

(8)

其中，λ是上下边界的控制因子，k为当前迭代次数。

在训练ResNet深度神经网络的过程中，由于图像数据集的数量较多，所以通常会随机选取多个图像样本组成一个小批量，然后用这个小批量来计算随机梯度。小批量的随机梯度定义如下

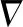
(9)

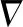
迭代次数k的取值范围是从0到K。T表示整个数据集分成多少个批次，t表示1到T每个批次间隔，那么可得到如下的权重序列 {xk，t}

{x0，1，x0，2，x0，3，…x0，T，k=0x1，1，x1，2，…x1，T，k=1…}

(10)

此时，使用历史信息修正的随机梯度写为

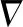
(11)

其中，xk，t表示第k次中t个批次的权重，mk，t表示第k次中t个批次的梯度，mk，t+1表示第k中次t+1个批次的梯度。mk，t+1是历史小批量梯度和当前小批量随机梯度加权平均。{βk}是在(0，1]范围内的序列，且该序列单调递减，用于控制历史小批量梯度对修正梯度的影响。那么，在两次迭代epoch之间，修正前后梯度之差为

yk=mk，T-mk-1，T

(12)

其中，yk是修正后第k次中T个批次的梯度和第k-1次小批量中T个批次的梯度之差。

更新前后权重之差为

sk=xk，T-xk-1，TT

(13)

其中，sk是第k次中T个批次的权重和第k-1次中T个批次的权重之差。

由式(12)、式(13)以及式(6)，可得

ak+1=sTksksTkyk

(14)

其中，ak+1是第k+1次的学习率。

由此，构造一个模糊决策函数clip()来解决学习率的过大、过小问题，实现学习率的自适应模糊计算，表示为

ηk+1=clip(ηk，l，αk+1，ηk，u)

(15)

其中，ηk+1是clip()输出的模糊学习率。clip()的工作原理是：如果ak+1<ηk，l， 则模糊学习率为ηk，l； 如果ak+1>ηk，u， 则模糊学习率为ηk，u； 其它情况，模糊学习率为ak+1。 由此可见，clip()函数实现了一组模糊策略，它能自适应地计算当前迭代学习率的大小，防止学习率过大或过小。

用模糊学习率ηk+1和修正后的随机梯度mk+1，t改写式(2)，得

xk+1，t+1=xk+1，t-ηk+1mk+1，t

(16)

式(16)就是本文所提模糊策略梯度下降法的迭代公式，可用于ResNet深度神经网络的训练。

3 FPGD训练的ResNet深度神经网络

3.1 用FPGD训练ResNet神经网络的流程

输入：图像数据集Yi={Y1，Y2，Y3，…，YM}， 其中M为图像样本的总数目。算法最大迭代次数为K。

输出：训练后的ResNet深度神经网络模型。

步骤1 算法参数初始化。设置初始学习率η、序列{βk}、上下边界的控制因子λ。迭代次数k=0。每个批次数据集的大小|β|。数据集的批次T初始化方法为：如果M%|β| 为零，T=M/|β|， 否则T=M/|β|+1。 批次变量t=1。

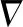
步骤3 如果t=1，那么mk，1历史小批量梯度提前设为零。用式(11)计算出修正的小批量梯度方向mk，t+1。

步骤4 如果k=1，模糊学习率直接取初值η。用式(16)更新小批量权重xk，t+1；

步骤5 如果t≤T， 迭代器t=t+1，转步骤2继续迭代。否则t重新设为1。

步骤6 计算出下一次迭代的模糊学习率：

(1)如果k=0，yk=mk，T， 否则用式(12)计算出在第k次和第k-1次中第T批次梯度之差yk；

(2)如果k=0，sk=xk，T， 否则用式(13)计算出在第k次和第k-1次中第T批次权重之差sk。

(3)用yk和sk结合式(14)计算出学习率ak+1。

(4)式(7)和式(8)计算出下边界ηk，l和上边界ηk，u。 调用式(15)计算出模糊学习率ηk+1。

(5)迭代计数k=k+1。转步骤2继续下一次迭代。

上述算法流程中的一些细节补充说明如下：

(1)步骤1中，λ<1。

(2)步骤1中，|β|的取值范围为[32，256]，通常设为2的若干次方。

3.2 FPGD的收敛性分析

采用统计标量R(K)[17]来判断FPGD的收敛性，其定义为

R(K)=∑Kk=1f(xk)-minx∑Kk=1f(x)

(17)

若K→∞时有R(K)/K→0， 此时可判断FPGD收敛。

本文引入文献[17]的两个假设来证明FPGD的收敛。

假设1：F⊂d为凸可行集。FPGD的训练权重xk∈F。 如果a-b∞≤D∞，a，b∈F， 那么D∞是F的边界直径。

由假设1和假设2可得到

R(K)≤D2∞K2(1-β0)∑di=1η-1K+D2∞K2(1-β0)∑Kk=0∑di=1βkη-1k+

(2K-1)R∞G21-β0

(18)

由式(18)可知，统计标量R(K)是有上界的。那么，当K→∞时，必然有R(K)/K→0， 因此FPGD是收敛的。

4 仿真实验

4.1 数据集和实验环境

CIFAR-100[18]图像数据集包括动物、植物、车辆、食品、家用家具和家用电器等20个大类共100个小类。每个小类有500张训练图像，100张测试图像，每张图像是32×32像素的彩色图像。数据集共计有50 000张训练图像，10 000个测试图像。

CINIC-10[19]数据集像包括动物交通工具等共计10个类别，共270 000张图像。

在PC机上实现算法和仿真实验，硬件环境为：CPU Intel i5-4590 3.3GHz，8GB内存；软件环境为Windows 10 64位，用Python 3.6和Pytorch 1.4实现算法。

4.2 实验参数设置与多分类评估指标

将FPGD与经典的深度学习梯度算法Momentum[20]、RMSProp[21]、Adam[22]、AMSGrad[14]和AdaBound[17]进行比较。采用ResNet-18作为深度神经网络模型，应用各训练算法对其进行训练。

各梯度下降算法的初始学习率统一设置为1e-3。FPGD的上、下边界控制因子λ=1e-3。所有梯度算法优化器的权重衰减参数设为5e-4。训练ResNet深度神经网络的批量大小为256。最大迭代次数取100次。

因数据集属于多分类问题，本文采用多分类指标评估各模型的图像分类效果，包括准确率(Accuracy，Acc)、宏精确率(macro-Precision，Pmarco)、宏召回率(macro-Recall，Rmarco)、宏F1值(macro-F1-score，Fmarco)以及Kappa系数[23]，它们的定义如下

Acc=NrecNall

(19)

Pmacro=1n∑ni=1Pi

(20)

Rmacro=1n∑ni=1Ri

(21)

Fmacro=2×Rmacro×PmacroRmacro+Pmacro

(22)

Kappa=p0-pe1-pe

(23)

其中，Nrec表示预测正确的样本数量，Nall表示总样本数量；n表示类别数。Pi表示类别i的精确率。Ri表示类别i召回率。p0是每一类别正确分类的样本数量之和除以总样本数，也就是总体分类精度；pe是所有类别分别对应的“实际与预测数量的乘积”的总和除以“测试集总数的平方”。

4.3 实验结果分析

4.3.1 CIFAR-100数据集上的结果

从表1中可看出，FPGD训练的ResNet-18，在CIFAR-100数据集上的5个评估指标值均优于相比较的其它梯度算法；其中综合指标Kappa系数值为0.7709，高于其它相比较算法。表1中Times是算法的计算时间，其中的h表示小时，m表示分，s表示秒。由表1可见，FPGD的耗时最少，但与其它算法差别不显著。用表1数据可计算出FPGD相对其它梯度下降算法在各指标上的变化百分率，结果如表2所示。在表2中，与最新的AdaBound相比，FPGD在Kappa指标上提高了9.30%，而准确率提高了9.16%，宏召回率提高了9.16%，宏精确率提高了8.09%，宏F1提高了9.26%。在综合分类性能指标Kappa系数上，FPGD比Momentum、RMSProp、Adam和AMSGrad分别提高了19.85%、14.70%、14.19%和12.36%，由此可见，本文算法对提高ResNet-18的分类效果是有效的。

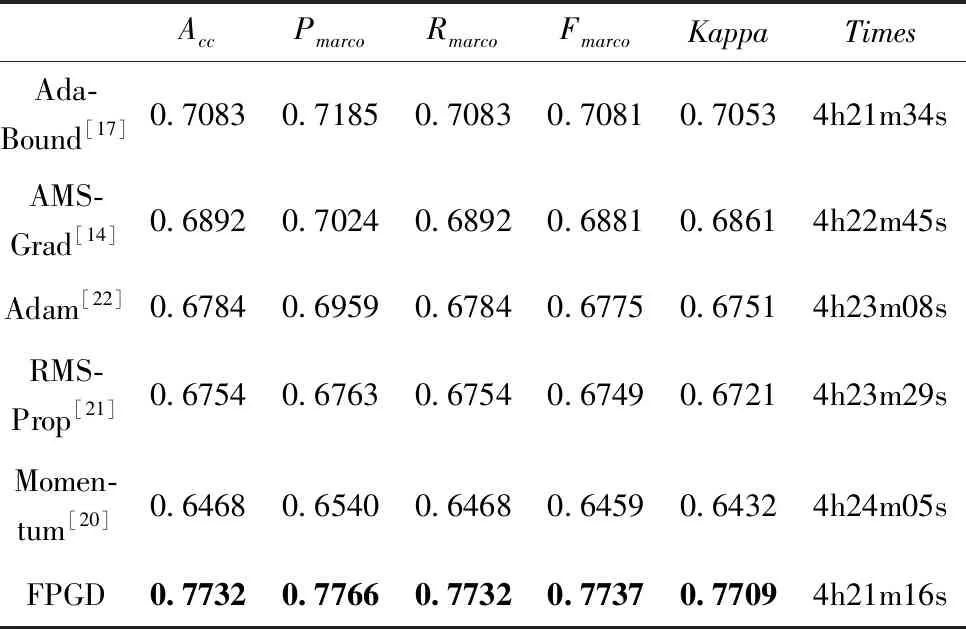
表1 在CIFAR-100上各算法的计算结果

表2 在CIFAR-100上FPGD较其它算法指标值提高的百分率/%

图2是各算法在迭代中损失函数值的变化趋势。由图2可以看出，FPGD只需要30次左右的迭代，损失函数值就开始趋于临界点并保持平直态势；相对之下，其它算法的损失函数值降低速度较慢，并且波动性大，例如AdBound和Momentum虽然接近FPGD的损失值，但两者需要迭代50次和90次左右，收敛速度显然慢于FPGD。AMSGrad、Adam和RMSPro在100次迭代中的最终损失函数值均大于FPGD。图2说明FPGP较其它算法具有更好的收敛性速度，从而验证了本文的模糊步长策略是有效的。

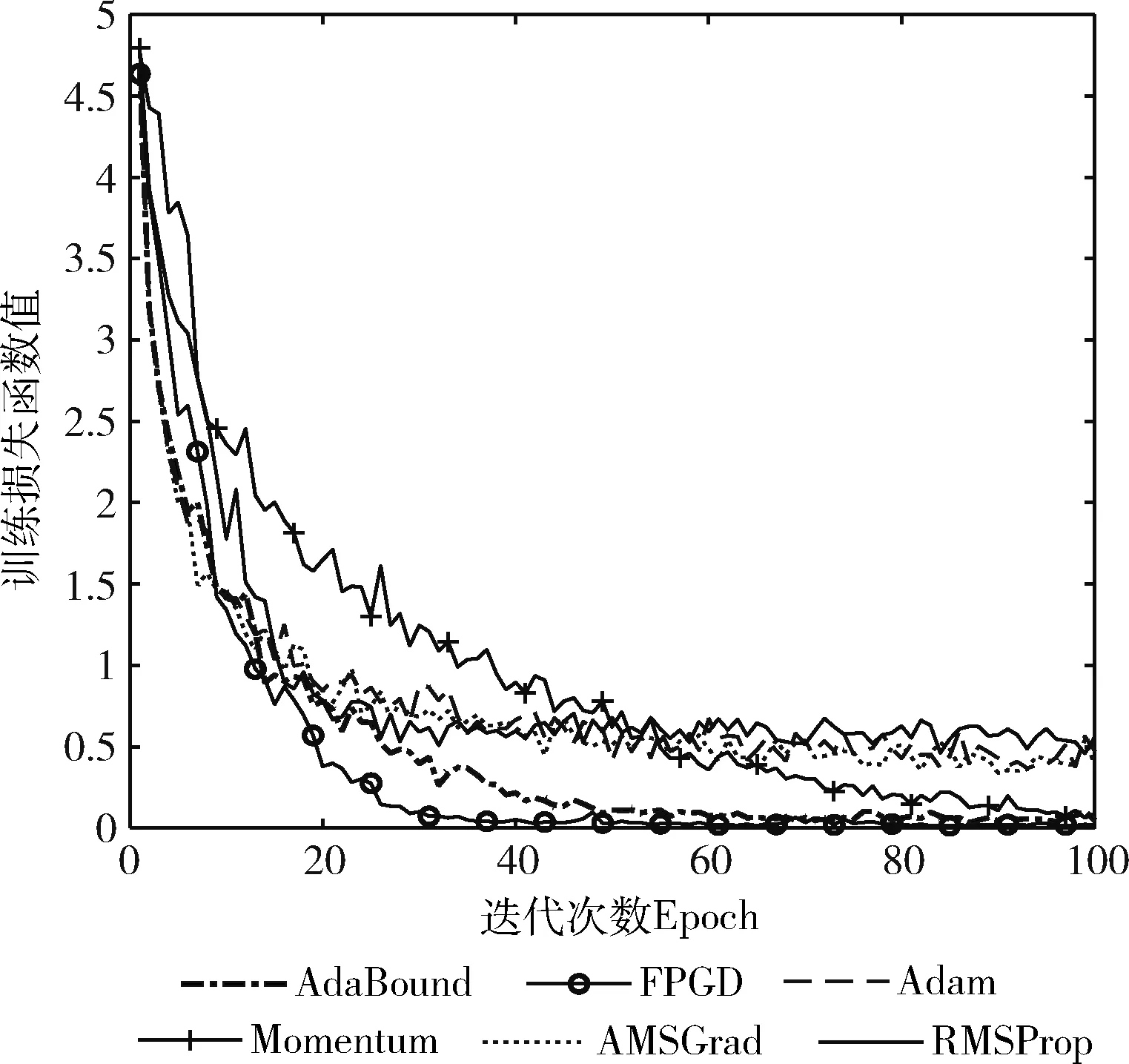
图2 CIFAR-100上各算法训练损失函数的变化

图3是各算法训练准确率变化趋势。由图3可看出，FPGD的训练准确率与AdaBound和Momentum相近，但收敛速度明显快于AdaBound和Momentum。AMSGrad、Adam和RMSProp虽然收敛速度与FPGD相近，但训练准确率都低于FPGD，这说明FPGD的寻优能力相对较强。

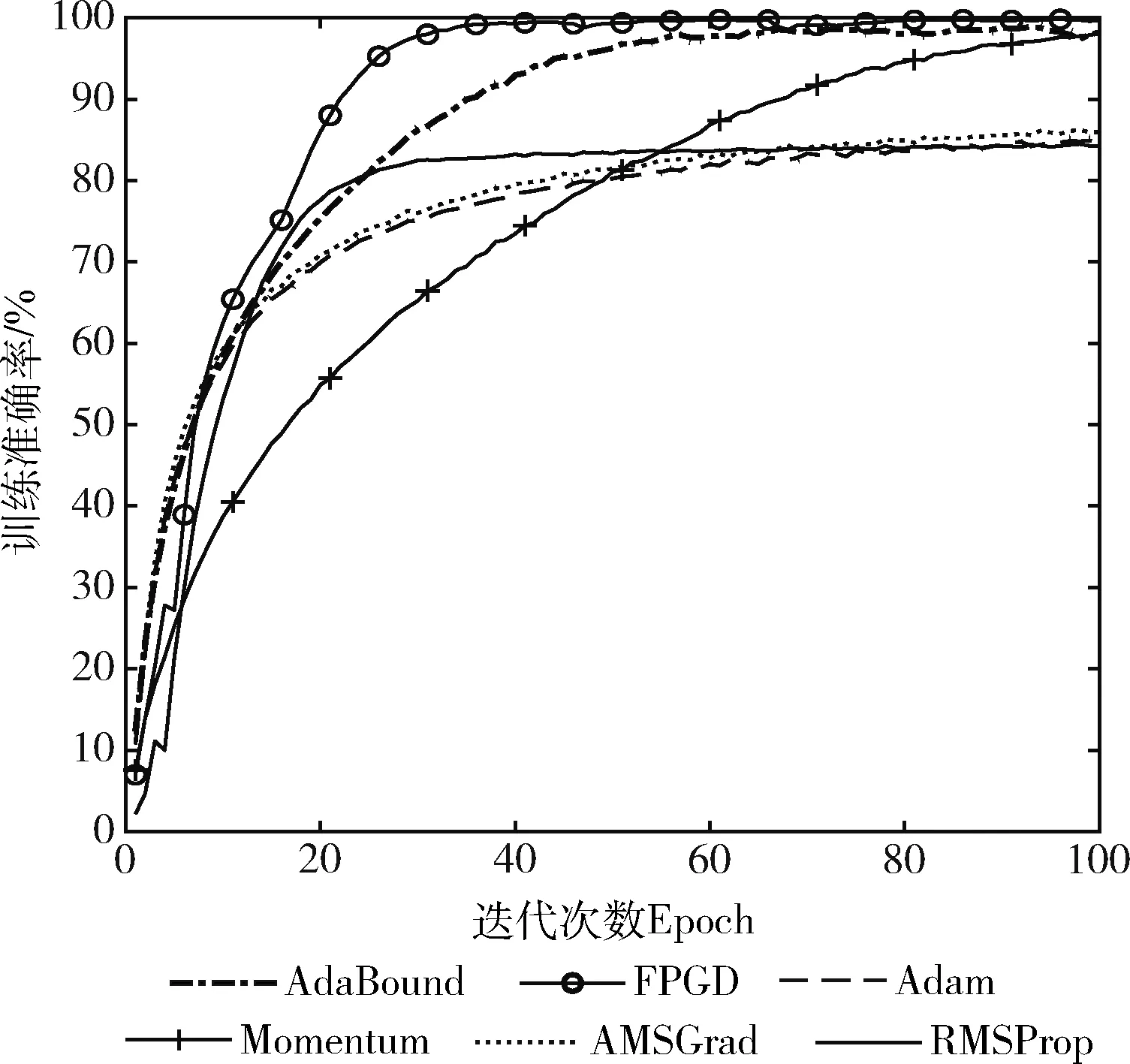
图3 CIFAR-100上各算法训练准确率的变化

图4是各算法的测试准确率。由图4可看出，FPGD的测试准确率优于其它算法。虽然FPGD的训练准确率与AdaBound和Momentum的最终训练准确率相近，但测试准确率高于AdaBound和Momentum，说明FPGD训练的ResNet-18模型的具有良好的预测能力，也验证了FPGD所获的连接层权重能更好地拟合数据集的特征，从而产生更好的测试准确率。

图4 CIFAR-100上各算法测试准确率的变化

4.3.2 CINIC-10数据集上的结果

表3是各算法训练的ResNet-18在CINIC-10数据集的指标值。从表3可看出，FPGD训练的ResNet-18，在CINIC-10数据集上的5个评估指标值均优于其它算法训练的ResNet-18模型。表3中Times是计算时间，其中h表示小时，m表示分，s表示秒。由表3可见，FPGD的耗时最少，但与其它算法差别也不显著。用表3数据可计算出FPGD相对其它梯度下降算法在各指标上的变化百分率，结果如表4所示。在表4中，与最新的AdaBound相比，FPGD在Kappa指标上提高了9.27%，而准确率提高了8.14%，宏召回率提高了8.14%，宏精确率提高了7.89%，宏F1提高了8.17%。在综合指标Kappa系数上，FPGD比Momentum、RMSProp、Adam和AMSGrad分别提高了12.62%、8.14%、10.01%和9.90%，由此可见，本文算法对提高ResNet-18的分类效果是有效的。

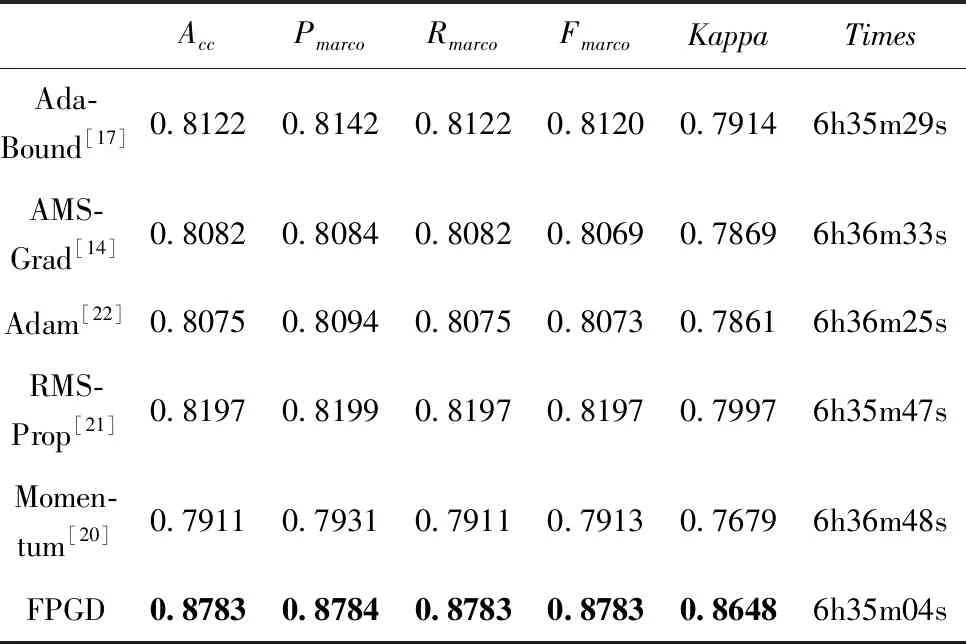
表3 在CINIC-10上各算法的计算结果

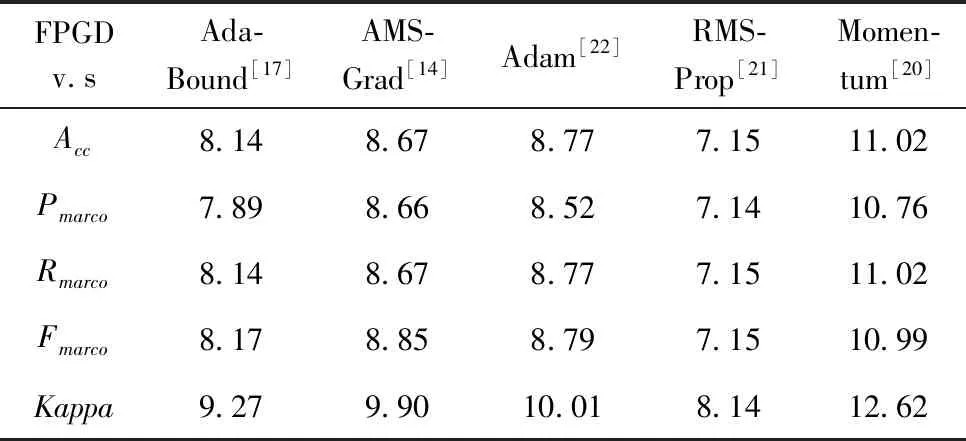
表4 CINIC-10上FPGD较其它算法指标值提高的百分率/%

图5是各算法在迭代中损失函数值的变化趋势。由图5可以看出，FPGD只需要40次左右的迭代，损失函数值就开始趋于临界点并保持平直态势；相对之下，其它算法的损失函数值降低速度较慢，并且波动性大，例如AdBound、RMSProp和Momentum虽然接近FPGD的损失值，但三者都迭代了60次左右才达到FPGD相同的效果。AMSGrad和Adam在100次迭代中的最终损失函数值均大于FPGD。图5说明FPGP较其它算法具有更好的收敛性速度和收敛稳定性，同时也验证了本文的模糊步长策略在有效的、可行的。

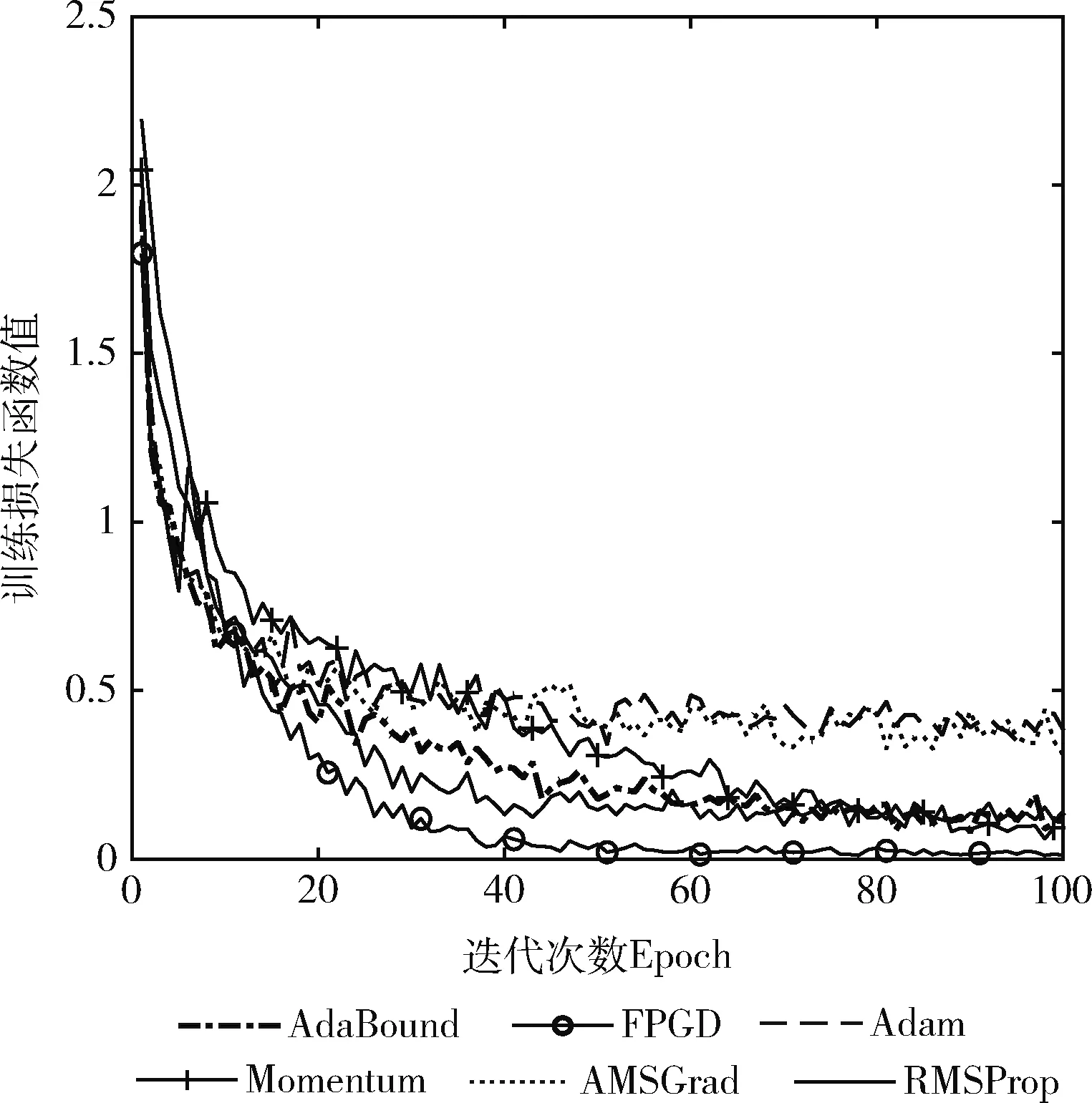
图5 CINIC-10上各算法训练损失函数的变化

图6是各算法训练准确率变化趋势图。由图6可看出，FPGD的训练准确率与AdaBound、Momentum和RMSProp相近，但收敛速度明显快于AdaBound、Momentum和RMSProp。AMSGrad和Adam虽然收敛速度与FPGD相近，但训练准确率都低于FPGD，这说明FPGD的寻优能力相对较强。

图6 CINIC-10上各算法训练准确率的变化

图7是各算法的测试准确率。由图7可看出，FPGD的测试准确率优于其它算法。虽然FPGD的训练准确率与AdaBound、Momentum和RMSProp的最终训练准确率相近，但其测试准确率高于AdaBound、Momentum和RMSProp，说明FPGD训练的ResNet-18具有良好的预测能力，也验证了FPGD所获的连接层权重能更好地拟合数据集的特征，从而产生更好的测试准确率。

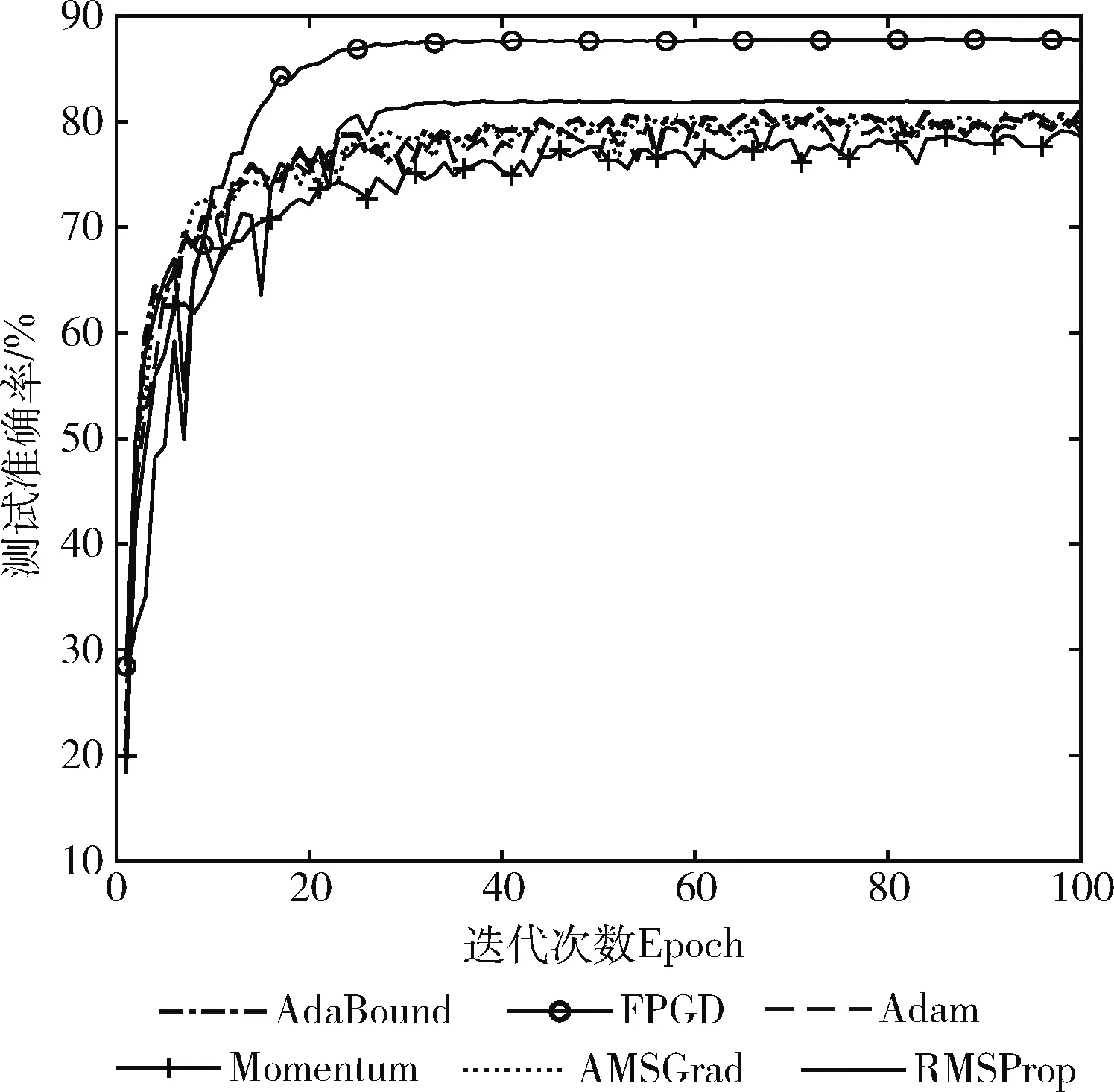
图7 CINIC-10上各算法测试准确率的变化

综合上述实验结果可看出，本文提出的模糊策略学习率梯度下降算法较相比较的其它梯度下降法具有更好的收敛性和稳定性，对全连接层权重的寻优能力更强，训练出的ResNet深度神经网络模型分类效果更好；特别是在综合性指标Kappa系数上，FPGD在两个数据集上的平均值较最新的AdaBound提高了9.28%，ResNet模型的改进效果是显著的。因此，本文所提的模糊策略学习率是有效的、可行的。

5 结束语

本文提出一种ResNet的模糊策略学习率梯度下降训练算法，具有良好收敛性，通过历史梯度和修正梯度计算出学习率，通过模糊策略限制学习率的大小，提高了训练算法的寻优能力和迭代稳定性。在CINC-10和CIFAR-100两个大型图像数据集上的实验结果显示，FPGP训练的ResNet各指标均优于相比较算法，因此，所提的模糊策略梯度下降训练算法是可行的和有效的。此外，虽然我们只在ResNet深度学习模型上验证FPGP的有效性，但FPGP设计上是通用的，对其它深度模型的全连接训练也同样适用，有较好的普适性。