高观点下探寻多边形的内角和与外角和

叶莹

三角形的内角和是一个重要的几何量，在欧几里得几何学中，三角形的内角和为180度.在证明这一定理的时候，中学教科书［1］采用的方法是这样的：首先过三角形的某一个顶点作与对边平行的辅助线，再利用内错角相等得到三角形的内角和为180度.而内错角相等需要利用欧几里得几何的两条公理：同位角相等和对顶角相等.由此可见，为了证明三角形的内角和为180度，需要两条公理.中学课本证明完三角形的内角和为180度以后，再利用内角和外角互补的关系，得到外角和为360度.

在讲完三角形的内角和与外角和以后，中学教材便开始讲凸多边形的内角和，课本中的讲法通常是这样的：从凸多边形的某个顶点出发，可以作（n－3）条对角线，从而把多边形分成了（n－2）个三角形，多边形的内角和正好是这（n－2）个三角形的内角和，因而是（n－2）×180°.相应地，因为每个顶点对应的外角和内角互补，所有内角和与外角和的总和是n×180°，从而外角和是2×180°=360°，详情可参考［1］.一般的教材也就到此为止，即得到凸n边性内角和公式为（n－2）×180°，外角和为360°.以上的证明过程无疑是正确的，然而笔者认为，许多很自然的问题还没有解决：1.如果是非凸多边形，它的内角和应该是多少，外角和应该是多少？ 2.为什么多边形的内角和与边数有关，而外角和与边数无关？3.证明多边形的内角和公式和外角和公式，有没有更加直观和更加简单的方法？笔者通过对这几个问题的长期思考，结合现代微分几何学的研究方法，认为多边形的外角和是比多边形的内角和更重要的几何量.如果换一种方式来讲解多边形的内角和与内角和，则不但讲解过程更加直观，而且不需要任何公理，此外，该讲解方法还适用于非凸多边形，最后，该讲解方法还可以很容易推广到现代微分几何学中的Gauss-Bonnet公式.下面笔者来详细叙述这种直观的讲解方法.

我们来观察一下三角形的制作过程.中学教科书中说，三条线段顺次首尾相接就构成一个三角形，实际上，我们只需要把一条线段折三次就能得到一个三角形，仔细观察折叠的过程，就能得到三角形的外角和为360度的结论.下面，我们来看看具体的折叠步骤：图2

首先，取一条线段（如图1）.

第一步：将AB段不动，BE段绕B点逆时针旋转α角度（如图2）.

第二步：将AB段、BC段不动，CE段绕C点逆时针旋转β角度，使得D、A、B三点在同一条直线上（如图3）.

第三步：将AB段、BC段、CD段都不动，DE段绕D点逆时针方向旋转γ角度，使得DE与AB共线（如图4）.

通过上述三步，一个三角形就形成了.巧合的是α、β、γ刚好是ΔABC的外角，那么它们的和是多少度呢？观察DE段，它在第一步逆时针旋转了α，第二步逆时针旋转了β，第三步逆时针旋转了γ，最终绕了一圈，回到了原来的方向，既然是绕了一圈，也就是说旋转了360°，即 α+β+γ=360°，也即三角形的外角和是360°，得到了三角形的外角和为360°以后，因为每个顶点处的内角与外角互补，所以内角和与外角和的总和是3×180°，因而得到内角和是180°.上述过程的实施非常简单，不需要教材中的辅助线等工具，并且这种方法可以推广到多边形，包括凸多边形和非凸多边形的情况.

先来看看凸n边形的内角和与外角和，将一条线段分成（n+1）段，用同样的方法，经过n步将线段绕不同的点旋转一定角度，就可以得到一个凸多边形（当然要求旋转的角度和线段的分段要适当），因此凸n边形的外角和360°，从而得到内角和是（n－2）×180°.

从上面的分析可以看出，无论是构造多少条边的凸多边形，其本质都是最后一段旋转了一圈，而每一次旋转的角度都是多边形的一个外角，因此凸n边形的外角和总是360°，这就是对多边形外角和的直观认识，这样理解外角和还有以下两个好处.

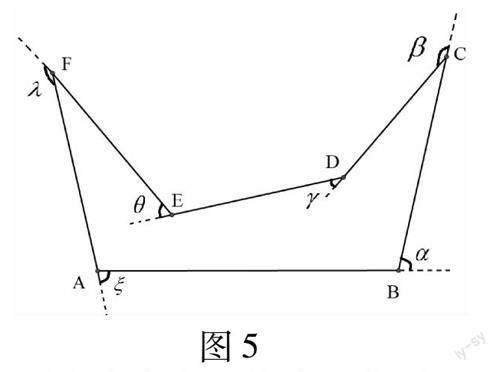
图5

第一是只要适当定义外角，上述结果也可用于非凸多边形的外角和与内角和.对于非凸的多边形，一般来说，不能通过在某个顶点处作对角线，而将多边形的内角和归结为三角形的内角和.如对于下面的非凸六边形（如图5），无论从哪个顶点出发，引对角线都无法将它切割成几个三角形，因而中学教材中的方法不适用于非凸多边形.但只要稍微调整我们的方法，就能得到非凸多边形的外角和和内角和公式，事实上，只需要注意旋转的方向是逆时针方向还是顺时针方向即可.我们以图5中的多边形为例，来看看具体的步骤.我们不妨规定逆时针方向为正方向，从而顺时针方向就为负方向.在第一步时，沿逆时针方向旋转了α度，记为+α.在第二步时，沿逆时针旋转了β度，记为+β.在第三步时，沿顺时针方向旋转了γ度，旋转的方向与前面相反，因而记为－γ.同理，第四步，因为是沿顺时针方向旋转了θ度，记为－θ.第五步和第六步是沿逆时针方向旋转，因此应为正向.观察整个过程，最后的结果是沿逆时针方向旋转了360度，因此有.一般的，對于任意的n边形，我们有外角和公式∑ni=1（－1）γiθi=360°，其中γi=1，  若第i个顶点处是逆时针方向旋转，

－1， 若第i个顶点处是顺时针方向旋转，  有了上面的外角和公式以后，再利用内角与外角互补的关系，我们也可以得到任意n边形的内角和是（n－2）×180°.

第二，该方法可以从离散情况推广到连续情况，甚至既有离散也有连续的情况.仔细分析刚才的过程，发现多边形的外角本身具有重要的几何意义，在每个顶点处，我们是把直线弯曲一定的角度，从而得到两条邻边，而这个弯曲的程度，就是这个顶点处外角的度数，换句话说，多边形的外角衡量的是直线在这一点的弯曲程度，在微积分和微分几何中，曲线的弯曲程度是用曲率来衡量的，既然外角和曲率都表示的是曲线（直线是特殊的曲线）的弯曲程度，因而它们具有同样的几何意义.将多边形的外角换成曲率，求和变成积分，就应该得到∮kds=2π.事实上，上述公式正是微分几何中的Gauss-Bonnet公式，详情可参考［2］.即在R2的一条光滑简单闭曲线上，曲率的曲线积分是2π，因此把多边形的外角理解为曲线的弯曲程度，可以方便地把初等几何学与现代微分几何学联系起来，当学生以后学习微分几何学时，可以很直观地理解曲率与Gauss-Bonnet公式.

在∮kds=2π中，我们要求曲线是光滑的、简单闭曲线，简单指的是曲线除了首尾相接以外，再无其它交点，光滑指的是曲线的方程在每一点可导.当然上述公式也推广到按段光滑的简单闭曲线，假设曲线由n段按段光滑的曲线Li（i=1，2，...，n）组成，其顶点为A1，...，An，顶点处的外角分别为α1，...，αn，则Gauss-Bonnet公式可表示为∑ni=1∫Likds+∑ni=1αi=2π.特别地，如果曲线的每一段都是直线，即k=0，则上式又回到了多边形的外角和等于2π这个简单的公式.

刚才讲到的Gauss-Bonnet公式针对的是平面曲线，其实Gauss-Bonnet公式还可以进一步推广到曲面上的曲线.假设区域D是曲面上按段光滑曲线L1，......，Ln所围成的区域，为简单起见，不妨假设D是单连通的，则曲面上的Gauss-Bonnet公式为∫DkdA+∑ni=1∫Likgds+∑ni=1αi=2π，其中k是曲面的Gauss曲率，kg是曲线的测地曲率，D是曲线所围成的区域.假定n=3，kg=0，即Li都是测地线（可简单地看成平面上的直线），则∫DkdA+π=∑3i=1（π－αi），右边是曲面上三角形的内角和.如果曲面就是平面（k=0），则上式就是中学教科书中的结论，即平面上的三角形的内角和等于180°.如果不是平面上的三角形，则其内角和通常不等于180°.当k>0时，内角和大于180°；当k<0时，内角和小于180°.例如，球面上的三角形，其内角和大于180°.而马鞍面上的三角形，其内角和小于180°.关于球面上的Gauss-Bonnet公式，详情可参考［3］［4］.

综上所述，在给中学生讲述多边形的内角和与外角和时，除了按照教科书中的讲法来讲之外，还可以从曲线弯曲的角度来先讲外角和，再根据外角与内角互补的关系，得到多边形的内角和公式.这样讲有几个好处.第一个好处是非常直观.不管是几边形，它都是一条线段经过若干次弯曲以后，绕了一圈，重新回到原来的方向所得到的图形.每一次弯曲对应多边形的一个外角，而绕一圈意味着多边形的外角之和为2π，再由外角与内角互补，得到内角和为nπ－2π=（n－2）π.第二个好处是，上述内角和公式与外角和公式不仅适用与凸多边形，也适用于非凸多边形.凸多边形的内角和可通过三角剖分得到，而非凸多边形的内角和不能通过三角剖分得到，因而上述方法将凸多边形的内角和公式推广到了任意多边形.第三个好处是将外角理解为曲线的弯曲，可以将多边形外角和公式推广到按段光滑封闭曲线的Gauss-Bonnet公式，使得学生在学习微分几何时，可以快速地理解Gauss-Bonnet公式的直观意义，从而发散学生的思维，供有余力的学生思考.第四个好处是可以让学生知道，除了欧几里得几何以外，還有非欧几里得几何.在非欧几里得几何中，三角形的外角和与曲面的Gauss曲率相关.

参考文献

［1］义务教育教科书《数学》八年级下册［M］. 北京师范大学出版社.

［2］彭家贵，陈卿.微分几何［M］，高等教育出版社.

［3］陈省身，陈维桓.微分几何讲义（第二版）［M］，北京大学出版社，2001.

［4］S.S.Chern， A simple intrinsic proof of the Gauss-Bonnet formula for closed Riemannian manifolds， Ann. of Math.，45（1944）， 747-752.