在解题教学中发展和完善学生的CPFS结构

周恩超

二、完善学生CPFS结构对问题解决具有重要意义

有了跟同学们的以上交流，不难理解学生思维受阻原因了，他们找不到解决问题的突破口，关键是学生的“CPFS”结构残缺、不完善导致.所谓“CPFS”结构即概念域、概念系、命题域、命题系形成的结构（概念域（concept field）、概念系（concept system），以及命题域（proposition field）、命题系（proposition system）.

在数学问题解决的过程中，如何将问题条件或結论用数学语言去作等价描述，即对问题如何进行“有意义的等价表征”，这是解题思路获得的前提和开端；其次要积极寻找当前问题的“迁移源”，进行模式识别、概括、类比的合理借鉴，而不是盲目地“试误”；再者，在解决问题的执行过程中，同样需要解题者自我监控，及时反思、调整.以上都需要解题者具备相关问题的概念域（系）和命题域（系），而个体形成了良好的CPFS结构，就是在长时记忆中贮存了与所要解决的问题相关的数学知识信息，知识间彼此相连，形成个性的、稳固的知识网络，新问题的解决的实质就是搜寻、提取、激活相关知识结点的过程.CPFS结构是数学所特有的认知结构，它不但包括数学的概念、公式、定理、公理等“硬件”，而且包括数学思想方法、数学观念等“软件”.其知识命题之间除了上、下位关系外，还包括“等价”这种同位关系，因而，知识结点的激活将更容易、更全面，解决问题的渠道更加畅通.试想，如果我们能在日常教学中，根据学生们的数学解题体验，帮助学生逐步建立、完善“CPFS结构”，那么对学生的解题该有多大帮助.

三、发展和完善学生CPFS结构的教学策略

1、在概念、命题教学中，加强数学理解形成网络体系

在概念、命题教学中，一定要重视知识产生、发展的过程，深刻认识数学对象的背景、产生途径和规则的逻辑依据，把握数学对象的本质，帮助学生建立关于以上观念的内部网络.只有学生了解了一个概念（或命题）与其他概念（或命题）的相互关系以及它们在优化后的认知结构中的位置，学生才能真正地视为己有，才能灵活地迁移应用.要引导学生学会从系统的观点整理概念和命题的方法，把有关概念和命题串成锁链、编成网络、配以图示、纵横联系，使学生主动获得一个个有序的概念组和命题组块，能从整体中看部分，从部分中看整体.

2、在解题教学中，通过反思、提炼数学体验完善认知结构

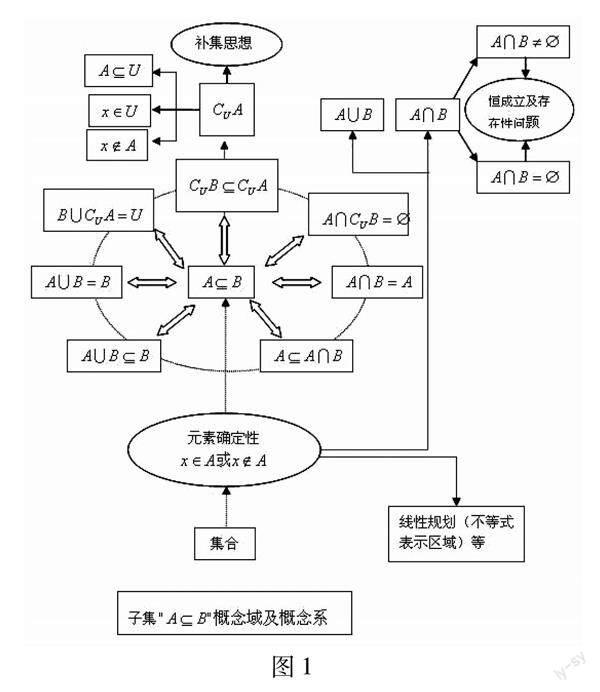
问题是数学的心脏，寻找和发现数学问题，是获得数学发现和进行数学思维的基本方法之一，同时，也是完善和发展个体“CPFS”结构的必经途径.在解题教学中，要重视学生的数学体验，引导学生在数学实践中反思、整理、归纳、提升，模式识别分类后进行有意义储存，达成“长时记忆效果”.在具体教学中，多采取“问题链”、“抛锚式”的教学策略，适当进行变式教学，一题多解、并多解选优.重视解题后的回顾与反思，培养学生“研究意识”，及时积累加工后的“雕虫小技”，让思考、积累成为一种习惯.在“理论、实践、再理论、再实践”的螺旋交互过程中，内化、补充、优化、完善已有的认知结构.例如在集合教学中通过以下题组训练：

（1）已知集合A=［1，2］，B={xx2－x－a≤0}，若AB，求实数a的取值范围？

（2）已知集合A=［1，2］，B={xx2－x－a≤0}，若A∩B=，求实数a的取值范围？

（3）已知集合A=［1，2］，B={xx2－x－a≤0}，若A∩B≠，求实数a的取值范围？

让学生深刻理解集合语言“AB、A∩B=、A∩B≠”的等价表征，将问题转化为“恒成立问题或存在性问题”解决，由此展开并结合学生原有的解题实践，帮助学生逐步建立完善以下认知结构：

3、重视元认知教学策略，提高学生自我监控能力

数学解题的认知结构是由解题知识结构、思维结构和解题的元认知结构所组成.因此加强学生数学元认知能力的培养，有利于训练学生解决问题的“自醒意识”，避免走弯路或少走弯路，并能做好及时调节.一旦这种“自我监控能力”得到提高，就会从根本上改善学生的学习方式，学生个体“CPFS结构”的生成建构，便会由点到线、由线到面.同时，也会随着学生数学认识的提高和对数学实践的反思，对已有的“CPFS结构”进行动态调整、完善.所以，帮助学生提高元认知知识，丰富学生的元认知体验，指导学生调节与监控自己的学习过程，是教师日常教学中不应忽视的重要任务.发展和完善学生的“CPFS结构”对学生的数学学习意义重大，对老师的教学提出更高的要求和挑战.对此，我们应不懈努力.

参考文献

［1］喻平.数学学习心理的CPFS结构理论与实践［M］．南宁：广西教育出版社，2008．4.

［2］喻平.数学教学心理学［M］．北京：北京师范大学出版社，2010．2.

［3］沈文选，杨清桃．数学思想领悟［M］．哈尔滨：哈尔滨工业大学出版社，2008．1.