一道联考测试题的探究与拓展

连其秀

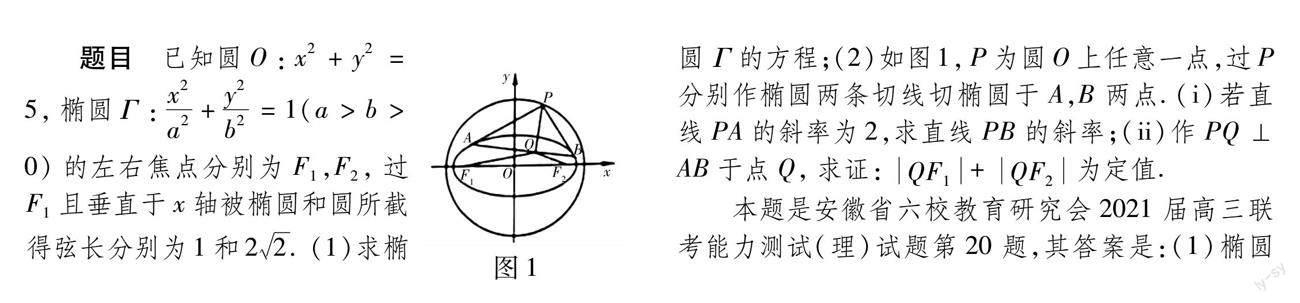
题目 已知圆O：x2+y2=5，椭圆Γ：x2a2+y2b2=1（a>b>0）的左右焦点分别为F1，F2，过F1且垂直于x轴被椭圆和圆所截得弦长分别为1和22.（1）求椭圆Γ的方程；（2）如图1，P为圆O上任意一点，过P分别作椭圆两条切线切椭圆于A，B两点.（i）若直线PA的斜率为2，求直线PB的斜率；（ii）作PQ⊥AB于点Q，求证：QF1+QF2为定值.

本题是安徽省六校教育研究会2021届高三联考能力测试（理）试题第20题，其答案是：（1）椭圆Γ的方程为x24+y2=1；（2）（i）直线PB的斜率为－12；（ii）QF+QF2为定值85.其中破解（2）的（i）、（ii）的关键步骤分别是求得直線PA，PB的斜率之积k1k2=－1，及点Q的轨迹为与椭圆Γ有公共焦点的椭圆5x216+5y2=1.观察圆O：x2+y2=5和椭圆Γ：x24+y2=1，发现5=4+1.

我们不禁要问：对于一般的圆O：x2+y2=a2+b2和椭圆Γ：x2a2+y2b2=1（a>b>0），直线PA，PB的斜率之积k1k2=？点Q的轨迹是否为与椭圆Γ有公共焦点的椭圆？