基于长期气温模拟的混凝土坝变形预测混合模型
2023-09-12陈旭东侯阵阵郭进军
陈旭东,侯阵阵,郭进军,2
(1.郑州大学黄河实验室,河南郑州 450001; 2.南京水利科学研究院,江苏南京 210017; 3.国家大坝安全工程技术研究中心,湖北武汉 430010)
我国是一个大坝工程建设大国,截至2019 年年底,共修建各类水库大坝9.8 万余座。 水库大坝在发电、防洪、供水等方面发挥巨大作用的同时,其安全问题日益突出[1],对水库大坝安全监测提出了更高要求。 变形是反映大坝在各种因素影响下综合运行性能的最直观、最重要的指标,建立大坝变形预测模型对于大坝长效运行及除险加固具有重要意义。 混凝土坝变形预测模型有统计模型、确定性模型和混合模型等[2]。 常用的统计模型有静水季节时间(HST)模型和静水温度时间(HTT)模型[3-4]。 HST 模型基于谐波函数描述温度效应,其难以揭示温度周期性变化导致的大坝变形细节特征[5]。 而HTT 模型考虑了坝体温度变化的滞后效应,但合适的温度滞后期长度还有待探讨[6]。 虽然统计模型在实际工程中得到广泛的应用,但其不可避免的缺点是统计系数没有物理意义。相反,确定性模型可以通过力学解析法或有限元、边界元、离散元等构造环境自变量与大坝变形效应量之间的确定性关系式,反映大坝的具体物理特征,但是确定性模型中温度分量和时效分量的有限元计算相当复杂[7]。 混合模型可以结合统计模型和确定性模型的优点,即先采用有限元法计算部分分量,再结合统计方法建立各分量之间的联系。
在大坝变形预测方法中多元线性回归简单易行,但其难以处理变量间的非线性关系,易影响模型的预测精度与稳定性[5]。 随着人工智能技术的发展,支持向量机(SVM)[8]、长短期记忆(LSTM)网络[9]等用于构建大坝预测模型,提升了模型预测效果。 然而,机器学习模型在应用过程中普遍存在参数难以选取、易陷入局部极值以及过拟合等问题[10]。 随机森林回归(RFR)算法[11]能有效解决多参数之间的非线性映射问题,具有预测精度高、训练速度快等优势。 RFR 训练过程中需要进行参数选取,许多学者[12]采用默认参数或网格搜索算法寻找最优参数,但该方法带有主观性,而参数选取是否合理会直接影响大坝变形预测结果。 麻雀搜索算法(SSA)[13]相较于其他智能优化算法具有较强的探索能力,在短时间内能找到全局最优点。 本文利用SSA 算法的优势,对RFR 模型进行参数优化,利用有限元模型(FEM)计算水压分量,考虑坝体温度变化及其滞后效应,最终构建基于长期气温模拟的混凝土坝变形预测混合模型(SSA-RFR-FEMHTT 模型),模拟大坝的运行性能,以期为保障大坝稳定高效运行提供技术支撑。
1 模型建立
1.1 模型因子选取
大坝变形包括由水库水位和坝体温度波动引起的可逆变形以及由坝体混凝土蠕变、碱骨料反应等非弹性效应引起的不可逆变形[2]。 大坝变形预测统计模型形式如下:
式中:δ为位移矢量,δH为水压分量,δT为温度分量,δθ为时效分量。
1)水压分量。 库水压力是大坝承受的主要环境荷载之一,水库蓄水后库水压力作用在坝体上会使坝体产生变形。 根据坝体和基岩的弹性模量,用有限元法计算上游库水深度相应的大坝变形量,并对两者进行多项式拟合,得到计算水压分量δH的公式如下:
式中:ai为拟合系数;H为库水深度;n为H最大指数,对于重力坝n取3,对于拱坝n取4。
2)温度分量。 大坝长期运行后,坝体温度的改变主要受外界气温的影响,同时考虑到坝体混凝土温度滞后效应,采用若干段前期平均实测气温作为温度因子计算温度分量δT,公式为
式中:Ti(p~q)为第i个前p天到前q天的平均实测气温,b0为回归常数,bi为回归系数。
坝体温度存在季节性和周期性变化,为反映不同时间序列长度的气温变化对大坝变形的影响,本文利用长期的气温数据,划分S1(2 个月)、S2(6 个月)、S3(1 a)和S4(2 a)4 个温度变量集计算混凝土坝变形的温度分量。 温度因子选择见表1。

表1 混凝土坝温度效应模拟变量集
3)时效分量。 时效分量描述了大坝运行过程中因坝体混凝土材料徐变、坝基岩体蠕变以及自生体积变形等因素引起的不可逆变形。 对正常运行的大坝,时效分量变化规律为初期变化急剧、后期渐趋稳定。据此规律,采用线性函数和对数函数的线性组合能较好地描述时效分量δθ:
式中:d1、d2为拟合系数,θ为测点监测的某个时间,θ0为测点监测的初始时间。
1.2 麻雀搜索算法
麻雀搜索算法[13-14]是基于麻雀种群觅食和反捕食行为的一种新型智能优化算法,麻雀觅食过程就是算法寻优过程,该算法寻优能力强、收敛速度快。 在麻雀觅食过程中,发现者主要负责寻找食物以及提供觅食的区域和方向;加入者会不断监视发现者,在发现者周围觅食;警戒者主要负责侦察预警,当麻雀种群遭遇危险时,会进行反捕食行为。
设麻雀种群由n只麻雀组成,则麻雀种群可以表示为X=[x1x2…xn]。 发现者位置更新如下:
加入者位置更新如下:
警戒者位置更新如下:
式中:Xk
best为当前全局最优位置;β为步长控制参数,服从标准正态分布;fi为适应度;fg、fw分别为当前最优、最差适应度;C为[-1,1]内随机数;ε为常数,避免分母为0。
1.3 随机森林回归模型
随机森林回归(RFR)模型主要和决策树(DT)、集成学习算法有关,决策树是基本组成单元,集成学习算法是将多棵决策树整合成森林的核心。
1)决策树。 决策树是一种简单高效的学习算法,广泛应用于分类和预测。 一棵决策树的结构包括一个根节点、若干个内部节点和若干个叶子节点。 无论是分类决策树还是回归决策树,都是从根节点开始自上而下对节点属性进行划分,生成倒置的树状结构。 决策树学习效率高,但在决策树构建过程中,每个特征处都会进行一次分裂,树的深度较大,导致最终决策树复杂度较高,且决策树存在易过拟合、预测精度低等问题。
2)集成学习算法。 集成学习算法的基本理论是将众多弱学习器结合在一起,生成一个强大的学习器。该算法可以充分利用单个弱学习器所提供的信息,集成后的学习器具有较高的精度,并且可以确保输出结果的稳定性。 集成学习算法主要有Bagging 和Boosting,这两种方法的共同点是均需重新放回抽样,不同的是Bagging 抽取训练集无须考虑权重,Boosting则需要考虑权重;另外,Bagging 中每一个训练过程应彼此独立,而对于Boosting 的训练过程是基于上一次训练结果的。
3)RFR 算法。 RFR 是集成学习算法发展过程中产生的一种组合算法,RFR 算法基于Bagging 方法将多棵分类回归树(CART)整合成森林,并将每棵CART输出结果{h(x,θt),t=1,2,…,n}的平均值h(x)作为预测值:
式中:x为自变量,θt为服从独立分布的随机变量。
4)RFR 模型超参数。 RFR 模型包含众多的超参数,有些蕴含在CART 中,有些来源于RFR 算法本身。这些超参数对于RFR 模型的预测结果具有不同程度的影响,因此需要对超参数进行调优,以提高模型拟合度和泛化能力。 为减少超参数调优的工作量,忽略部分影响较小的超参数,利用SSA 优化算法对影响较大的超参数进行调优。 待调优的超参数包括CART 的棵数和深度,这两个参数影响着RFR 模型的复杂程度和拟合能力。
RFR 模型建立与计算流程见图1,具体步骤如下:1)通过Bootstrap 随机抽样方式在原始数据样本中获取多个子样本集;2)基于每个子样本集,从特征集合中选取子特征集来构建CART;3)使每棵CART 能最大限度生长,直至满足终止条件;4)将每棵CART 预测结果按式(8)进行集成后作为RFR 模型预测值。
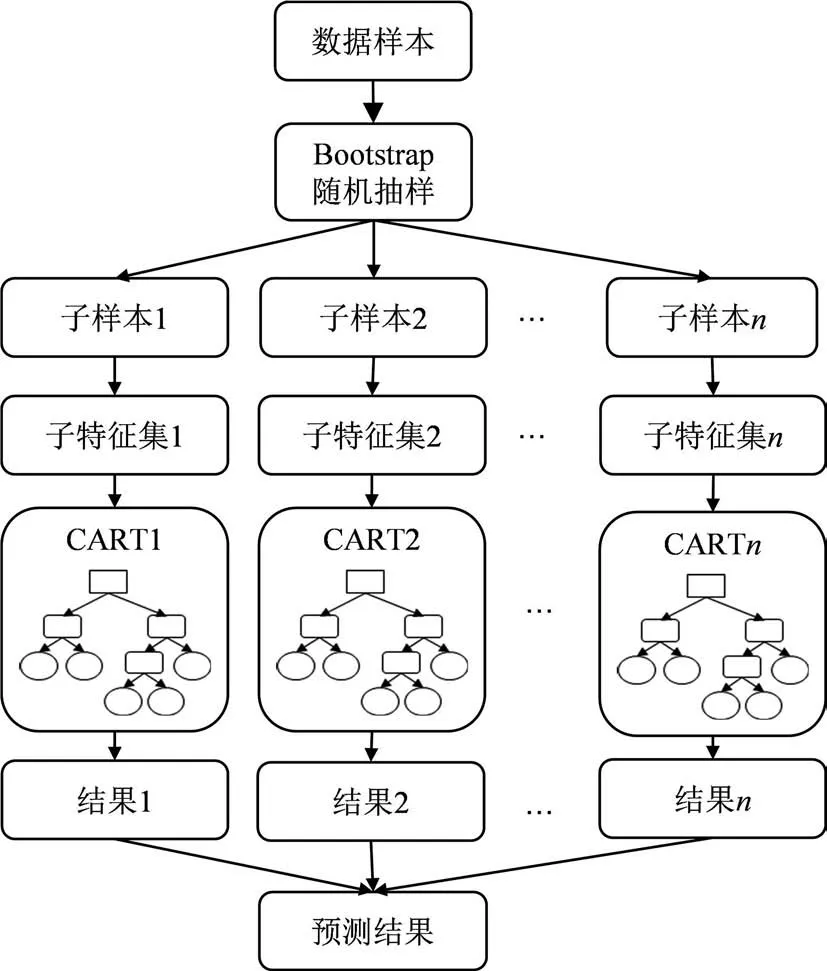
图1 RFR 模型建立与计算流程
1.4 混凝土坝变形预测混合模型构建基本流程
在考虑混凝土坝物理特征和外界气温的情况下,采用SSA 算法优化的RFR 模型建立混凝土坝变形预测混合模型,具体建模流程见图2,步骤如下:1)建立大坝有限元模型,模拟不同水位的大坝变形,得到上游水位与坝顶垂直变形关系曲线,对该曲线进行多项式拟合,得到水压分量表达式;2)确定温度和时效影响因子,将其与上一步骤中的水压分量结合作为混凝土坝变形影响因子;3)将训练集数据输入SSA-RFR 模型,通过SSA 优化算法迭代寻优,得出RFR 模型的最优参数组合;4)将预测集数据输入参数优化后的RFR模型,得到预测结果;5)选用平均绝对误差(MAE)、均方根误差(RMSE)和相关系数(R)3 个指标对混凝土坝变形预测混合模型的预测效果进行评估。
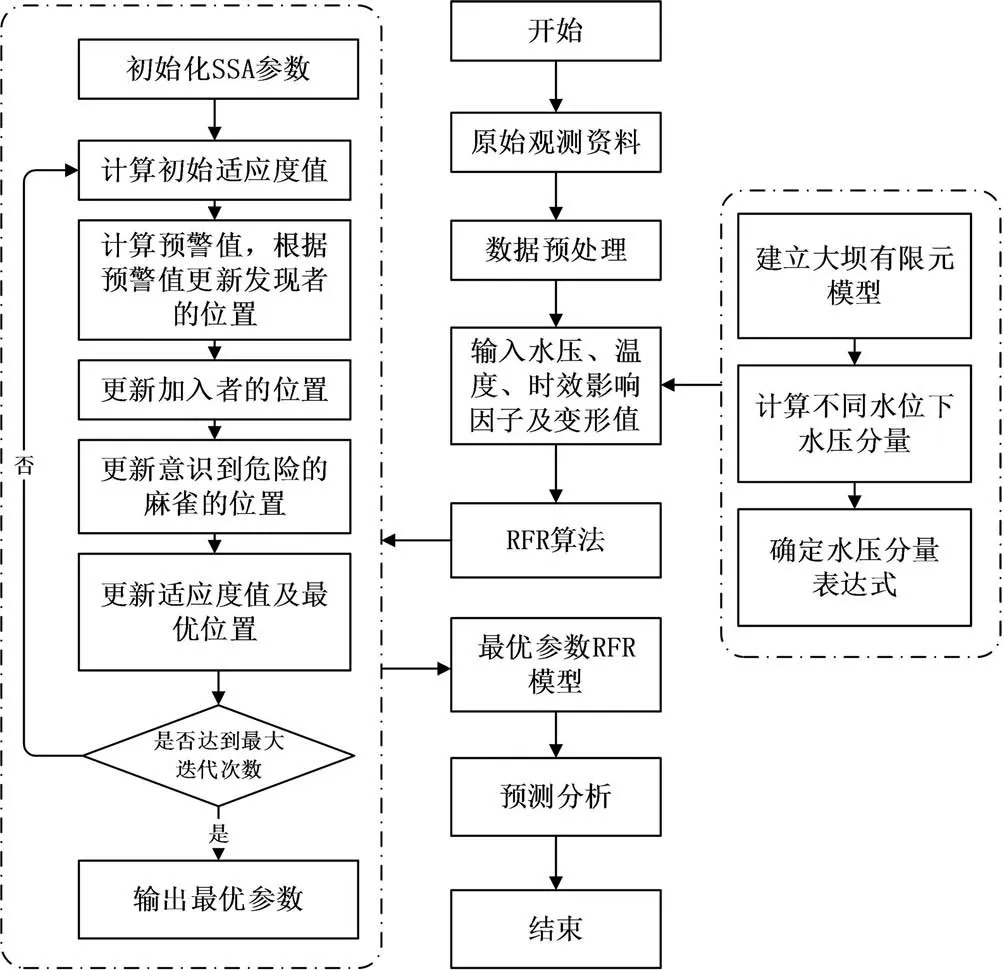
图2 混凝土坝变形预测混合模型构建流程
2 工程实例
2.1 工程概况
以安徽省某混凝土坝为例进行实践应用,挡水坝为同心圆变半径的混凝土重力拱坝。 死水位101.0 m,正常蓄水位119.0 m,校核洪水位124.6 m,总库容28.25×108m3。 坝顶高程126.3 m,最大坝高76.3 m,坝顶弧长419.0 m,坝顶宽8.0 m,最大坝底宽53.5 m。 水电站管理部门在16 个坝段的坝顶设置垂直变形测点(见图3),并利用高程控制网监测坝体垂直变形,同时每月手动测量一次坝顶变形。 以18#测点为例,使用1981 年9 月16 日—2018 年12 月12 日的450 组垂直变形数据(下沉为正、上抬为负)进行分析,将前360组(1981 年9 月16 日—2011 年6 月13 日)数据作为训练集,后90 组(2011 年7 月12 日—2018 年12 月12日)数据作为预测集。
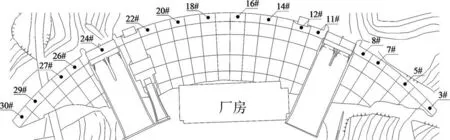
图3 某混凝土坝测点分布
采用有限元分析软件ABAQUS 建立大坝有限元模型,考虑到坝体与地基的相互作用,基岩选取范围为大坝上游方向与下游方向的基岩长度均取坝高的2 倍长度,大坝底部向下延伸的长度取坝高的1.5 倍长度,左边及右边基岩边界到大坝的长度均取坝高的1.5 倍长度。
为了使坝体整体及拱端等部位的变形更加贴近实际情况,大坝有限元模型的边界条件如下:对坝基岩体上下游基岩面方向的位移进行约束,对坝基岩体底面采用固定约束边界条件,对坝基岩体左右基岩外侧面方向的位移进行约束。 该有限元模型共划分等参单元200 856 个,节点214 351 个,有限元模型见图4。

图4 某混凝土坝有限元模型
2.2 混合模型构建结果分析
首先利用有限元方法计算初始日坝体测点在水压荷载作用下的变形并将其作为初始变形,再根据上、下游实测水位,计算坝体在不同水压荷载作用下各测点的变形值,最后得到各测点在不同水压荷载下水压分量相对于初始日的变形值。 根据有限元计算结果,通过多项式拟合得到混合模型水压分量的拟合表达式为
基于上述有限元计算结果,根据18#测点的实测数据,采用SSA-RFR 算法对目标拱坝进行建模和预测分析。 对训练集数据进行归一化处理,利用SSA 算法对RFR 模型的决策树棵数和决策树深度进行寻优。SSA 算法迭代次数设为100,种群数设为20。 温度变量集为S2 的RFR-FEM-HTT 模型和考虑不同温度变量集的SSA-RFR-FEM-HTT 模型的超参数取值见表2,SSA 算法迭代收敛过程见图5。
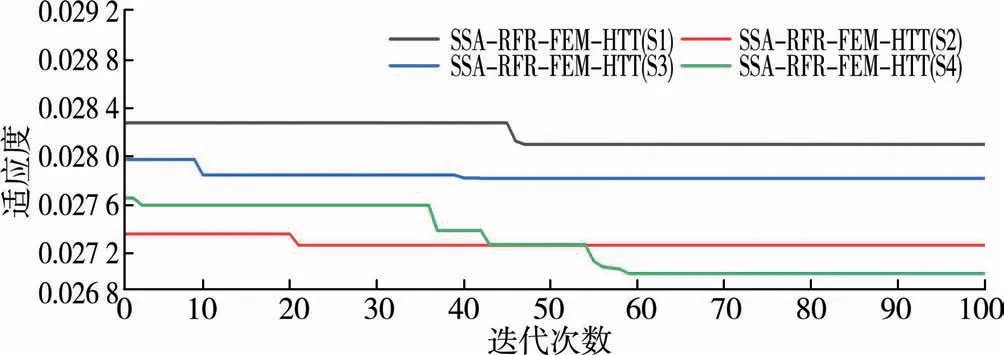
图5 SSA 算法迭代收敛过程
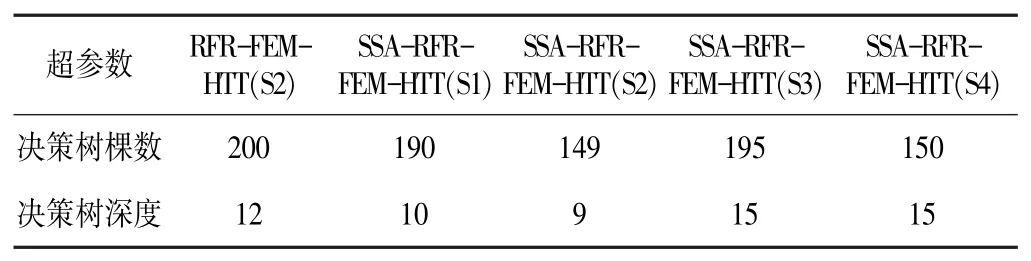
表2 各变形预测混合模型超参数寻优值
基于SSA 寻优算法得到的最优参数组合分别构建混合模型,并输入预测集数据进行预测。 为验证模型预测性能的优劣,在相同训练集数据的基础上构建基于多元线性回归(MLR)的HST、HTT 预测模型,同样对预测集数据进行预测。 各变形预测模型对应的拟合曲线见图6。 7 个模型均取得了较好的训练效果,SSA-RFR-FEM-HTT 模型相较于SSA-RFR-HTT、MLR-HST、MLR-HTT 模型拟合效果更优,考虑不同温度变量集的SSA-RFR-FEM-HTT 模型的拟合效果也有所不同。
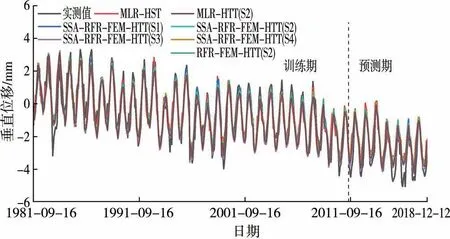
图6 各变形预测模型的拟合结果
7 个模型的预测效果比较见表3。 由表3 可知,相较于MLR-HST 模型,采用实测气温计算温度分量的大坝变形预测混合模型的平均绝对误差、均方根误差均较小、相关系数均较大。 原因是MLR-HST 模型用谐波函数描述大坝变形温度分量,忽略了坝体温度的周期性差异与局部波动导致的大坝细微变形。 相对而言,采用实测气温计算温度分量的HTT 模型考虑了坝体温度实际变化及其滞后效应,更贴近大坝实际荷载情况。
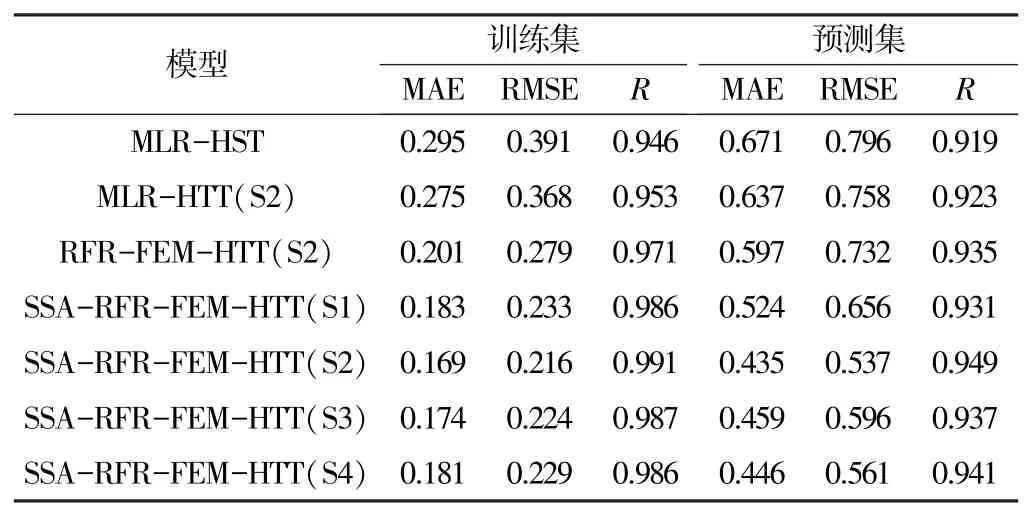
表3 各变形预测模型性能比较
对基于4 个不同温度变量集的SSA-RFR-FEMHTT 模型的模拟效果进行比较。 由表3 可知,以S2 温度变量集(6 个月)为温度因子的SSA-RFR-FEMHTT(S2)模型的预测性能最优。 大坝已经运行超过40 a,不考虑混凝土水化热影响,坝体温度和水温的变化主要受外部气温变化的影响。 同时,大坝内部坝体温度变化相对于外部气温变化存在滞后,最佳温度变量集与大坝的体积和类型有关。 在本研究中目标混凝土坝以S2 温度变量集为温度因子的模型模拟精度最高,即目标混凝土坝温度效应滞后6 个月最为合理。因此,选择S2 作为长期气温的代表变量集。 同时可知,RFR-FEM-HTT 模型和SSA-RFR-FEM-HTT 模型的预测结果都好于MLR-HST、MLR-HTT(S2)模型的,但相比于RFR-FEM-HTT 模型的,SSA-RFR-FEMHTT 模型的预测值与实际值更接近,预测效果更佳。
SSA 算法参数优化前后模型预测性能对比见表4。参数优化后,与RFR-FEM-HTT(S2)模型相比,SSARFR-FEM-HTT(S2)模型的预测性能有所提高。 其原因是采用SSA-RFR-FEM-HTT 模型预测时,SSA 算法对RFR 模型的超参数决策树棵数和深度进行全局寻优,解决了RFR 存在的参数选择敏感问题,进一步提高了模型的预测精度,由此也验证了所建立的SSARFR-FEM-HTT 模型的合理性和科学性。
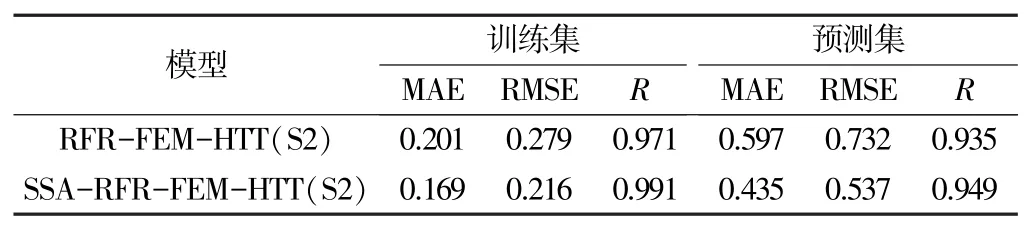
表4 参数优化前后模型预测性能比较
综上,SSA-RFR-FEM-HTT 模型的3 项评价指标明显优于MLR-HST、MLR-HTT、RFR-FEM-HTT 模型的,表明SSA-RFR-FEM-HTT 模型预测性能更高、稳定性更好。 原因主要有三点:一是考虑坝体温度变化的滞后效应,采用合适的气温数据序列长度分析坝体温度变化对大坝变形的影响;二是结合有限元方法建立混合模型,能够较好地反映大坝的具体物理特征,减少不确定因素的影响;三是利用SSA-RFR 算法解决多参数之间的非线性映射问题,有效模拟大坝变形与环境影响因素之间的函数关系,实现对大坝变形性态的准确预报。
3 结论
应用麻雀搜索算法优化随机森林回归算法解决混凝土坝变形过程中多参数之间的非线性映射问题,建立了考虑混凝土坝物理特征、温度变化和变形非线性特征的混凝土坝变形预测混合模型。 考虑到坝体温度的滞后效应,合适的气温数据变量集可以更加精准地预测混凝土坝的变形过程,通过分析得出目标混凝土坝温度变量集气温序列长度为6 个月时,模型的预测精度最高。SSA-RFR-FEM-HTT 模型相较于RFR-FEM-HTT 模型或统计模型预测精度更高,表明建立变形预测混合模型时考虑混凝土坝物理特征、温度变化以及变量非线性关系时,可以显著提高模型的预测性能。
