铝合金三明治板面外承载特性的有限元模拟和试验研究

张超锋,张大军,何 彪

(1.江南大学机械工程学院,无锡 214122;2.苏州江南航天机电工业有限公司,苏州 215300)

0 引 言

三明治板是由上下两层薄而强的面板和密度小、厚度大、承载能力相对较弱的芯板组成的,该结构可以满足刚度、强度、稳定性和轻量化要求[1-2]。然而,三明治板在受到局部载荷作用时会产生弯曲变形或者局部压入变形,可能会发生屈曲失效,进而导致结构破坏[3]。因此,深入探究三明治板的结构稳定性具有重要意义。由铝合金和聚氨酯泡沫组成的铝合金三明治板具有密度小、强度高和隔热保温等特点,广泛应用于方舱结构中[4]。铝合金三明治板的面外稳定性是影响方舱结构可靠性的重要因素。传统面外屈曲研究通常集中在单块薄板上[5],载荷类型[6]、边界条件[7]、形状系数[8]、尺寸效应[9]和材料属性[10]是影响薄板屈曲失稳的重要因素,薄板的抗面外失稳能力很弱。可通过借鉴经典薄板理论对三明治板进行等效分析,常用的等效分析方法包括试验法、解析法和有限元模拟[11]。目前,有关三明治板等效屈曲的研究主要集中在玻璃纤维-聚氨酯泡沫[12]和钢-聚氨酯泡沫[13]等方面,尚未见有关铝合金三明治板等效屈曲的研究报道。

基于此,作者通过有限元模拟方法研究了点载荷和面载荷作用下不同长宽比和宽厚比铝合金三明治板的面外屈曲特性,并通过试验对模拟结果进行验证;通过试验研究了不同尺寸参数铝合金三明治板的破坏模式、面外承载能力以及屈曲比,以期为合理评估铝合金三明治板的力学性能和结构稳定性提供依据,进而为方舱结构的轻量化设计奠定基础。

1 试样制备与试验方法

1.1 试样制备

试验材料包括厚度为1.2 mm 的5052铝合金面板以及厚度为49 mm 的聚氨酯泡沫芯板,均由江南航天机电工业有限公司提供。采用粘接成型法制备三明治板。在固定的模具内发制泡沫芯板,在120～130℃下固化成型,并将表层硬皮及硬皮下的扁平气泡全部切除,然后将芯板按试验尺寸进行切分。将打磨好的面板和芯材用WD3705胶黏剂黏结,并采用pu3-10m型压制机在70℃,5 MPa下加压并保温2 h,室温放置24 h后,得到总厚度为51.4 mm的三明治板。

在实际应用中常规方舱大板宽度为2 400 mm,为提高结构承载能力,通常在宽度方向设计1～2根梁,因此将三明治板的宽度定为700 mm 和1 100 mm,在此基础上设置5种长度,探讨不同长宽比对三明治板承载能力的影响,具体的尺寸参数如表1所示。通过试验验证,三明治板的黏结性能均符合GJB 2093A—2012中的实际工程应用标准要求。

1.2 试验方法

按照GB/T 1453-2005,采用1000 KN瑞格尔(REGER)型低周疲劳液压试验机对试样进行点/面载荷准静态压缩试验,试验机主要由控制系统、试验简支平台和数据采集系统组成,其中试验简支平台由截面尺寸为40 mm×40 mm 的铝型材搭建而成。通过G字夹将试样固定在试验简支平台上。按照GJB 2093A-2012,选用点载荷和面载荷进行试验,点载荷加载面积为10 mm×10 mm,载荷为1 k N,面载荷加载面积为500 mm×500 mm,载荷为3 k N。试验采用控制位移的加载方式,设定压缩速度为0.03 mm·s-1。点载荷施加到试样破坏为止,面载荷位移施加到25 mm 停止。通过数据采集系统得到载荷-位移曲线。

2 有限元模型

采用ANSYS Workbench软件分析三明治板在不同载荷类型下的力学性能。铝合金面板采用壳单元,聚氨酯泡沫芯板采用实体单元。支撑板、加载板和压头均设置成刚体约束。通过网格无关性分析可知,当三明治板整体网格数量达到4×106时,能够获得较高的计算精度。三明治板的网格总数量是4 235 440。有限元模型如图1所示,三明治板全部采用六面体网格,同时点载荷压头区域的网格需进行加密。铝合金面板和聚氨酯泡沫芯板采用绑定接触类型。在仿真中压头只提供z方向自由度,并将下面板与平台上方四周完全固定。铝合金和聚氨酯泡沫的性能参数[10]如表2所示。

图1 点载荷和面载荷下的有限元模型网格划分Fig.1 Finite element model meshing under point loading(a)and surface loading(b)

表2 铝合金和聚氨酯泡沫的性能参数Table 2 Material properties of aluminum alloy and polyurethane foam

3 模拟结果与分析

3.1 面外屈曲变形

由图2可以看出:在点载荷作用下,试样上面板出现明显的面外位移量,形成了试样中心突出的屈曲变形;随着长宽比的增大,试样变形区域增大,但是集中变形区域的直径从53 mm 缩小到38 mm。

图2 点载荷下13.6宽厚比及不同长宽比试样的屈曲变形模拟结果Fig.2 Simulation of buckling deformation of specimens with width-to-thickness ratio of 13.6 and different length-to-width ratios under point load

由图3可以看出,在面载荷作用下,试样上面板出现明显的面外屈曲变形,试样中心处变形量较大。当长宽比为1.0时,试样变形区域的长度是面载荷加载边长的1.3倍;当长宽比增大到1.6时,变形区域的长度扩大至面载荷加载边长的1.9倍。这说明在相同宽厚比下,试样变形区域的长度随着长宽比的增大而增大。这是因为长宽比的增大导致试样的弯曲刚度降低,抵抗变形的能力降低,因此试样变形区域逐渐增大[14]。

图3 面载荷下13.6宽厚比及不同长宽比试样的屈曲变形模拟结果Fig.3 Simulation of buckling deformation of specimens with width-to-thickness ratio of 13.6 and different length-to-width ratios under surface load

3.2 应力分布

由图4可以看出,在点载荷作用下,试样中心处的应力较集中。当宽厚比一定时,试样应力集中区域的直径随长宽比的增大而增大。当长宽比为1.6时,应力集中区域直径是长宽比为1.0试样的2倍。当长宽比较小(1.0)时,试样的刚度较大,面板整体抗面外变形能力强,载荷则主要集中在压头区域,因此随着压头的不断加载,压头周边区域容易发生较大的塑性变形;当应力达到铝合金板的破坏强度时,压头刺穿铝合金,周边伴随着较大的塑性变形区域。当长宽比较大(1.6)时,试样刚度变小,面板整体抗面外变形能力变弱,因此在压头不断加载作用下,面板整体发生变形的面积较大,而压头周边发生塑性变形的区域较小;随着面板变形量的增大,压头周边的集中载荷效应明显,当达到面板的破坏强度时,试样会沿压头边缘发生瞬时断裂。

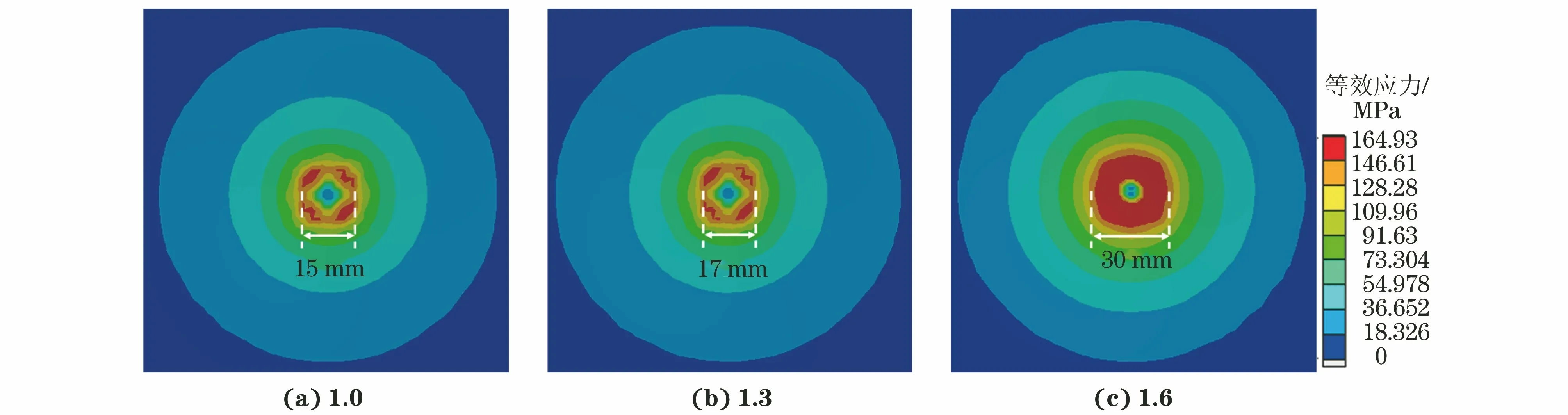
图4 点载荷下13.6宽厚比及不同长宽比试样的应力分布模拟结果Fig.4 Stress distribution simulation of specimens with width-to-thickness ratio of 13.6 and different length-to-width ratios under point load

由图5可以看出,在面载荷作用下,试样面板上位于压头四周的应力大于试样边缘的应力。随着长宽比的增大,试样应力分布长度从676 mm 逐渐减小到550 mm,这表明同一宽厚比下,试样应力分布长度与长宽比呈负相关。随着长宽比的增大,试样弯曲刚度降低,导致试样发生整体变形的区域长度增大,因此应力分布长度减小[15]。

图5 面载荷下13.6宽厚比及不同长宽比试样的应力分布模拟结果Fig.5 Stress distribution simulation of specimens with width-to-thickness ratio of 13.6 and different length-to-width ratios under surface load

4 试验验证与结果分析

4.1 破坏模式

由图6可以看出,在点载荷作用下,试样上面板有明显的穿孔和凹坑,试样的最终破坏模式为整体刺穿。在点载荷作用下,试样发生局部压入变形,压头附近的变形区域逐渐扩大。随着压头位移的持续增加,当所施加应力达到上面板的破坏强度时,面板发生断裂。在面板被刺穿之后,由于芯板的强度较低,试样快速发生整体刺穿。试样在压头周边处存在明显的塑性变形区域,发生破坏时的变形区域与模拟得到的试样面外屈曲变形区域大致吻合,且区域直径均随着长宽比的增大而减小。

图6 点载荷下13.6宽厚比及不同长宽比试样的破坏形貌Fig.6 Failure morphology of specimens with width-to-thickness ratio of 13.6 and different length-to-width ratios under point load

在面载荷作用下,当加载位移为25 mm 时,试样未观察到明显破坏,最终破坏模式均为芯板压缩破坏,典型的破坏形貌如图7所示。由于面载荷加载面积较大,加载结束后,从正面看整个加载区域与加载区域边缘没有出现明显的凹陷,但是从侧面看,聚氨酯泡沫芯板中间出现部分压缩现象,厚度方向的残余变形量为0.6 mm。由于残余变形量比较小,因此压缩破坏现象并不显著。

图7 面载荷下试样的典型破坏形貌Fig.7 Typical failure morphology of samples under surface load:(a)front view and(b)side view

4.2 载荷-位移曲线

4.2.1 点载荷作用

由图8可以看出:有限元模拟得到的点载荷下试样的载荷-位移曲线与试验结果基本吻合,二者的平均相对误差仅为2.3%,验证了有限元模拟的可靠性;在点载荷作用下,所有试样的极限载荷均大于GJB 2093A-2012标准规定的加载面积为10 mm×10 mm时载荷不低于1 kN的要求,载荷和位移之间均呈线性关系,载荷达到峰值后瞬时下降。当宽厚比为13.6,长宽比不大于1.3时,试样的载荷-位移曲线的斜率几乎相等,而当长宽比大于1.3时,曲线斜率明显减小,这是因为当长宽比大于1.3时,试样受到挠曲变形的影响,导致一次刚度减小,弯曲刚度逐渐减弱。当宽厚比为21.4时,不同试样的载荷-位移曲线几乎重叠,斜率与宽厚比为13.6且长宽比大于1.3试样的斜率相似,这表明当宽厚比为21.4时,所有试样的挠曲变形程度均较大。

图8 点载荷下不同尺寸参数试样的载荷-位移曲线Fig.8 Load-displacement curves of specimens with different dimensional parameters under point load:(a)width-to-thickness ratio of 13.6 and(b)width-to-thickness ratio of 21.4

4.2.2 面载荷作用

由图9可以看出:有限元模拟得到面载荷作用下试样的载荷-位移曲线与试验结果基本吻合,平均相对误差为3.1%,验证了有限元模拟的可靠性;在面载荷作用下,所有试样的极限载荷均大于GJB 2093A-2012标准规定的加载面积为500 mm×500 mm 时载荷不低于3 k N 的要求。所有试样的载荷-位移曲线均呈先线性增加后趋于平稳的趋势,分为弹性阶段和塑性阶段。在弹性阶段,载荷-位移曲线几乎重叠。在塑性阶段,随着长宽比的增大,曲线斜率变小,试样的二次刚度下降。说明随着长宽比的增大,试样的弯曲刚度下降,导致承载能力降低。同时,试样在塑性阶段的载荷随着位移的增加而缓慢增大,这是由泡沫受载后逐渐被压缩导致的。当材料处于塑性阶段时,试验载荷略小于模拟载荷,这是由于聚氨酯泡沫属于孔介质材料,抗压性能差,而仿真建模是均质实体建模。

图9 面载荷下不同尺寸参数试样的载荷-位移曲线Fig.9 Load-displacement curves of specimens with different dimensional parameters under surface load:(a)width-to-thickness ratio of 13.6 and(b)width-to-thickness ratio of 21.4

4.3 面外承载能力

由图10可以看出:当宽厚比为13.6时,随着长宽比的增大,点载荷作用下试样的破坏载荷呈现先升高后趋于平稳的趋势。这是因为当长宽比不大于1.3时,试样主要以刚性变形为主,因此破坏载荷随长宽比的增大而增大。而当长宽比大于1.3时,试样的破坏载荷不受长宽比的影响。当宽厚比为21.4时,随着长宽比的增大,点载荷作用下试样的破坏载荷基本不变,保持在2 500 N,这是由于此时达到了材料的极限承载能力。随着长宽比的增大,面载荷作用下不同宽厚比试样的屈服载荷均呈降低趋势。这是因为随着长宽比的增大,试样的弯曲刚度降低,导致其抵抗变形能力降低,因此承载能力下降[15]。当长宽比相同时,点载荷作用下宽厚比21.4试样的破坏载荷大于宽厚比13.6试样,而面载荷作用下,宽厚比13.6试样的屈服载荷大于宽厚比21.4试样。这是因为当宽厚比为13.6时,试样刚度较大,点载荷下试样整体变形量较小,集中载荷效应明显,这加速了试样的破坏,因此其承载能力小;而在面载荷作用下试样表现为整体受力,抗弯承载能力更强。面载荷作用下试样的屈服载荷均高于点载荷作用下的破坏载荷。这是由于点载荷作用面积小于面载荷作用面积。因此,载荷类型对试样的承载能力影响显著。

图10 试验得到不同尺寸参数试样在点载荷下的破坏载荷和面载荷下的屈服载荷Fig.10 Failure load under point load(a)and yield load under surface load(b)of specimens with different dimensional parameters obtained from test

4.4 屈曲比

由图11可以看出:点/面载荷作用下,当宽厚比不变时,试样的面外位移量随着长宽比的增大呈现先增大后趋于平稳的趋势。同一长宽比下,宽厚比21.4试样的面外位移量大于宽厚比13.6试样。这是因为随着宽厚比的增大,试样弯曲刚度降低,导致其抵抗变形能力减弱,面外位移量增大。

图11 点载荷和面载荷下不同尺寸参数试样的面外位移量Fig.11 Out-of-plane displacement of specimens with different dimensional parameters under point load(a)and surface load(b)

为了满足试样的刚度要求,三明治板的最大允许相对挠度为1/220,最大转角为0.004 5°[4]。由于三明治板的最大宽度为1 100 mm,其所允许的最大变形量为3 mm。因此在标准点/面载荷作用下,选取面外位移为3 mm 的点作为试样面外屈曲变形的临界点,从而计算出试样面外屈曲变形临界点的屈曲比。

依据三明治板和等效单层板的弯曲刚度和扭转刚度相等,可以求出三明治板的等效弹性模量Ee和泊松比

式中:Ef,μf分别为面板的弹性模量和泊松比;h,k分别为芯板和面板的厚度;he为等效单层板的厚度。

等效三明治板的屈曲比R的计算公式[5]为

式中:τy为三明治板的剪切应力;σy为三明治板的屈服应力;b/t,b/a分别为三明治板的宽厚比和宽长比;K为屈曲系数。

根据式(1)～式(5)绘制得到的点载荷和面载荷下不同宽厚比试样的屈曲比随宽长比的变化曲线如图12所示。由图12可知,当面外位移量为3 mm时,由三明治板所对应的长宽比和宽厚比计算所得的临界屈曲比均为0.093。标准面载荷的加载面积是点载荷的2 500倍,面载荷是点载荷的3倍,而标准点载荷和面载荷在面外屈曲变形临界点的屈曲比是相等的。当屈曲比不大于临界值时,试样不会产生面外屈曲;而当屈曲比大于临界值时,试样会产生面外屈曲而导致面外失稳。

图12 不同宽厚比试样的屈曲比随宽长比的变化曲线Fig.12 Curves of buckling ratio vs width-to-length ratio of specimens with different width-to-thickness ratios

5 结 论

(1)通过ANSYS软件模拟得到的点载荷和面载荷下试样的载荷-位移曲线与试验结果基本吻合,二者的平均相对误差小于5%,证明了有限元模拟的可靠性;在点载荷和面载荷作用下,不同尺寸参数三明治板的极限载荷均满足GJB 2093A—2012标准要求;点载荷作用下三明治板的破坏模式为整体刺穿,而面载荷作用下三明治板发生芯板压缩破坏。

(2) 在点载荷作用下,当宽厚比为13.6时,随着长宽比的增大,三明治板的破坏载荷先升高后趋于平稳,而当宽厚比为21.4时,破坏载荷基本不变,保持在2 500 N;当长宽比相同时,宽厚比21.4三明治板的破坏载荷大于宽厚比13.6三明治板。在面载荷作用下,随着长宽比的增大,不同宽厚比三明治板的屈服载荷均呈降低趋势,宽厚比13.6三明治板的屈服载荷大于宽厚比21.4三明治板。

(3) 以3 mm 为面外屈曲变形临界值时,点/面载荷作用下三明治板的临界屈曲比均为0.093。