松砂中倾斜锚板上拔承载特性模型试验研究

李姝雨, 邹润超,2, 俞 快, 原 媛, 史旦达

(1.上海海事大学 海洋科学与工程学院, 上海 201306; 2.上海浦东水务(集团)有限公司, 上海 201399)

1 研究背景

锚板基础是一种抗拔基础,在建筑工程、海洋工程等领域已得到广泛应用。锚板基础上拔时,其承载力需由锚周土体的变形来提供,但由于锚-土相互作用的复杂性,目前已有的研究和分析还不够完善,并且现有国内外研究大多集中于锚板的垂直上拔,而针对倾斜锚板上拔承载机制的研究相对较少。因此,研究土体中倾斜锚板的上拔承载特性具有现实意义。

针对锚板上拔承载特性的研究,现阶段主要采用数值模拟[1-3]和试验研究[4-7]等方法。已有研究表明,锚板的上拔承载力和土体破裂面模式主要受到锚的几何形状、锚体埋置深度、土体密度等因素影响。Nazir等[8]研究了干砂中锚板垂直上拔特性,结果表明,上拔承载力随埋深比和砂土密度的增大而增大,而受轴径比的影响较小,在松散砂中可观察到局部破坏面,在密实砂中可观察到截锥状破坏面。袁驰等[9]通过三维有限元模型数值分析发现,松砂中浅埋破坏发生在埋深比H/D≤4时(H为锚板埋深,D为锚板直径),此时滑裂面外扩角随埋深的增加而增加;深埋破坏发生在埋深比H/D≥6时,此时滑裂面为气泡状。Salehzadeh等[10]采用离心机模型试验并结合数字图像技术分析了锚板上拔承载机理,结果表明,埋深对锚板的破坏机制影响较大,将H/D=4～5确定为临界埋深比,此埋深比区分了锚板的浅埋和深埋状态。除此之外,也有研究表明[11-13],锚板的上拔承载力和破裂面模式与锚板埋置时的倾斜角度密切相关,在实际工程中,斜锚能够比水平锚或垂直锚更好地抵抗上拔力和倾覆力矩。Mukherjee等[11]通过室内模型试验研究了干砂中倾斜锚板的抗拔能力,结果表明,在无筋土和加筋土中,锚板的抗拔能力均随着倾斜角度的增大而增大。石恒俊等[12]通过砂土中锚板抗拔模型试验发现,随着倾斜角度的增大,锚板的抗拔性能有所降低,但这一趋势随着埋深的增大有所减弱。胡伟等[14]研究表明,上拔承载因子Nγ随埋深比的增加呈先快后慢的增大趋势,直至趋于一渐进值,锚周土体滑动面随埋深比和倾斜角度的演化可用椭圆来刻画,此椭圆的长短轴比随埋深比的增大而减小,椭圆大小不受倾斜角度的影响。

数字图像相关技术(digital image correlation, DIC)因其具有非接触、精度高、动态高效等诸多优点,目前已被广泛应用于岩土体变形测量研究方面[15]。例如,张昕等[16]采用DIC技术观察了群锚上拔过程中土体的位移场和应变场,结果表明,群锚上拔承载力的叠加效应比较明显,且砂土密实度、锚体埋深和锚体间距会对这种叠加效应产生较大影响。史旦达等[17]对圆形锚板上拔时锚周砂土的变形特性进行了试验研究,重点对埋深比、砂土相对密度和盘径产生的影响进行了分析,试验结果表明,浅埋时土体剪切破坏面沿锚板边缘垂直向土体表面开展;深埋时土体剪切破坏面沿锚板边缘向内侧斜上方发展,且锚板盘径变化不影响上拔时锚周土体的变形特性。

本研究以福建标准砂作为填料,在松砂中开展了倾斜锚板上拔的室内模型试验。试验通过数字图像相关技术着重分析了锚板上拔时锚周土体的变形特性(即位移场、剪应变场和体应变场),探讨了倾斜角度(倾角)和埋深比对上拔承载性能及土体变形特性的影响,试验结果有助于揭示倾斜锚板上拔承载规律及其机理。

2 试验方法

2.1 数字图像相关技术

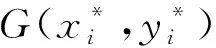
(1)

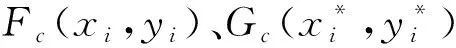
对测量得到的位移场进行差分处理后,可得土体剪应变场和体应变场,计算公式为:

(2)

式中:γxy为剪应变;εv为体应变,数值为正时表示体积膨胀,数值为负时表示体积收缩;εx、εy分别为x和y方向上的正应变,本文中规定拉为正、压为负。

本试验中,计算机控制摄像机以9 Hz的频率进行连续拍摄,所采集的数字图像分辨率为3 376×2 704像素。

2.2 试验设备

模型试验装置如图1(a)所示,试验中使用的钢质模型箱尺寸为长800 mm、宽600 mm、高800 mm,模型箱的前壁为有机玻璃,有机玻璃的厚度为10 mm。试验设备包括控制锚杆上拔速度的减速电机、力和位移传感器(力传感器量程为2 000 N、精度为0.01 N;位移传感器量程为1 300 mm、精度为1 m)、JHYC-40静态应变测量系统等,计算机中安装有JHYC静态应力测量分析系统和Spinview图像采集系统,数字图像由配置了高清CCD镜头的高分辨率相机拍摄得到。锚板的倾角通过加载装置顶部可调节升降的刚性支架进行调整,如图1(b)所示。试验过程中,控制减速电机以0.3 mm/s的速度将锚板沿杆身方向拔出,上拔过程中,记录上拔力和上拔位移,上拔力和上拔位移均沿杆身方向。

图1 倾斜锚板上拔模型试验系统 图2 锚体模型(单位:mm)

由于DIC变形分析的需要,模型锚体采用半模,由不锈钢制成。锚杆杆身长度为850 mm、直径为5 mm,锚板直径D为50 mm、厚度为5 mm,锚体模型如图2所示。

在试验准备阶段,为提高试验精度,需要通过改变由升降装置组成的加载装置顶部的刚性支架的位置来控制锚杆倾角,顶部刚性支架的两端中的一端的底部置有金属垫片,另一端则紧贴模型箱的顶部横梁,支架由4颗L型螺丝钢与模型箱顶部横梁完成固定,固定完成后使用数显角度尺进行测量,以确保锚杆倾角的准确。除此之外,还需要在锚杆上拔过程中使半模锚片紧贴有机玻璃的表面,然后调节相机的水平位置、支座高度和进光量等,保证拍摄过程中相机光学轴垂直于有机玻璃表面,从而确保采集图像的清晰度以及后期图像处理中位移场等信息的精确性。

2.3 试验砂料

试验以福建标准砂作为砂样,此砂样的粒径大小在0.075～2 mm范围内,平均粒径为0.34 mm,颗粒比重为2.643,最大和最小孔隙比分别为0.848和0.519,不均匀系数为1.542,曲率系数为1.104。

采用砂雨法[20]制备松砂试样,落砂高度控制为10 cm,砂样的相对密度为32%～44%,干重度γ为13.23～13.82 kN/m3,平均干重度为13.52 kN/m3,由直剪试验测定松砂的内摩擦角为30.9°。

在试样制备阶段,锚板被预埋于砂样中再进行上拔试验,预埋时保证锚板底部与模型箱底部之间的距离不小于80 mm。根据Sakai等[21]的研究,当锚板底部与模型箱底面的距离超过80 mm后,模型箱底部边界不会对锚板上拔时土体的变形规律产生显著影响。

2.4 试验工况

以锚板的倾角θ和埋深比H/D为主要参数来设计试验工况,杆身倾斜角度(杆身与竖直方向的夹角)分别取0°、5°、10°、15°和20°,锚板埋深比H/D分别取1、2、…、9。

3 锚板上拔承载特性分析

3.1 埋深比的影响

图3给出了松砂中锚板不同倾角时埋深比对上拔力F-上拔位移δ曲线的影响。分析图3可知,在松砂中,埋深比的变化基本不影响上拔曲线的发展形态,不同埋深比的上拔曲线均为先上升后下降的变化趋势;但埋深比影响上拔力峰值大小及其位移水平,保持倾角θ不变时,随着埋深比的增加,上拔力峰值Ff增大,所对应的水平位移δf也随之增大。以θ=5°为例(图3(b)),当H/D=1时,Ff为2.5 N,δf为2.7 mm;H/D=3时,Ff增至21.3 N,δf增至8.32 mm;H/D=5时,Ff增至52.5 N,δf增至8.68 mm;H/D=8时,Ff达到86.1 N,δf达到8.20 mm。此外,倾斜角的变化基本不影响上述规律,但θ越大,上拔曲线达到峰值后下降得越快。

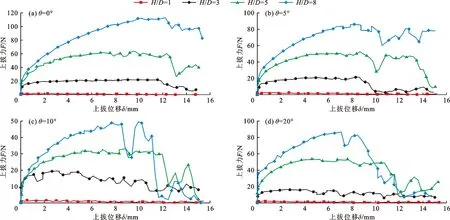
图3 锚板不同倾角时埋深比对上拔力-上拔位移曲线的影响

3.2 倾斜角度的影响

图4给出了松砂中锚板不同埋深比时倾角对上拔力F-上拔位移δ曲线的影响。由图4可知,当埋深比相同时,不同倾角锚板的上拔曲线发展形态基本一致,但锚板埋深比的变化会对这一规律产生一定的影响。在H/D=1的条件下,θ为0°、5°、10°、20°时,上拔力与上拔位移的关系曲线较为接近,且Ff处于1.5～2.7 N之间,δf均在0.5 mm左右;仅θ=15°时的上拔曲线高于其他倾角的上拔曲线,Ff和δf值也比其他倾角的相应值更大。在H/D=3的条件下,当θ从0°增至15°时,Ff和δf均逐渐减小;当θ继续增至20°时,Ff和δf均明显大于θ=15°时的相应值。当H/D为5和8时,θ从0°增至10°,Ff均逐渐减小,δf也随之减小;当θ继续从10°增至20°时,Ff和δf明显逐渐增大。上述变化规律将在下文中做进一步讨论。

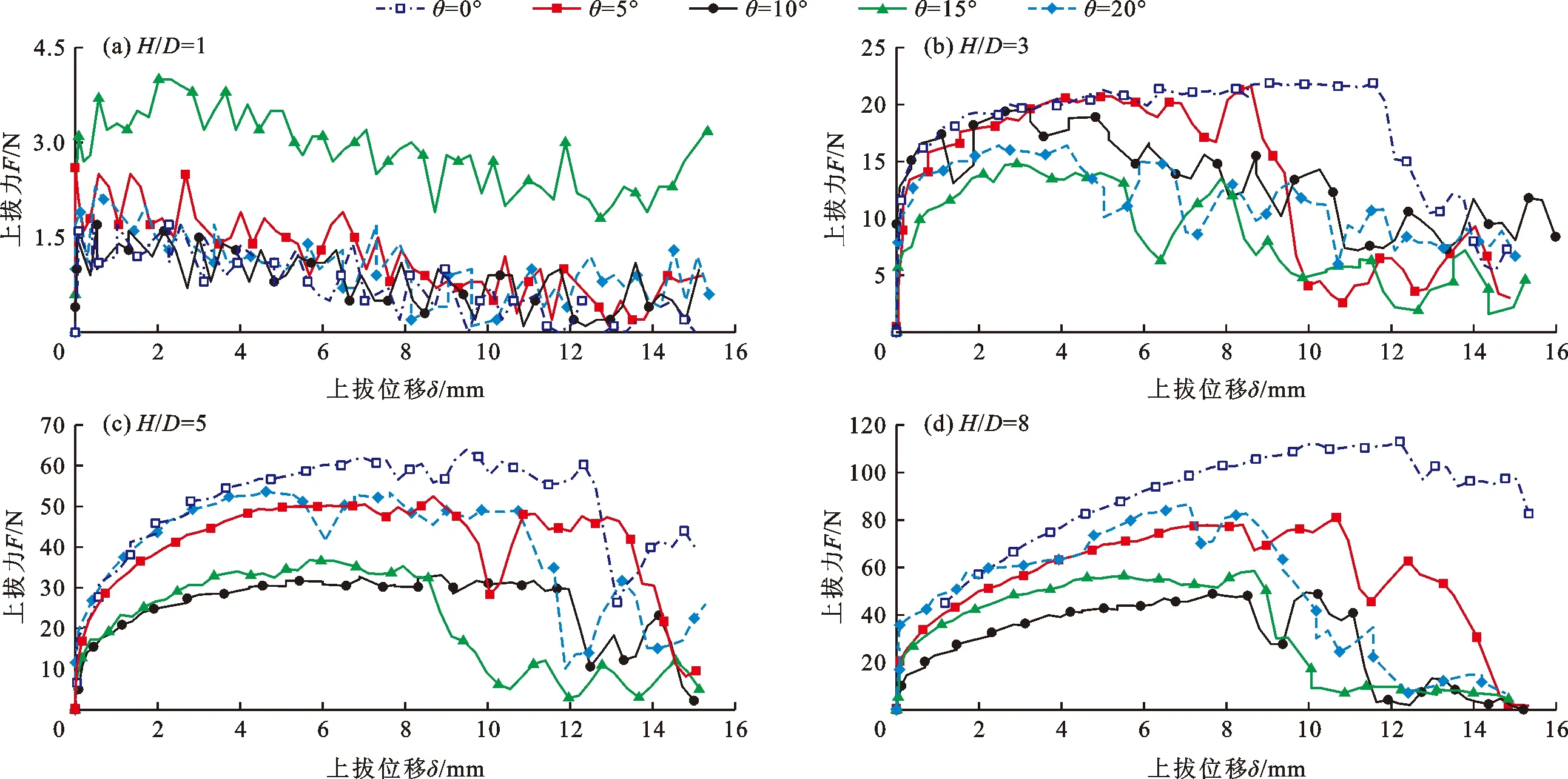
图4 锚板不同埋深比时倾角对上拔力-上拔位移曲线的影响

3.3 上拔承载力系数分析

根据Tong等[22]的研究,锚板的上拔承载力系数Nγ可以体现锚的抗拔能力,锚的上拔承载力系数Nγ可以通过公式(3)计算得出。

(3)

式中:Ff为上拔力峰值,kN;γ为土的有效重度(计算时取平均有效重度),kN/m3;A为锚板面积,m2;H为锚板埋深,m。

汇总不同倾角和埋深比情况下得到的上拔承载力系数Nγ值,绘制上拔承载力系数与埋深比及倾角的关系,如图5所示。由图5可知,锚板不同倾角下,Nγ均随着埋深比H/D的增加而增大,倾角对Nγ-H/D曲线的影响具有明显的区间性,当倾角在10°～15°范围时,Nγ数值较小(图5(a)),这一规律对于埋深较大的情况(本例中H/D=5,8),表现得尤为明显(图5(b))。关于上述现象的原因及内在机理将在下文中做进一步讨论。

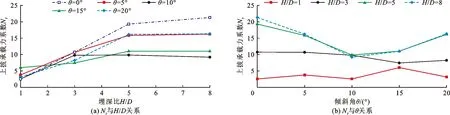
图5 上拔承载力系数与锚板埋深比及倾角的关系

需要特别说明的是,根据本文作者之前的模型试验研究[17],当采用半模试验分析上拔承载力特性时,上拔承载力系数会受到模型箱侧向玻璃边界的影响,但这种影响并不显著,与全模试验相比,上拔承载力系数的差异在9%范围之内。由此可认为,采用半模和全模分析得出的锚板上拔承载特性在宏观上差异不大,因此,本文中的半模试验方法可以用于锚板上拔时周围土体的变形分析。

4 锚板上拔松砂变形特性分析

4.1 埋深比的影响

以θ=15°为例,埋深比H/D分别取值为1、2、…、9,研究锚板埋深比对锚周松砂的位移场、剪应变场和体应变场的影响。

4.1.1 埋深比对位移场的影响 图6为不同埋深比下上拔承载力峰值时锚周松砂的位移场矢量图(图中选取H/D=1,2,3,5,8,9的试验结果进行讨论,下同)。

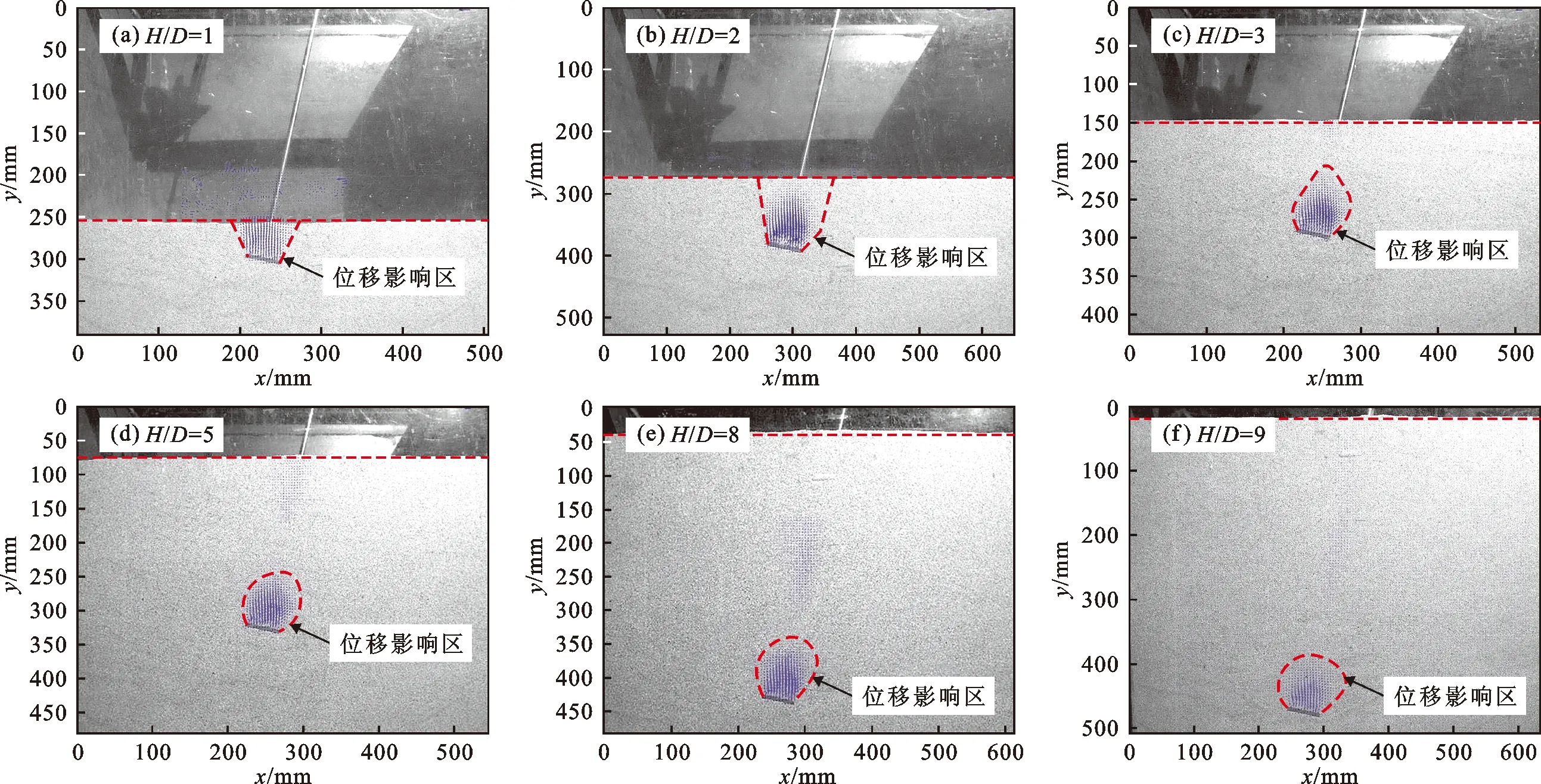
图6 不同埋深比上拔承载力峰值时锚周松砂的位移场(θ=15°)

由图6可知,随着埋深的增加,锚周松砂位移场影响区域的形状也随之改变。当H/D为1、2时,即为浅埋状态,松砂位移影响区呈扩展至砂样表面的倒锥形,表现为整体破坏;当H/D增至3时,位移影响区的形状变为内置于土体的贝壳形,此时破坏模式已由整体破坏转变为局部破坏。当H/D为5、8、9时,对于松砂而言,锚体已处于深埋状态,松砂位移影响区的形状较为相似,但位移矢量随着埋深比的增加而增大,且向锚杆倾斜侧集中。

4.1.2 埋深比对剪应变场的影响 图7为θ=15°时不同埋深比下上拔承载力峰值时锚周松砂的剪应变场(图中β1和β2为剪切破坏面与锚板的夹角)。由图7可知,在任意埋深比条件下,剪应变值从锚板边缘的最大值沿着锚板两侧逐渐减小,破坏模式为典型的渐进破坏。当H/D=1、2时,破坏模式为整体剪切破坏,剪应变场为截头倒圆锥形;当H/D=3时,破坏模式从整体剪切破坏向局部剪切破坏发展,锚周松砂的剪应变场变为正立的截头圆锥形,剪切破坏面变为向锚板边缘内侧发展;当H/D=5时,破坏模式为局部剪切破坏,锚杆倾斜侧剪切破坏面相比于H/D=3时基本不变,另一侧的剪切破坏面继续向内侧偏转了8.1°;当H/D=8、9时,剪切破坏面与锚板的夹角分别增大至84.6°和87.8°、84.5°和81.5°,因此,深埋时剪切破坏面与锚板之间接近垂直状态。

图7 不同埋深比上拔承载力峰值时锚周松砂的剪应变场(θ=15°)

4.1.3 埋深比对体应变场的影响 图8为θ=15°时不同埋深比下上拔承载力峰值时锚周松砂的体应变场。由图8可知,锚板处于不同埋深比时,其周围邻近砂体的应变场均为正值,即砂体发生体积膨胀,而砂体的体积收缩主要发生在锚板上方的一定范围内。当H/D=1时,锚板处于浅埋状态,此时在锚板上、下各(1/4)D的范围内为砂体体积膨胀区,最大体积膨胀量为4%;膨胀区上方为体积收缩区,最大体积收缩量为6%;当H/D=3时,在锚板上、下各(1/2)D的范围内为砂体体积膨胀区,最大体积膨胀量为4%,膨胀区上方为砂体体积收缩区,最大体积收缩量为3%。随着H/D的逐渐增加,膨胀区和收缩区的分布与H/D=3时较为类似,但最大体积膨胀量的数值会增大,最大体积收缩量则变化不大,例如,当H/D达到9时,最大体积膨胀量增至15%,最大体积收缩量仅为5%。

图8 不同埋深比上拔承载力峰值时锚周松砂的体应变场(θ=15°)

4.2 倾斜角度的影响

以H/D=5为例,锚板倾角θ分别取值为0°、5°、10°、15°和20°,研究锚板倾角对锚周松砂的位移场、剪应变场和体应变场的影响。

4.2.1 倾斜角度对位移场的影响 图9为不同倾角下上拔承载力峰值时锚周松砂的位移场矢量图(图中选取θ=0°、5°、10°、20°的试验结果进行讨论,下同)。由图9可知,锚周松砂位移场影响区的形状随着倾角的增加而改变。当θ=0°时,即垂直上拔状态下,位移影响区的形状为对称的贝壳形;当θ增至5°时,锚板上方位移影响区仍然为封闭的贝壳形,但整体形态不再对称而是偏向锚杆倾斜侧。当θ增至10°、20°时,位移影响区整体形状变化不大,仍然偏向锚杆倾斜侧,水平方向的位移也随着倾角的增大而增大。

图9 不同倾角下上拔承载力峰值时锚周松砂的位移场(H/D=5)

由前文3.2和3.3节倾角对上拔承载力的影响研究可知,在埋深较大时(H/D≥5),锚板倾角对上拔承载力的影响具有区间效应,当θ=10°左右时,上拔承载力最小。分析此现象的形成机理:上拔承载力的产生主要来自于松砂对锚板的作用力,倾角在0°～10°时,由图9可知,上拔力主要来自竖向松砂的作用,随着倾角的增大,松砂作用范围减小,因此上拔力随之减小;当倾角在10°～20°变化时,由图9可知,锚杆倾斜侧松砂的位移矢量大于锚板正上方松砂的位移矢量,表明侧向松砂的抗拔作用逐渐发挥并增大,因此锚板的上拔承载力逐渐增加。

4.2.2 倾斜角度对剪应变场的影响 图10为不同倾角上拔承载力峰值时锚周松砂的剪应变场(图中β1和β2为剪切破坏面与锚板的夹角)。由图10可以看出,锚板两侧的“剪应变泡”在锚板边缘斜上方由密到疏排列,且锚杆倾斜侧的“剪应变泡”更大一些。当θ=0°时,剪切破坏面从锚板边缘向内侧斜上方发展,呈现出截头圆锥形,剪切破坏面与锚板的夹角为68.0°;当θ=5°时,剪切破坏面依然从锚板边缘向内侧斜上方发展,但与锚板的夹角增大为84.4°和86.9°,此时剪切破坏面与锚板接近垂直;当θ增至10°时,剪切破坏面与锚板的夹角为78.7°和88.7°;当θ增至20°时,剪切破坏面与锚板的夹角为97.9°和81.2°,即锚杆倾斜反方向一侧的剪切破坏面向锚板边缘的外侧发展。

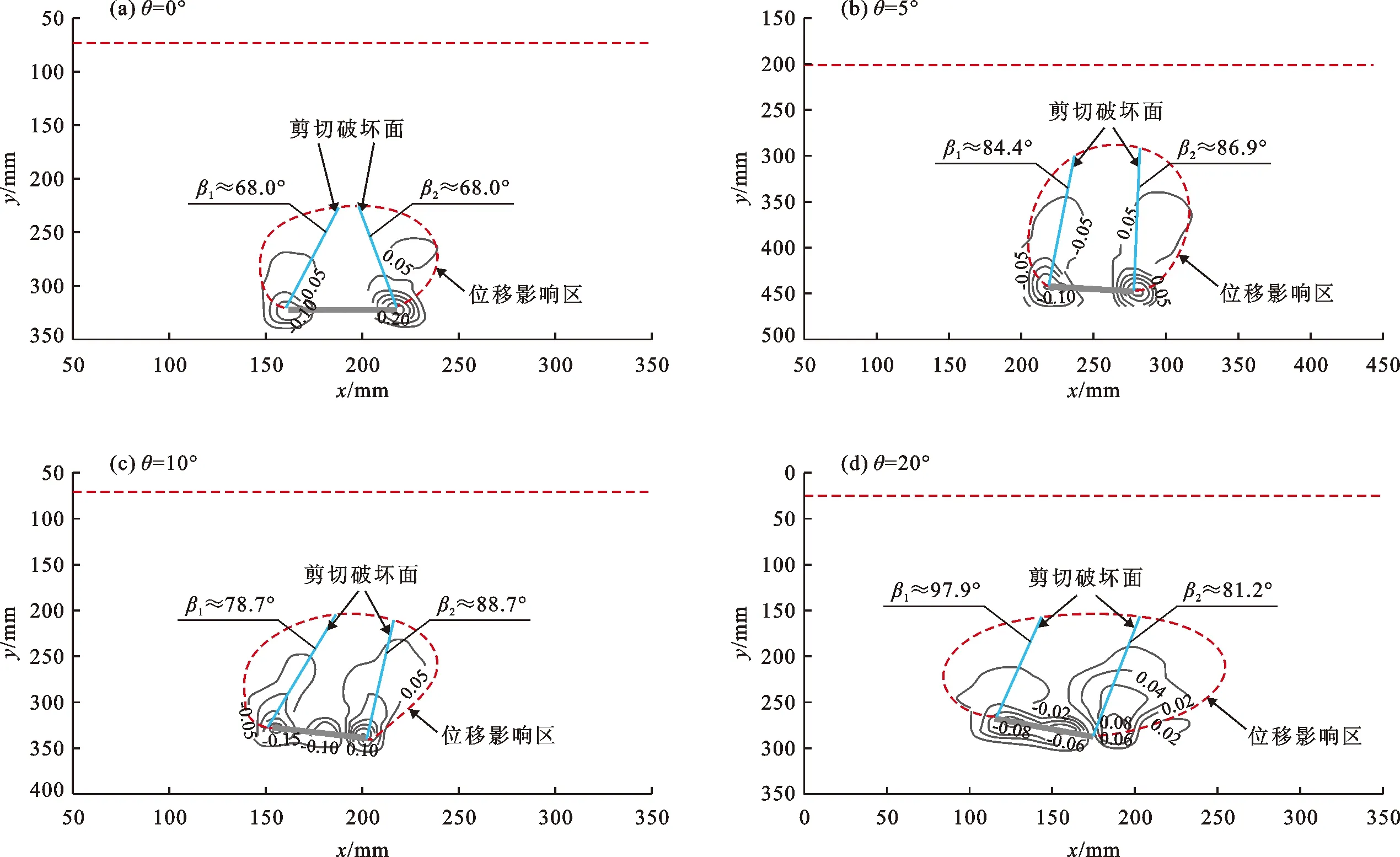
图10 不同倾角上拔承载力峰值时锚周松砂的剪应变场(H/D=5)

4.2.3 倾斜角度对体应变场的影响 图11为不同倾角上拔承载力峰值时锚周松砂的体应变场。由图11可看出,紧邻锚板周围为砂体体积膨胀区,且距锚板越近则体应变值越大。锚板倾角对松砂体积膨胀区的范围和最大体积膨胀量的影响并不显著,不同倾角下松砂体积膨胀区的范围均处在锚板上、下各(1/2)D的范围内。锚板上方出现砂体体积收缩区(θ=5°时出现在锚板左侧上方),且体积收缩区范围随着锚板倾角的增大而逐渐增大,但体积收缩量变化不大,基本维持在4%～5%范围内。上述结果说明锚板倾角的变化对锚板周围松砂体应变场的影响较小。

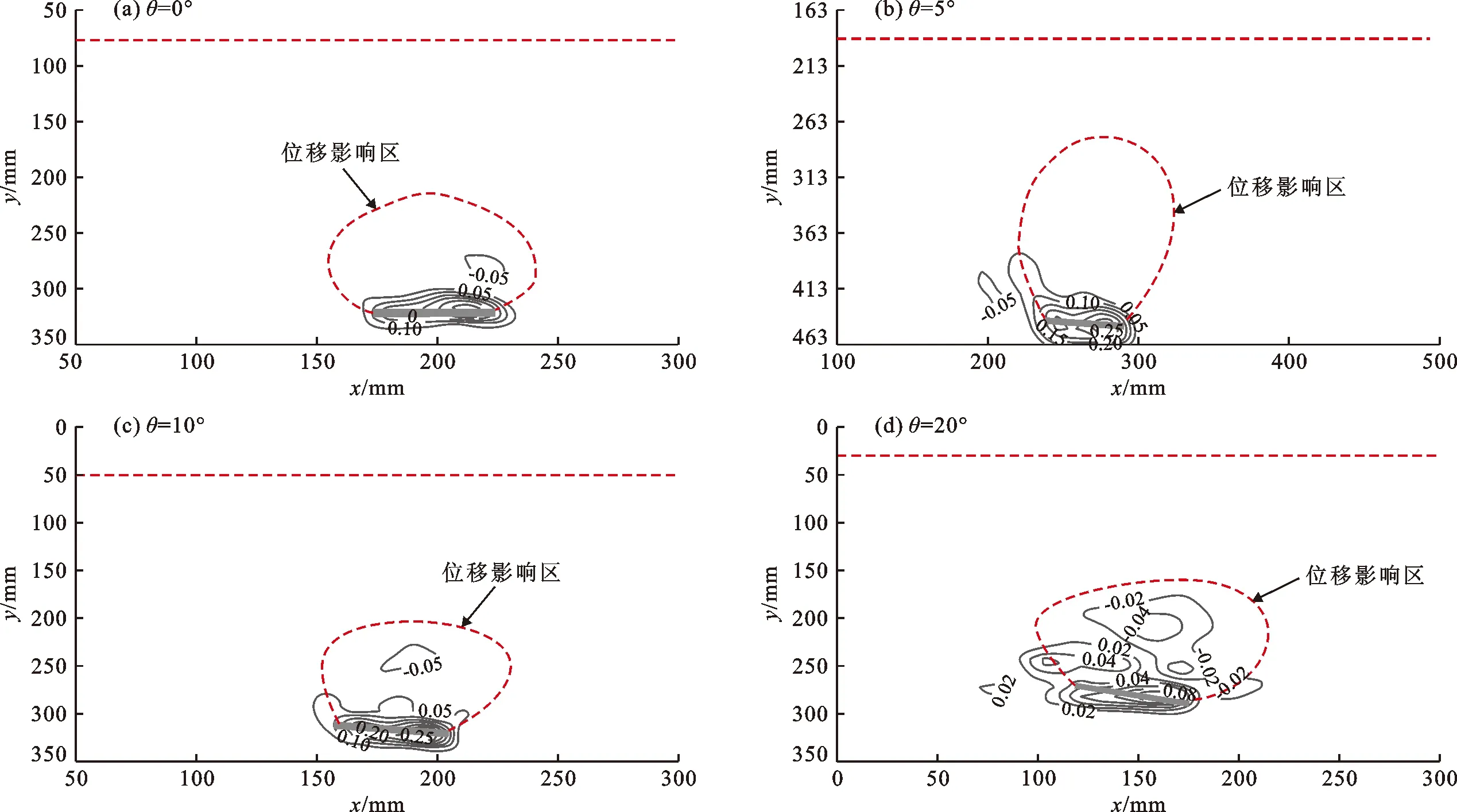
图11 不同倾角上拔承载力峰值时锚周松砂的体应变场(H/D=5)

5 讨 论

石恒俊等[12]也进行了砂土中锚板抗拔承载特性的室内模型试验研究,但其研究内容侧重于上拔承载特性的分析,而本文除了分析上拔承载特性外,还通过DIC技术获得了锚周松砂的位移场和应变场,进而详细分析了上拔松砂的变形特性。经过研究发现,倾斜锚板的上拔力峰值及上拔力峰值出现时的位移均随埋深比的增加而增大,这与文献[12]得到的结论相同。同时,本文还发现,倾角在0°～10°时,上拔力主要来自竖向砂体的作用;倾角在10°～20°时,侧向砂体的作用开始发挥并逐渐增大。该结论可为倾斜锚板工程的方案设计提供参考。

需要说明的是,由于DIC技术只能摄取模型箱侧壁表面砂体的变形信息,因而尚无法分析砂体内部更加完整的位移场和应变场。在今后的研究中,将尝试采用透明土模拟砂样的力学特性,采用多台相机获取三维图像,得到更加完整的砂样位移场和应变场信息,进一步提升对倾斜锚板上拔承载机理的认识。

6 结 论

本文以福建标准砂作为填料,开展了松砂中倾斜锚板的上拔承载特性模型试验,采用DIC技术对锚板周围松砂的上拔变形特性进行研究,重点分析了锚板的倾斜角度和埋深比对上拔承载力及松砂变形特性的影响,主要结论如下:

(1)当锚板倾角相同时,随着埋深比的增加,上拔力峰值Ff和相应的位移δf均逐渐增大;当锚板埋深比相同时,随着倾角的增加,上拔曲线发展形态基本一致,但埋深比会对此规律产生影响。在较大埋深比条件下(H/D=5,8),锚板倾角对上拔承载力的影响具有区间效应,即当倾角约为10°时,上拔极限承载力最小。

(2)当锚板在土体中呈倾斜状态上拔时,埋深比对锚板周围松砂有一定的影响。随着埋深比的增大,位移影响区的形状由延展至砂体表面的倒锥形逐渐转变为内置于土体的贝壳形,且位移矢量向锚杆倾斜侧集中,破坏模式也由整体破坏转变为局部破坏。锚板埋深比较小时,剪切破坏面沿锚板边缘向外延展;随着埋深比的增大,剪切破坏面转变为沿锚板边缘向内延展,且剪切破坏面与锚板的夹角逐渐增大,深埋时剪切破坏面与锚板接近垂直。松砂体积膨胀区围绕于锚板周围,体积收缩区处于锚板正上方,且随着埋深比的增加,最大体积膨胀量逐渐增大,最大体积收缩量变化不大。

(3)锚板倾角对松砂位移影响区的分布有一定影响,随着倾角的增大,位移影响区逐渐向锚杆倾斜侧集中,水平向的位移逐渐增加。当倾角在0°～10°时,上拔力主要来自竖向砂体的作用,随着倾角的增大,竖向砂体的调动范围减小,上拔力随之减小;当倾角在10°～20°时,侧向砂体的抗拔作用逐渐开始发挥并增大,因此锚板的上拔承载力逐渐增加,这也是锚板倾角对上拔承载力影响具有区间效应的内在机理。随着锚板倾角的增大,砂体剪切破坏面逐渐向两侧展开直至与锚板接近垂直。锚板周围存在体积膨胀区,且锚板倾角对体积膨胀区范围和最大体膨胀量的影响并不明显。随着倾角的增大,锚板上方出现体积收缩区,且体积收缩区范围随倾角的增大而增大。