部分冰盖下水流水力特性数值模拟

2023-09-11赖彦丞李映槿

水资源与水工程学报 2023年4期

陈刚, 金栋, 赖彦丞, 李映槿

(1.河海大学水文水资源与水利工程科学国家重点实验室, 江苏南京 210098; 2.云南省水利水电勘测设计研究院, 云南昆明 650021)

1 研究背景

河冰是陆地冰冻圈的重要组成部分[1],在其结冰-封冻-解冻周期性地生消演变中影响着水流流动边界[2],形成明流、完全冰封、部分冰封的不同流态[3-4]。封冻期水流表面被连续冰盖完全覆盖时,连续的附加无滑移边界主要在垂向上改变水流的运动规律,形成以最大流速点为界的两层结构[5-6];在结冰期和解冻期,水流表面一部分被冰覆盖,另一部分为自由水面,不连续的附加无滑移边界同时在横向和垂向上改变水流的运动规律,此时水流兼具明流水流和完全冰封水流的水力特性[7-8]。岸冰是部分冰盖的常见形式[9],按其形成时间和条件的不同,分为初生岸冰(结冰期)、固定岸冰(结冰期)、冲积岸冰(结冰期、融冰期)、再生岸冰(融冰期)、残余岸冰(融冰期)[10]。然而,相比明流和完全冰封水流,关于部分冰封水流水力特性的研究较少。水流流态在水力、热力的共同作用下急剧转变是冰凌致灾的主要原因,全面掌握包括部分冰封在内的所有流态的水力特性,才能更好地为寒区河流开发利用提供理论指导。

获取河冰生消演变对水流特性影响最直接的方法是开展原型观测,但在上游来水、河冰生消、河床演变的共同影响下,流动边界条件千差万别,原型观测得到的水流运动规律经验性较强,难以推广应用[11]。水槽试验能够直观地反映特定工况下水流流动特性,但是受限于断面测点布置和仪器量程,往往难以揭示整个流场的全部细节。数值计算可全面地反映所研究流场的各种细节,能获取许多原型观测和模型试验研究难以测量的数据,已被广泛应用于冰盖下水流结构的研究[12-13]。Lau等[14]通过建立k-ε湍流模型,研究了冰盖形成对水流垂向混合特性的影响;茅泽育等[15]采用k-ε湍流模型模拟冰盖下水流和物质输移的垂向二维分布,模拟结果表明连续冰盖下水流紊动黏滞系数并未出现零值点,水流纵向流速在流动核心区较为均匀,说明双对数律的假定存在问题;王军[16]采用标准k-ε湍流模型研究冰盖形成对水流流速分布的影响,通过模拟试验发现最大流速点的偏移范围有限;王志兴等[17]采用三维k-ε紊流模型模拟连续冰盖下水流纵向流速垂向分布,模拟结果表明双幂律待定参数的取值具有规律性;苏磊等[18]建立基于k-ε紊流模型的冰盖下水流垂向二维数值模型,探讨了连续冰盖下水流断面流速分布的主要影响因素。可见,现有研究多针对连续冰盖,而采用数值模拟方法研究部分冰盖下水流水力特性的成果还较少。

本研究采用Fluent软件建立部分冰盖下水流的数值模拟模型,并采用水槽试验数据对模型进行校验,从纵向流速分布、二次流结构、雷诺应力分布、紊动能分布等方面揭示部分冰盖下水流的水力特性。

2 数学模型

2.1 控制性方程

对于笛卡尔坐标系中的不可压缩流体的定常流动,紊流时均控制方程为[12]:

(1)

(2)

式中:ρ为流体的密度,kg/m3;u为雷诺平均流速,m/s;u′为脉动流速,m/s;p为压强,Pa;σij为应力张量分量,Pa; 下标i,j分别表示相应变量在xi,xj方向上的分量。

根据牛顿流体的应力-应变率本构关系,有:

(3)

式中:δij为Kronecker符号;μ为分子黏性系数,Pa·s; 下标l表示相应变量在xl方向上的分量。

由于控制性方程不封闭,因而在雷诺应力模型中引入雷诺输运方程、紊动能方程和紊动能耗散率方程使其封闭。紊动能和紊动能耗散率方程分别为:

(4)

(5)

式中:k为紊动能;ε为紊动能耗散率;Gk为紊动能生成项(剪切产生率);Cμ为无量纲常数(Cμ=0.09),Cε1和Cε2为源项中的经验常数,取Cε1=1.44,Cε2=1.92。

雷诺应力输运方程为[12]:

∏ij-Eij+Fij

(6)

(7)

(8)

(9)

(10)

(11)

(12)

式中:DT, ij为紊动扩散项;DL, ij为分子黏性引起的扩散项;Pij为应力产生项; ∏ij为压力应变项;Eij为黏性耗散项;Fij为系统旋转产生项。

2.2 边界条件

(1)进口边界条件:水流进口采用质量流进口边界,数值模拟与水槽试验相应工况的边界条件相同。进口边界的紊动能和紊动能耗散率分别采用公式(13)、(14)确定。

(13)

(14)

式中:I为紊动强度,结合试验得到的紊动强度分布规律参照Nezu等[19]的公式综合拟定;Cμ为常数,取Cμ=0.09;l为紊流特征尺度,l=0.07DH,其中DH为水力直径。

DH的计算公式为:

DH=4A/χ

(15)

(2)出口边界条件:采用压力出口边界。

(3)壁面边界条件:床面、边壁和冰盖均采用无滑移边界,近壁区采用标准壁面函数进行处理。床面和冰盖的阻力系数采用粗糙高度表示,两者的转换如公式(16)所示[20]。

(16)

式中:n1、n2分别为床面和冰盖的曼宁糙率系数,s·m-1/3;δ1、δ2分别为床面和冰盖的粗糙高度,m。

(4)对称边界条件:在对称边界上,垂直边界的速度取为0,其他物理量的值在对称边界内外相等。水面采用滑移壁面条件,即切应力为零。

2.3 计算工况

为便于采用水槽试验实测数据校验模型,数值模拟计算工况与水槽试验相同。试验在昆明理工大学水流与水工结构重点实验室的玻璃水槽试验系统中进行,玻璃水槽长度为15 m、宽度为0.8 m、高度为0.35 m,坡降固定为0.5‰,采用泡沫板制作模拟冰盖。试验时,采用矩形薄壁堰测量流量、水位测针测量断面水深、声学多普勒点式三维测速仪Vectrion测量流速。冰盖模拟为对称岸冰,以通过冰盖边缘的垂线为界,划分为被岸冰覆盖的冰盖区和表面为自由水面的明流区。定义冰盖覆盖度F为冰盖宽度与断面宽度的比值,即F=2b1/B(b1为单侧冰盖宽度;B为断面宽度),冰盖宽度b1依次取为0.10、0.15、0.20和0.30 m,相应的冰盖覆盖度F分别为0.250、0.375、0.500和0.750。为进行对比,增加冰盖覆盖F分别为0、1的特殊工况,分别对应明流工况和完全冰封工况,相应的冰盖宽度分别为0和0.40 m,数值计算工况见表1。测量时,每间隔5 cm布置1条垂线,依次记为Y05、Y10、Y15、Y20、Y25、Y30、Y35、Y40共8条垂线,每条垂线上布置10个测点。由于流场为对称分布,为节省计算资源,仅计算半宽区域,上游计算长度为断面宽度的4倍,下游计算长度为断面宽度的6倍。

2.4 方程离散与网格划分

采用计算流体软件Fluent进行计算,其控制方程的离散方法为有限体积法,选取二阶迎风格式作为空间离散格式,选取SIMPLEC(semi-implicit method for pressure linked equations consistent)算法处理压力与速度的耦合关系。计算区域采用笛卡尔坐标系,坐标原点设置在测量断面右侧,采用非均匀结构化网格进行划分,固壁(床面、边壁、冰盖)附近网格进行适当加密,计算网格为六面体结构化正交网格(图1)。经网格无关性检验,选取网格总数为3.6×106(60×60×1000)的非均匀网格。各方程的收敛控制精度均为1×10-5。

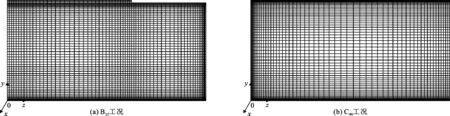
图1 模型计算网格划分示意图

2.5 模型校验

为了检验数值模型的可靠性,采用纵向流速的数值模拟结果与实测值进行对比。为便于作图,采用纵向时均流速垂向分布律对各垂线上的实测数据进行拟合。

无冰盖的明流工况O00采用单幂律拟合[21],其数学表达式为:

(17)

式中:umax为最大流速,m/s;H为水深,m;z为测点距床面的距离,m; 1/m为指数,其值与雷诺数有关。umax、m值可通过水槽试验实测资料拟合确定。

完全冰封工况采用双幂律进行拟合[22],其数学表达式为:

(18)

式中:k0为与流量有关的常数,m/s;m1,m2分别为与床面、冰盖粗糙高度有关的幂指数,可采用水槽试验实测数据拟合确定。

采用平均相对误差和拟合度指标评价理论公式性能。平均百分比误差(mean absolute percentage error,MAPE)为相对误差绝对值的算术平均值,其计算公式为:

(19)

式中:i为数据点数;N为数据量;us为模型模拟值;um为理论计算值。MAPE最小值为0,其值越小说明模型模拟值越接近参考数据。

拟合度指标是常用于判定非线性回归方程拟合度的统计参数,其计算公式为:

(20)

式中:FOI为拟合度指标,FOI最大值为1,其值越接近1说明模型模拟值与实测值的吻合程度越好。

各工况纵向时均流速模拟值与实测值对比见图2。通过计算得出各工况纵向时均流速的MAPE分别为4.16%、3.80%、2.57%、2.60%、4.00%和4.17%,FOI平均值分别为0.957 1、0.958 8、0.966 2、0.968 8、0.946 6和0.940 2,表明各工况的数值模型均得以校验。

3 结果分析与讨论

3.1 纵向时均流速分布

采用已校验的模型模拟各计算工况的纵向时均流速断面分布,如图3所示。在明流工况O00中(图3(a)),除近壁区流速较小外,在流核区流速相对均匀,模型验证结果表明纵向时均流速在水深方向上满足单幂律分布(图2(a)),最大流速位于自由水面附近。对于完全冰封C40工况(图3(f)),连续冰盖作为附加无滑移边界代替自由水面后,最大流速偏向断面中部,纵向时均流速在水深方向呈不对称“”型分布,可采用双幂律描述(图2(f))。对于部分冰封工况(图3(b)～3(e)),岸冰使得流速在断面上重新分配,总体上明流区流速增大,冰盖区流速减小,两者间存在明显的横向流速差。从图2、3可以看出,部分冰封工况的冰盖区流速垂向分布规律类似于完全冰封工况,可采用双幂律描述;明流区部分垂线流速分布类似于明流工况,可采用单幂律描述;在靠近冰盖边缘的区域存在过渡区,最大流速点偏向断面中部,纵向时均流速垂向分布规律不能采用单幂律描述,特别是冰盖覆盖度较大的工况,纵向时均流速在垂向上以不对称“”型分布为主,具有明显的二维特征。

图3 不同工况冰盖下水流纵向时均流速等值线断面分布

Peters等[3, 7]对不同宽度岸冰下水流流速分布的试验测量结果表明,明流区和冰盖区间存在过渡区,其流速垂向分布既不同于明流区的单幂律分布,也不同于冰盖区的双幂律分布。图3所示的模型模拟结果很好地展示了3种工况类型的水流纵向时均流速分布特性,特别是部分冰盖水流同时存在明流区、冰盖区和过渡区的二维特性。这表明采用的雷诺应力模型能够很好地模拟3种不同冰盖类型下水流的纵向时均流速分布特性。

3.2 二次流结构

图4给出了不同工况冰盖下二次流结构的模拟结果。图4(a)所示的明流工况O00断面上共有2个涡:底部涡A和表面涡B,以涡A为主,通过2个反向涡将流核区的高能流体带到边角区。随着冰盖覆盖度的增加,涡体形状、数量、大小和位置发生明显变化,流速等值线发生弯曲。对于B10工况(图4(b)),断面上共形成3个涡体,其中涡A和涡B为横跨冰盖区和明流区的反向涡体,以冰盖附近的涡B为主,将明流区的高能流量带至冰盖区,流速等值线凸向冰盖区,涡C作用较弱。对于B15工况(图4(c)),涡数量仍为3个,但冰盖附近的涡B主要位于冰盖区,以涡A为主,流速等值线凸向冰盖区。对于B20工况(图4(d)),冰盖附近的涡B完全位于岸冰下,并偏向冰盖边角,涡C逐步增强,位置偏向冰盖区和明流区交界的冰盖边缘附近。对于B30工况(图4(e)),涡B强度减弱,位于冰盖边角,并且在冰盖边缘处形成新的涡体D,此时以床面边角附近的涡A为主。对于C40工况(图4(f)),仅存在两个反向涡体,通过反向涡将流核区高能流体带至边壁附近。

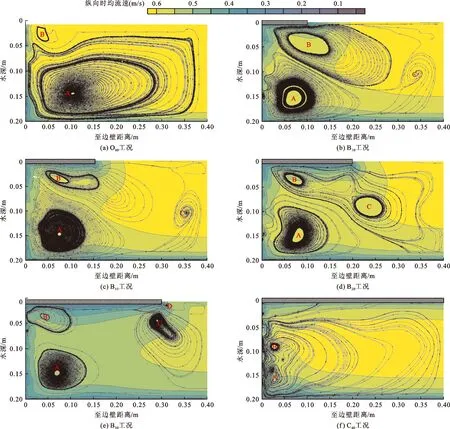
图4 不同工况冰盖下水流二次流结构

部分冰封B10、B15、B20和B30工况涡的数量均多于明流O00工况和完全冰封C40工况的,且涡体的大小、位置各不相同。这表明冰盖下水流二次流结构复杂,二次流结构随冰盖覆盖度的增大而变化;由于冰盖区流速小而明流区流速大,两者间存在横向流速梯度,通过二次流形成横向动量交换,这也验证了Peters等[3, 7]的试验测量结果。

3.3 雷诺应力分布

雷诺应力是流体质点脉动导致紊动微团在相邻流层间交换所产生的附加切应力。图5给出了不同工况冰盖下的雷诺应力的模拟值。

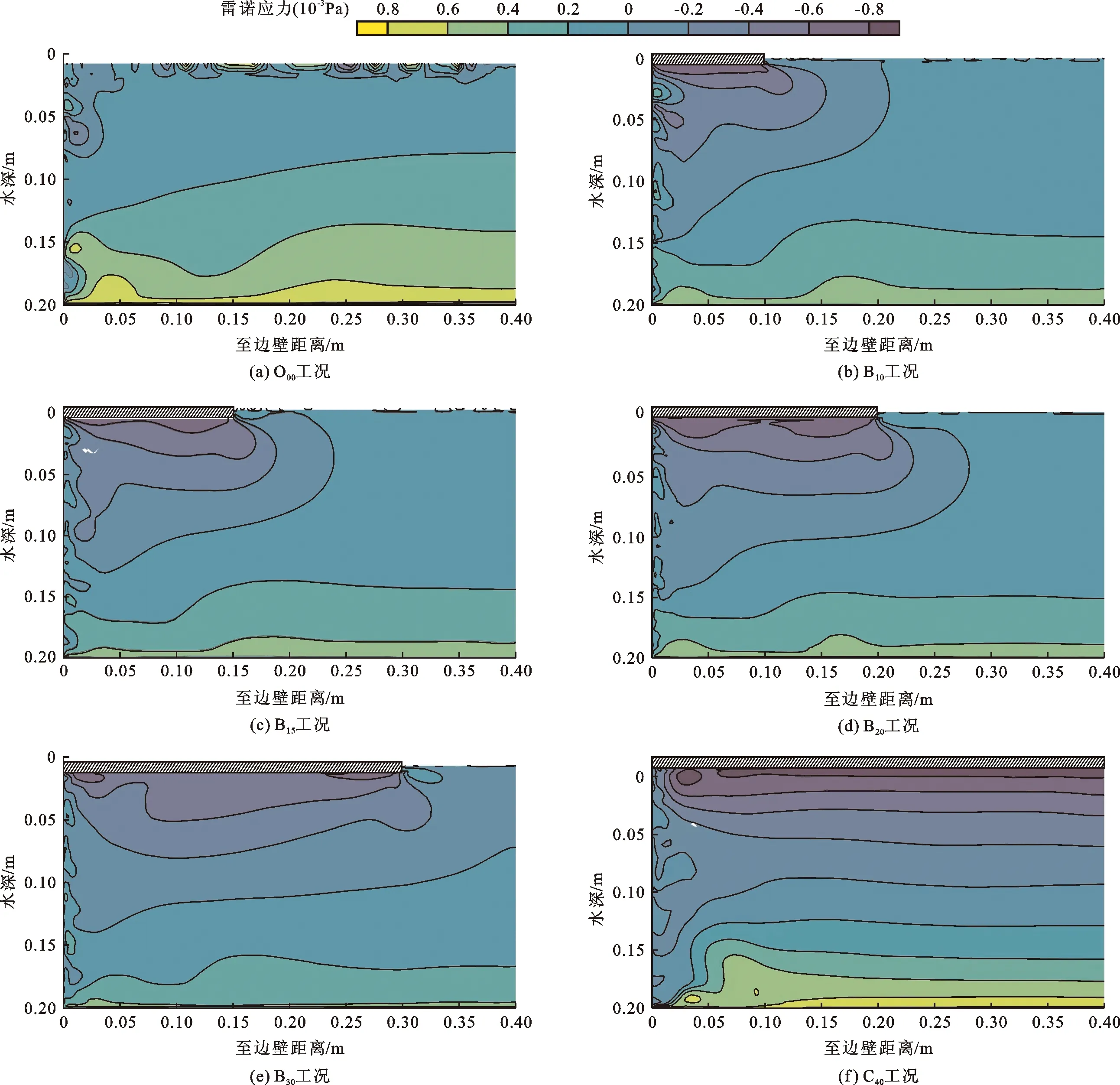
图5 不同工况冰盖下水流雷诺应力等值线分布

明流O00工况的雷诺应力最大值位于床面附近(图5(a)),随着距床面距离的增大而逐渐减小,总体符合线性分布。忽略宽浅断面中横向变化和二次流项,通过推导可得到明流雷诺应力的计算方法如公式(21)所示[23]。公式(21)表明紊流核心区雷诺应力在水深方向上呈线性分布,图5(a)所示的模型模拟结果与理论分析所揭示的规律相符。

(21)

式中:τxz为x-z平面上的切应力,Pa;τ01为床面切应力,Pa;H为水深,m;z为距床面的距离,m。

对于C40工况(图5(f)),雷诺应力在床面和冰盖附近取得极值,床面附近为正值,冰盖附近为负值,在水深方向上总体呈线性分布,零值点位于流核区。同理,推导得出的完全冰封水流雷诺应力计算方法如公式(22)所示[23]。公式(22)表明紊流核心区雷诺应力在水深方向上也呈线性分布,图5(f)所示的模型模拟结果与理论分析所揭示的规律相符。

(22)

式中:τ02为冰盖切应力,Pa。

对于部分冰封工况(图5(b)～5(e)),冰盖附近雷诺应力为负值,雷诺应力负值等值线凸向明流区,雷诺应力在断面上分布不均匀,随着冰盖覆盖度的增加,负值区范围逐步扩大,雷诺应力垂向分布不符合线性分布。这是因为水流横向动量交换较显著,使二次流项的影响不可忽略,从侧面反映了部分冰盖工况水流结构的复杂性。

3.4 紊动能分布

紊动能是常用于直观表征水流整体紊动状况的物理量。不同工况冰盖下水流紊动能的数值模拟结果见图6。明流O00工况(图6(a)),紊动能在固壁床面和边壁附近取得极值,这表明固壁附近瞬时流速在其均值附近较分散,反映出水体流速脉动在固壁附近较强[24]。对于完全冰封C40工况(图6(f)),紊动能在床面和冰盖附近取得最大值,流核区紊动最弱,紊动能大小与固壁的粗糙度有关,固壁越粗糙,紊动能越大。部分冰封工况的紊动能在断面上呈现明显的差异(图6(b)～6(e)),受床面、冰盖和边壁的共同影响,冰盖区紊动能明显大于明流区紊动能,紊动能等值线凸向冰盖区,明流区紊动能在床面附近取得最大值,在自由水面附近紊动最弱。对比部分冰盖B10、B15、B20和B30工况,岸冰替代部分自由水面成为附加的无滑移边界,水流流动阻力增大,横向流速差所产生的横向动量交换也会消耗水流的部分动能,使得水流的动能减小,这类似于复式断面明渠水流[4]。因此,在估算部分冰封断面过流能力时,应考虑横向动量交换的影响。