加筋土挡墙墙趾界面剪切刚度计算模型研究

张 琬, 陈建峰

(1.西安理工大学 土木建筑工程学院, 陕西 西安 710048; 2.同济大学 土木工程学院, 上海 200092)

1 研究背景

硬质墙面加筋土挡墙的面板通常不直接置于地基土之上,而是放置于混凝土制成的水平基座之上,并埋入地基中一定深度,形成了墙面-基座这一墙趾界面。墙趾界面上的摩擦阻力与筋材在墙面连接处的拉力共同平衡墙背水平土压力,起到约束墙面水平位移、减小筋材拉力的作用[1-2]。

实际工程中,墙趾界面的摩擦角和剪切刚度会因墙趾受到冲刷侵蚀或混凝土块体表面粗糙度的不同而发生改变,即墙趾约束条件发生改变[3-4]。墙趾约束条件对挡墙力学行为和稳定性有着不可忽视的影响。随着墙趾约束的减弱,墙面水平位移、筋材应变和筋材拉力均增大[5-9]。在墙趾周围地基失稳,即墙趾失去支撑的情况下,加筋土挡墙会发生组合式破坏[10]。Zhang等[11-12]通过离心模型试验和数值模拟揭示了墙趾约束机理:当水平基座埋置于地基土中时,由于基座前方的地基土抑制了基座-地基界面上剪切位移和剪应力的发展,故墙面-基座界面对挡墙起到主要的约束作用;当水平基座受到冲刷侵蚀等作用而裸露时,基座-地基界面起约束作用。鉴于墙趾约束作用对挡墙性状的显著影响,一些新的加筋土挡墙内部稳定性计算理论已将墙趾阻力涵盖其中[13-14]。

因此,在加筋土挡墙的数值模拟中,墙趾界面参数的选取对模拟结果的正确性至关重要。在岩土工程数值软件中(如PLAXIS、FLAC等),界面模型通常需要4个参数,即黏聚力、摩擦角、剪切刚度和法向刚度。由于混凝土界面无粘结,且在低应力水平下一般无法向变形,所以该界面黏聚力为0,法向刚度一般取1 000 MPa[15-16]。混凝土界面摩擦角可由大型界面剪切试验获取,也可通过较为简单的斜板试验获取,而剪切刚度值仅能通过界面剪切试验获取。学者们通过剪切试验研究了诸多类型界面(如混凝土界面、混凝土-土体界面、土工合成材料-土体界面等)的剪切特性,并尝试建立数学关系以描述界面的剪切行为[17-21]。但目前尚未有一种简单易用的混凝土界面剪切刚度的计算方法。

对此,本文对不同表面粗糙度的混凝土块体开展大型界面剪切试验,研究混凝土界面的剪切特性,构建界面剪切刚度与界面摩擦角、正应力的数学关系,提出墙趾界面剪切刚度的计算方法。将该计算方法应用于加筋土挡墙数值模拟中,为墙趾界面提供剪切刚度值,验证了该方法的正确性,并进一步讨论了墙趾约束条件对加筋土挡墙力学行为的影响。

2 混凝土界面剪切试验

2.1 试验方案

采用同济大学自主研制的大型结构面剪切试验机(SJW-200)对不同表面粗糙度的混凝土界面开展剪切试验。剪切盒尺寸为600 mm×400 mm×100 mm(长×宽×高)。试验机法向最大加载力为100 kN。由于墙面块体和水平基座多由素混凝土浇筑而成,故采用素混凝土块体作为试验材料。为了使不同方案混凝土界面的粗糙度相差较大,分别采用聚四氟乙烯膜和柔性土工膜对混凝土界面进行光滑处理,方法是将两块混凝土板相互接触的一面贴上聚四氟乙烯(polytetrafluoroethylene, PTFE)膜或柔性土工膜,形成天然和光滑处理后的3种不同粗糙程度的界面。

将2块尺寸与剪切盒匹配的素混凝土板分别放置于剪切试验机的上、下盒中,分别在40、80、120和160 kPa的正应力下,以1 mm/min的水平速度[22]对每个界面开展剪切试验。

2.2 试验结果

图1为天然混凝土界面的剪应力与剪切位移关系曲线;图2为3种混凝土界面抗剪强度包络线。由图1可见,在不同正应力(σn)下,随着剪切位移的增加,界面剪应力快速增大,达到峰值后,剪应力基本保持稳定。随着界面正应力的增加,界面峰值剪应力增大。图2显示天然混凝土界面的摩擦角为39°,似黏聚力为1 kPa。

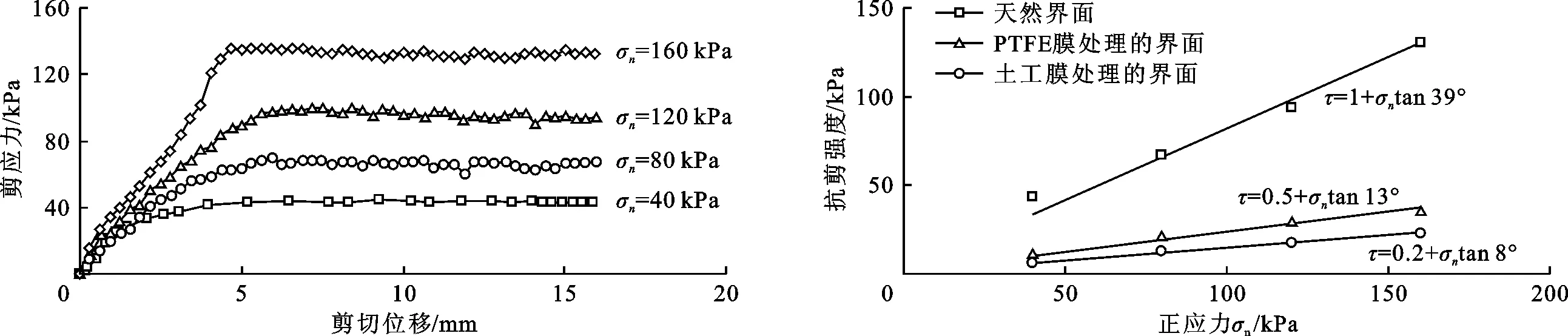
图1 不同正应力下天然混凝土界面剪应力-剪切位移曲线 图2 3种混凝土界面抗剪强度包络线

图3和4分别为不同正压力下采用PTFE膜处理和柔性土工膜处理的混凝土界面的剪应力与剪切位移关系曲线。

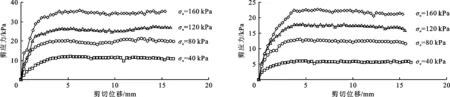
图3 PTFE膜处理的混凝土界面剪应力-剪切位移曲线 图4 柔性土工膜处理的混凝土界面剪应力-剪切位移曲线

由图3可见,混凝土界面经PTEE膜光滑处理后,剪应力仍随剪切位移的增加而快速增大,达到峰值后变化较小。由图2中该界面的抗剪强度包络线可见,与天然混凝土界面相比,该界面抗剪强度显著减小,比如,在160 kPa的正应力下,天然混凝土界面抗剪强度为136 kPa,而该界面抗剪强度减小至35 kPa。对混凝土界面采用PTFE膜处理后,界面摩擦角为13°,似黏聚力为0.5 kPa(图2)。界面摩擦角不为0表明界面并非完全光滑。界面摩擦角的正切值为界面摩擦系数,经PTFE膜处理后,混凝土界面的摩擦系数由天然界面的0.81减小至0.23,即其摩擦系数减小至天然工况的约1/4。

由图4可见,随着剪切位移的增加,土工膜处理的混凝土界面剪应力增长较为缓慢,这同土与混凝土界面剪应力的增长规律一致[18]。然而,不同于土-混凝土界面的是,该界面剪应力峰值清晰,这应是混凝土界面刚度较大造成的。图2中土工膜处理的混凝土界面的抗剪强度包络线显示,与天然界面和采用PTFE膜处理的界面相比,该界面抗剪强度显著减小,比如,在160 kPa的正应力下,天然界面和PTFE膜界面的抗剪强度分别为136和35 kPa,该界面抗剪强度减小至23 kPa。对混凝土界面采用柔性土工膜处理后,界面摩擦角为8°,界面似黏聚力为0.2 kPa(图2),界面摩擦系数由天然界面的0.81减小至0.14,即其摩擦系数减小至天然工况的约1/6。

3 墙趾界面剪切刚度计算模型

图5为上述3种混凝土界面的剪切刚度与正应力关系曲线。Bathurst等[22]建议选取剪切位移为2 mm时的剪应力与剪切位移之比作为混凝土界面的剪切刚度值,本文也采用此方法确定界面剪切刚度值。由图5可见,各种界面剪切刚度均随正应力的增加而增大。在同一正应力下,土工膜处理的界面(摩擦角8°)、PTFE膜处理的界面(摩擦角13°)和天然界面(摩擦角39°)的剪切刚度依次增大,可见混凝土界面剪切刚度与界面摩擦角和正应力均呈正相关关系。

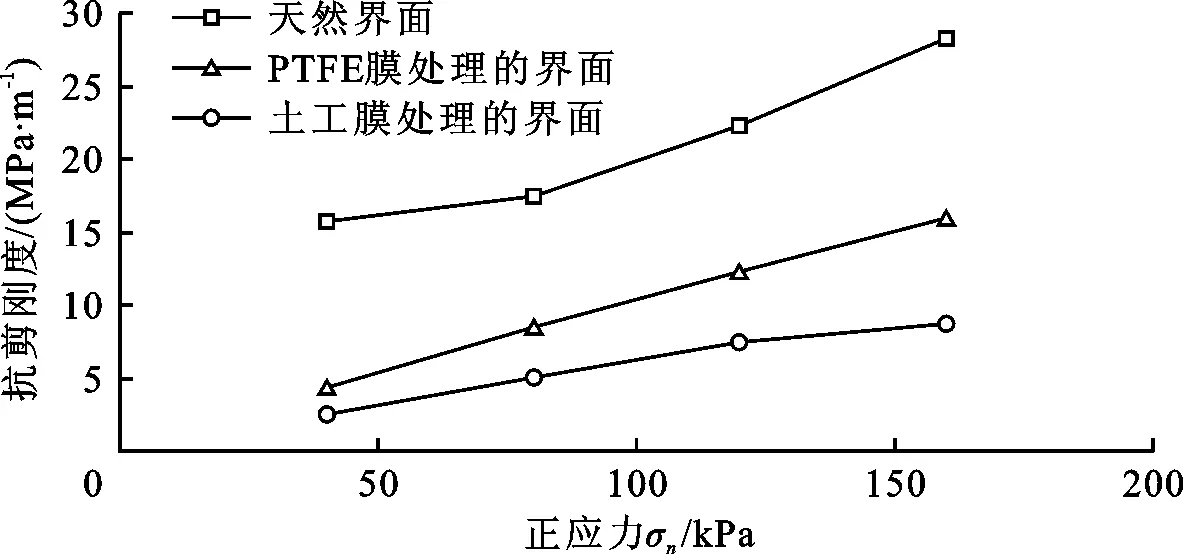
图5 3种混凝土界面剪切刚度-正应力曲线

在加筋土挡墙中,墙趾界面正应力σn由挡墙高度H决定,σn与H的关系为:

σn=H·γb

(1)

式中:H为挡墙高度,m;γb为混凝土墙面重度,kN/m3。

在实际工程中,挡墙高度是确定的,墙趾界面摩擦角可通过简单的混凝土斜板试验获得,而界面剪切刚度不易直接测得,鉴于这种情况,可采用本文界面剪切试验获得的混凝土界面剪切刚度与界面摩擦角及正应力的对应关系,建立墙趾界面的剪切刚度计算模型。

将3种不同粗糙度的混凝土界面在不同正应力下的剪切刚度绘制于图6(a)中,以获得墙趾界面剪切刚度与界面摩擦角和正应力的关系,其关系式可用对数函数表示为:

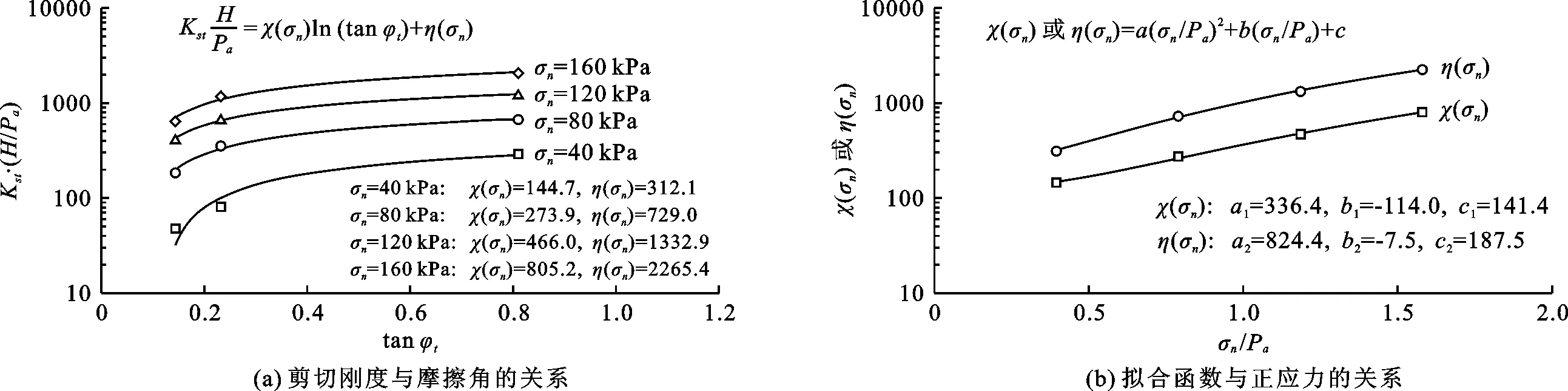
图6 墙趾界面剪切刚度与摩擦角及正应力的关系曲线

(2)

式中:Kst为混凝土界面剪切刚度,用H和Pa对其作了无量纲处理;H为墙面高度,m,与墙趾界面正应力的关系为H=σn/γb;Pa为标准大气压(101.3 kPa);χ(σn)、η(σn)为拟合函数;φt为墙趾界面摩擦角,(°)。

由图6(a)可见,χ(σn)、η(σn)的值均随σn的增加而增大。将不同σn对应的χ(σn)、η(σn)的值绘制于图6(b)中,并用多项式函数表示其关系:

(3)

(4)

式中:用标准大气压Pa将σn无量纲化;a1、a2、b1、b2、c1、c2均为拟合系数,其值如图6(b)所示。

上述关系式(2)～(4)则为墙趾界面剪切刚度计算模型,该计算模型的输入参数为墙趾界面正应力和摩擦角。

已知σn与H的关系式,以及素混凝土块的密度一般为2 200 kg/m3,即混凝土墙面的重度为21.6 kN/m3,可建立墙趾界面剪切刚度Kst与墙高H、墙趾界面摩擦角φt的一一对应关系,如图7所示。图7中给出了φt在5°至45°范围内、H=3～10 m范围内的Kst值,超出此范围的Kst值可由关系式(2)～(4)计算得出。由图7可见,墙趾界面剪切刚度随界面摩擦角或墙高的增大而增大。随着界面摩擦角的增大,剪切刚度增大速度加快,而随着墙高的增大,剪切刚度增大的速率较为稳定。

图7 墙趾界面剪切刚度Kst与H、φt的对应关系(Kst单位:MPa/m)

4 墙趾界面剪切刚度计算模型验证

4.1 原型加筋土挡墙

以文献[8]中的3组离心模型试验挡墙为原型,该3组离心模型挡墙(记为M1～M3)的尺寸和材料相同。墙高为180 mm,墙面仰角为8°,筋材长140 mm,筋材间距为30 mm。填土和地基土采用中砂,压实度分别为95%和97%,对应的密度分别为1.57和1.62 g/cm3,摩擦角分为36°和38°。筋材采用尼龙灰窗纱,抗拉强度为2.5 kN/m,5%伸长率下的刚度为18 kN/m。墙面模块和水平基座采用素混凝土块,墙面模块间有凹凸槽连接。采用应变片测量筋材应变。各离心模型加速度均由0匀速增加到20g,在20g加速度下读取各测量元件的数据。M1～M3唯一的不同之处在于墙趾界面的粗糙程度,墙趾界面摩擦角分别为39°、13°和8°。

4.2 数值模型

采用FLAC有限差分程序建立加筋土挡墙数值模型,数值模型按照相似原理还原为原型尺寸建立,如图8所示。各数值挡墙的填土和地基土均采用莫尔-库仑模型,墙面模块采用线弹性模型,筋材采用Cable单元,混凝土块体之间以及混凝土与土体之间设置接触面单元,各材料参数取值如表1所示。

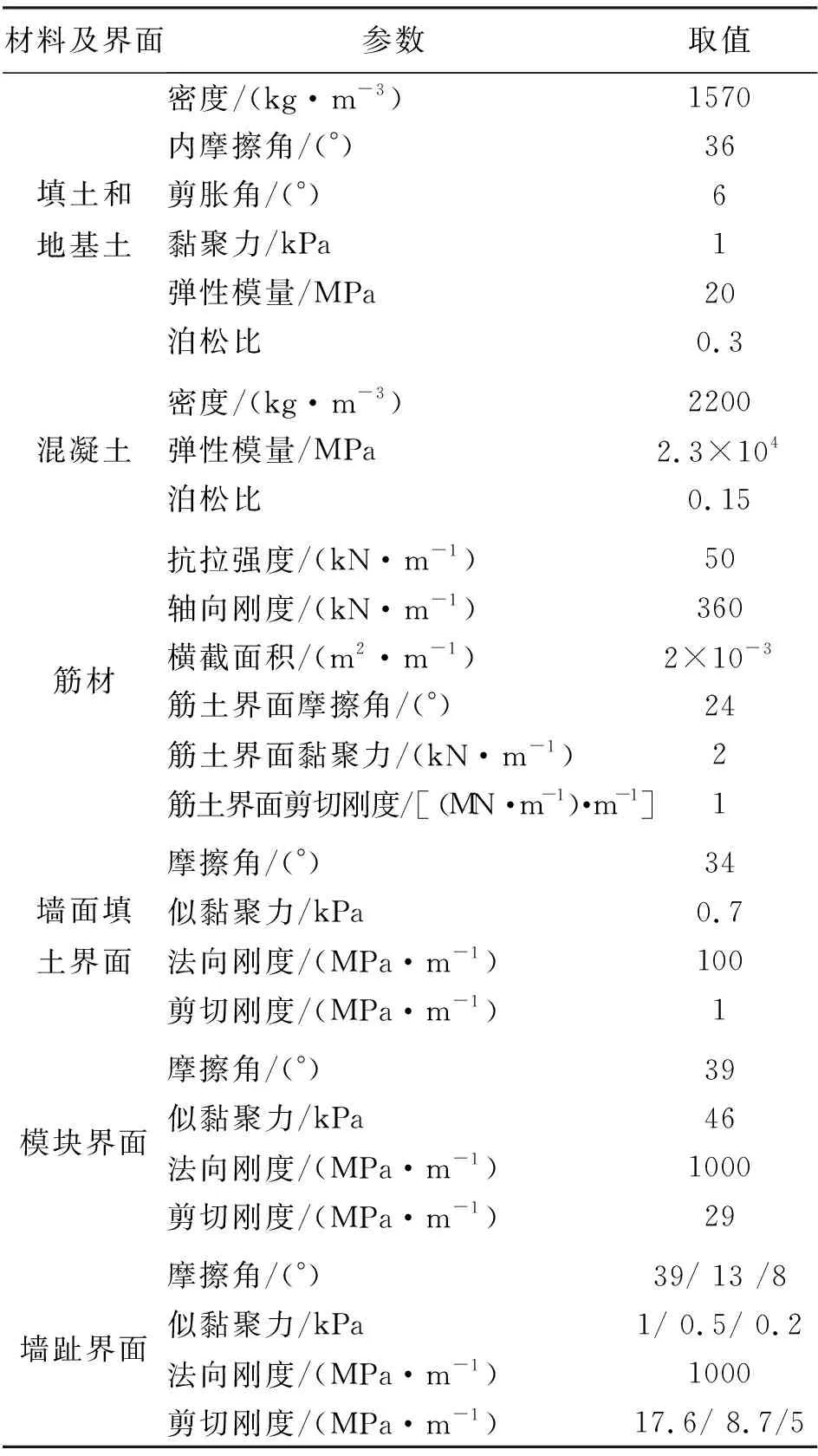
表1 数值模型各材料参数取值

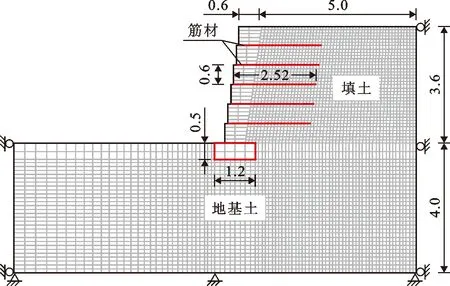
图8 加筋土挡墙数值模型(单位:m)

因数值模型为原型尺寸,其材料参数也按照相似关系还原为原型取值。为了方便计算,填土与地基土取相同的参数值。筋土界面似黏聚力、摩擦角和剪切刚度由尼龙灰窗纱的拉拔试验结果确定。土-混凝土界面、墙面模块界面参数值参照Yu等[16]在模块式加筋土挡墙数值模拟中的参数取值。墙趾界面剪切刚度根据墙高和墙趾界面摩擦角在图7中选取相应的值。

各挡墙模型建立的过程为:首先在地基中的水平基座上生成第一层墙面模块;再生成模块对应高度的填土,并设置相关的接触面单元;对填土表面施加8 kPa竖直向下的均布荷载以模拟实际挡墙建造过程中对填土的压实;而后生成筋材单元;如此往复,直至挡墙填筑至预定高度。

4.3 结果分析与讨论

图9为3组挡墙实测和数值计算的各层筋材应变。由图9可见,3组挡墙中,数值计算的各层筋材应变沿筋材长度的分布规律以及应变值均与实测结果接近。实测的筋材应变普遍大于计算值,这是因为试验中仅在筋材的上表面粘贴了应变片,并不是在筋材上下表面粘贴一对应变片,使得测试数据中无法消除筋材弯曲引起的应变[12],而数值计算值仅为轴向应变,因而导致实测值大于计算值,尤其是在填土变形较大的墙面与筋材连接的位置,实测值偏大更为明显。由图9还可以看出,M1～M3挡墙墙趾界面的摩擦角依次减小,筋材应变峰值依次增大,在挡墙中下部筋材中该趋势尤为明显。这是因为墙趾约束作用减弱,导致挡墙中下部发生较大变形,从而激发了筋土间摩擦,筋材应变增大。

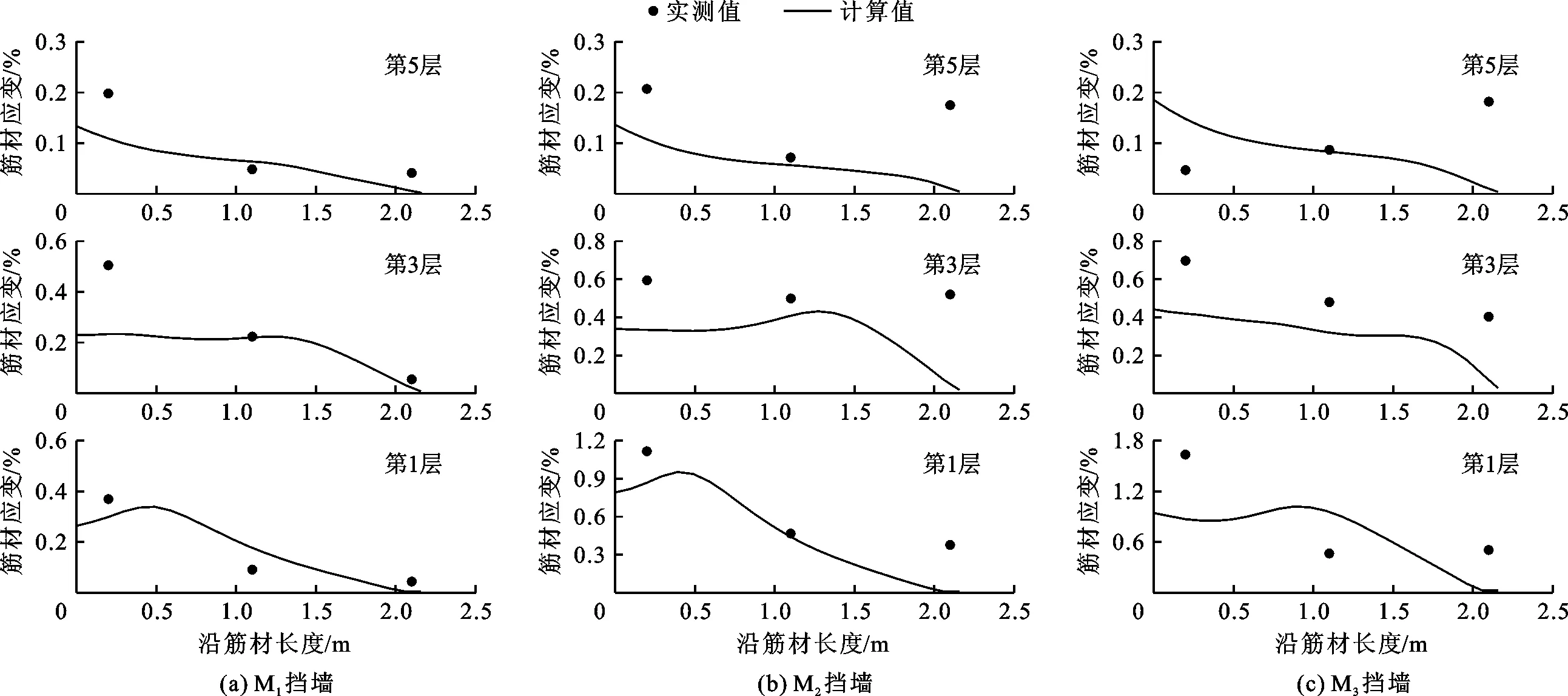
图9 3组挡墙(M1～M3)各层筋材应变的实测值与数值计算值比较

在M2和M3挡墙的第1、3层筋材中,应变在筋材中后段有一处明显峰值,这说明M2、M3挡墙填土中已出现连贯的剪切带。图10给出了M1～M3挡墙的填土剪应变云图,为使挡墙轮廓更为清晰,在剪应变云图中仅显示填土和地基土的网格。由图10可见,M1的填土最大应变不超过2%,且填土最大应变发生于各层筋材连接处和墙趾处。由于M2和M3的墙趾界面摩擦角和剪切刚度减小,该两挡墙中下部填土产生了较大的剪切应变,M2的土体最大应变超过4%,位于底层模块后方,M3的土体最大应变超过3%,位于水平基座后方。砂土的平面应变剪切试验结果表明,砂土峰值剪切应变为2%～3%[23],这说明M2和M3两挡墙的填土已发生了局部破坏。

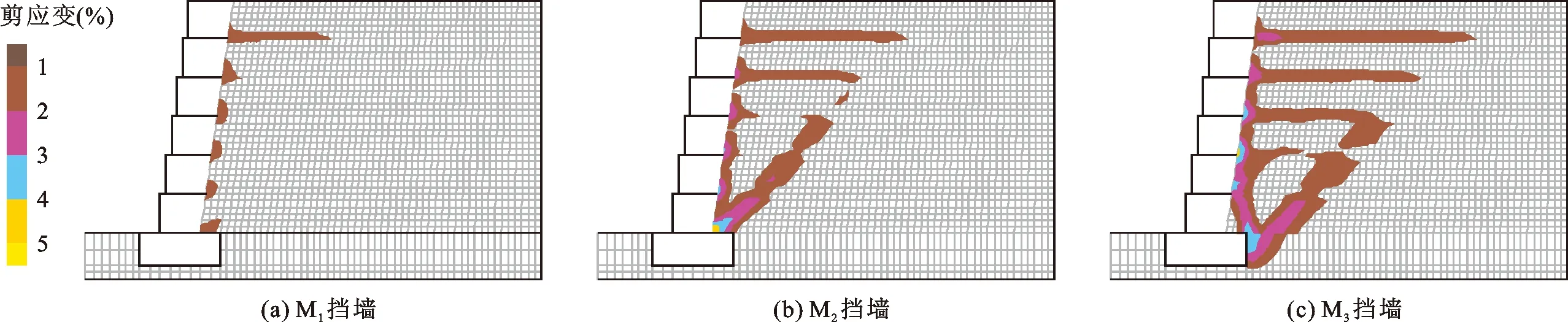
图10 3组挡墙(M1～M3)填土剪应变云图

图11为3组挡墙筋材最大拉力的数值计算值,图中还给出了K-刚度法[13]和现行规范法[24]的计算值作为对比。由图11可见,对于墙趾正常约束的挡墙(M1),其筋材拉力与K-刚度法的计算值较为接近,远小于规范法的计算值,数值计算得出的筋材拉力沿墙高呈现中间大、顶底部小的“鼓肚”状分布。由图10可知,M1挡墙处于正常工作状态,而K-刚度法正是一种针对工作应力状态下加筋土挡墙的设计方法。因此,对于墙趾正常约束的加筋土挡墙,宜采用K-刚度法进行内部稳定设计。对于墙趾约束作用减弱的挡墙(M2、M3),K-刚度法严重低估了其中下部的筋材拉力,而现行规范法高估了筋材拉力,数值计算得出筋材拉力沿墙高呈现顶部小、底部大的三角形分布,与规范法计算值的分布形态一致。建造在山区、河岸的加筋土挡墙,其在服役过程中易因趾部受到冲刷侵蚀而失去墙趾约束[3-4],因此,这类挡墙宜采用现行规范法进行设计。随着墙趾约束作用的减弱,筋材拉力沿墙高的分布形态由“鼓肚”状向三角形转变,这一现象与已有的加筋土挡墙模型试验结果一致[10-11]。

图11 3组挡墙(M1～M3)筋材最大拉力沿墙高分布曲线

综上,在加筋土挡墙数值模拟中采用本文提出的墙趾界面剪切刚度计算模型选取墙趾界面参数,所得筋材变形和受力均与模型试验结果吻合,验证了该计算模型的合理性。

5 结 论

本文对不同粗糙程度的混凝土界面开展大型剪切试验,研究混凝土界面剪切特性,在此基础上,提出墙趾界面剪切刚度计算模型,并将该计算模型应用到加筋土挡墙的数值模拟中,验证该模型的可行性。得到如下结论:

(1)墙趾界面的剪切刚度与界面摩擦角、正应力均呈正相关关系。

(2)本文提出的墙趾界面剪切刚度计算模型的输入参数为墙高和墙趾界面摩擦角,其中界面摩擦角可通过简单的混凝土斜板试验获得。

(3)采用墙趾界面剪切刚度计算模型为3组不同墙趾约束条件的加筋土挡墙数值模型提供墙趾界面剪切刚度值,各挡墙筋材应变的数值计算值均与实测值吻合较好。筋材拉力计算值沿墙高的分布形态随着墙趾约束作用的减弱,由中部大、顶底部小的“鼓肚”状向顶部小、底部大的三角形转变,这与已有的加筋土挡墙模型试验结果一致。

(4)数值模拟结果证明了墙趾界面剪切刚度计算模型的合理性。该计算模型作为一种无需试验即可获取混凝土界面剪切刚度的简便工具,也可为其他工程(如混凝土坝、建筑结构)中存在的混凝土界面提供剪切刚度值。