基于数据处理与若干群体算法优化的GRU/LSTM水质时间序列预测

杨坪宏, 胡 奥, 崔东文, 杨 杰

(1.云南省水文水资源局, 云南 昆明 650106; 2.临沧润汀水资源科技服务有限公司,云南 临沧 677000; 3.云南省文山州水务局, 云南 文山 663000; 4.北京全路通信信号研究设计院集团有限公司昆明分公司, 云南 昆明 650041)

1 研究背景

提高水质时间序列预测精度对于水环境治理和水生态保护具有重要意义[1]。当前,除MIKE 21等水质模拟模型外,有关水质预测的方法可分为3类。第1类是以逐步回归为代表的传统预测方法;第2类是以机器学习为代表的预测方法,如BP(back propagation)神经网络[2-3]、支持向量回归机[4]、长短期记忆神经网络(long short-term memory networks,LSTM)[5-6]、非线性自回归神经网络[7]等,此类方法提高了对非线性问题的处理能力,但权值阈值或关键参数的合理选取制约了其预测精度的提升,目前普遍采用群体智能算法进行寻优,并获得较好的预测效果。第3类是组合预测法,组合预测法分两种方式,一种是基于两个或两个以上预测器的组合预测,如TimeGAN-CNN(convolutional neural networks)-LSTM模型[8]、GRNN(general regression neural network)-Markov模型[9]、STG(spatial-temporal graph)-LSTM模型[10]等,组合预测方法的特点是利用各模型的优势来克服单一预测模型的不足,但预测结果往往存在较大的不确定性;另一种是基于信号分解技术的预测方法,该方法利用分解技术将时序数据分解为若干更具规律的子序列分量,通过对子序列分量进行预测、重构后得到最终预测结果。由于基于信号分解技术的预测方法具有较好的预测精度,该方法已在水质时间序列预测研究中得到广泛应用,如孙铭等[11]提出的小波分解-长短期记忆网络(W-LSTM)时间序列预测模型;金昌盛等[12]提出的奇异谱分析-遗传算法-BP神经网络(SSA-GA-BP)预测模型;顾乾晖等[13]提出的变分模态分解-粒子群优化算法-长短期记忆神经网络(VMD-PSO-LSTM)预测模型;李建文等[14]提出的集合经验模态分解-支持向量回归机(EEMD-SVR)预测模型;白雯睿等[15]提出的变分模态分解-卷积神经网络-长短期记忆神经网络(VMD-CNN-LSTM)组合水质预测模型。

近年来,随着大数据和人工智能的发展,LSTM、门控循环单元(gated recurrent unit,GRU)已被应用于水质预测[15-16]的研究中。LSTM是循环神经网络(recurrent neural network,RNN)的变种,其克服了RNN面临的梯度消失和梯度爆炸问题 ,在问题分类[17]、预测研究[18-21]等领域应用广泛。GRU是LSTM的变种,与LSTM相比,GRU拥有更低的复杂度以及更好的预测性能,被应用于各类预测研究[22-24]之中。在实际应用中,GRU/LSTM超参数(包括层数、学习率、隐含层节点数、dropout、LearnRateDropPeriod等)对GRU/LSTM预测性能具有较大影响,需要通过人工不断调整试错得到GRU/LSTM超参数,不仅要求操作人员具有丰富的调参经验,而且极易陷入局部极值,难以满足GRU/LSTM的预测需求。目前,海洋捕食者算法[18]、粒子群优化算法等[25-28]群体智能算法(swarm intelligence algorithms,SIA)已在寻优GRU/LSTM超参数中得到应用,并取得了较好的调优效果。

为提高pH值及CODMn、DO、NH3—N浓度时间序列的预测精度,改进GRU/LSTM的预测性能,拓展SIA在GRU/LSTM超参数调优中的应用范畴,本文基于小波包变换(wavelet packet transform,WPT)分解技术和“分解算法+智能算法+预测模型+叠加重构”思想,研究提出采用变色龙优化算法(chameleon swarm algorithm,CSA)、猎豹优化(cheetah optimization,CO)算法、山瞪羚优化(mountain gazelle optimization,MGO)算法分别调优GRU/LSTM超参数的水质时间序列预测模型,并构建WPT-GRU、WPT-LSTM模型及基于SVM预测器的WPT-CSA-SVM、WPT-CO-SVM、WPT-MGO-SVM模型进行对比分析,然后通过云南省昆明市观音山断面pH值、DO、CODMn、NH3—N预测实例对各模型进行检验。

2 数据来源与研究方法

2.1 数据来源

本文以云南省昆明市观音山断面2004—2015年逐周pH值及CODMn、DO、NH3—N浓度时间序列预测为例对各模型进行验证。原始pH值及CODMn、DO、NH3—N浓度数据来源于原环境保护部数据中心的水质周报,共624组,对于个别缺失数据采用线性法进行插补,昆明市观音山断面水质时间序列3D图见图1。从图1可以看出,该断面水质pH值及CODMn、DO、NH3—N浓度时序数据呈现出非线性、多尺度等特征,起伏变化激烈。

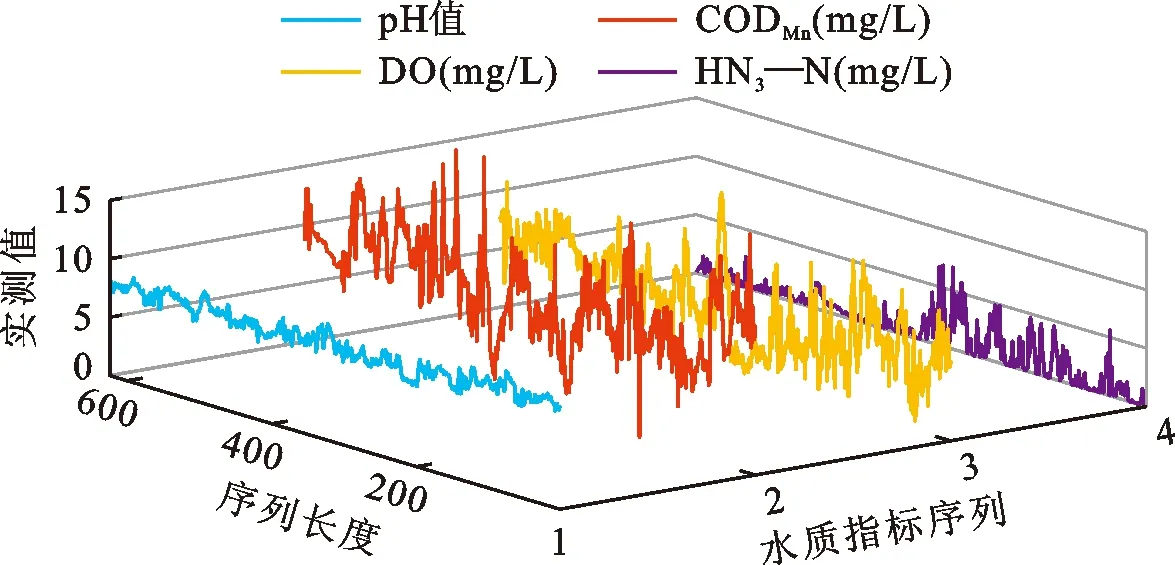
图1 昆明市观音山断面水质时间序列3D图

2.2 研究方法

2.2.1 小波包变换(WPT) WPT能同时对信号低频部分和高频部分进行分解,更适用于水质时间序列分解。WPT对pH值及CODMn、DO、NH3—N浓度原始信号进行分解的公式为[29-32]:

(1)

重构算法为:

(2)

式中各参数意义见文献[32]。

2.2.2 变色龙优化算法(CSA) CSA是Malik等于2021年提出的一种新型智能优化算法,该算法通过对变色龙搜索猎物、锁定猎物、攻击猎物3种行为进行数学建模来求解待优化问题[33-34],CSA数学描述具体见文献[34]。

2.2.3 猎豹优化(CO)算法 CO算法是Akbari等[35]于2022年受自然界猎豹狩猎启发而提出的一种新型智能优化算法。该算法通过模拟猎豹在狩猎过程中搜索、坐等和攻击3种策略来实现位置更新,即待优化问题的求解。CO算法数学描述如下:

(1)初始化。与其他群体智能优化算法类似,CO算法也是从种群初始化开始。设在d维搜索空间中,猎豹初始化位置描述为:

Xi,j=LBj+rand·(UBj-LBj)

(3)

(i=1,2,…,n;j=1,2,…,d)

式中:Xi,j为第i头猎豹第j维位置;UBj、LBj为第j维搜索空间上、下限值;rand为介于0和1之间的随机数;n为猎豹种群规模;d为问题维度。

(2)搜索策略。猎豹在其领地(搜索空间)或周围区域进行全范围扫描或主动搜索,以找到猎物。该策略数学描述为:

(4)

(3)坐等策略。在搜索模式下,猎物可能会暴露在猎豹视野中,在这种情况下,猎豹的每一个动作都可能会导致猎物逃跑。为避免该情况发生,猎豹采取坐等伏击策略(躺在地上或躲进灌木丛)以接近猎物。该策略数学描述为:

(5)

该策略不但可提高狩猎成功率(获得最优解),而且还避免了CO过早收敛。

(4)攻击策略。在CO算法中,种群中每头猎豹都可以根据逃跑猎物、领头猎豹或附近猎豹的位置来调整自己的位置,以获得最佳攻击位置。该策略数学描述为:

(6)

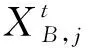
2.2.4 山瞪羚优化(MGO)算法 MGO是Abodollahzadeh等[36]于2022年受自然界中瞪羚生存能力启发而提出的一种新型群体智能优化算法。该算法通过对瞪羚觅食(开发阶段,在没有捕食者或在捕食者跟踪情形下)、逃离(探索阶段,发现捕食者)行为进行数学建模求解待优化问题。MGO算法数学描述如下:

(1)初始化。与其他群体智能优化算法类似,MGO也是从种群初始化开始。设在d维搜索空间中,瞪羚种群为N的个体初始化位置描述为:

xi,j=LBj+rand·(UBj-LBj)

(7)

(i=1,2,…,N;j=1,2,…,d)

式中:xi, j为第i只瞪羚第j维位置;UBj、LBj为第j维搜索空间上、下限值;rand为介于0和1之间的随机数;N为瞪羚种群规模;d为问题维度。

(2)觅食(开发)阶段。MGO中,假设在没有捕食者或在捕食者跟踪情形下,瞪羚悠闲地觅食,并在觅食时以布朗运动进行移动,瞪羚位置更新数学描述为:

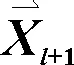
(8)

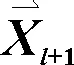
(3)逃离(探索)阶段。MGO中,瞪羚一旦发现捕食者就迅速奔跑,并通过快速奔跑和突然改变方向来逃离捕食者。假设瞪羚起步阶段采用布朗运动,奔跑阶段改用Lévy飞行。瞪羚发现捕食者时,其位置更新描述为:

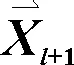
(9)

捕食者追逐瞪羚时,其位置更新描述为:

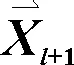
(10)

式中:CF为捕食者移动的控制参数,描述为CF=(1-l/T)(2l/T);l为当前迭代次数;T为最大迭代次数;其他参数意义同上。

(4)捕食成功率。研究表明,虽然瞪羚不是濒危物种,但其年存活率为66%,这意味着捕食者捕食成功率仅为34%。MGO通过捕食者成功率PSR来避免算法陷入局部最小值,数学描述如下:

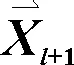
(11)

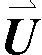
2.2.5 长短期记忆神经网络 LSTM在隐藏层单元中设计了遗忘门、输入门和输出门,利用输出门来控制单元状态ct的当前输出值ht,LSTM结构如图2所示。

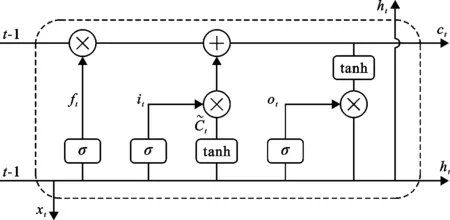
图2 LSTM结构示意图

设输入序列为(x1,x2,…,xT),隐含层状态为(h1,h2,…,hT),则在t时刻有[18-22]:

it=σ(Whiht-1+Wxixt+bi)

(12)

ft=σ(Whfht-1+Whfxt+bf)

(13)

ct=ft·ct-1+it·g(Whcht-1+Wxcxt+bc)

(14)

ot=σ(Whoht-1+Woxxt+Wcoct+bo)

(15)

ht=o·g(ct)

(16)

为使LSTM满足预测目的,需加上一个线性回归层,即:

yt=Wyoht+by

(17)

上式中各参数意义见文献[18]、[19]。

2.2.6 门控循环单元 GRU结构与LSTM类似,是将LSTM的更新门和遗忘门整合为新的更新门,相比于LSTM,其结构更加简单、训练参数更少,因此收敛速度也就更快[22-25],GRU结构如图3所示。

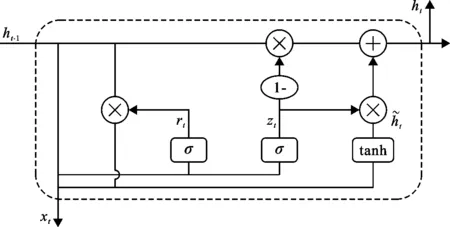
图3 GRU结构示意图

GRU的迭代公式如下:

zt=σ(Wz·[ht-1,xt])

(18)

rt=σ(Wr·[ht-1,xt])

(19)

(20)

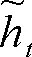
(21)

式中:z为更新门;r为重置门;W为权重矩阵;σ为sigmoid函数;h为输出值; *为哈达玛积(Hadamard product); 下标t表示t时刻。

2.3 预测步骤

WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU、WPT-CSA-LSTM、WPT-CO-LSTM、WPT-MGO-LSTM模型的预测步骤归纳如下:

步骤1:利用WPT将pH值及CODMn、DO、NH3—N浓度时序数据进行2层分解,分别得到1个趋势项分量[2,4]和3个周期项分量[2,1]～[2,3],其中趋势项分量可有效反映原始水质数据的趋势性,周期项分量可反映原始水质数据的微小震荡变化,如图4所示。

图4 pH值及CODMn、DO、NH3—N浓度时间系列数据的WPT分解

本文选取pH值及CODMn、DO、NH3—N浓度时序数据的70%作为训练样本,剩余30%作为预测样本。

步骤2:基于SPSS软件,利用偏自相关函数(partial autocorrelation function, PACF)确定各分解分量的输入步长k。经计算,pH值及CODMn、DO、NH3—N浓度趋势项分量[2,4]的k值均为1;周期项分量[2,1]～[2,3]的k值均为2,即利用前k周的水质数据预测当前水质。各模型的输入、输出可表述为:

(22)

(23)

式中:l为样本数量;k为输入步长。

步骤3:GRU/LSTM预测性能的优劣取决于其超参数的选择。本文利用2层GRU/LSTM网络进行预测,并利用各分量训练样本构建变色龙优化算法(CSA)、猎豹优化(CO)算法、山瞪羚优化(MGO)算法调优GRU/LSTM超参数的适应度函数f:

(24)

式中:m1、m2分别为第1、第2隐藏层神经元数;dr1、dr2分别为dropout_1、dropout_2参数;c为学习率;L1为Learn Rate Drop Period参数;L2为Learn Rate Drop Factor参数;下标min、max分别为各调优参数搜索空间上、下限值;其他参数意义同上。

步骤4:设置变色龙优化算法(CSA)、猎豹优化(CO)算法、山瞪羚优化(MGO)算法种群规模为30,最大迭代次数为100,其他采用算法默认值初始化变色龙、猎豹、山瞪羚空间位置。

设置GRU/LSTM超参数[m1,m2,dr1,dr2,c,L1,L2]搜索空间下限为[8,8,0.001,0.001,0.001,0.0001,0.1],上限为[128,128,0.5,0.5,0.5,1,1],激活函数选用tanh函数;SVM惩罚因子、核函数参数、损失系数搜索空间下限设置为[0.01,0.01,0.001],上限设置为[100,100,0.1],交叉验证折数设置为3,原始数据采用[-1,1]进行归一化处理。本文WPT-LSTM、WPT-GRU模型中的超参数采用试错法确定。

步骤5:基于公式(24)计算变色龙优化算法(CSA)、猎豹优化(CO)算法、山瞪羚优化(MGO)算法计算个体的适应度值,找到并保存最佳个体位置。令t=1。

步骤6:分别利用上述变色龙优化算法(CSA)、猎豹优化(CO)算法、山瞪羚优化(MGO)算法位置更新算子更新个体新位置。

步骤7:利用个体位置更新后的变色龙优化算法(CSA)、猎豹优化(CO)算法、山瞪羚优化(MGO)算法计算个体适应度值,再比较并保存当前最佳个体位置。

步骤8:令t=t+1,若t=T,则结束算法;否则返回步骤6。

步骤9:输出最佳个体位置,该位置即为最佳GRU/LSTM超参数向量。利用该向量建立WPT-CSA-GRU等6种模型对各分量进行预测和重构。

步骤10:利用平均绝对百分比误差MAPE、平均绝对误差MAE、均方根误差RMSE和决定系数DC对模型进行评价。其中,MAPE、MAE用于反映模型预测误差大小,RMSE用于衡量观测值与真值之间的偏差,MAPE、MAE、RMSE越小则说明模型性能越优、预测精度越高;DC反映变量之间相关关系的密切程度,其值越大则说明模型性能越好。

3 算法验证与结果分析

构建WPT-CSA-GRU等11种模型对实例断面(云南省昆明市观音山断面)pH值等4个水质指标进行训练及预测,预测结果评价及对比见表1,预测相对误差见图5。

注:预测模型序列1～11分别为WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU、WPT-CSA-LSTM、WPT-CO-LSTM、WPT-MGO-LSTM、WPT-GRU、WPT-LSTM、WPT-CSA-SVM、WPT-CO-SVM、WPT-MGO-SVM模型图5 各预测模型对实例断面4个水质指标预测结果的相对误差

依据表1及图5可以得出以下结论:

(1)WPT-CSA-GRU等6种模型对实例pH值预测的MAPE为0.230%～0.459%、MAE为0.019～0.037 mg/L、RMSE为0.023～0.046 mg/L,决定系数DC>0.993;对CODMn浓度预测的MAPE为0.991%～1.823%、MAE为0.096～0.182 mg/L、RMSE为0.129～0.228 mg/L,决定系数DC>0.991;对DO浓度预测的MAPE为1.200%～2.685%、MAE为0.073～0.154 mg/L、RMSE为0.094～0.201 mg/L,决定系数DC>0.984;对NH3—N浓度预测的MAPE为5.391%～11.383%、MAE为0.014～0.030 mg/L、RMSE为0.019～0.042 mg/L,决定系数DC>0.992,预测精度优于WPT-GRU、WPT-LSTM,远优于WPT-CSA-SVM、WPT-CO-SVM、WPT-MGO-SVM模型。以MAPE评价指标为例,WPT-CSA-GRU等6种模型对pH值及CODMn、DO、NH3—N浓度的预测精度较WPT-GRU、WPT-LSTM模型分别提高了45.1%、32.7%、15.9%、41.3%以上,较WPT-CSA-SVM、WPT-CO-SVM、WPT-MGO-SVM模型分别提高了68.2%、70.0%、67.7%、69.7%以上。可见,本文提出的WPT-CSA-GRU等6种模型具有较好的预测效果,应用于水质预测是可行的。其中,WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU模型的预测效果优于WPT-CSA-LSTM、WPT-CO-LSTM、WPT-MGO-LSTM模型,具有更高的预测精度和更好的泛化能力。

(2)WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU模型对pH值及CODMn、DO、NH3—N浓度预测的MAPE较WPT-GRU模型分别提高了62.9%、59.6%、40.8%、63.7%以上;WPT-CSA-LSTM、WPT-CSA-LSTM、WPT-CSA-LSTM模型预测的MAPE较WPT-LSTM模型分别提高了34.4%、36.7%、20.7%、43.6%以上,表明CSA、CO、MGO能有效优化GRU/LSTM超参数,不但提高了GRU/LSTM预测性能,而且还克服了人工调节超参数带来的高不确定性和效果不佳的缺点,其中CSA优化效果最佳。

(3)从模型预测效果对比来看,WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU模型的预测效果最佳,WPT-CSA-LSTM、WPT-CO-LSTM、WPT-MGO-LSTM模型预测效果次之,WPT-GRU、WPT-LSTM模型预测效果一般,WPT-CSA-SVM、WPT-CO-SVM、WPT-MGO-SVM模型预测效果最差;从4个水质指标的时序数据变化及预测效果对比来看,pH值时序数据起伏变化不大,预测效果最好;CODMn、DO时序数据起伏变化较大,预测效果较好;NH3—N时序数据起伏变化最大,预测效果相对较差。

4 讨 论

深度学习是由多个非线性映射隐含层组成的一种神经网络,能较好地挖掘数据之间的非线性。近年来,随着深度学习的快速发展,以LSTM、GRU为代表的深度学习已经成为当前研究的热点,并被广泛应用于水质预测[37-39]领域。LSTM是RNN的变种,克服了RNN面临的梯度消失和梯度爆炸问题,能够解决其他深度学习算法无法处理的时间长期依赖问题;GRU是LSTM的变种,是为解决长期记忆和反向传播中的梯度等问题而提出来的,与LSTM相比,GRU拥有更低的复杂度以及更好的预测性能。在实际应用中,LSTM、GRU预测精度和收敛性在很大程度上依赖于超参数(如层数、学习率、隐含层节点数等),而超参数的设置普遍采用手工试错的方法,难以满足GRU/LSTM预测需求。CSA、CO、MGO具有良好的全局搜索能力,应用CSA、CO、MGO调优GRU/LSTM超参数得到全局最优解,不但克服了LSTM、GRU易陷入局部最优从而影响预测精度的缺点,而且还使模型获得了较好的智能化水平。此外,水质时间序列具有较强的非线性和多尺度等特征,采用WPT进行分解处理,将水质时间序列分解为多个更具规律的模态分量,不但可降低模型预测器的预测难度,而且还大大减少了模型的预测误差。

GRU与LSTM相比,其在结构上更具优势,从WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU模型与WPT-CSA-LSTM、WPT-CO-LSTM、WPT-MGO-LSTM模型的pH值及CODMn、DO、NH3—N浓度预测结果对比来看,WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU模型利用重置门控制当前信息和记忆信息的数据量,并生将成新的记忆信息继续向前传递,具有更好的适应性与预测能力。

当然,本文提出的WPT-CSA-GRU等6种预测模型存在训练时间长、系统资源消耗大等缺点和不足。同时本文仅利用了云南省昆明市观音山断面pH值及DO、CODMn、NH3—N浓度的历史数据作为输入,未考虑滇池补水、水温以及降水等因素的影响,因此,该模型及预测精度仍有进一步提升的空间。

5 结 论

为提高水质时间序列的预测精度,本文提出了WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU、WPT-CSA-LSTM、WPT-CO-LSTM、WPT-MGO-LSTM预测模型,并构建了若干个对比模型,结合云南省昆明市观音山断面2004—2015年逐周pH值及CODMn、DO、NH3—N浓度预测算例,得到如下结论:

(1)本文提出的WPT-CSA-GRU等6种模型预测误差小于其他对比模型,具有较高的预测精度和较好的泛化能力,将其用于水质时间序列预测是可行的。其中WPT-CSA-GRU、WPT-CO-GRU、WPT-MGO-GRU模型对pH值及CODMn、DO、NH3—N浓度预测的MAPE分别在0.230%～0.310%、0.991%～1.093%、1.200%～1.891%、5.391%～7.030%之间,DC均在0.99以上,具有更好的预测效果。

(2)针对随机性、波动性较强的水质时间序列,利用WPT对其进行平稳化处理,可得到更具规律的趋势项分量和周期项分量,大大减少了混合模型的预测误差。

(3)针对GRU/LSTM因超参数选择不当而导致预测性能低下的问题,利用CSA、CO、MGO调优GRU/LSTM超参数,不但提高了GRU/LSTM的预测性能,而且克服了人工调节超参数带来的高不确定性和效果不佳的缺点。

(4)本文提出的模型及方法可为相关时间序列数据处理、GRU/LSTM超参数调优以及时间序列预测研究提供参考。