基于虚拟轴耦合的虚拟同步发电机混合储能惯量-阻尼协调控制策略
2023-09-11刘华志张祥宇李永刚
刘华志,覃 露,张祥宇,李永刚
(1.国网天津市电力公司电力科学研究院,天津 300220;2.国网天津市电力公司城西供电分公司,天津 300110;3.华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
0 引言
含高比例可再生能源发电的电力系统的暂态稳定性因功率支撑不足而受到了大量的关注。在可再生能源发电渗透率较高的系统中,功率振荡事件频繁发生,如新疆哈密、上海南汇地区,严重影响了电力系统的稳定运行[1]。为了实现可再生能源模拟同步发电机(synchronous generator,SG)的运行特性,虚拟同步发电机(virtual synchronous generator,VSG)技术得到了广泛的研究[2-3]。然而,与SG不同,VSG 的动态支撑能力主要取决于风电机组、光伏阵列、混合储能装置(hybrid energy storage device,HESD)中存储的可用能量[4-5]。同时,VSG 的虚拟惯量、阻尼是可控的,随着VSG 的广泛应用,VSG 和SG间的相互作用会给电力系统带来新的稳定问题。
现有研究已经验证了VSG 对频率支撑和振荡抑制的有效性,但虚拟惯量和阻尼设计仅针对单一的稳定性问题。文献[6]在分析系统稳定性时,保持虚拟惯量恒定,仅考虑了阻尼参数的影响。文献[7]利用VSG 为系统频率调节提供惯量支撑,但未详细讨论系统的阻尼效应。在VSG 中,阻尼和惯量的控制功能都依赖于有功功率调节。因此,在实际应用中,由于2 个控制之间不可避免地存在相互作用,无法达到预期的控制效果,虚拟惯量对系统阻尼有显著的影响[8]。文献[9]进一步表明,系统频率响应及波动的不同区间对惯量、阻尼的需求也不同。虚拟惯量设置不当会降低系统阻尼。由于系统中动态支撑电源的虚拟惯量和阻尼之间的矛盾难以化解,VSG的广泛使用将面临严重的运行风险。针对这一问题,文献[10-11]基于功角的摆动周期对风电机组进行变惯量调节,以提高互联电力系统的功角稳定性。文献[12]分析了VSG 阻尼参数对频率稳定性的影响,提出了一种惯量和阻尼交错自适应算法以保证系统的阻尼比。在此基础上,文献[13]同时考虑VSG 的功率和频率特性,利用自适应偏差调节器和自适应优先级设定器的双适应性惯量控制,进一步提升了控制器的性能。文献[14]通过分析不同转动惯量和阻尼系数下的有功环根轨迹,建立两者之间的自适应函数,以同时保证功率和频率的动态调节性能。文献[15-16]根据扰动后VSG 功率、功角、频率振荡过程的划分区间,实时协同调整惯量和阻尼,保证系统惯量的同时,提高了暂态恢复速度。为了满足系统在各种扰动下的稳定运行,自适应惯量和阻尼需要在大范围内频繁的切换,这对系统的储能容量和稳定性提出了更高的要求[17]。进一步地,文献[18]通过建立频率稳定优化模型,以发生扰动后系统的不平衡能量最小为目标,利用遗传算法实现虚拟惯量和阻尼的协调优化。文献[19]结合系统主导振荡模式在线辨识,利用粒子群优化算法协调优化VSG 控制器参数,缓解VSG 虚拟惯量与阻尼之间的矛盾。然而,由于VSG 的功率振荡抑制机理仍不清楚,对潮流方向的检测和复杂的逻辑算法都提出了更高的要求,这增加了实际应用的难度。
根据电力系统的暂态稳定机理,发电机的有效暂态能量传递对提高系统稳定性至关重要。理论上,电力电子变换器通过VSG 控制为HESD 承担SG暂态能量提供了巨大的潜力。然而,当前的VSG 失去了与SG 的联轴耦合关系。利用VSG 与SG 之间的轴系耦合获得两自由度对于提高HESD 电网的支撑能力具有重要的作用。在两自由度系统中,只有通过分析发电机之间的暂态能量传递规律,才能明确VSG 参与系统振荡抑制的机理,这将是优化VSG 支撑功能的重要理论依据。
为了提升混合储能VSG 的友好并网性能,本文首先根据蓄电池、超级电容器和SG 之间的能量转换关系,对HESD 惯量支撑能力进行估算,建立HESD静态能量与SG 动能之间的转换关系。在此基础上,为了从SG 中传递更多的暂态能量,在HESD 中引入新的虚拟轴,并分析HESD 与虚拟轴耦合对系统暂态稳定性的影响。利用哈密顿能量函数,推导HESD 暂态能量高效传递的必要条件,进而提出一种HESD 虚拟轴控制策略,实现虚拟惯量和功率振荡功能的整合。基于高渗透率光伏和混合储能系统进行验证,结果表明所提控制策略能显著提升系统的频率、功角暂态稳定性。
1 混合储能VSG的虚拟惯量
为了在延长储能装置使用寿命的同时实现其容量的高效利用,本文结合蓄电池内部容量大、响应时间长以及超级电容器损耗低、响应时间短、使用寿命长等优点,选择能量型和功率型相结合的混合储能进行虚拟同步控制。
1.1 蓄电池的虚拟惯量
根据固有惯量的定义,SG 的惯量响应是通过释放或吸收转子旋转质量中储存的动能而得到的。从理论上而言,储存在HESD 中的静态能量也可成为VSG 机组虚拟惯量能量的来源。但是,若要实现VSG 虚拟惯量的调节,则需要建立HESD 静态能量与SG动能之间新的转换关系。
在频率变化的初始阶段,SG 利用储存的动能为动态频率提供惯量支撑。因此,SG的动能Ek与发电机转子的固有惯量密切相关,可表示为:

式中:uB为蓄电池的输出电压;γSOC-0为蓄电池SOC的初始值。
结合式(2)和式(3),WB可表示为:

1.2 超级电容器的虚拟惯量
在混合储能中,存储在超级电容器中的静态能量也可以用于提供VSG 的惯量响应。同理,超级电容器的SOCρSOC可表示为:
式中:QC、uC分别为超级电容器的容量、输出电压;C为超级电容器的电容值。
超级电容器中存储的静态能量WC可表示为:

参考SG 惯量时间常数的概念,将HESD 的虚拟惯量时间常数HHV定义为:
式中:SH为HESD的额定容量。
由式(12)和式(13)可以看出,虚拟惯量通过释放或吸收储存在蓄电池、超级电容器中的静态能量,将HESD 与系统频率耦合。通过实时检测SOC 的变化,可以估算HESD 的虚拟惯量储备。此外,由式(6)和式(11)可知,HESD 的虚拟惯量主要由控制参数kB、kC决定。
2 SG和HESD的轴系耦合模型
虚拟惯量和阻尼控制回路组成的电流源型VSG控制结构如图1 所示。在虚拟角速度ωv的控制下,HESD 的功率响应与SG 类似,可用于系统惯量和阻尼支撑。其中,VSG 的阻尼控制也可以遵循SG 的设计。图1中:SG1经母线B4与HESD并联;G0为参考发电机;x1—x3分别母线B1—B3与母线B4之间的线路电抗;Pev、Pset分别为HESD 的输出功率、给定功率;Pe、δs分别为SG1的输出功率、功角;δv、DHV分别为VSG 的虚拟功角、阻尼系数;ω0为同步角速度;V1、V2、V3分别为SG1、VSG、G0的节点电压;id_ref为电流内环的电流参考值;vd为基准电压;u为电流内环输出的参考电压;Pref、ΔP分别为VSG 控制的有功功率参考值、惯量阻尼环节的功率变化量。为了便于分析HESD 中有功控制环节暂态能量的转移特性,本文选择电流源型VSG,并将其部署于DC/DC 换流器中,以减少HESD对电网运行的影响。
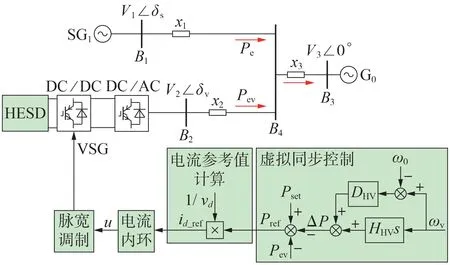
图1 含VSG的电力系统等效电路图Fig.1 Equivalent circuit diagram of power system with VSG
在分析电力系统的稳定性时,VSG 可以简化为SG。HESD的动力学方程可表示为:
式中:p为微分算子。
在同步运行过程中,由于VSG 与SG1并联接入电网,虽然VSG 的初始功角δv0与SG1的初始功角δs0不同,但功角的变化量近似相等,即Δδv≈Δδs。此时,两机组可等效为单机系统,运动方程可表示为:
式中:H=HS+HHV为VSG 和SG1的等效惯量时间常数,HS为SG1的固有惯量时间常数;DS为SG1的阻尼系数;ΔPe、ΔPev分别为SG1、VSG 输出有功功率的变化量;x13为G1和母线B3之间的线路电抗;x23为混合储能VSG 和母线B3之间的线路电抗;KS、KV为转矩系数。
在单自由度系统中,由于KS主要由系统的电路参数决定,通常忽略KS、KV对系统动态稳定性的影响。虚拟惯量和阻尼是当前VSG 的2 个重要控制参数。然而,配备电力电子变换器的HESD 具有较强的功率调节潜力。从理论上而言,除虚拟惯量和阻尼外,KS也是可以由VSG 调节的。由式(16)可知,发电机轴系的旋转位移由转矩系数KS、KV决定。参照振动力学,可将KV定义为VSG 连接母线B3的轴刚度,将KS定义为SG1连接母线B3的轴刚度。相较于同步转矩系数的概念,轴刚度更适用于分析VSG 与SG1间轴系功角的振荡特性。如果将柔性轴施加到VSG 上,则可以通过VSG 调节发电机轴的相对转动位移,从而建立更加灵活的两自由度系统。
由式(14)可知,在单自由度系统中,如果只考虑虚拟惯量控制,则HESD 中VSG 控制的有功功率变化量可表示为ΔP=-2HHVpωs。虚拟惯量随系统频率f变化的动态功率响应如附录A图A1所示。由图可知,ΔP仅在频率下降的初始阶段提供有效支撑,在随后的频率恢复期间,虚拟惯量产生负功率响应(ΔP<0),这主要是因为当频率开始恢复时,df/dt>0。由此可见,虚拟惯量会延长恢复过程,这不利于电力系统的动态稳定性。
进一步地,由式(16)可计算得到单自由度系统特征值的实部λS为:
由式(17)可知,随着HHV的加入,系统惯量增大,λS开始向虚轴移动,系统稳定性降低。
3 含虚拟轴控制的HESD暂态能量传递
3.1 虚拟轴的发电机组建模和小信号分析
在当前VSG 控制下,VSG 的功角变化始终与SG1保持同步。若VSG 和SG1之间的轴是刚性的,则振荡功率会从系统传递到相关的发电机组,VSG 和SG1之间不存在暂态能量传递。系统的功率流路径如图2 所示。图中:ΔPsv为虚拟轴的耦合功率;Pev_ref为虚拟轴控制输出的参考功率;ΔKSV为附加的虚拟轴刚度。
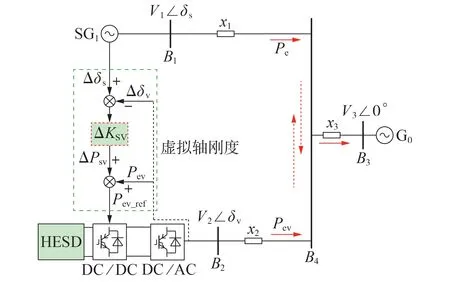
图2 含虚拟轴的电力系统的功率路径Fig.2 Power flow path of power system with virtual shaft
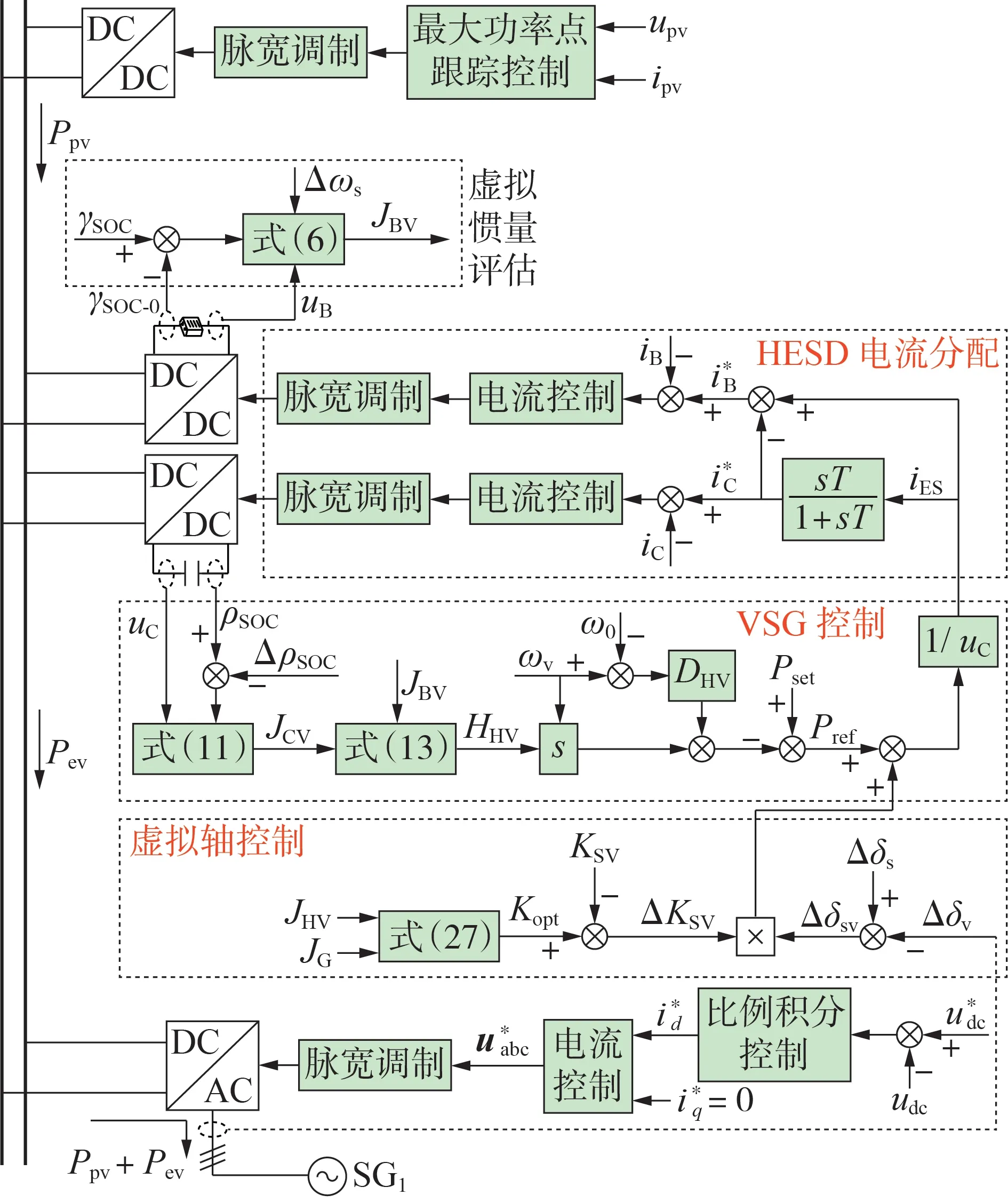
图3 暂态能量传递控制器结构示意图Fig.3 Structure diagram of transient energy transfer controller
为了研究混合储能的功率支撑潜力,需要在VSG 中引入新型柔性轴,从而使VSG 的功角与SG1的功角独立调节,即使Δδv≠Δδs。此时,机组间的功率交换如图2所示。SG1与HESD的VSG之间将存在能量相互作用。若SG1与VSG 具有相同的功角变化(Δδv=Δδs),则VSG 可视为采用刚性轴与SG 连接,2台机组间不存在动态功率转移。如图2所示,当且仅当VSG 与SG1通过柔性轴连接时,才能得到发电机组间功角的相对变化量Δδv-Δδs。
与传统VSG 控制不同,若HESD 的虚拟轴与SG1耦合,则SG1、VSG 的有功功率随着功角的变化(Δδs≠Δδv)而变化,可表示为:

由式(19)可知,若定义系统状态向量为Δx=[Δδs,Δωs,Δδv,Δωv]T(Δωv为ωv的变化量),则并网系统的状态方程表达式为Δẋ=AΔx,其中A为两自由度VSG 虚拟轴并网系统的状态矩阵,如附录A 式(A1)所示。
为了验证参数对虚拟同步控制的影响,分别调节HHV(变化范围为0~8 s)和DHV(变化范围为0~50)变化,系统特征值轨迹如附录A 图A2所示。由图可知,在虚拟同步控制下,随着HHV增大,特征值实部增大、虚部减小,逐渐向零点靠拢,振荡模态的阻尼比逐渐减小,系统响应速度减慢,降低了系统的稳定性。当DHV由0 增大至17 时,系统特征值实部、虚部均减小,逐渐向实轴靠近,系统阻尼比逐渐增大;然而,随着DHV进一步由17增加至35,系统由欠阻尼状态进入过阻尼状态。由上述分析可知,仅通过调节惯量和阻尼参数,仍难以协调两者间的矛盾。
通过在两自由度系统中引入新的虚拟轴参数KSV,可以增强VSG 与SG 之间的耦合。为了进一步分析KSV对VSG 并网系统的稳定性,调节KSV由0 变化至5,绘制系统特征值轨迹,如附录A 图A3 所示。由图可知,引入虚拟轴后,VSG 与SG 之间存在相对功角差,因此2 组特征值的运动轨迹不再重合,其中对系统稳定性影响较大的是距离虚轴较近的1 组共轭特征值。当KSV由0 增大到1.5 时,主导特征值逐渐远离虚轴,VSG 与SG 的功率耦合性增强,VSG 通过积极调动储能装置向系统提供更多的功率支撑,逐步提高了系统稳定性。随着KSV进一步增大,系统特征值轨迹出现拐点,特征值逐渐靠近虚轴,阻尼比减小,系统稳定性降低。因此,除了通过调节虚拟惯量和阻尼外,引入虚拟轴的VSG 并网系统还可通过调节虚拟轴系数,调和虚拟惯量和阻尼之间的矛盾,进一步提升系统的稳定性。
3.2 虚拟轴的发电机之间的暂态能量传递
相较于式(16),式(19)中引入了新的轴刚度系数KSV,HESD 与SG1通过虚拟轴相互作用。同时,变刚度的柔性轴可随着功角的独立变化而设计。引入虚拟轴后,VSG 和SG 具有2 个自由度,暂态能量可从SG1传递至VSG。
在此过程中,采用复变平均法和多尺度法建立含VSG 的电力系统新的哈密顿能量函数,可实现量化VSG 与SG1之间的暂态能量传递。通过在式(19)中引入新的时间尺度τ,可将两自由度电力系统的动力学模型变换为:

式中:θ(τ)为τ时刻Δδs的复变相位;n为积分常数。
由式(22)可知,SG1和VSG之间的能量传递与相位θ的变化密切相关。在扰动初期,暂态能量集中在SG1,即θ=0,此时ΔEG=εn2/2。如果能量完全转移到θ,则相位应满足θ=π/2,此时ΔEG=0。
将式(A9)代入式(21),则暂态能量ES可表示为:
式中:η=α-β。
由式(23)可知,当θ=0 时,系统的初始能量EH=(ε-K)n2/(2ε)。由此,相位正切值可表示为:

由式(26)可得系统的相位轨迹曲线,如附录A图A4 所示。当θ=π/2 时,SG1的初始能量可以全部传递到VSG,此时ES=(ε-K2+K1)n2/(2ε)。由此可见,如果将柔性虚拟轴控制器应用于VSG,则可以实现更高效的暂态能量传递。因此,由式(26)可得,虚拟轴控制优化后的刚度Kopt可表示为:
理论上而言,若根据式(27)设置刚度Kopt,则可满足θ=π/2,ΔEG=0,此时SG1的暂态能量可以完全转移到VSG。由此可见,与虚拟轴耦合的HESD 能够承担更多的暂态能量以提高系统的稳定性。可控虚拟轴的相位轨迹(细线)和SG 暂态能量变化曲线(粗线)如附录A 图A4所示。由图可知,发电机组的相位变化范围受限于虚拟轴的大小,当满足最优虚拟轴设计Kopt=2.25时,相位可达到π/2,反映至SG暂态功率则为ΔEG=0。这表明通过虚拟轴,SG 的暂态功率完全传递至风电机组中,风电机组可以高效地转移暂态能量。同时,由图A4可知,在整个相位变化周期内,优化后的虚拟轴可以持续高效地提高暂态功率的传递效率,使SG 的暂态功率维持在较低的水平。
3.3 HESD虚拟轴控制器设计


储能控制系统中增加了以下3个控制模块。
1)VSG 控制模块。若VSG 提供虚拟惯量HHV参与系统调节,则首先分别根据式(6)和式(11)计算蓄电池的虚拟惯量JBV和超级电容器的虚拟惯量JCV,然后根据式(13)设置虚拟惯量HHV,从而模拟SG 响应功率变化。VSG的阻尼参数为实际频率和额定频率的差值比例系数,其大小按照SG 下垂系数原则进行整定。参考电流iCV将被发送至电流分配模块。若超级电容器在过充电或过放电状态下工作,则虚拟惯量由蓄电池补偿。
2)虚拟轴控制模块。在虚拟惯量和阻尼控制的基础上,将新型虚拟轴控制添加到VSG 中。检测电压相位的偏差信号Δδv,根据相位偏差信号Δδs-Δδv,获得VSG 和SG 之间的功率传递。根据式(27)计算虚拟轴刚度Kopt。为了优化虚拟轴刚度,将Kopt减去VSG 的初始轴刚度KSV,得到附加轴刚度ΔKSV,如式(28)所示。
引入虚拟轴后,VSG和SG1之间的耦合关系如式(19)所示。控制模块的输出信号为VSG 和SG1之间的功率传输参考。
3)HESD 电流分配模块。将虚拟轴传递功率除以电压uC,并与HESD虚拟同步控制电流iCV相结合,可以得到集成后新的电流参考值iES。通过滤波环节按照响应速度可将iES分解为蓄电池的电流参考值i*B和超级电容器的电流参考值i*C。因此,虚拟惯量、阻尼和虚拟轴首先由超级电容器提供,剩余功率由存储在蓄电池中的能量补偿,从而获得所需的动态功率响应。光伏阵列和HESD 提供的输出功率通过DC/AC 变换器流入交流电网,变换器采用电压和电流双闭环控制。
4 算例分析
为了验证本文所提控制策略的有效性,在包含2 台SG(SG1和SG2)、光伏阵列和HESD 的电力系统半实物平台上进行实验测试,仿真平台如附录A 图A5 所示。在测试系统中,SG1、SG2的额定功率分别为160、100 kV·A,光伏阵列的额定功率为100 kW。HESD 由容量为50 A·h 的电池和电容值为10 F 的超级电容器组成。光伏阵列和HESD 通过DC/AC 变换器连接到总线B6。负载L1、L2的功率分别为150、100 kW。太阳辐照度设置为1 000 W/m2。
4.1 不同控制策略下的负荷扰动分析
为了验证本文所提控制策略对负荷扰动的作用,设置如下3种方案进行对比分析:①方案1,无附加控制;②方案2,VSG 控制,HHV=3 s,DHV=0.5;③方案3,虚拟轴控制,HHV=3 s,DHV=0.5,ΔKSV=0.2。为了比较不同方案对系统稳定性的性能影响,表1 给出了3 种方案下系统的模态分析结果。同时,设置负载L1在18 s 时增加50 kW,3 种方案下系统振荡频率和SG1输出有功功率PG的动态响应分别如图4 和附录A图A6所示。

表1 3种方案下系统的模态分析结果Table 1 Modal analysis results of system under three shemes

图4 3种方案下系统的频率响应Fig.4 Frequency response of system under three shemes
由表1 可知:当HESD 无附加控制时,系统关键振荡模式的阻尼比仅为0.099 和0.072,系统稳定性较差;在VSG 控制下,系统2种模态的阻尼比分别增加为0.109 和0.082,但在这种情况下,VSG 的惯量和阻尼之间的矛盾尚未得到妥善解决;在所提虚拟轴控制下,系统2 种振荡模态的阻尼比分别增加为0.115和0.085,系统稳定性得到显著提高。
由图4 可知,在初始阶段,系统的频率性能主要取决于SG1的固有惯量。然而,对比3 种方案:由于方案1 的惯量最小,频率偏差最大为0.5 Hz;在方案2下,虚拟惯量由VSG控制下的HESD 通过检测频率变化提供,频率偏差减小到0.25 Hz 左右,在系统频率降至最小值之前,VSG会产生正功率支持,因此通过添加虚拟惯量能减小系统频率的变化率;在方案3 下,即采用本文所提控制策略,系统频率跌落速度与方案2 相近,由于HESD 始终保持正向功率支撑,其与SG1共同分担负荷需求,因此系统频率的恢复性能最佳。由图A6 可知,在方案3 下,SG1的有功功率从13.3 kW 降低到8.2 kW,SG1的功率恢复时间和最大功率变化都得到了改善。可见,虚拟轴控制提高了SG1和HESD 之间的能量传递效率,有助于提高系统稳定性。
3 种方案下HESD 的SOC 和有功功率响应分别如图5和图6所示。由图5可知,相较于方案2,方案3下的HESD具有更大的调节深度,ΔρSOC由9 % 增大为12.7 %,ΔγSOC由0.35 % 增大为0.61 %。由图6 可见,本文所提控制策略具有较长的功率支持时间。在3种方案下,方案3的系统频率恢复周期最短。图5 中SOC 曲线表明,虚拟惯量支撑主要由超级电容器提供,蓄电池中储存的能量只能在频率下降的初始阶段进行调节,这有利于延长其使用寿命。

图5 3种方案下HESD的SOCFig.5 SOC of HESD under three schemes

图6 3种方案下HESD的有功功率响应Fig.6 Active power response of HESD under three schemes
4.2 短路情况下系统的动态响应
为了验证本文所提控制策略在系统阻尼方面的性能,18 s 时在母线B9上设置时长为0.1 s 的三相短路故障,3 种方案下SG1的功角δs、SG1的输出有功功率PG、HESD 的输出有功功率Pev和SOC 测试结果分别如图7 —9所示。

图7 3种方案下SG1的功角响应Fig.7 Power angle response of SG1 under three schemes
由图7 和图8 可知,在无附加控制时,功角连续振荡。虽然测试系统中的SG 采用了电力系统稳定器,但系统阻尼仍然不足,在光伏发电渗透率较高的测试系统中仍然缺乏功率调节能力。显然,HESD抑制振荡的能力对提高系统稳定性具有重要的意义。然而,在方案2 下,虚拟惯量由HESD 提供,如第2 章所述,这样虽然可以提高频率稳定性,但增加虚拟惯量会导致额外的功角振荡。相较于方案1,方案2 下功角的最大振荡幅度从5.2°增大为7.25°,功角振荡更剧烈,SG1难以抑制δs和PG的振荡。这是因为具有恒定虚拟惯量的HESD 产生了负阻尼效应,HESD 中惯量和阻尼之间的设计矛盾难以协调。相较于方案1,方案3 中δs的最大振荡幅度减小为2.75°,δs和PG的振荡持续时间缩短为5.9 s。同时,SG1的最大有功功率振荡幅度也从21 kW 减小为14 kW。显然,本文所提控制策略能提高系统的暂态稳定性。测试结果表明,SG1和HESD 之间的暂态能量传递有利于阻尼系统振荡。
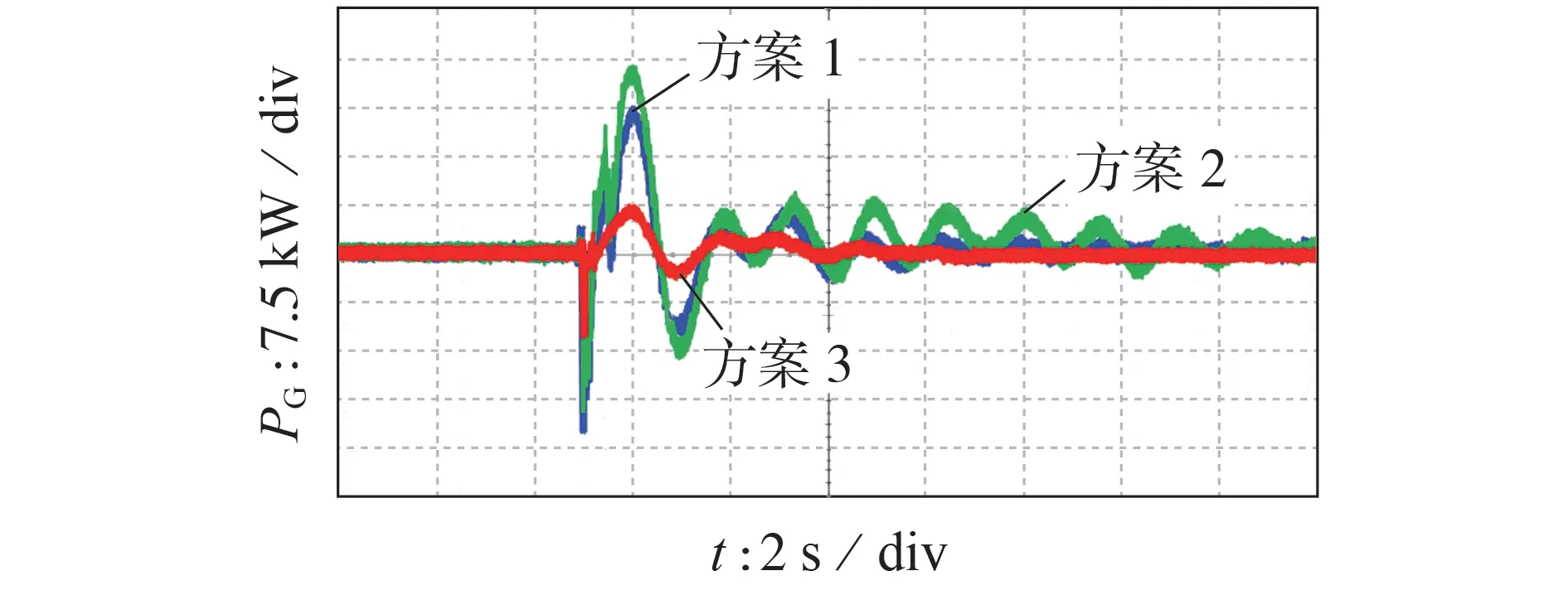
图8 3种方案下SG1的有功功率响应Fig.8 Active power response of SG1 under three schemes
由图9 可知,与方案1 和方案2 相比,方案3 下HESD、SG1与附加虚拟轴耦合,因此从SG1到HESD的瞬态能量传输效率最高,HESD 承受了更大的瞬态能量变化。相较于方案2,方案3 下ΔρSOC由3.7 %增加为6 %,这会对逆变器的过流能力提出更高的要求。方案2下HESD的电压、电流响应结果如附录A 图A7 所示。由图可知,虽然HESD 吸收了更多的瞬态能量,但其电流、电压仍在安全范围之内。可见,高效的暂态能量传输提高了HESD 抑制系统振荡的能力,本文所提虚拟轴控制策略可有效实现系统频率和功角的最佳动态性能。
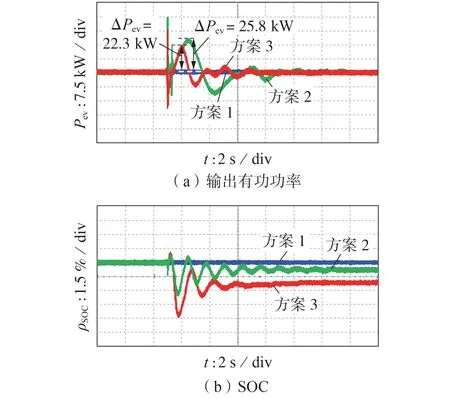
图9 3种方案下HESD的动态响应Fig.9 Dynamic response of HESD under three schemes
5 结论
本文利用虚拟轴将新的振动自由度应用于HESD的VSG 控制,实现了SG 暂态能量的高效传递,进一步挖掘了HESD 增强系统暂态稳定性的潜力,所得主要结论如下。
1)根据HESD 静态能量与SG 动能之间的转换关系,分别定义了电池和超级电容器的虚拟惯量。利用惯量储备,HESD 具有提供动态频率支撑的能力。然而,HESD 的虚拟惯量会对系统阻尼产生负面影响,甚至会导致系统失稳。
2)虽然VSG 可以提供虚拟惯量和阻尼,但在暂态过程中HESD 和SG 之间不存在功率传递。为此,在VSG 控制系统中引入虚拟轴,建立了HESD 与SG之间的动态功率耦合关系。HESD 的虚拟轴能够提供独立的功角变化以实现功率支撑,有利于提高机组间暂态能量的传递效率。
3)由哈密顿能量理论可知,在VSG 中引入虚拟轴后,虚拟惯量和阻尼参数可以通过所提HESD 的暂态能量传递条件进行协调设计。测试结果表明,HESD 中的虚拟轴能够提升系统频率和功率振荡支撑能力,显著降低了VSG的应用风险。
附录见本刊网络版(http://www.epae.cn)。
