基于等值频率响应模型的海上油田群电网风电穿透功率极限分析方法
2023-09-11苏开元邱银锋谢小荣李国香董文凯车久玮
苏开元,邱银锋,谢小荣,李国香,董文凯,车久玮
(1.清华大学 新型电力系统运行与控制全国重点实验室,北京 100084;2.中海油研究总院有限责任公司,北京 100028)
0 引言
在碳达峰、碳中和背景下,海上油田群电网将逐步增加海上风电接入容量以降低碳排放、节约发电成本[1-2]。然而,随着风电的穿透功率提升,其低惯性、波动性特点易导致电网频率大幅变动,以至于严重威胁电网的安全稳定运行[3]。因此,研究并确定海上油田群电网的风电穿透功率极限具有重要的现实意义。
风电穿透功率极限定义为电网在满足安全稳定运行条件下可接入的最大风电容量与电网最大负荷之比[4]。研究表明,当风电接入中小型电网时,应重点考虑频率对穿透功率极限的约束作用[5]。油田群电网作为海上微电网,发电容量远小于一般的陆上电网且常运行于孤岛状态[6],频率稳定更是其风电穿透功率极限的核心制约因素。
在计及频率稳定约束的风电穿透功率极限研究方面,文献[7]提出了一种考虑风电机组调频和稳态频率偏差约束、频率变化率约束的计算方法,并利用稳态频率偏差较小的特点对计算进行了简化;文献[8]针对风电波动引发的电网频率偏差问题,提出了计及储能系统的穿透功率极限计算方法;文献[9]通过全时域仿真方法分析了海上油田群电网暂态频率稳定与风电穿透功率间的关系。
上述文献表明,已有学者从电能质量角度对计及频率偏差约束的风电穿透功率极限计算做了较多研究,而涉及电网严重故障后暂态频率稳定约束的研究较少且复杂,使用全时域仿真分析油田群电网多工况、多故障情况需耗费大量时间。然而,对于频率易发生大幅波动的小型电网,高风电穿透功率下的暂态稳定问题是不可忽视的[6]。此种情况无法再以频率变化较小为前提进行近似,需要进一步研究其他分析方法。为此,文献[10]提出了黑启动过程中考虑系统暂态安全的动态风电穿透功率极限计算方法;文献[11-12]提出了基于等值频率响应模型的风电穿透功率极限求解方法,但该研究主要针对陆上电网,在考虑原动机-调速器时使用了再热式蒸汽轮机模型及参数。而海上油田群电网以微、小型燃气轮机为主体[13],有必要重新确定其等值模型及参数,以保证响应速度和求解结果的准确性。
针对上述问题,本文提出了一种适用于海上油田群电网的风电穿透功率极限分析方法。首先确定燃气轮机响应速度的影响参数及取值,建立海上油田群电网等值平均系统频率响应(average system frequency response,ASFR)模型、风电出力波动概率分布模型;然后提出频率偏差和暂态频率稳定双约束下的穿透功率极限分析方法;最后使用某实际海上油田群电网验证了所提方法的有效性。
1 海上油田群电网风电穿透功率极限计算模型
本章构建海上油田群电网ASFR 模型和风电出力波动概率分布模型,用以开展后续的风电穿透功率极限分析。
1.1 海上油田群电网ASFR模型
适用于小型电网的等值频率响应模型包括平均系统频率(average system frequency,ASF)模型、系统频率响应(system frequency response,SFR)模型和ASFR 模型[14-16]。ASF 模型保留了各原动机-调速器的独立响应,将全网发电机转子运动方程等值为单机模型。SFR 模型进一步将全系统等值为单机模型,但该模型未考虑各机组调速器参数不同的情况,在复杂电网中与实际结果偏差较大[17]。ASFR 模型在ASF 模型基础上,通过加权平均的方法确定单机模型等值参数,弥补了SFR模型在准确性上的不足。本文针对以微、小型燃气轮机为原动机-调速器的海上油田群电网,其系统相对较小,发输配用各部分紧密耦合[18],近似忽略频率时空分布特性和接入点影响,建立风电接入前后的ASFR单机等值模型。
1.1.1 风电接入前的ASFR模型
油田群电网中的微型燃气轮机通常为单轴结构(single-shaft gas turbine,SG)[19],其压气机、燃烧室和涡轮同属一轴系;容量为3~30 MW 的小型燃气轮机除单轴结构外,还包括以航改型燃气轮机为代表的分轴燃机结构(twin-shaft gas turbine,TG)[20],即负责输出有功功率的低压涡轮独属另一轴系。根据同步机转子运动方程,风电接入前功率-频率的频域关系满足式(1)。
式中:ΔPd为扰动功率;Δf为电网频率变化量;ΔPmSi、ΔPmTj分别为第i台单轴、第j台分轴燃气轮机响应电网频率变化的机械功率变化量;n、m分别为电网单轴燃机、分轴燃机数量;Hsys和Dsys分别为电网的等值惯性时间常数和等值阻尼系数;HSi、DSi、SSi和HTj、DTj、STj分别为第i台单轴和第j台分轴燃气轮机的惯性时间常数、阻尼系数、额定容量。
由于ΔPmSi、ΔPmTj均可表示为频率变化的函数,进一步扩展式(1),基于文献[8,19-21]所述的燃气轮机简化数学表示,构建海上油田群电网ASF 模型见图1。对于单轴燃气轮机,RS为调差系数,其与XS、YS、ZS共同描述燃料进料动态过程;TFS为燃料系统时间常数,TCDS为压气机排气时间常数,代表燃机能量转换的动态过程;λS为各机组额定容量与电网总装机容量之比。对于分轴燃气轮机,RT为调差系数;KPT、KLT为进料量控制参数;TFT、λT分别为燃料系统时间常数、各机组额定容量与电网总装机容量之比;由于高压、低压涡轮分属不同轴系,分轴燃机另有THPT代表高压涡轮时间常数。单、分轴燃气轮机响应速度影响参数及其典型值[8,19-21]见附录A表A1。
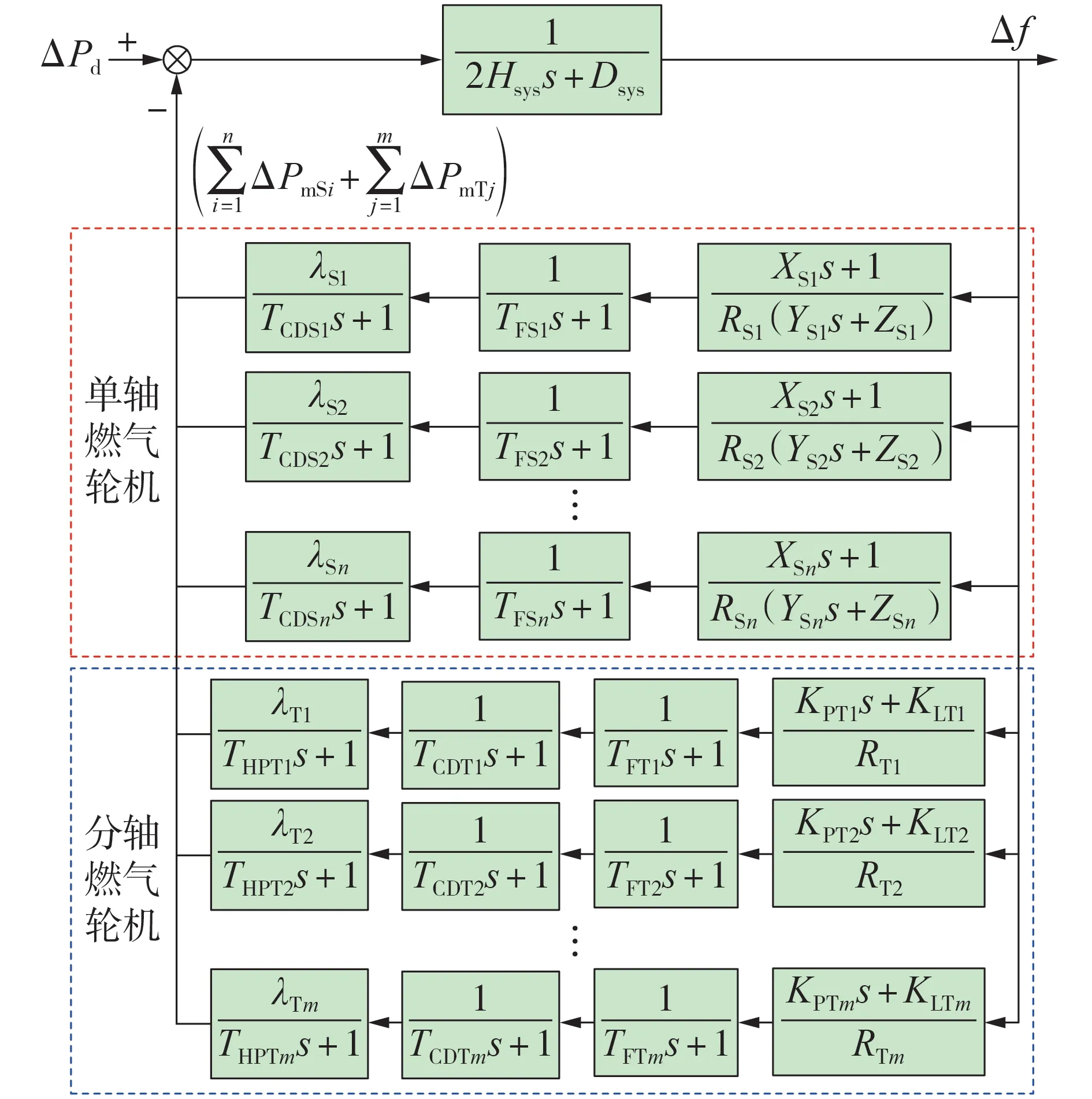
图1 海上油田群电网ASF模型Fig.1 ASF model of offshore oilfield power system
对于图1 中的各传递函数串联环节,忽略较小的时间常数对应YSs、TCDTs项、代入ZS=1,对其他参数进行等值,确定海上油田群电网ASFR 模型如附录B 图B1 所示。各等值参数计算方法如式(3)所示,以机组额定容量占比和调差系数为权重进行加权平均[16]。
式中:R为电网等值调差系数;X、K为燃料控制环节等值参数;T1、T2为能量转换环节等值时间常数。
1.1.2 风电接入后的ASFR模型
目前,海上油田群电网工程多采用跟网型海上直驱风电机组[22]。相比于构网型控制,跟网型控制下的频率支撑能力相对有限[23],加之附加频率控制的参数设计并非本文重点,此处作保守估计,暂不计及风电机组惯量响应和一次调频能力。该情况下,ASFR 模型中的等值惯性时间常数和等值调差系数将在风电机组接入后变化。定义λW为风电接入容量与全网运行机组容量之比,则有[24]:
式中:Hsysw和Rw分别为风电接入后电网的等值惯性时间常数和调差系数。
基于风电接入后的ASFR 模型,可求得任意扰动功率ΔPd对应的油田群电网频率响应表达式为:
以负荷功率骤增为例,在此阶跃扰动下,电网的频率响应曲线如图2 所示,通过求取最值即可确定最大频率变化Δfmax。

图2 阶跃扰动后电网的频率响应曲线Fig.2 Frequency response curve after step disturbance
1.2 风电出力波动概率分布模型
本文使用概率密度函数(probability density function,PDF)描述风电出力波动的概率分布特性。研究表明,tlocation-scale 模型[25]可以较简单且准确地反映风电出力波动ΔPw的概率特征。在该模型下,ΔPw的PDFfΔPw表示为:
式中:ν、σ、μ分别为形状、尺度和位置参数。
一般而言,各地区的风电出力波动数据不易直接获得,需要从实际风速与风电出力数据中分离得到。使用一阶差分变换方法[26],在确定了波动时间间隔ΔT后,风电出力波动可表示为:
式中:Pw(T)为T时刻风电场总出力;nw为风电机组接入台数;PN为单台风电机组额定容量。由该式可知,ΔPw取值范围为[-1,1]p.u.。
根据所得风电出力波动数据,将[-1,1]p.u.均分为若干波动区间,计算各区间概率密度,即可得到ΔPw的概率密度直方图。对该直方图使用tlocationscale 分布进行拟合,确定ν、σ、μ等参数,最终完成ΔPw的PDF计算,结果见图3。图中ΔPw为标幺值。
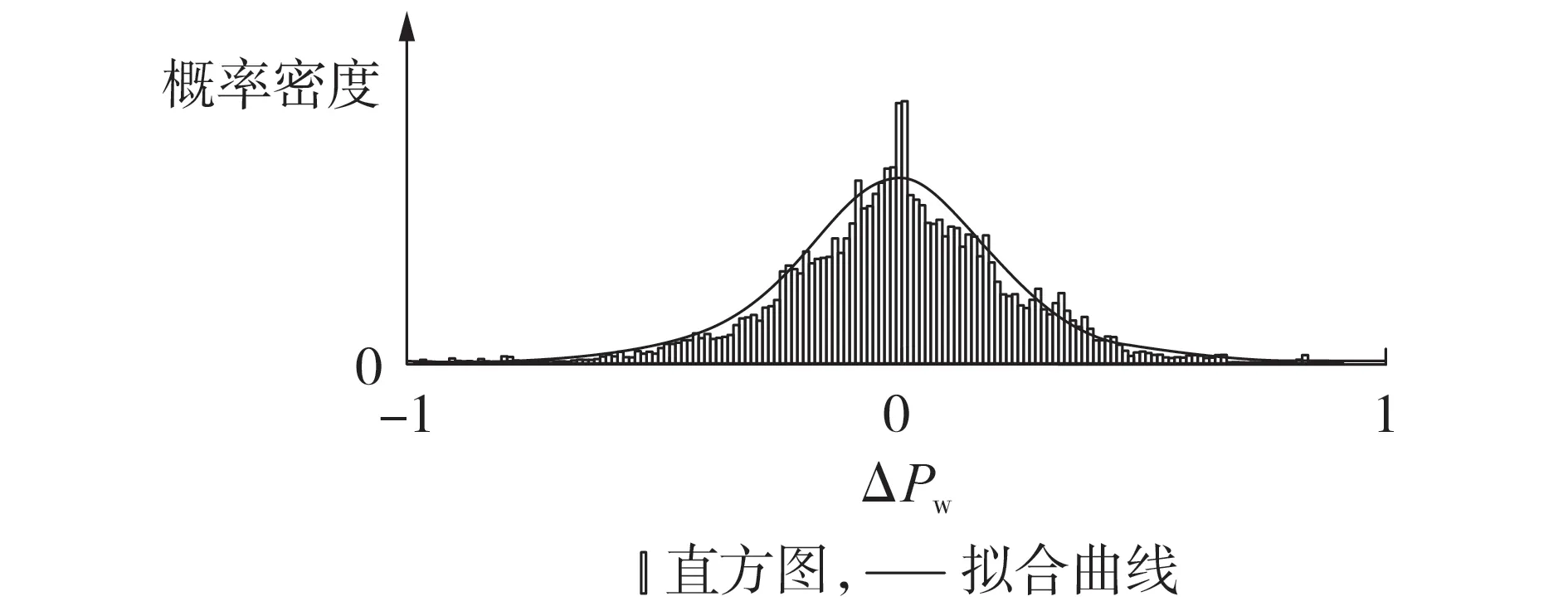
图3 风电出力波动PDF示意图Fig.3 Schematic diagram of PDF of wind turbine output fluctuation
2 海上油田群电网风电穿透功率极限分析方法
基于上述计算模型,下面综合考虑稳态频率偏差约束和暂态频率稳定约束,提出海上油田群电网风电穿透功率极限分析方法。
2.1 受频率偏差约束的极限计算
海上油田群电网容量较小[27],根据电能质量国家标准,其正常运行条件下的频率偏差限值设定为±0.5 Hz[28]。在此基础上,对于受频率偏差约束的海上油田群电网风电穿透功率极限计算,以电网可承受的最大风电波动对应累积概率是否满足要求为判据进行求解,具体步骤如下。
1)根据燃气轮发电机组、风电机组、负荷等元件参数,建立海上油田群电网ASFR 模型,确定风电机组接入台数初值。
2)根据风况及风电机组出力数据,建立风电出力波动概率分布模型,完成PDF计算,并根据风电机组接入台数变化不断修正Hsysw和Rw。
3)基于ASFR 模型和风电出力波动模型,改变电网扰动功率ΔPd,计算频率偏差约束下电网可承受的最大风电波动ΔPwmax。ΔPd可表示为实际扰动功率与系统中能够提供频率响应的总有功功率PB之比,在模拟风电出力波动时,将出力随时间变化的过程近似为斜坡函数,如式(8)所示。
4)根据式(9)判断电网可承受的最大风电波动对应累积概率Cdevia是否满足要求。
式中:Pr(·)表示概率;β为累积概率最小值,通常取为0.8[12]。若Cdevia≥0.8,则说明在80 % 及以上的波动情况下,电网满足频率偏差要求。
5)不断增加风电机组接入台数,重复上述过程,确定满足频率偏差约束下的风电穿透功率极限。
2.2 受暂态频率稳定约束的极限计算
除正常运行状态下的频率偏差约束外,故障后电网的暂态频率稳定同样制约着风电穿透功率极限。根据电力系统安全稳定计算规范,应限制暂态频率不低于各电源低频保护的最低值[29],海上油田群电网中燃气轮机低频限制为47 Hz,即电网暂态频率变化不得超过3 Hz。因此,对于受暂态频率稳定约束的海上油田群电网风电穿透功率极限计算,以最严重扰动下电网最大频率变化是否满足要求为判据进行求解,具体步骤如下。
1)与2.1 节同理,确定风电机组接入台数初值,根据接入台数变化修正ASFR模型参数。
2)确定电网最严重扰动及其对应功率ΔPd。对于暂态稳定问题,应根据元件产生或传输功率水平确定其扰动严重程度[30]。针对风电接入海上油田群电网的场景,海上风电场因送出系统故障整体切出可视为最严重扰动。此外,海上风电易受极端天气影响[31],风速突增情况下,其出力可能会因保护停转而直接下降为0。由于上述过程动作时间短,可使用阶跃函数描述其扰动,将ΔPd表示为:
3)根据ΔPd求取电网频率响应,根据式(11)判断电网最大频率变化Δfmax是否满足要求。
式中:ΔfS为频率变化允许值,按照稳定要求取值3 Hz。若电网满足暂态频率稳定要求,则继续增加风电机组接入台数,直至临界稳定状态,确定穿透功率极限。
4)为使计算结果更加准确,对所得结果进行N-1校核与限幅环节验证。对于N-1 校核,可选取最大容量燃气轮发电机组切出故障,验证所得风电机组接入台数下是否满足暂态频率稳定标准;对于限幅环节验证,在模型中加入燃料控制限幅环节(如附录B图B2所示),对极限计算结果予以验证,一般而言,单轴燃气轮机限幅环节取值为-0.1~1.5 p.u.[20],分轴燃气轮机限制下限为0.19 p.u.[22]。
2.3 风电穿透功率极限分析方法及其流程
综合2.1、2.2 节的计算方法,海上油田群电网风电穿透功率极限分析流程如图4 所示。在确定海上油田群电网基本参数、等值ASFR 模型和风电机组接入台数初值后,对频率偏差约束条件和暂态频率稳定约束条件下的穿透功率极限进行并行计算,取两者计算结果的最小值,从而确定电网可接入最大风电容量及极限计算结果。
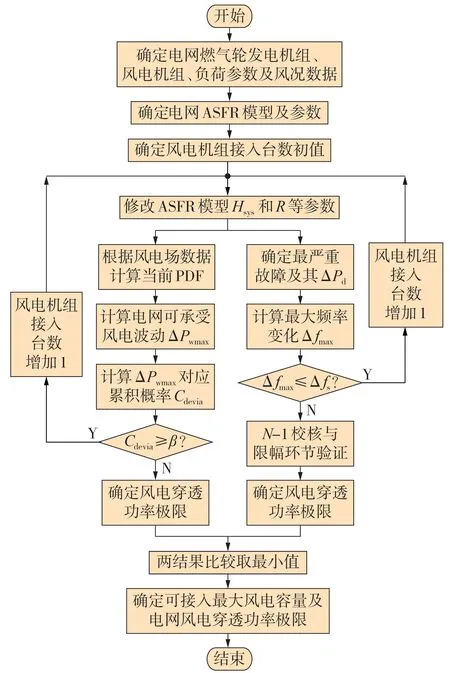
图4 风电穿透率极限分析流程图Fig.4 Flowchart of solving wind power penetration limit
3 仿真算例分析
以某实际海上油田群电网为例验证本文所提分析方法有效性,其整体拓扑结构如附录C 图C1 所示。该油田群电网包含4 个主要油田平台,总装机容量为185.224 MW,最大方式下负荷为103.83 MW。电网拟接入海上风电机组的单机容量为6 MW。基于该油田群电网实际情况,已知开机工况1如表1所示,另有工况2 作为研究过程中的校核对照工况。表中:24.09、28.77、10、25、19.5 MW 为各机组额定容量。
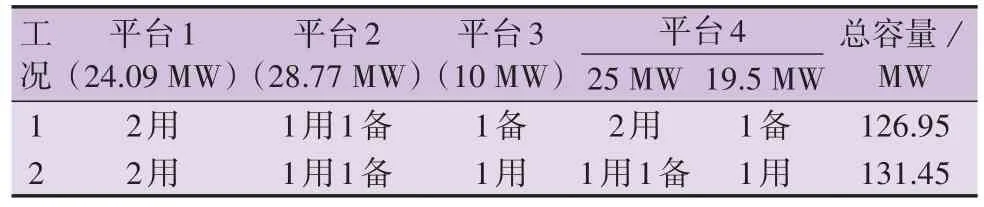
表1 油田群电网开机工况Table 1 Actual working status of oilfield power system
根据附录C 表C1、C2 所示的各发电机组及单、分轴燃气轮机参数,确定风电机组接入前该油田群电网ASFR 模型初始等值参数,如附录C 表C3所示。在穿透功率极限计算过程中,ASFR模型等值参数按照风电机组接入容量不断修正。
通过对比分析明确原动机-调速器响应速度影响,验证本文所提穿透功率极限计算方法的有效性,具体为:①在频率偏差约束下,比较全时域仿真方法、本文所提基于油田群电网ASFR 模型的分析方法、原基于文献[11-12,15]模型及参数的再热式蒸汽轮机ASFR 模型的分析方法(原ASFR 方法)三者的求解结果,验证本文所提方法准确性;②在暂态频率稳定约束下,比较三者求解结果,验证本文所提方法准确性;③比较仅考虑频率偏差约束与本文所提双约束下的求解结果,分析加入暂态频率稳定约束对结果的影响及特点。
3.1 受频率偏差约束的计算结果比较
该海上油田群电网实测风电出力曲线如附录C图C2所示,以此确定风电出力波动PDF 及电网可承受的最大风电波动对应累积概率Cdevia。
以工况1 为例,Cdevia随风电机组接入台数及风电出力波动ΔPw的变化关系见附录C图C3。可以看出,随着风电机组接入台数的增加,电网可承受的最大风电波动ΔPwmax在逐步下降,进而使得Cdevia逐步减小。当接入10 台风电机组时,ΔPwmax对应的Cdevia小于最小累积概率0.8,不再满足频率偏差要求。
使用全时域仿真方法、本文所提方法和原ASFR方法,计算得到频率偏差约束下的临界风电机组接入台数nw、电网可承受最大波动ΔPwmax及累积概率Cdevia如表2 所示。各工况下,本文所提出的分析方法与全时域方法所得风电机组最大接入容量一致,且同条件下ΔPwmax和Cdevia计算结果相对偏差均小于2.88 %,在频率偏差约束下具有相当的准确性。而由于原动机-调速器频率响应速度的显著差异,使用原ASFR 方法所得结果误差较大,在工况1下风电机组最大接入容量相对误差达80 %。
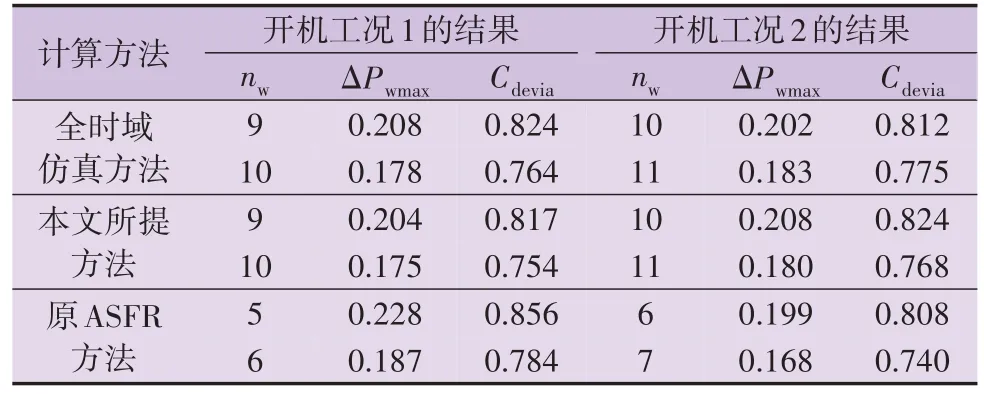
表2 频率偏差约束下的计算结果临界值Table 2 Critical value of calculated results under constraint of frequency deviation
3.2 受暂态频率稳定约束的计算结果比较
在海上风电场切出这一最严重故障下,使用上述3 种方法分别计算不同风电机组接入台数对应的最大频率变化Δfmax,将其转换为频率最低值fmin曲线如图5所示。

图5 最严重故障下电网频率最低值与风机台数关系Fig.5 Relationship between minimum frequency and number of wind turbines under most serious fault
由开机工况1、2下的结果可知,本文所提方法与全时域仿真所得风电机组最大接入容量相同。定义本文所提方法的结果Δfcamax相对全时域仿真方法的结果Δfsimax的误差rmax=|(Δfcamax-Δfsimax)/Δfsimax|×100 %。相同故障条件下,图5中工况1、2下的rmax<4 %,能够在较准确地反映电网暂态频率变化的同时将求解时间从分钟级减少至秒级。而与3.1节同理,由于燃气轮机与蒸汽轮机响应速度的差别,原ASFR 方法在工况1、2下的最大风机接入台数分别为5、6台,与全时域仿真方法所得的8、9台存在显著偏差。
3.3 不同约束下的计算结果比较
综合3.1、3.2 节计算结果,整理得频率偏差与暂态频率稳定约束下,该海上油田群电网风电穿透功率极限的计算结果如表3 所示。表中:①、②、③分别对应稳态频率偏差约束、暂态频率稳定约束的结果以及两者中的较小值。比较可知,考虑海上风电场切出的严重扰动,暂态频率稳定约束在计算结果中起主导作用。仅考虑风电出力波动后的频率偏差约束会使计算结果相对乐观,使用频率偏差与暂态频率稳定双约束则可以更好地满足电网安全稳定运行需求。

表3 频率偏差与暂态频率稳定约束下的计算结果Table 3 Calculated results under constraints of frequency deviation and transient frequency stability
4 结论
本文提出了一种基于等值频率响应模型的海上油田群电网风电穿透功率极限分析方法,主要结论如下。
1)所提出的风电穿透功率极限分析方法考虑了单、分轴燃气轮机动态响应过程和风电波动过程,能够在简化计算的同时保证准确性。
2)设定频率偏差与暂态频率稳定双约束,可使极限分析结果更好地满足电网安全稳定运行要求。考虑海上风电场切出的严重扰动,暂态频率稳定约束在极限计算中起主导作用,而单纯考虑风电波动下的频率偏差约束会导致偏乐观的结果。
3)原动机-调速器响应速度对海上油田群电网的风电穿透功率极限具有关键影响。使用燃气轮机与再热式蒸汽轮机等值模型所求解穿透功率极限具有显著差异,两者间误差最大可达80 %。现有工程中风电不具备虚拟惯量或快速调频控制,未来需进一步探讨风电、储能采用惯量和快速调频控制对系统稳定性的影响。
附录见本刊网络版(http://www.epae.cn)。
