考虑同步机制的双馈风电系统小扰动建模与稳定性分析

韩平平，汪宗强，南国君，谢毓广，李金中，张征凯

（1.合肥工业大学 新能源利用与节能安徽省重点实验室，安徽 合肥 230009；2.国网安徽省电力有限公司电力科学研究院，安徽 合肥 230061；3.国网安徽省电力有限公司，安徽 合肥 230061）

0 引言

近年来，风电等新能源装机容量逐年增加，其中双馈感应发电机（doubly-fed induction generator，DFIG）以成本低、运行可靠性高等优点在风力发电机中占据主流地位［1-2］。DFIG 依托电力电子装备并入电网，与同步机依靠转子运动来实现与电网自然同步的机制不同，电力电子装置同步机制体现在对并网变换器的控制，主要分为锁相环（phase locked loop，PLL）同步机制和虚拟同步发电机（virtual synchronous generator，VSG）控制型等自同步机制［3-4］。

PLL 同步机制结构简单，在强电网下的性能优秀，且在单机系统下方便对装备实现解耦控制［5］。利用阻抗建模法可以对系统稳定性进行分析，文献［6］与文献［7］分别建立类Heffron-Phillips 模型与DFIG 机组输入导纳模型，分析了PLL 对弱电网下DFIG 系统稳定性的影响机理。文献［8］通过序阻抗分析方法，搭建了含有PLL 的DFIG 系统序阻抗模型，分析了PLL 对系统输出的影响。利用特征值分析法也能够对系统进行小扰动建模并进行稳定性分析，其可以提供大量系统特征信息。文献［9］建立了含有PLL 的DFIG 机组模型，利用特征值分析了不同电网强度对系统振荡的影响规律，得出了PLL 是导致DFIG系统在弱电网下振荡的主导因素这一结论。文献［10］建立了DFIG 系统的全维状态空间模型，使用状态空间分析法对DFIG 并网的次同步振荡问题进行了研究，分析了PLL 同步机制及频率支撑对次同步振荡的影响。通过以上文献可得出，PLL 同步机制因被动跟踪电网且进行解耦控制，使电网呈现低阻尼、低惯量等特征，在弱电网下稳定性降低且易产生振荡［11］。

VSG 同步机制采用自同步方式，能够避免上述因PLL带来的影响。文献［12］针对VSG同步机制下的逆变器，采用序阻抗分析法对电网强度及并网逆变器台数改变时的稳定性进行了分析，但以上研究主要针对逆变器，不适用于DFIG系统的分析。文献［13］在考虑源端特性基础上，搭建了VSG 同步机制下直驱风机的小信号模型，分析了模型各参数变化时系统稳定的变化趋势，但直驱风机与DFIG系统仍存在一定差异。文献［14］提出VSG 同步机制能够对电网提供电压、频率支撑调节，并与传统电流源型控制进行比较，证明了VSG 同步机制在提高弱电网稳定性及提供惯量支撑方面具有优势。文献［15］对VSG同步机制与电网直接并网时出现的并网失败问题，提出了一种无PLL型的VSG预同步控制方法，提高了在弱电网下的并网可靠性。由上述分析可知，采取VSG 同步机制时，能够提升系统稳定性，且能够改善电网低阻尼、低惯量等现象［16-17］。

以上研究大多针对某种同步机制在弱电网下稳定性以及是否提供惯量支撑等方面进行分析，未对2 种同步机制下的DFIG 系统在同一条件下进行稳定性建模，也未针对二者的动态特性及小扰动特性进行机理对比及仿真验证。基于此，本文在考虑同步机制基础上，首先分别对PLL 和VSG 这2 种同步机制下的DFIG系统进行统一建模，得出二者的动态方程并求得系统的小扰动模型。其次利用特征值分析法计算出二者的特征根及相关特性参数，分析电网强度与弱电网下串补度对小扰动稳定性的影响，并对VSG 同步机制引入的虚拟惯量及阻尼系数改变时小扰动稳定性进行了分析。然后从有功动态特性以及小扰动稳定性2 种角度对不同同步机制下的DFIG 系统进行StarSim 硬件在环（StarSim-hardwarein-the-loop，StarSim-HIL）半实物仿真及解释分析。最终总结了2种同步机制对DFIG系统的适用性。

1 DFIG系统及同步机制方法

1.1 DFIG系统模型

DFIG 系统主要由风力机、感应发电机、转子侧变换器（rotor-side converter，RSC）和网侧变换器（grid-side converter，GSC）组成的背靠背双脉宽调制（pulse width modulation，PWM）变换器、网侧滤波器、接口线路等组成。DFIG 单机无穷大系统及相关物理参数可分别见附录A 图A1 和表A1。本文重点考虑不同类型的同步机制下风机小扰动稳定性问题，对于DFIG 轴系的动态过程可做简化处理，将其视作单质量块处理［18］，其动态方程如式（1）所示。

式中：H、Dz分别为等效单质量块的惯性时间常数、阻尼系数；θs为该单质量块的扭转角度；ωm、ωr、ωb分别为风轮角速度、发电机转子角速度、系统基准角速度；Tm、Te分别为风轮的机械转矩、发电机的电磁转矩；p为微分算子。

发电机的电磁转矩可用定、转子电流表示为：

式中：np为极对数，本文中取np=3；ωs为定子角速度；Lm为定转子之间的互感；isd、isq和ird、irq分别为定子和转子电流的d、q轴分量。

因风电场等新能源与负荷中心呈逆向分布，故需要进行长距离输电，DFIG 系统并网时常常串联补偿电容以减小输电线路阻抗。输电线路的串补度k用来表示输电线路中所串联电容的大小，其表达式如式（3）所示。

式中：XC为输电线路容抗；XL为输电线路感抗。

串补线路状态方程及代数方程如式（4）所示。

式中：RL、CL分别为输电线路电阻、电容值；id、iq分别为输电线路电流的d、q轴分量；ucd、ucq分别为输电线路串联电容电压的d、q轴分量；ubd、ubq分别为输电线路接入无穷大电网电压的d、q轴分量。

1.2 PLL型并网控制

PLL 是当前新能源装备并网最常采用的同步单元之一。本系统中利用定子电压定向控制方法，即将定子电压相量与旋转坐标系d轴重合。电压经过PLL 后，会保持与定子电压的相位一致。PLL 模型的微分方程为：

式中：θPLL为检测处电压超前d轴坐标系的角度；xPLL为PLL 追随定子电压q轴分量usq的积累误差；ωPLL为检测处的角速度，并将其作为系统旋转dq坐标系的参考电角速度；kp_PLL、ki_PLL分别为控制器比例、积分系数。

在PLL 同步机制下，RSC 采取定子电压定向控制方法，其主要目的是对发电机的转速进行控制或者对有功功率进行控制，即进行最大功率追踪，另外还能对电机输出功率进行控制。因此本文RSC采用功率、电流双闭环的控制策略［19］。GSC 控制器的主要目的是稳定GSC 与RSC 之间的直流母线电压，并能够控制交流侧的功率因数。该同步机制下RSC、GSC 控制策略及相关控制参数分别见附录B 图B1、B2及表B1。

1.3 VSG型并网控制

DFIG 系统中采用VSG 同步机制的逆变器可以等效成一种电压源，通过模拟同步机的同步过程，引入转子运动方程及电磁方程，首先利用控制环节来实现对幅值和功角的控制，得到定子的电压幅值及相角；然后利用电压环与电流环对功率输出进行控制，其中有功功率、无功功率分别由电压的相位角、幅值调节。在VSG 同步机制下可以通过调整参数获得虚拟惯量和阻尼特性。VSG同步机制框图如图1 所示。图中：Tj、D分别为虚拟惯量、阻尼系数；Ps_ref、Ps分别为定子有功功率的给定参考值和实际值；ωvsg、ω1分别为虚拟角速度和电网角速度；Qs_ref、Qs分别为定子无功功率的给定参考值和实际值；kpv、kiv分别为无功功率比例、积分系数；Us_ref、Us分别为定子电压幅值的给定参考值和实际值。

图1 VSG同步机制框图Fig.1 Block diagram of VSG synchronization mechanism

VSG同步机制中定子电压相角计算过程为［20］：

式中：θvsg为通过VSG 同步机制得到的定子电压相角；z1、z2为中间状态变量。定子电压幅值可表示为：

式中：z3为中间状态变量。针对图1 所示的控制策略，引进状态变量z4—z7，对RSC 需采用电压外环电流内环的控制方式。VSG 同步机制下DFIG 的RSC控制策略及控制参数可见附录B图B3及表B2。

2 DFIG系统小扰动模型分析

2.1 小扰动计算

为获得上述DFIG 系统的小扰动模型，需对该系统线性化，首先计算系统在某个平衡点处的初始值。若风速已知，可根据风力机相关公式及控制策略进行初始化，从而得到初始平衡点。

DFIG单机无穷大系统的小扰动方程为：

式中：Δx为小扰动方程状态变量；H为该系统的状态矩阵；A、B、C、D分别为各状态变量对应的系数矩阵。小扰动方程推导过程可见附录C。

通过式（9）可得系统的状态矩阵H，从而建立相应的特征方程，如式（10）所示。

式中：E为单位矩阵；λ为特征值。

2.2 VSG同步机制下的风机小扰动模型

因VSG 同步控制所得到的相角与电网相角之间存在偏差，在动态运行过程中定子电压所在坐标系和电网电压坐标系无法保持一致，在进行小扰动建模时，应考虑二者之间的偏差，考虑偏差相关过程见附录C 式（C1）—（C4）。考虑偏差并进行线性化后，系统的小扰动方程为：

式中：Δxvsgd、Δxvsgq、Δxd、Δxq分别为VSG 及电网两坐标系下小扰动方程状态变量的d、q轴分量；Xd0、Xq0分别为平衡点处状态变量初始值的d、q轴分量；Δδ为两坐标系之间的角度偏差小扰动量。在针对轴系模型进行线性化时，风轮角速度微增量Δωm和机械转矩微增量ΔTm对系统系数矩阵无影响，可忽略不计［17］。

考虑上述因素，VSG 同步控制下DFIG 系统小扰动方程状态向量可由14 个状态变量组成，该状态向量Δx=［Δωr，Δird，Δirq，Δisd，Δisq，Δz1，Δz2，Δz3，Δz4，Δz5，Δz6，Δz7，Δucd，Δucq］，Δ表示对应变量的小扰动量。

2.3 PLL同步机制下的风机小扰动模型

当DFIG 系统采取PLL 作为并网控制方法时，与VSG 同步机制相同，也需考虑二者坐标系之间的偏差。进行线性化处理后可得PLL同步机制下的转换方程为：

2.4 小扰动稳定分析

2.4.1 小扰动模型特征值特性分析

通过求解式（9）中状态矩阵H，可分别得到PLL与VSG 同步机制下的DFIG 小扰动模型特征值λ=η+jω。其中：η为特征值的实部，表示阻尼；ω为特征值的虚部，表示振荡角频率。根据特征值可得该模式下的振荡频率和阻尼比等相关特性参数。振荡频率f及阻尼比ζ可通过式（13）计算得到。

当k=10 % 时，系统处于短路比（short circuit ratio，SCR）为5 的电网强度下，对2 种同步机制下的DFIG 系统进行小扰动分析，因纯实数特征根与系统的振荡模式无关，仅分析共轭特征值，特征值可见附录D 表D1 —D4。2 种同步机制下系统共轭特征值、振荡频率与阻尼比分别如表1、2所示。

表1 PLL同步机制下共轭特征值及其相关特性Table 1 Conjugate eigenvalues and their related characteristics under PLL synchronization mechanism

表2 VSG同步机制下共轭特征值及其相关特性Table 2 Conjugate eigenvalues and their related characteristics under VSG synchronization mechanism

参与因子pαi可通过式（14）计算得出，其表示在第i个特征值中第α个状态变量的参与程度。

式中：Vi、Ui分别为第i个特征值所对应的左、右特征向量；Vαi、Uαi分别为第i个特征值所对应的左、右特征向量中的第α个向量。

2 种同步机制下的共轭特征值主要参与因子（选取pki＞0.2的变量）分别如表3、4所示。

表3 PLL同步机制下共轭特征值及其主要参与因子Table 3 Conjugate eigenvalues and their main participation factors under PLL synchronization mechanism

表4 VSG同步机制下共轭特征值及其主要参与因子Table 4 Conjugate eigenvalues and their main participation factors under VSG synchronization mechanism

通过表1 —4可以得出如下结论。

1）PLL 同步机制下，振荡模式λ4，5、λ6，7所对应的振荡频率分别为44.34、50 Hz，其中λ4，5为次同步振荡模式；VSG 同步机制下，系统具有4 个振荡模式，振荡频率分布范围广，既有λ3，4对应的428.09 Hz 的高频振荡，也有λ9，10对应的3.71 Hz 的低频振荡；λ5，6所对应的振荡频率为48.07 Hz，为次同步振荡模式，相比PLL 同步机制，VSG 同步机制下的DFIG 系统引入了更多的振荡模式。

2）在PLL 同步机制下，PLL 输出角度θPLL与所串联的电容电压d轴分量ucd在λ4，5所对应的振荡模式中为主要参与因子，呈现强相关；在VSG 同步机制下，λ3，4所对应的振荡模式与虚拟同步控制环节中间变量z1强相关，λ5，6所对应的振荡模式所串联的电容电压q轴分量ucq也呈现强相关。各振荡模式除与上述变量强相关外，与定、转子电流分量均呈现强相关性，PLL 与VSG 同步机制在控制过程中均利用了定、转子电流，因此2 种同步机制均会对DFIG 系统的动态特性造成影响，改变系统的振荡模式。

2.4.2 电网强度改变时小扰动稳定分析

改变电网强度，在SCR 为2 的弱电网下，对PLL及VSG同步机制下DFIG系统进行小扰动分析，对其共轭特征值等相关参数进行分析有以下结果：在强电网下，系统各振荡模式阻尼比均为正，但当电网强度降低系统成为弱电网后，PLL 同步机制的DFIG 系统振荡模式λ4，5特征值实部为正，可见系统已经失稳；VSG 同步机制下系统各振荡模式特征值仍均为负，即仍保持稳定性，说明采用VSG 同步机制在弱电网下稳定性更高。

2.4.3 串补度改变时小扰动稳定分析

为分析弱电网下串补度对小扰动稳定的影响，在SCR 为2 时，改变VSG 同步机制下的DFIG 系统的串补度，其分析结果可见附录D 图D1。对次同步振荡模式λ5，6特征值实部变化趋势分析可得：弱电网下采用VSG同步机制虽然比PLL同步机制稳定性更好，但随着串补度的提高，特征值实部从负数变为正数，系统失稳，发生次同步振荡现象。

2.4.4Tj、D参数改变时小扰动稳定分析

VSG同步机制引入的Tj、D也会导致系统稳定性的改变，特征值分析结果分别见附录D 表D5、D6。在SCR为5，k=10 % 时，分别考虑Tj从0.65降低到0.1及增加到50、D从250 降低到10 及增加到1 000 这几种场景下系统的稳定性，分析各振荡模式特征值在以上场景下的变化趋势可得如下结论：

1）减小Tj，DFIG 系统各振荡模式特征值实部仍为负值，而Tj增加到50 后，系统振荡模式λ5，6特征值实部变为正值，系统不稳定，故Tj过大时系统失稳；

2）增加D，各振荡模式特征值仍为负值，但D减小到10 时，振荡模式λ9，10特征值实部存在正值，系统失稳，因此D过小会降低DFIG系统的稳定性。

3 基于StarSim-HIL 平台的有功特性实时仿真分析

离线软件对实际电网进行1 s 的动态仿真需要复杂的计算并消耗远多于1 s 的时间，计算效率低下，不能和实际电网及电力设备连接运行；实时仿真软件计算效率高，能与实际系统运行保持一致。因此本文仿真分析利用StarSim-HIL 半实物仿真平台进行μs 级小步长实时仿真。在StarSim-HIL 平台搭建图A1 所示的DFIG 并网系统，对不同同步机制下DFIG 的有功动态特性进行分析。StarSim-HIL 工作原理如附录E图E1所示。

3.1 动态特性比较仿真分析

改变风速，使风机所发出的有功功率从0.75 p.u.增加到1 p.u.，2 种控制方法下的有功功率动态特性如图2 所示，图中有功功率为标幺值，后同。由图可知：当风速变化时，在PLL 同步机制下，有功功率能够快速提升，但在VSG 同步机制下，有功变化较为缓慢。可见，由于PLL控制结构相对简单，能够快速实现有功功率的调节，但VSG 模拟同步机动态过程引入了虚拟惯量及阻尼系数，降低了一定的动态特性，调节速度较慢。

图2 风速改变时有功功率变化趋势Fig.2 Trend of active power change when wind speed changes

3.2 有功支撑能力对比仿真分析

将无穷大电网设置为火力发电机组，风电和火电机组系统总容量为100 MW。考虑在15 % 的风电渗透率下，在1 s 时改变所接入的负荷，2 种同步机制下风机有功功率变化如图3 所示。由图可知：当负荷改变时，PLL 同步机制下风机所发出有功功率并未发生变化；而VSG 同步机制下DFIG 系统能够对负荷变化进行响应，增发有功功率，对系统进行有功功率支撑，定子电流也随有功电流的增大而增大以响应负荷变化。由此采用VSG 同步机制控制策略能支撑系统的有功功率，并提高系统的有功支撑能力。

图3 负荷变动时有功功率变化Fig.3 Active power change when load fluctuates

4 基于StarSim-HIL平台的DFIG 系统小扰动特性实时仿真分析

为验证上述小扰动特征值分析方法及结果的合理性，在StarSim-HIL平台进行了实时仿真验证。

4.1 电网强度变化时的仿真分析

当低串补度k=10 % 时，分别改变PLL 和VSG 2种同步机制下DFIG 系统电网强度，1 s 时电网SCR由5 变为2，PLL 同步机制下的DFIG 定子电流（标幺值）仿真结果如图4所示。

图4 PLL同步机制下的定子电流波形Fig.4 Stator current waveforms under PLL synchronization mechanism

取2种同步机制下的定子电流在0.9 s与1.3 s时的总谐波畸变率（total harmonic distortion，THD）进行对比，并对失稳时定子电流进行快速傅里叶变换（fast Fourier transform，FFT）谐波分析，其结果可见附录E 图E2 —E6。由图可知：在低串补度下，当电网强度由强变弱时，PLL 同步机制下的DFIG 系统从稳定状态变为不稳定状态，其定子电流变化趋势反映了这一特点；VSG 同步机制下的DFIG 系统定子电流虽有明显变化的趋势，但是其仍处于稳定状态；通过对比二者定子电流的THD 变化趋势，也可发现PLL 同步机制下DFIG 系统在弱电网下定子电流的THD 变化大，畸变明显。由失稳时的定子电流FFT结果也可看出：失稳时其振荡频率主要集中在40 Hz附近，属于次同步振荡范围。

通过以上仿真并结合特征值计算结果可看出，电网强度由强变弱，导致DFIG 系统电流出现变化，λ4，5这一振荡模式与isq及θPLL呈现强相关性，故在PLL 同步机制下该振荡模式阻尼比由负变正，出现失稳现象。仿真分析与特征值分析一致，可证明VSG 同步机制能提高DFIG 系统在弱电网下的稳定性。

4.2 串补度变化时仿真分析

当DFIG 系统运行在弱电网下，即SCR 为2 时，改变VSG同步机制下的DFIG系统串补度，当k=20 %时，其有功功率发生次同步振荡的仿真结果见图5。

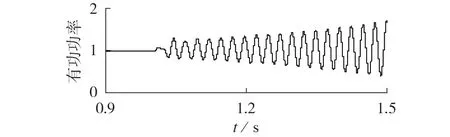
图5 当k = 20 %时VSG同步机制下的系统次同步振荡波形Fig.5 System subsynchronous oscillation waveforms under VSG synchronization mechanism when k = 20 %

发生上述次同步振荡情况下，对定子电流进行FFT 分析，VSG 同步机制下的DFIG 系统在弱电网下时，串补度达到20 % 就会失稳，发生振荡现象，通过FFT 分析可知，其振荡频率主要在40 Hz 附近，为次同步振荡。

以上仿真结果与前述特征值分析结果一致，从特征值计算及仿真结果可看出：随着串补度的提高，输电线路电容值增加，与电感发生串联谐振现象；λ5，6这一振荡模式与ucq呈现强相关关系，电容值的提高也会导致系统出现失稳现象。由此可见，利用VSG 同步机制并网同步，在弱电网下能提高一定的稳定性，但随着串补度的提高，也会发生失稳现象。

4.3 Tj、D变化时的仿真分析

在SCR 为5、k=10 %、D=250 情况下，1 s 时分别将Tj减小到0.1 和增加到50，有功功率及THD 分析结果分别如图6 及附录E 图E7 所示。由图可知：当Tj减小时，系统仍然保持稳定；但Tj增大到一定数值后，THD达到正常运行时的数十倍，说明此时定子电流畸变很大，有功功率变化趋势也说明系统已失稳。

图6 改变虚拟惯量时有功功率变化趋势Fig.6 Trend of active power change when virtual inertia changes

VSG 同步机制模拟同步机的同步过程，当Tj增加到一定程度后，DFIG 系统的总惯量随之增大，致使系统超调量增加，系统稳定裕度下降，导致系统失稳，从图6 可看出：在虚拟惯量过高时，有功功率在1 s 到1.5 s 之间出现明显超调后，DFIG 系统最终走向失稳；而在虚拟惯量较低时，系统最终仍能保持稳定。特征值结果也表明系统从稳定走向失稳，与仿真分析结果一致。

在SCR 为5、k=10 %、Tj= 0.65 情况下，1 s 时分别将D减小到10 和增加到1 000，其有功功率及THD分析结果分别如图7 及附录E 图E8 所示。由图可知：当D增大时，系统仍然保持稳定；但D减小到一定数值后，THD达到正常运行时的数十倍，说明此时定子电流畸变很大，有功功率变化趋势也说明系统已失稳。

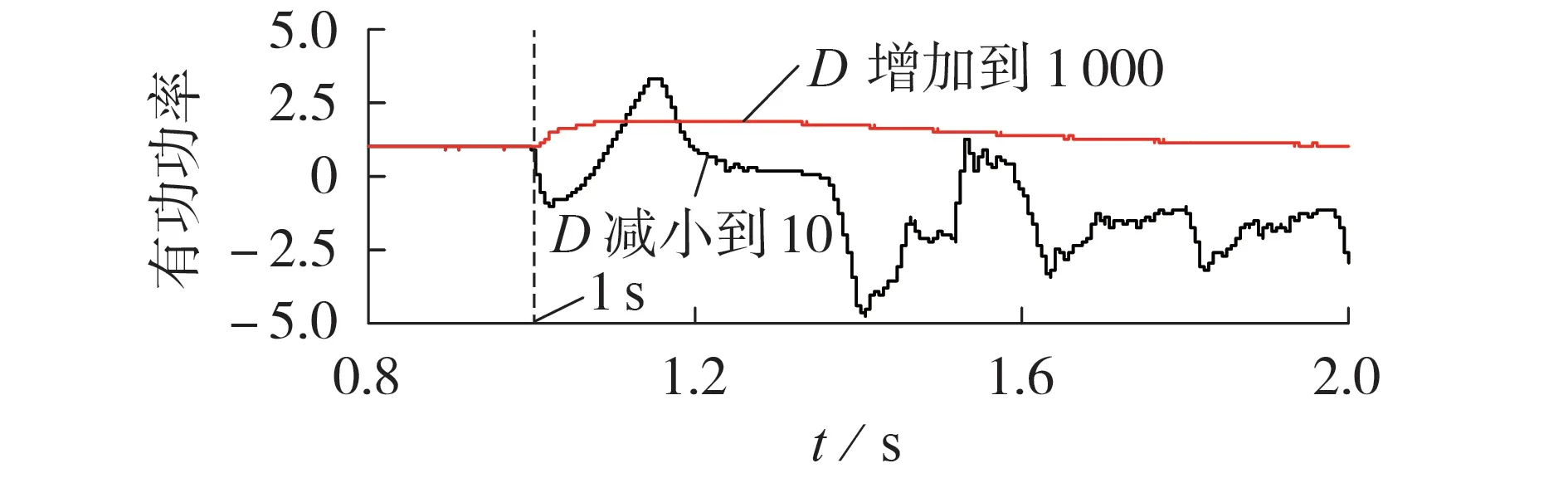
图7 改变阻尼系数时有功功率变化趋势Fig.7 Trend of active power change when damping coefficient changes

阻尼系数能够在电力系统发生变化时起到阻尼作用，抑制系统振荡的发生。当DFIG系统配置参数不合适时，系统出现阻尼不足会导致系统失稳等现象发生。因此在VSG 同步机制下，所引入的阻尼系数需达到一定数值，当阻尼系数过小时，系统会出现不稳定现象。特征值所对应的振荡模式实部随着阻尼系数减小由负转正，有功功率无法正常输出，均说明了阻尼系数不可过小。

5 结论

本文在考虑同步机制的基础上，分别搭建了基于PLL 与VSG 2 种同步机制下DFIG 系统的小扰动模型，利用了特征值分析法对系统的小扰动稳定性进行分析，最后在StarSim-HIL 平台中，分别从有功动态特性及小扰动稳定性2 种角度对二者控制下的系统进行了半实物仿真，并对相关结果进行了解释分析，最终得出的结论如下：

1）PLL 同步机制下DFIG 系统动态特性好，响应速度快，VSG同步机制模拟同步机的工作特性，在负荷变动时对系统进行一定有功支撑，但牺牲了部分动态性能；

2）在小扰动分析中，相比于PLL 同步机制，VSG同步机制引入了更多的振荡模式，且振荡模式所对应的振荡频率分布更广；

3）VSG 同步机制下的DFIG 系统在弱电网中具有更好的稳定性，但随着串补度的提高，也会产生次同步振荡，导致失稳现象发生；

4）VSG 同步机制下的DFIG 系统，引入了虚拟惯量和阻尼系数，虚拟惯量过大及阻尼系数过小都会引起系统的失稳。

综上，在有功动态特性方面，当系统处于有大量火电机组支撑的强电网场景下，采用PLL 同步机制能提升电力系统的动态特性，但在弱电网的场景下，采用VSG 同步机制能对电力系统进行一定的有功支撑，提高系统的稳定性；在小扰动稳定性方面，VSG 同步机制因引入虚拟惯量和阻尼系数，能够提高DFIG 系统小扰动稳定性，但在串补度过高时，需考虑抑制措施防止次同步振荡的失稳现象发生。

附录见本刊网络版（http：//www.epae.cn）。