基于改进灰狼算法的机械臂力矩最优轨迹研究

李克讷，贺之祥，唐春怡，胡旭初

（1.广西科技大学 自动化学院，广西柳州，545616；2.广西柳州特种变压器有限责任公司，广西柳州，545006）

0 引言

轨迹规划是机械臂运动控制的基础，其性能对工业机器人工作效率和能量消耗具有重大影响[1]。根据应用场景与生产需求不同，轨迹规划的目标可被分为时间最优、力矩最优等。其中，机械臂关节驱动力矩大小与其能耗及结构性能密切相关，在保证机械臂可以完成指定任务的同时，减少机械臂的关节驱动力矩，不但可以降低使用能耗，而且可以避免机械臂驱动力矩超限，延长使用寿命[2]。

力矩最优轨迹规划是指在满足角度、角速度、角加速度等各种约束条件下，确定一条以机器人关节驱动力矩均值和最优为目标的运动轨迹。程亚等通过双种群布谷鸟算法优化关节力矩能耗，有效降低机械臂关节力矩总能耗[3]。ZHAO通过结合双种群布谷鸟算法与五次多项式插值法优化机械臂关节驱动力矩，规划出关节力矩和最优轨迹[4]。目前已有粒子群算法、布谷鸟算法和遗传算法等优化算法被用于机械臂力矩优化，虽然这些优化算法使得机械臂力矩最优轨迹规划效果得到改善，但是仍然存在易陷入局部最优解、收敛速度慢等问题。

本文提出一种基于改进灰狼算法的关节力矩优化方法，实现了对机械臂的力矩最优轨迹规划，并将所提算法与PSO、GWO 算法进行对比实验，可以看出改进灰狼算法收敛速度更快，对机械臂力矩优化效果更好。

1 问题描述

■1.1 定义目标函数

在目标函数的选取上，考虑机械臂关节力矩均值和最小为优化目标。定义其目标函数为：

式中，θmax为角度最大值，为角速度最大值，为角加速度最大值。

■1.2 五次多项式插值法构造关节轨迹

五次多项式插值法不仅可以解决三次多项式插值法中加速度突变问题，还能够适当减少运动过程中的冲击震荡。因此，采用五次多项式插值法对机械臂进行轨迹规划[5]。

对于六自由度机械臂而言，包含n个路径点的轨迹可以表示为θij(i= 1,2,… ,n)。设{t1,t2,… ,tn}是与关节j的路径节点对应的时间序列。定义为第i条轨迹中关节j的角度、角速度与角加速度。则五次多项式定义为：

式中，t为时间，aji,(i= 0,1,… ,5)为待定系数。

根据两个相邻路径点的角速度和角加速度的连续性条件，五次多项式各项系数可以表示为：

式中，tf=ti+1-ti,(i= 0,1,… ,n- 1)表示两个路径点之间的时间间隔。如果tf已知，是待优化的变量，θj(t),(t)和(t)可以由式(3)唯一确定。

2 改进灰狼优化算法

■2.1 标准灰狼优化算法

灰狼优化算法(grew wolf oplimizer, GWO)[6]借鉴了灰狼种群严格的社会分工以及分工协作的捕食策略，通过不停迭代更新种群中灰狼位置从而实现最优解的求取。该算法的基本特性如下：

（1）社会等级分层

灰狼种群的社会等级划分如图1 所示，狼群根据个体适应度进行排序被划分为α，β，δ和ω狼，前三个表现最好的设为α，β，δ狼，其余的候选解则被认为是ω狼。在GWO 算法中，α，β，δ狼负责指挥狼群搜索，ω狼则跟随它们。

图1 狼群的社会等级

（2）包围猎物

灰狼在追踪猎物过程中，逐渐逼近猎物形成包围圈，其数学模型如下：

式中，t为当前迭代次数，为向量各分量取绝对值，X(t)为t次迭代后灰狼位置，Xp为t次迭代后猎物的位置，D为灰狼与猎物的距离， ( )Xt+1 为t+1 次迭代后灰狼位置，A 和C 为系数向量，定义为：

式中，1r 和2r 是[0,1]之间的随机向量，a为收敛因子，定义为：

式中，tmax为最大迭代次数，a随迭代次数的增加由2线性降低到0.

（3）狩猎

在狩猎过程中，假设α、β 和δ 狼作为每次迭代适应度最好的前3 头狼。其他灰狼个体在α、β 和δ 狼的指导下更新自己的位置，狼群逐渐向猎物位置靠近，其数学模型如下：

式中，Xα、Xβ和Xδ分别表示为α、β和δ狼在当前迭代次数时的位置，X(t+)1 表示ω狼在t次迭代后的位置，1A、2A和3A的计算相似于A，1C、C2和C3的计算相似于C。

■2.2 改进灰狼优化算法

式中，t 为当前的迭代次数， tmax为最大迭代次数，n为调节系数，用以调节权重的大小。调节系数取不同权重值时收敛因子变化如图2 所示。

由图可见，在算法迭代前期，所提出的非线性收敛因子a可以保持较大步长以提高算法前期的全局搜索能力。算法迭代后期，算法逐渐收敛，余弦型非线性收敛因子相应减小，小步长有利于增强算法的局部开发能力。并且当0.9≤n≤1.5，可以明显改善算法的性能，当n=1.1 时，算法的全局和局部搜索能力平衡效果最好，因此本文取n=1.1 。

■2.3 IGWO 算法步骤

IGWO 的具体实现步骤如下：

Step1：初始化改进灰狼算法基本参数，设置灰狼种群规模N，空间维度dim，搜索空间的上下限ub 和lb，最大迭代次数 tmax；

Step2：初始化灰狼位置，生成初始种群；

Step3：计算各个个体的适应度值{fi,i=1,2,3,…,N}，将适应度值从小到大按顺序排列，将适应度值前三所对应的个体确定为α、β、δ，其对应的位置信息分别为Xα、Xβ和Xδ。

Step4：利用式计算非线性控制参数a，式和分别更新A 以及C 值，式-更新狼群位置，通过更新猎物位置。

Step5：跳至Step3 直到达到终止条件，即到达最大迭代次数tmax。

Step6：输出最优解α 狼的位置。

3 仿真分析

■3.1 仿真条件

本文以六自由度工业机械臂PUMA560 为研究对象进行数值仿真，机械臂初始角度为θ= [90°,0°, -9 0°,0°,0°,0°]，根据改进D-H 坐标系法则建立对应坐标系如图3 所示，该方法建模简单，具有通用性，被广泛用于机器人的运动学建模。表1 为PUMA560 机械臂D-H 参数表。

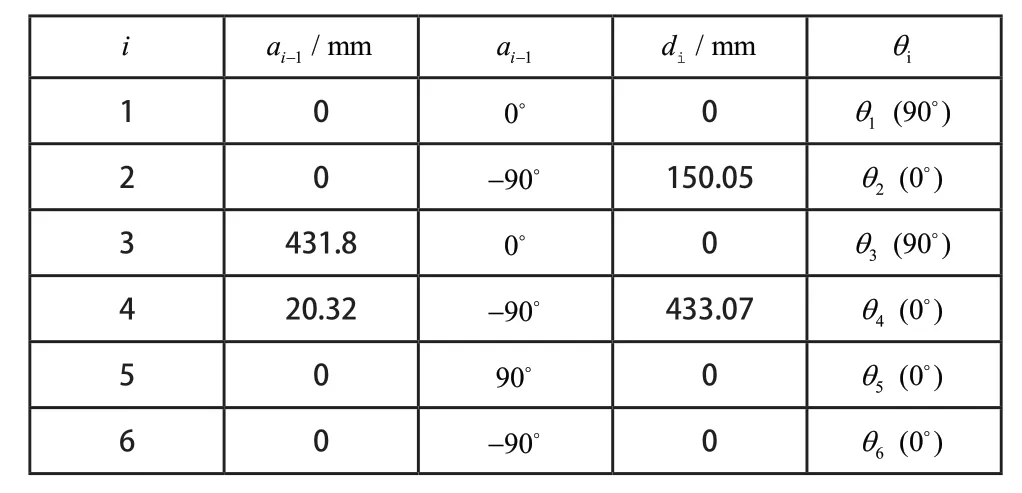
表1 D-H参数表

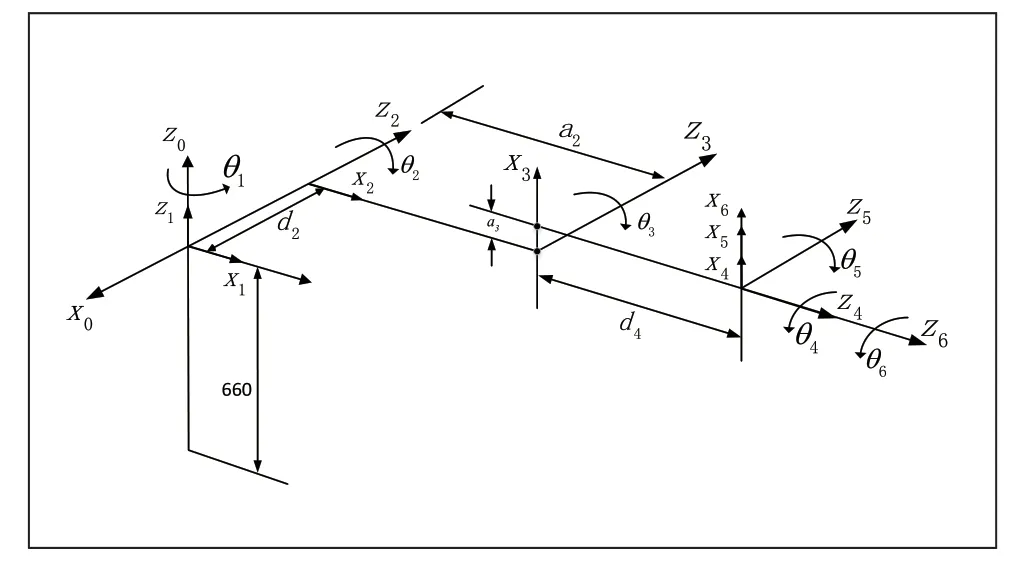
图3 PUMA560 坐标系建立

表2 为机械臂质量特性参数表，可得到机械臂系统的惯性质量参数以及质心坐标向量参数。本文使用拉格朗日法结合表2 求各关节力矩的变化值，作用在机械臂关节i 的驱动力矩：

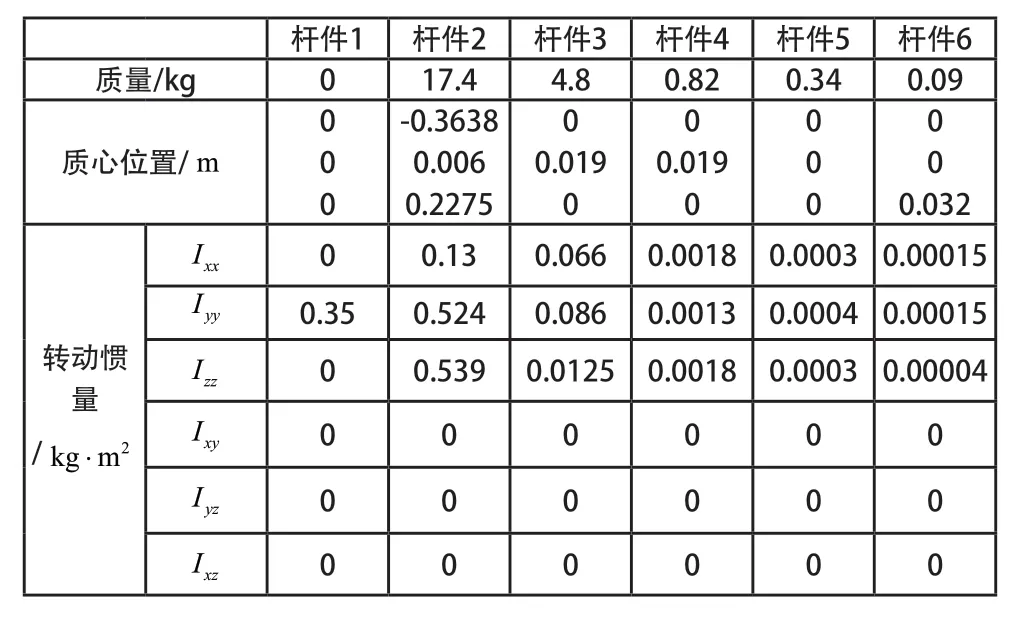
表2 机械臂质量特性参数表

式中，第一项为角加速度惯量项，第二项为科里奥利力和向心力项，第三项为驱动器惯量项，第四项为重力项。

此外，应约束机械臂运行过程中的关节角度、角速度和角加速度，以确保其平稳运行，不会受到冲击和抖动。PUMA560 机械臂运行过程中关节角度、速度及加速度约束条件如表3 所示 。

表3 机械臂关节约束条件

■3.2 仿真实验

为了验证算法的有效性，本文使用MATLAB 中的Robotics Toolbox 工具箱对PUMA560 机械臂进行建模和仿真。在实验中，给定4 个路径点，路径点信息如表4所示。本实验设种群规模为50，迭代次数为100。将起点与终点处的角速度、角加速度指定为0，每两个路径点之间的运行时间为2 秒，以中间路径点关节速度作为待优化变量。

表4 路径点序列

为验证本文所选取的系数权重n=1.1 的合理性，本文对GWO 和IGWO 的n=1.1 、0.9、1.5 四种情况分别测试，结果如图4所示。从图4可以看出，当系数权重选取为n=1.1 时，优化后的关节力矩均值和明显小于其他情况，结果更优。

图4 不同系数权重n 优化结果

将IGWO 优化后的关节力矩均值和与PSO 和GWO 做比较，可得如图5 所示的机械臂关节力矩均值和最优曲线，三种不同算法对各关节力矩均值和最优解的优化都有明显效果，但IGWO 算法比PSO 算法和GWO 算法有更好的收敛精度，并且陷入局部最优时能快速跳出。

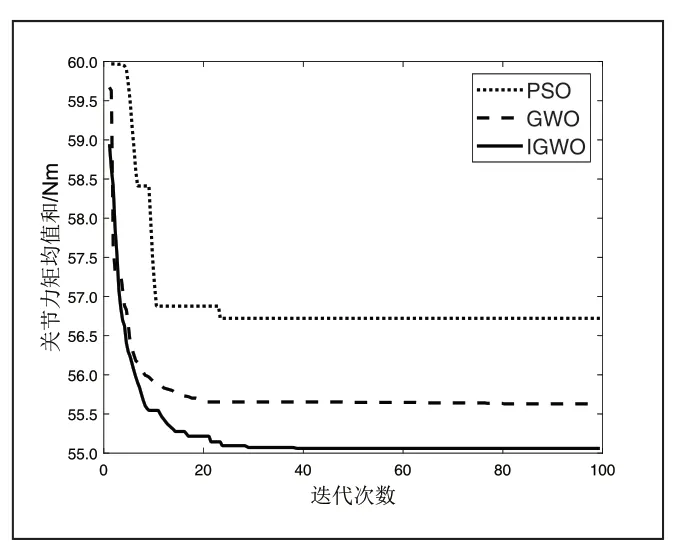
图5 PSO，GWO 和IGWO 算法优化过程

通过PSO、GWO 和IGWO 算法获得的最优力矩均值和以及实现收敛所需的时间如表5 所示。从表5 可以看出，IGWO 算法优化后得到的结果最好，同时IGWO 算法所需的收敛时间更少。

表5 PSO，GWO和IGWO算法优化后最小力矩均值和以及收敛时间

优化后关节角度、角速度、角加速度和最优力矩曲线图如图6 所示，从图(a)- (c)中可以看出各关节角度、角速度和角加速度曲线平滑连续，说明机械臂各个关节能够在路径点之间连续地完成所设定的轨迹任务；图6(d)为最优关节驱动力矩变化曲线，求解得到的关节驱动力矩曲线光滑连续，符合机械臂的设计要求，方便后续在工程实际中应用。

图6 关节角度、角速度、角加速度和最优力矩曲线图

4 结论

本文提出一种改进灰狼算法对六自由度串联机械臂关节力矩优化方法。利用余弦型非线性收敛因子改进GWO 算法使其可以快速跳出局部最优解，提高全局搜索能力，同时加快了算法的收敛速度。仿真结果表明：相比标准GWO 算法与PSO 算法，IGWO 算法所需收敛时间更短，且优化后的机械臂力矩均值和更小，结合IGWO 算法与五次多项式插值法可以规划出一条关节力矩均值和最优的运动轨迹；同时该方法仿真得到的机械臂运行轨迹角度和角速度曲线平滑，角加速度曲线连续，可以满足机械臂运动学约束条件。仿真结果说明了IGWO 算法可以应用到机械臂力矩优化中，且能够实现机械臂力矩最优轨迹规划。