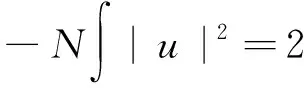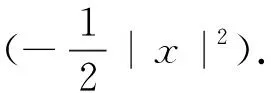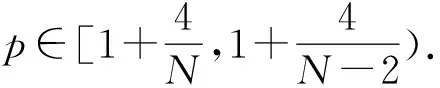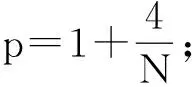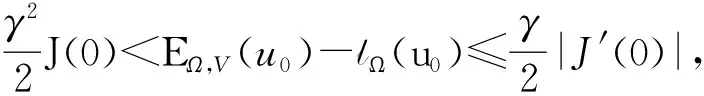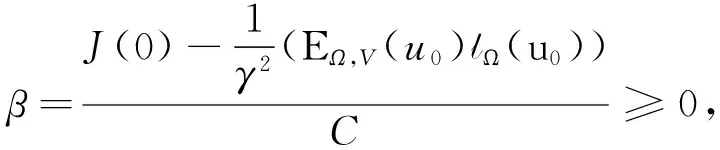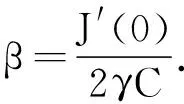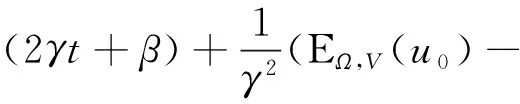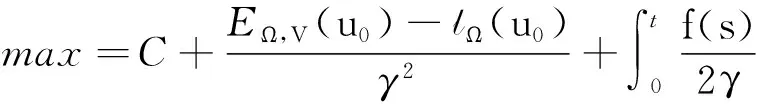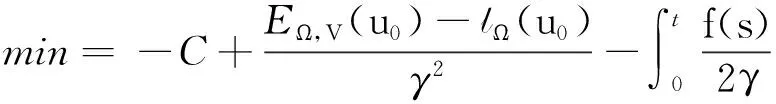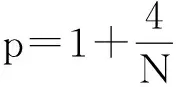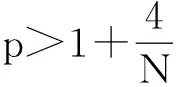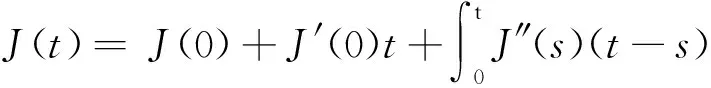一类带旋转的Gross-Pitaevskii方程
2023-09-10陈咨宇
陈咨宇, 张 健
(电子科技大学 数学科学学院, 四川 成都 611731)
1 研究背景
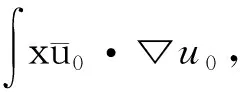
本文考虑带旋转的Gross-Pitaevskii方程在部分限制下的柯西问题:
iu
LΩu=0, t≥0, x∈RN,
(1)
u(0,x)=u0(x),
(2)
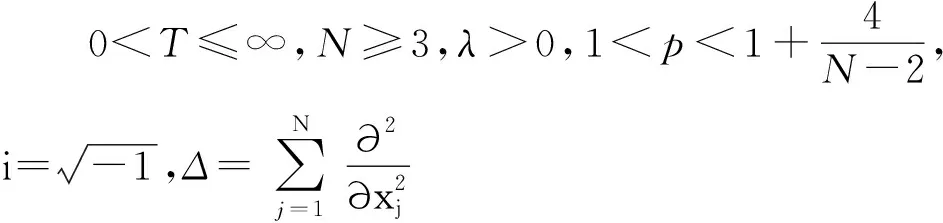
Lz=i(x2∂x1-x1∂x2),
A=Ω(-x2,x1,0,…,0)∈RN.
刻画玻色-爱因斯坦凝聚(BEC)的数学模型通常被称为Gross-Pitaevskii方程(简称G-P方程),最早是由Gross[1]和Pitaevskii[2]提出.针对稀薄原子气体中BEC的研究,值得注意的超流体特征是量化涡旋[3].目前,从BEC基态产生量化涡旋的最常用的方法之一是:在控制原子的磁陷阱上施加以角速度旋转的激光束,以产生谐波各项异性的势[4-5].根据平均场理论,当温度T低于临界温度Tc时,在旋转框架下的BEC能够由宏观的波函数u(t,x)所刻画,它的演化由一个带角动量旋转项的G-P方程控制[6-8].在最新的偶极BEC等宏观量子现象研究中,外势被限制在部分方向上.类似地,本文利用在部分限制下带旋转的G-P方程模拟此模型.
对非线性薛定谔方程的研究,引起了众多数学家的关注.回顾经典非线性薛定谔方程
iut+Δu+|u|p-1u=0,t≥0,x∈RN,
(3)
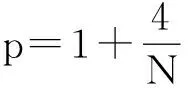
ΔQ-Q+|Q|
Weinstein[13]和Zhang[14]分别得到在L2-临界与L2-超临界非线性项爆破解与整体解存在的最佳门槛,证明了此柯西问题爆破解存在的最佳充分条件是
‖u0‖L2<‖Q‖L2.
对于带调和势的非线性薛定谔方程
iut+Δu-|x|2u+|u|p-1u=0,
t≥0, x∈RN,
(4)
Oh[15]和Cazenave[16]在相应的能量空间中建立了柯西问题(2)和(4)的局部适定性,Tsurumi等[17]和Zhang[18-19]研究了其爆破解的存在性,Zhang[19]得到了其爆破解整体存在的最佳充分条件.
对于带部分调和势的非线性薛定谔方程
iu
t≥0, x∈RN, 2≤k≤N-1,
(5)
Antonelli等[20]在相应的能量空间内建立了柯西问题(2)和(5)的局部适定性以及散射性质;当外势限制在部分方向时,Ohta[21]研究了此方程驻波解的不稳定性.
Basharat等[22]已经对如下在调和限制下带旋转的非线性薛定谔方程做出了研究
iu
t≥0, x∈RN.
(6)
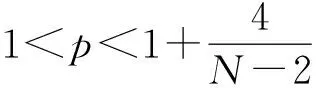
基于以上的研究,通过比较方程(1)和(6),发现由于限制的作用,使得方程的平移不变性、旋转不变性等不变性缺失,从而导致尺度变换等重要技术的失效,引起理论研究上的新困难.初步研究显示,带限制的非线性薛定谔方程和带部分限制的2种情形有显著的差异.典型的是在调和限制有空间对称,而在部分调和限制情形中空间对称性丢失,从而导致在临界质量爆破解的研究上必须寻求新的方法和路径.
本文主要研究柯西问题(1)和(2)的爆破解存在的充分条件.主要工作如下:通过利用文献[16]的方法建立了柯西问题(1)和(2)在相应的能量空间的局部适定性(也可见文献[20,31]).根据文献[18]的启示,选择不带任何势的经典非线性薛定谔方程的基态解刻画柯西问题(1)和(2)的爆破解,进而利用Virial恒等式和Hamilton守恒律可得到柯西问题(1)和(2)的爆破解存在的充分条件.
2 预备知识
本节将给出一些准备知识.定义能量空间
H={u∈H1(Rdx<∞,
2≤k≤N-1},
其中
H1(RN)={u:u∈L2(RN),▽u∈L2(RN)}.
显然H是一个Hilbert空间,赋予其内积为
〈φ,ψ〉dx,
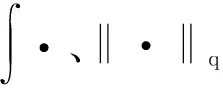
为了计算简便,给出以下的命题.
命题 2.11) 由定义可知A=Ω(-x2,x1,0,…,0),则x·A=0.
2) 角动量算子Lz=i(x2∂x1-x1∂x2)是自伴算子,且满足Lz(|x|2)=0.
3) 定义角动量:lΩ(u)=〈LΩu,u〉.
〈L
角动量lΩ(u)是实的.这里内积定义为
证明结论1)和2)显然.现在仅证明结论3).
取其共轭,利用分部积分法,有
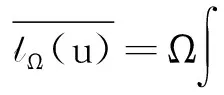
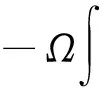
根据文献[16,20,31]给出方程(1)的局部适定性.
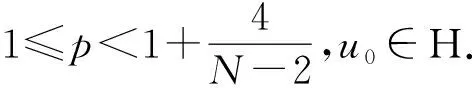
1) 设u0∈H,则得到柯西问题(1)和(2)一定存在唯一解u(t,x)∈C([0,T*);H),0 2) 对任意时间t∈[0,T*),u(t,x)满足以下的守恒律: 质量守恒 (7) 能量守恒 E (8) 角动量守恒 lΩ(u)=〈L (9) 为了阅读方便,我们证明守恒律. 其中lΩ(u)=〈LΩu,u〉是实的,则令 可证得方程(1)质量守恒. 其中 (x2∂x1-x1∂x2)u 因此 则令 E 可证得方程(1)的能量守恒. Re(I1-I2+2I3). 注意有[Δ,Lz]=0,因此由I可知ReI1=0.对于I2,有 I -γ 对I2取实部,有ReI2=0.由于x2∂x1-x1∂x2是反对称的,对于I3有 I 对I3取实部,有 Re(I3)=-pRe(I3)⟹Re(I3)=0. 结合I1、I2和I3的结果,得到 (10) 因此方程(1)的角动量守恒. 命题 2.3(Virial等式) 设u0∈H,且|x|u0∈L2.如果对应的柯西问题(1)和(2)的解u(t,x)其最大存在区间为[0,T*),则对任意的t∈[0,T*),u(t,x)∈C([0,T*),H).记 则 (11) 2γ 4EΩ,V-4γ (12) 本节将利用Virial等式及守恒律讨论柯西问题(1)和(2)爆破解存在的充分条件. 由文献[13],首先给出如下的不等式. 引理 3.1设 u∈∑={u∈H 则 (13) 证明由等式 和Cauchy-Schwarz不等式可得到上述不等式. 这里 则存在0 证明由方程(7)~(9),证明可分为2种情形. J″(t)+4γ 4EΩ,V(u0)-4lΩ(u0). (14) 因此,得 J″(t)+4γ2J(t)= 4EΩ,V(u0)-4lΩ(u0)+4γ 解这个常微分方程,可得到 lΩ(uds= (15) 这里 f(t)=4γ C>0,β∈(0,π),且 C (16) 条件1)成立时,有 则由C2的表达式可知,不论EΩ,V(u0)-lΩ(u0)是正还是负,始终有如下关系式成立 (17) 因此,可知 lΩ(uds, (18) 此时对J(t)有 必定存在T使得 由引理3.1中的(13)式以及质量守恒可知,存在某个常数c0,使得 ‖▽u‖ 因此,此时柯西问题(1)和(2)的解u(t,x)在有限时间T*<∞爆破 则(17)式依然成立.后续证明和以上的步骤相同,必定存在有限时间T*使得 J″(t)≤4(EΩ,V(u0)-lΩ(u0)). 根据经典的分析恒等式 (19) 有 0≤J(t)≤ J(0)+J′(0)t+2(EΩ,V(u0)-lΩ(u0))t2. 若u0满足条件3)、4)或5),则必定存在有限时间T*使得 注 3.1若V=γ2|x|2|u|2是调和势[22],则定理3.1中的条件1)等价于 EΩ,V(u (20) 即当E0,0(u0)≤0时,柯西问题(2)和(6)的解在T*处爆破.然而,当 V=γ 是部分调和势时,上述条件就不再成立.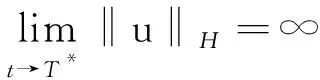

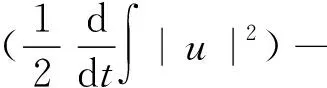
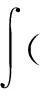

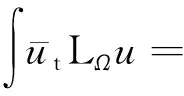

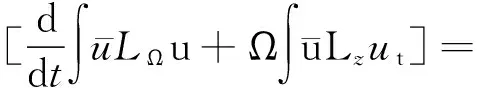
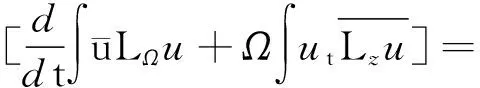

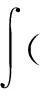


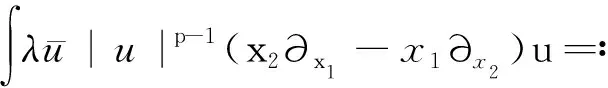

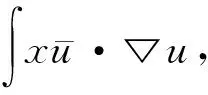
3 带旋转的G-P方程爆破解的充分条件