含临界指数的多重奇异拟线性椭圆系统正解的存在性
2023-09-10杜刚
杜 刚
(喀什大学 数学与统计学院, 新疆 喀什 844007)
本文研究下述含临界指数的多重奇异拟线性椭圆系统
正解的存在性,其中N≥3,Ω是RN中一有光滑边界的有界区域,λ,η,δ>0,
Δpu=-div(|▽u|p-2▽u),
α>1,β>1,α+β>p,α+β=p*.
近年来,含临界指数的奇异拟线性椭圆系统一直受到人们的关注[1-6].其中:文献[1-3]利用变分方法和分析技巧,研究了含多个奇异点和临界指标的半线性椭圆系统的正解的存在性;文献[4]利用Nehari流形得到系统
多解的存在性;文献[5-6]利用变分方法和集中紧原理,得到含临界指数的p-Laplacen奇异拟线性椭圆系统解的存在性.对于含临界指数的多重奇异p-Laplacen系统解的存在性的研究目前结果很少,本文将讨论含有Hardy奇异项和强弱耦合项的p-Laplacen系统正解的存在性.
解决问题(1)的主要困难在2个方面:一是含有Hardy奇异项和Sobolev临界指数;二是强耦合项|u|α-2|v|βu、|u|α|v|β-2v与弱耦合项|u|p*-2u、|v|p*-2v相互作用,从而使得系统变得更为复杂且泛函不满足(PS)c条件.本文主要是通过应用Lions集中紧原理和山路引理,解决了上述问题,得到了在一定条件下此类拟线性椭圆系统正解的存在性.
1 预备知识及主要引理

‖(u,v)‖pW=‖u‖p+‖v‖p.
由Young不等式,可定义最佳常数
Aμi=
Aμi在RN的达到函数是
Vξiμi,ε=ε
其中
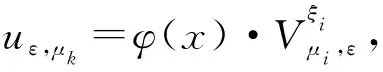
φ(x)=1, |x|≤R;φ(x)=0, |x|>R.
由文献[7]有如下估计
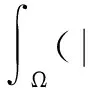
(Aμi)
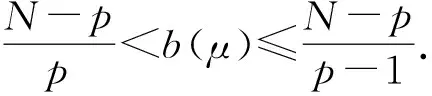
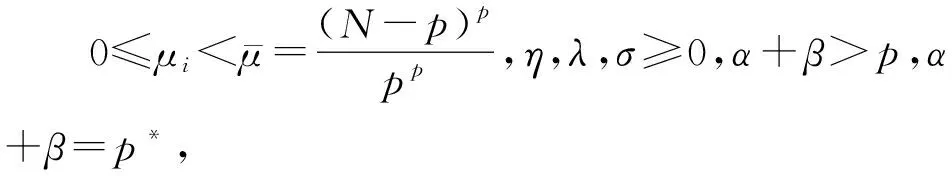
Aη,λ,σ(μi)=
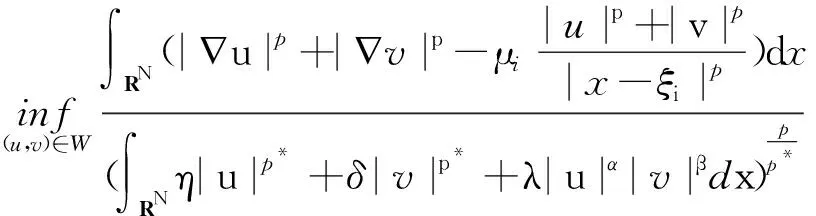
(2)

(3)


A
(4)
则泛函J满足(PS)c条件.
证明设{(un,vn)}⊂W,满足J(un,vn)→c (un,v在W中, (un,v在Lp(Ω,|x-ξi|-p)× Lp(Ω,|x-ξi|-p)中, (un,v在Lp*(Ω)×Lp*(Ω)中, |∇un|p+|∇vn|∇u|p+ |∇v| λp|un|α|vn|β+η|un|p*+δ|vn| δ|v| 由Sobolev不等式,有 Aη,λ,σ(μ Aη,λ,σ(μ (5) δ|vn|p*)φj(x)dx], 其中 δ|vn|p*)φj(x)dx)= δ|v|p*)φ 所以 再由Sobolev不等式 可得 或 φi(x)=1,x∈B(ξi,ε), φi(x)=0,x∈B(ξi,2ε)c δ|vn|p*)φi(x)dx)= δ|v|p*)φ 所以 (6) 由(5)和(6)式可得 Aη,λ,σ(μ 所以 或 另一方面 δ|vn|p*)dx= δ|v| A (un,vn)→(u,v). 为进一步研究Hardy-Sobolev常数Aη,λ,σ(μi),在引理1.1条件H1满足下,设 f fη,λ,σ(τ 其中τmin>0是fη,λ,σ(τ)的极小值点. 引理 1.2设条件H1满足,则: (i)Aη,λ,σ(μi)=fη,λ,σ(τmin); 证明类似于文献[10]. 引理 1.3设条件H1满足,则对∀t≥0,有 证明定义函数 g(t)=J(tuε,μk,t(τminuε,μk)), 易见 在t充分靠近0时,g(t)>0,因而存在tε>0,使得 g′(tε)=0, δτ 注意 所以 g(t 即∀t≥0,有 定理 2.1假设条件H1成立,则楕圆系统(1)至少有一个正解. 证明设 Τ={h∈C([0,1],W)|h(0)=0,J(h(1))<0}, 由Young不等式和Hardy-Sobolev不等式,有 J(u,v)≥c‖(u,v)‖pW-c′‖(u,v)‖p*W. 由上式可得,存在充分小的常数ρ>0,有 另外,当 t→+∞,J(tu,tv)→-∞, 因而存在t0>0,使得 ‖(t0u,t0v)‖>ρ, 且 J(t0u,t0v)<0. 由山路引理[11]可得,存在{(un,vn)}⊂W,有 J(un,vn)→c,J′(un,vn)→0. 由引理1.3可得 由引理1.1知{(un,vn)}存在子列,仍记为{(un,vn)},在W上(un,vn)强收敛于(u,v),且 J(u,v)=c,J′(u,v)=0, 即问题有解. 设 u-=min{u,0},v-=min{v,0}, 同理可得 〈J′(u,v),(u-,v-)〉=0, 从而u≥0,v≥0,再根据极大值原理可得(u,v)是问题(1)的正解.

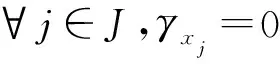
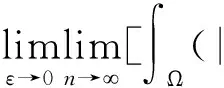
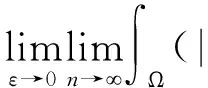
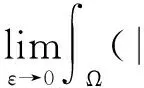
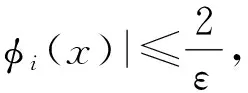
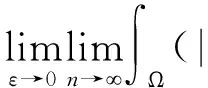
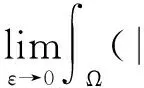

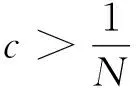
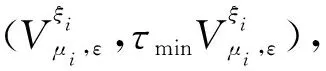
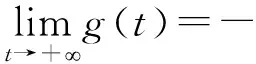
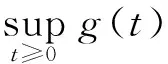

2 定理的证明
